基于改进A*算法的最优路径搜索

朱云虹，袁 一

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003；2.南京大学 地理与海洋科学学院，江苏 南京 210093)

0 引 言

近年来，随着地图应用和导航技术的迅速发展，在覆盖GPS的移动设备上(例如手机和汽车)利用地图应用程序来搜索目的地路线的行为已经越来越普遍。当输入初始地点和目的地后，几秒钟最短路线将显示在移动设备上。目前地图应用程序通过路网进行搜索，通常有两个重要功能，分别是距离查询和路径查询。距离查询是查询地图中两点之间的最短距离，路径查询是查询地图中两点之间具有最短距离的路径。

最短路径[1]作为路网中的焦点问题之一，目前已在计算机通信、运筹学以及地理信息系统等领域得到广泛应用，主要涉及智能交通[2]、地理信息系统[3]、路径规划[4]、计算机网络[5]等。从20世纪50年代起，研究者们就对最短路径问题展开了深入探索，研究最短路径问题的目标是在网络中搜索两个节点之间最有效的最短路径。一系列经典算法的诞生奠定了最短路径算法的基础，主要包括：计算一个节点到全部任意节点之间最短路径的Dijkstra算法[6]，计算任意对节点间最短路径的Floyd算法[7]，以及智能A*算法[8]。

大多数路网的研究通常都集中在如何减少最短路径查询的计算时间上面。例如，基于覆盖的算法[9]减少了查询的预处理时间，比普通A*算法和Dijkstra算法的查询速度快10倍；一种称为动态层次结构的算法(AH)通过缩小理论与实践之间差距的指标体系来优化路网上的最短路径和距离查询时间[10]。但是上述算法仅仅能够优化查询的计算时间，并不能改善最短路径实际消耗的行程时间。

RoadRank算法是在城市道路网中计算每个路段的影响分数算法，并能根据总体分数进行排序，通过在每个时间点提供最新的交通数据，不断随时间增量更新影响分数。RoadRank算法可用作动态城市道路网络的交通拥堵和影响估计[11]，给出了每个路段的影响分数。该算法考虑到了拥挤，但忽略了每个节点上的交通灯。

交通灯是城市交通网络的重要组成部分[12]，随着城市流量的增加，人们因为等待交通灯消耗的时间越来越长。目前，部分大城市的交通堵塞问题十分严峻，已成为社会待解决的一大难题，极大影响了群众的正常出行。因此，交通灯对最短路径的影响不可忽视。地图应用程序提供的最短路线并不一定是想要的路线，在实际路网中用户消耗大量时间等待交通灯和道路拥挤。传统的A*算法通常忽略了交通灯的问题，其能够获得距离最短的路线，但行程时间不一定最短。

解决这些问题的关键在于修改地图应用中传统A*算法的启发式函数，因此提出了一种基于新的启发式函数的改进A*算法。

1 基本概念

1.1 标题路网

路网定义为N=(I,R)，包括一系列道路交点I={i1,i2,…,in}(作为节点)，通过一系列路段R={r1,r2,…,rn}连接上述节点。其中每个路段ri关联了本身的特征值，包含不同交通状况的衡量指标。

1.2 启发式函数

启发式算法是一种基于直观或经验的局部优化算法，也称为智能算法、现代优化算法[13]，已得到了深入研究和广泛应用，主要包括神经网络算法[14]、遗传算法[15]等。A*算法也是一种启发式算法。算法的共性是基于客观世界中的一些自然现象，通过与组合优化求解进行类比，找出共性设计算法。启发式算法的难点是建立符合实际问题的一系列启发式规则(即启发式函数)，优点在于比盲目型的搜索算法高效。一个经过仔细设计的启发式函数，通常能在较短时间内获得一个搜索问题的最优解。

1.3 欧几里德距离

欧几里德距离(Euclidean distance)指在m维空间中两个点之间的真实距离，或者向量的自然长度(即该点到原点的距离)。在二维和三维空间中的欧氏距离就是两点间的实际距离[16]。在欧几里德平面中，如果两个点为p=(x1,y1)和q=(x2,y2)，则距离由式(1)给出：

(1)

1.4 曼哈顿距离

曼哈顿距离(Manhattan distance)由十九世纪的赫尔曼·闵可夫斯基所创[17]，用以标明两个点在标准坐标系上的绝对轴距总和，是路网中启发式方法通常使用的距离之一。在欧几里德平面中，如果两个点为p=(x1,y1)和q=(x2,y2)，则曼哈顿距离由式(2)给出：

d(p,q)=|x1-x2|+|y1-y2|

(2)

曼哈顿距离相比欧几里德距离，对起点和目标点之间的实际行驶距离会产生更为精确的估计，因为在实际情况中很少存在起点到目标点之间的直接路径，但有时曼哈顿距离也会高估实际距离。

2 A*算法

2.1 基本原理

A*算法是以Dijkstra为基础的启发式搜索方法，是广泛已知的最佳搜索形式[18]。算法的关键创新点在于，在扩展下一个节点时引入路网信息，对当前节点到目标节点的距离进行评估。

基于评估函数f(n)选择节点进行扩展。评估函数解释为成本估算，所以评估最低的节点首先被扩展[19]。评估函数表示如下：

f(n)=g(n)+h(n)

(3)

其中，f(n)为从起始节点经由当前节点n到目标节点状态的成本估计；g(n)为路径从起始节点到当前节点n的实际成本；h(n)为启发式函数，表示从当前节点n到目标节点的最佳路径的估计成本。

对当前节点n的评估方法有多种，如距离、方向、其他指标以及各种指标的综合应用，但是评估的基本原则是评估值与实际值越接近，评估函数的效果越好。

2.2 算法实现

A*算法的流程[20]如图1所示。

(1)建立两个列表存放节点数据(分别为开放列表和关闭列表)；

(2)将初始节点加入开放列表；

(3)寻找初始节点周围所有可到达的节点，跳过关闭列表中的节点，加入到开放列表中；

(4)已访问过的节点加入到关闭列表中；

(5)当开始搜索下一节点时，从开放列表中寻找f值最小的作为下一个扩展的节点(当前节点)；

(6)所有当前节点可到达的节点再次加入开放列表之后，重新比较f值，并且根据f值的大小在开放列表中生成升序排列队列。在搜索过程中，使用广度优先算法[21]依次选取队列的首元素，计算可能子节点的g、h和f值，直到找到目标节点或者没有找到目标节点开放列表已经为空时算法结束。

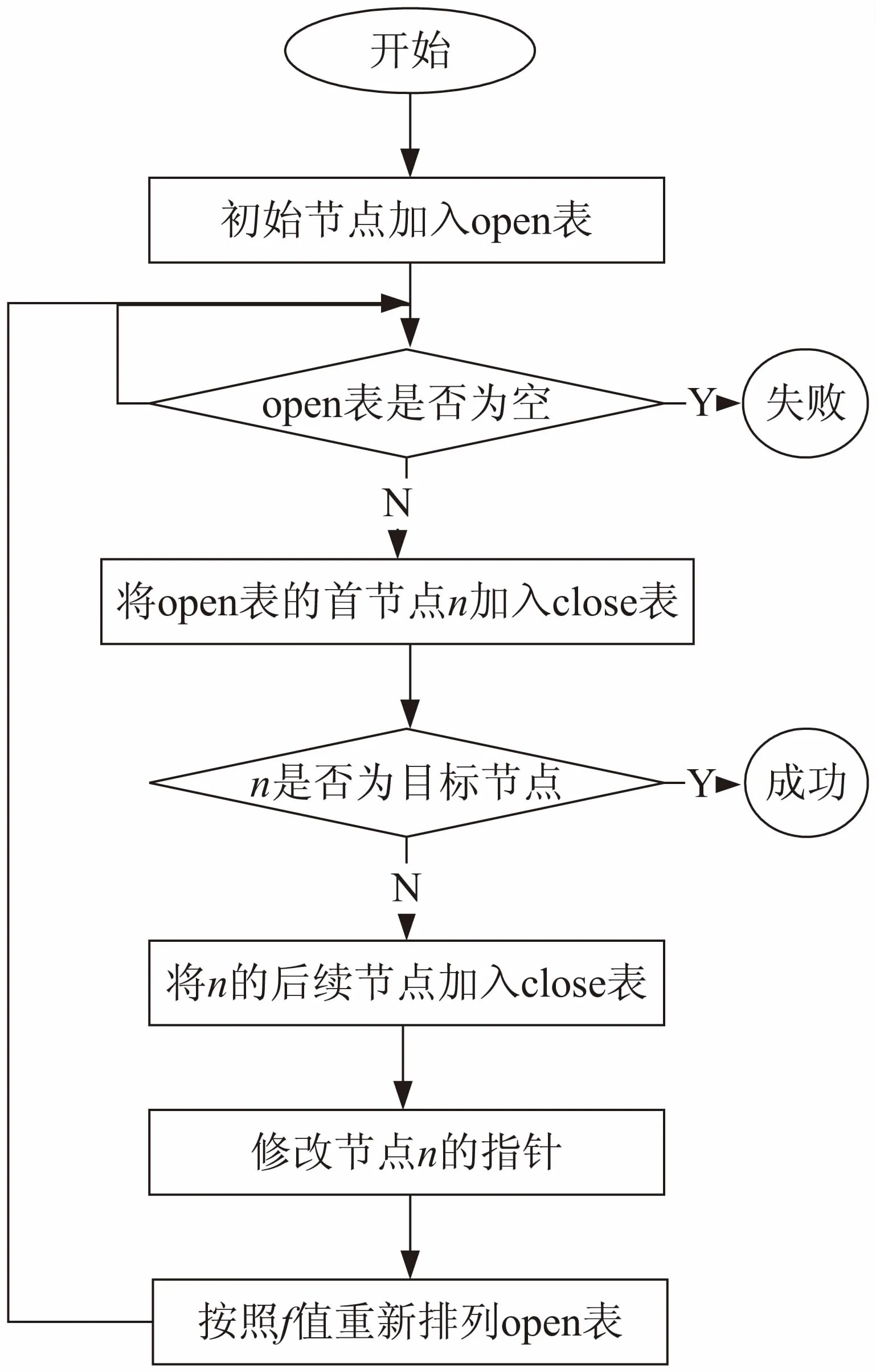
图1 A*算法流程

A*算法实现的具体步骤为：

(1)初始节点加入open表;

(2)从open表中寻找f值最小的节点作为当前节点。当前节点加入到close表的同时将其在open表中删除;

(3)针对当前节点的所有可达节点：(a)若该节点在close表，就跳过该节点，否则进行b；(b)若该节点不在open表中，则将其加入并且使其父指针指向该节点。若该节点在open表中，则计算当前g值，如果比原来g值小，则该节点满足条件。修改其父指针指向新的节点，并计算新的f值和g值，对open表的f值重新进行排序;

(4)在整个搜索过程中，当目标节点已加入close表时，即找到最短路径，此时停止搜索。或者当没有找到目标节点而开放列表已经为空时，即找不到路径，此时也停止搜索;

(5)保存搜索路径的轨迹。通过父指针由目标节点回到初始节点。

3 改进A*算法

算法根据实际路网的条件可以被修改，为了简化路网中的交通灯问题，对于交通灯的假设如下：假设1：每个十字路口都有交通灯。假设2：初始时，交通灯从红灯恰好变成绿灯。假设3：每个交通灯同时具有相同的颜色。假设4：红灯需要1分钟，绿灯需要1分钟。假设5：右转不需要等待交通灯可直接通行。假设6：汽车的平均行驶速度为60英里/小时。假设7：如果交通灯是绿灯，则汽车可以直接穿过该十字路口。

为了实现合理规避交通灯且具有最短行程时间的路径，主要基于传统的A*算法思想，改进原有的距离启发式函数。在改进A*算法中，将总行程时间用作估计成本。估计的行程时间是驾驶时间和等待时间的总和。根据假设6，总驾驶时间可由总驾驶距离除以驾驶速度得到。总等待时间是路网中每个节点上的等待时间的总和。最佳路线是从初始节点到目标节点需要最短时间的路径。

改进A*与传统A*算法之间的关键差异在于增加了等待时间的因素。传统A*算法中，假设汽车可直接通过每个节点而不用等待，然而在实际路网情况中几乎不可能。同时，等待时间与驾驶时间相比不是一个可忽略的时间，特别是在市中心以及道路交通拥堵时(同一个交通灯的等待次数变多)。

假设d(n)是从初始节点到节点n的总行程时间，可通过计算到达节点n前的行程时间总和得到，即从上一节点到节点n的行程时间以及从上一节点到节点n的等待时间。如果汽车进行右转弯，则节点的等待时间为0。否则，将判断该节点的交通灯是否为红灯。根据假设3和4可知，如果行程时间的上限是一个奇整数，则交通灯是绿灯；否则，交通灯是红灯。当交通灯为红灯，必须等到转向绿灯后继续行程。因此，如果行程是从节点u到节点n，可以通过以下函数计算：

d(n)=

(4)

其中，c(u,v)为从节点u到节点v的驾驶时间，可由边长度除以驾驶速度计算得到；w(u)为节点u处的等待时间，可通过开始时间和当前路径从起始节点到节点u的行程时间计算得到。在实验中，假设在初始节点处的交通灯从红灯变成绿灯，不考虑初始时间的影响。

用x来表示节点u的父节点，定义两个向量Vector(x,u)和Vector(u,v)，计算出两个向量的旋转角度。如果是右转弯，转角小于0；如果是左转弯，转角大于0。为了避免直线产生一个角度，定义右转弯角度范围为-135°～-45°。

对于启发式函数，使用曼哈顿距离除以行驶速度作为驾驶时间的估计或者欧几里德距离除以行驶速度作为驾驶时间的估计。

4 实验结果

利用Minneapolis地图数据作为基础数据，地图共有2 326个边和946个节点，边的平均驾驶时间为1.95分钟。地图原始数据使用map.txt存放，其中每一行表示一条边，第一个整数代表道路是否是单行道，后4个数字分别代表一条边的起点坐标和终点坐标。通过程序读取此地图并生成道路网络。实验中的Minneapolis地图如图2所示，其中浅黑线表示单行道和深黑线代表双行道。

图2 Minneapolis地图

由于边的平均驾驶时间为1.95分钟，因此交通灯的等待时间是一个不可忽略的值。实验对比分析了传统的A*算法与改进的A*算法的实现效果，两种算法均分别使用曼哈顿距离和欧氏距离作为启发式函数。算法的对比性能指标是最短路径搜索的运行时间，节点的扩展数量和路径的行程时间。

实验随机选择4个测试样本。在第一个测试样本中，初始点坐标为(1 121,7 568)，目标点坐标为(2 179,8 595)。在第二个测试样本中，初始点坐标为(1 121,7 568)，目标点坐标为(1 455,7 920)。在第三个测试样本中，初始点坐标为(2 197,8 966)，目标点坐标为(1 961,7 800)。在第四个测试样本中，初始点坐标为(2 197,8 966)，目标点坐标为(2 085，8 543)。

通过使用曼哈顿距离和欧几里德距离作为启发式函数的传统A*算法和改进A*算法，来搜索相同样本的最短路径。4种算法的性能实验结果如表1～4所示。第三个测试样本中利用4种算法搜索的最短路径结果如图3所示，其中粗灰色线代表最短路径。

5 结果分析

对实验结果的综合分析发现：4种算法的运行时间均在大致相同的规模内(毫秒级)。运行时间的结果和节点扩展数量表明，改进A*算法与传统A*算法能在类似的时间范围内执行计算，并扩展相同数量的节点；传统A*算法比改进A*算法运行时间更快，分析其原因是：考虑到交通灯等待时间之后，改进A*算法中有更复杂的g(n)和h(n)需要计算，略微(在毫秒级)影响了算法的运行时间;(3)两种使用曼哈顿的算法与两种使用欧几里德的算法相比在距离上扩展了较少的节点，且运行时间较短，表明曼哈顿距离相比欧几里德距离在运行时间方面具有更好的估计效果。

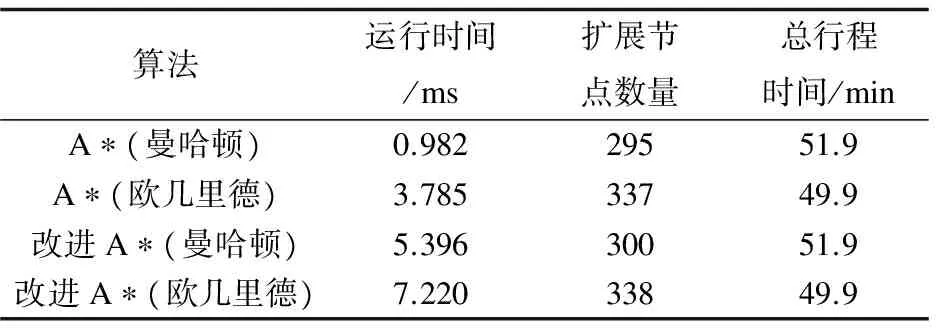
表1 节点(1 121,7 568)到节点(2 179,8 595)的实验结果

表2 节点(1 121,7 568)到节点(1 455,7 920)的实验结果

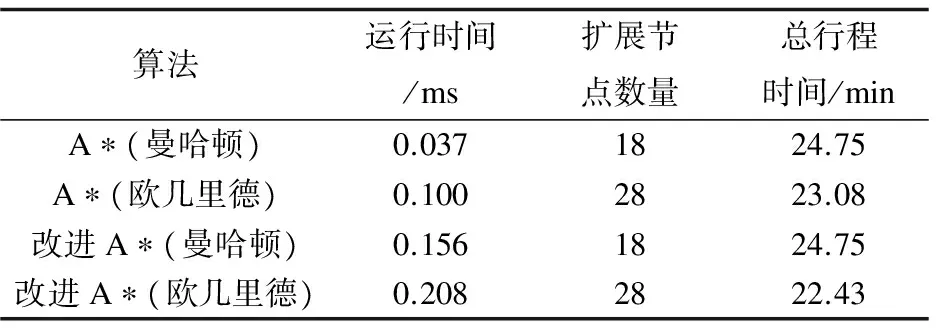
表3 节点(2 197,8 966)到节点(1 961,7 800)的实验结果

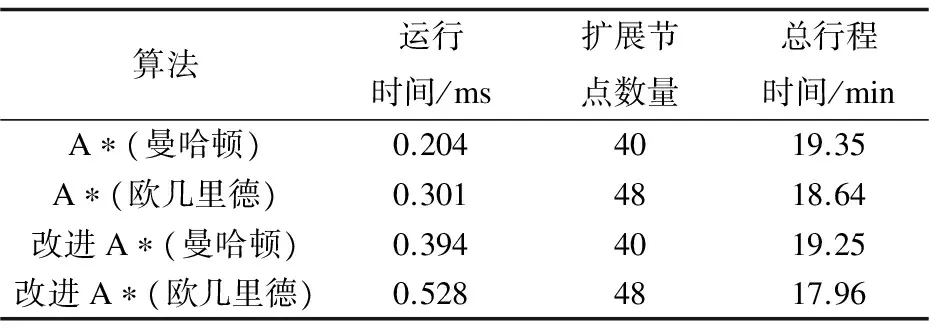
表4 节点(2 197,8 966)到节点(2 085,8 543)的实验结果

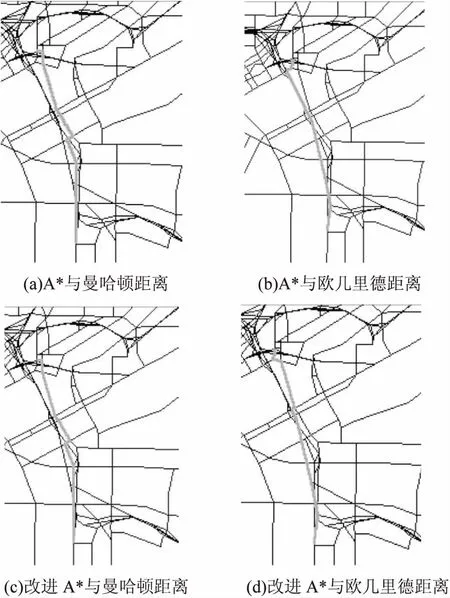
图3 搜索结果

上述表明：传统A*算法与改进A*算法均能够实现最短路径的搜索，且运行时间和扩展节点数量相差不大，在这两方面性能相似。为了缩短用户在路网的行程时间，文中着重关注两类算法在性能-总行程时间上的差异(min级)。

结合分析第3个和第4个测试样本，实验发现：使用欧几里德距离的启发式函数的改进A*算法能搜索到最少行程时间的路径，改进A*算法的总行程时间与传统A*算法相比减少约5%，表明文中提出的方法在总行程时间方面更有效。分析其原因是：文中算法改进了等待交通灯的时间，其次是由于曼哈顿距离相对于欧几里德距离会产生一部分过高估计，从而影响到算法的行程时间。

因此最好使用欧几里德距离作为启发式函数的改进A*算法，其始终能提供最佳行程时间路径。从图3中看出，不同方法搜索到的最短路径是不同的，而最优路径会有一些右转弯，以避免交通灯的等待时间。

6 结束语

文中致力于改进和完善传统的最短路径搜索A*算法，克服路网中交通灯的等待问题，在启发式函数中加入交通灯的等待时间，并融合到传统的A*算法中进行最短路径搜索。通过传统算法与改进A*算法的对比实验证明，文中提出的算法能实现最短路径的搜索且具有较短的行程时间，并与传统算法能够在同一运行时间限制下实现。对基于A*算法的研究具有一定的理论价值，并且丰富了路网最短路径搜索领域的内容。

参考文献：

[1] SHEHZAD F,SHAH M A A.Evaluation of shortest paths in road network[J].Pakistan Journal of Commerce & Social Sciences,2009,3:67-79.

[2] FARO A,GIORDANO D.Algorithms to find shortest and alternative paths in free flow and congested traffic regimes[J].Transportation Research Part C Emerging Technologies,2016,73:1-29.

[3] ZHANG X,GUO X,JING G,et al.Research of improved shortest path algorithm in campus GIS[J].Open Cybernetics & Systemics Journal,2015,9(1):1060-1063.

[4] XU W,HE S,SONG R,et al.Finding the K shortest paths in a schedule-based transit network[J].Computers & Operations Research,2012,39(8):1812-1826.

[5] YANG H H,CHEN Y L.Finding K shortest looping paths in a traffic-light network[J].Computers & Operations Research,2005,32(3):571-581.

[6] WANG S X.The improved Dijkstra’s shortest path algorithm and its application[J].Procedia Engineering,2012,29:1186-1190.

[7] 赵礼峰,梁 娟.最短路问题的Floyd改进算法[J].计算机技术与发展,2014,24(8):31-34.

[8] SHAHZADA A,ASKAR K.Dynamic vehicle navigation:an A* algorithm based approach using traffic and road information[C]//International conference on computer applications and industrial electronics.[s.l.]:IEEE,2011:514-518.

[9] GUTMAN R J.Reach-based routing:a new approach to shortest path algorithms optimized for road networks[C]//Workshop on algorithm engineering & experiments & the first workshop on analytic algorithmics & combinatorics.[s.l.]:[s.n.],2004:100-111.

[10] ZHU A D,MA H,XIAO X,et al.Shortest path and distance queries on road networks:towards bridging theory and practice[C]//ACM SIGMOD international conference on management of data.New York,NY,USA:ACM,2013:857-868.

[11] ANWAR T,LIU C,VU H L,et al.RoadRank:traffic diffusion and influence estimation in dynamic urban road networks[C]//ACM international conference on information and knowledge management.New York,NY,USA:ACM,2015:1671-1674.

[12] 王先美.交通灯控制系统的设计[J].科技传播,2010(23):114.

[13] 陈 萍.启发式算法及其在车辆路径问题中的应用[D].北京:北京交通大学,2009.

[14] 冯立颖.改进的BP神经网络算法及其应用[J].计算机仿真,2010,27(12):172-175.

[15] 马永杰,云文霞.遗传算法研究进展[J].计算机应用研究,2012,29(4):1201-1206.

[16] 徐士英.关于欧几里得空间Ed中的二距离集[J].中国计量学院学报,2002,13(1):16-18.

[17] 李 彬.基于相对曼哈顿距离的Web聚类算法研究[J].电子商务,2013(11):57-58.

[18] 熊 伟,张仁平,刘奇韬,等.A*算法及其在地理信息系统中的应用[J].计算机系统应用,2007,16(4):14-17.

[19] 刘 浩,鲍远律.A*算法在矢量地图最优路径搜索中的应用[J].计算机仿真,2008,25(4):253-257.

[20] 杨银涛.基于A*算法的避障应用仿真[D].郑州:郑州大学,2014.

[21] 欧阳圣，胡望宇．几种经典搜索算法研究与应用[J]．计算机系统应用,2011,20(5):243-247.