拓扑结构与节点属性综合分析的社区发现算法
张振宇,朱培栋,王 可,胡慧俐
(国防科学技术大学 计算机学院,湖南 长沙 410073)
0 引 言
20世纪90年代以来,国际互联网、社交网络、新陈代谢网络、电力网络、交通网络、脑细胞网络等使得人们生活的世界处于各种不同类型的复杂网络之中,对各类复杂网络性质的研究随之成为必要。社交网络中社区结构的发现,不仅有助于网络功能的发掘、网络内部连接层次的识别、社交网络上复杂用户行为及群体行为的理解[1],同时其分析理论也广泛应用于其他学科。
现有的一些经典社区发现算法,如GN算法、FastNewman算法、遗传算法、系派过滤法、纽带社区等,均只是基于网络拓扑结构[2]进行社区发现。但是,社交网络节点往往蕴含丰富的属性信息,这些信息对社区结构的形成具有重要影响,目前带有节点属性的社区发现,如基于随机游走的边权值节点属性相似度NAS算法[3],衡量拓扑结构和节点属性的距离概念[4],边稳定稀疏模型[5],联合拓扑和属性的分析[6],这些均将节点属性作为影响因素进行了考虑,但都没有很好地解决两者之间的相关关系,使其联合分析无可避免地产生相关性误差。目前联合拓扑结构和节点属性的社区发现技术有待进一步深入分析。
文中综合考虑社交网络中的拓扑结构和节点属性,通过对两因素进行去相关性操作和赋权处理,从而建立社交网络的社区距离关系矩阵,最后针对得到的关系矩阵,设计一种依据模糊关系相关原理的社区发现算法。该算法具有较高的社区发现准确率,并通过不同阈值的选定能得到多层次社区结构[7],解决社区层次性问题。
1 问题描述
对社交网络进行精准的描述是社区发现的基础。可用图结构对社交网络进行描述,用WG=(V,E,W,S)表示社交网络[8],其中V为图节点集合,表示人;E为图边集合,表示人与人之间的社交关系;W为图边权值,表示关系的强弱;S为图节点信息,表示人对应的属性信息。
社区结构是一种网络拓扑特性,刻画了连边关系的局部聚类特性。为了发现或识别社区结构,如果能够判定任意两个节点是否处于同一社区,那么该社区结构也就唯一确定。用矩阵描述为P=[pij]n×n,其中pij∈{0,1},0表示对应两人处于不同社区,1表示对应两人处于相同社区。需要指出的是:每个人和自己必定处于相同社区;如果A与B处于相同社区,那么B与A也处于相同社区,反之亦然;如果A与C处于相同社区,B与C也处于相同社区,那么B与C亦处于相同社区。
将上述三个条件符号化:矩阵P中,若pii=1,即满足自反性;若pij=pji,即满足对称性;若pij=1,pjk=1,则有pik=1,即满足传递性。故反映社区结构的矩阵P是普通等价矩阵。
由此,可将问题进行如下描述:
f(W,S)=P
(1)
其中,W表示网络拓扑结构;S表示网络节点属性;P表示社区结构,为普通等价矩阵;函数f表示网络拓扑结构和节点属性到社区结构的映射关系,即为所求。
2 网络社区距离
从社交网络的拓扑结构和节点属性出发得到社交网络的社区结构。为避免社区发现结果受影响因子间相关性的影响,本节对影响因子进行去相关性分析;同时,基于设计的稳定性赋权方法综合拓扑结构和节点属性。
2.1 拓扑结构与节点属性的相关性分析
对于节点属性,同社区的属性相似度相对较高,不同社区的属性相似度相对较低,因此,相较于属性值,属性相似性更能体现网络的社区情况。文中用欧氏距离描述属性相似性。
综合拓扑结构和节点属性进行社区结构发现时,两者之间的相关性容易为后面的综合讨论带来叠加效应[3]。目前社交网络中关系的量化并没有形成统一的标准,量化误差会使得关系数据偏离理论上的正态分布;节点属性的量化赋值方法具有极大的主观性,使得属性总体分布类型未知。因此,采用Spearman相关系数对两者之间的相关性进行度量。Spearman相关系数用于对不服从正态分布的数据、总体分布类型未知的数据的关联性进行描述。
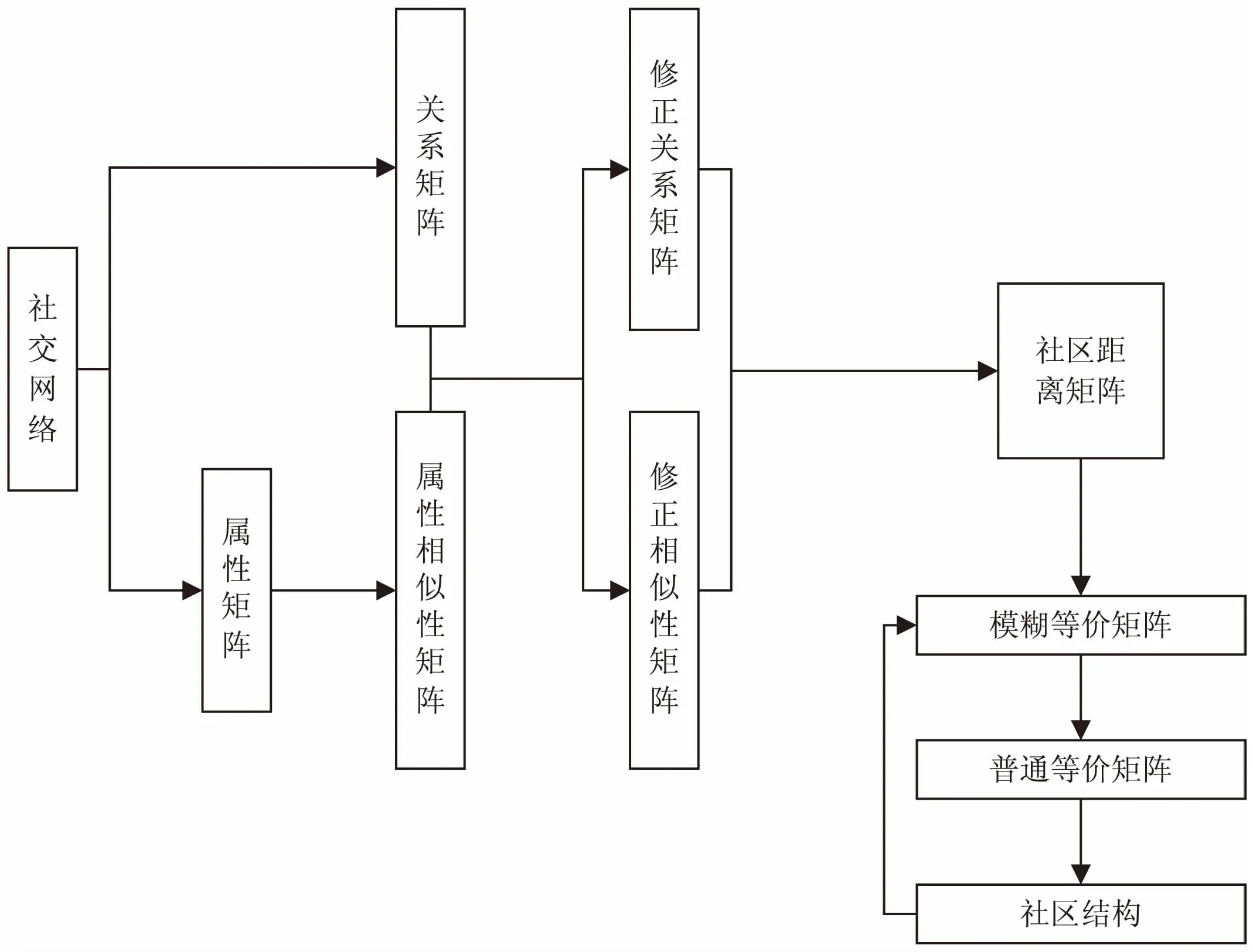
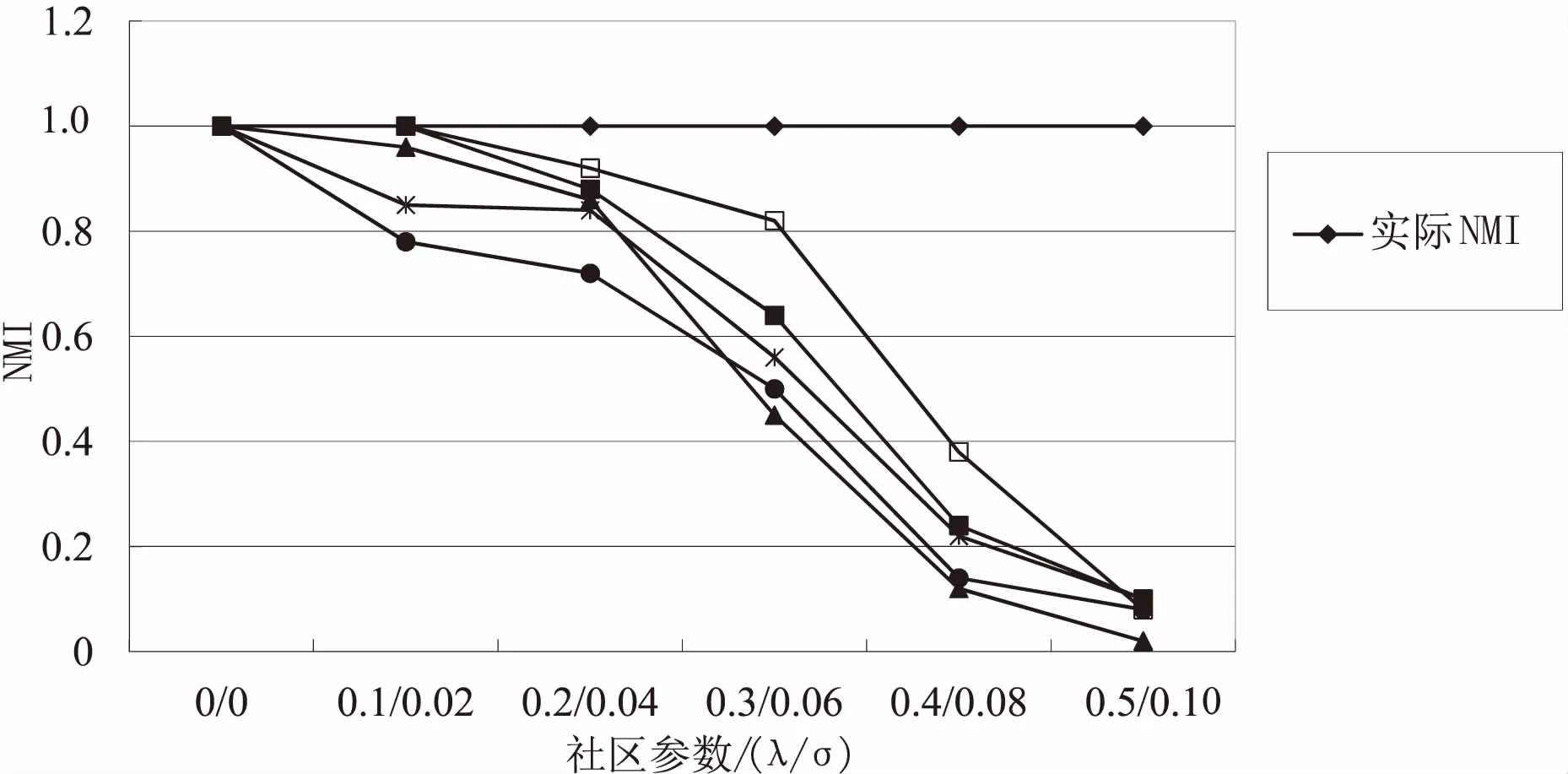
取X和Y两个集合对应表示矩阵W和N中的数值,Xi、Yi为对应集合中的第i(0 (2) 基于上述分析,通过如下操作进行相似性和去相关性处理: (3) (4) 此时,对于问题的求解,得到如下过程: f1(W,S)=(W,N) (5) 其中,W为关系强度矩阵;S为网络节点属性矩阵;N为强度无关属性矩阵;函数f1为相关性剔除函数,是函数f的分函数。 所研究问题的难点在于如何确定两影响因素对社区结构的影响程度。针对不相关变量的综合处理,目前有多种解决方法,但是,大部分方法中的权重需要主观赋予,而社交网络很难从机理的角度得到二者对社区结构之间的影响权重,故该类方法对于本问题具有较大主观性。 (6) 前文只分析了两节点间的直接关系对社区结构形成的影响,而社区结构其内部节点的聚类系数很高,社区聚类系数由节点间的间接关系反映。因此,把节点间的间接关系作为社区结构形成的另一影响因素,同时,由于社交网络的小世界性,认为三度(及以上)邻居关系的影响较小。用该对节点与其他节点的距离的差方和来衡量两度邻居的影响因子: (7) (8) 文中提出“社区距离”的概念[9]。根据以上分析,综合稳定性赋权和聚类系数操作,根据式(6)~(8)提出反映两节点的社区情况的社区距离,定义如下: (9) 其中,σN为矩阵N元素的方差;σW为矩阵W元素的方差;lij为节点i与节点j之间的社区距离。得到社区距离矩阵L=[lij]n×n。 此时,对于问题的求解,得到如下过程: f3(W,N)=L (10) 其中,W为关系强度矩阵;N为强度无关属性矩阵;L为网络社区距离矩阵;函数f3为社区距离函数,是函数f的分函数。 文中最终要得到的社区结构是一种普通等价关系,而社区距离矩阵L也是一种关系的表现,因此,文中社区发现的过程实质是关系变换的过程,即从普通关系变换为等价关系。本节基于模糊关系相关理论对网络数据进行分析,从而进行社区发现。 将社区距离矩阵Ln×n表示为节点集V×V中的模糊关系。在该模糊关系中[10],lij∈[0,1],lii=0,lij=lji,此模糊关系只满足对称性。 欲使关系满足自反性,令lii=1,此时,lij∈[0,1],lij=lji,lii=1,该矩阵同时满足对称性、自反性,为模糊相似矩阵。 此时,对于问题的求解,得到如下过程: f4(L)=Ln-1 (11) 其中,L为网络社区距离矩阵;Ln-1为L的n-1次max-min乘积[13];函数f4为模糊传递闭包函数,是函数f的分函数。 文中需要得到能反映社区结构的普通等价矩阵,模糊数学中的截关系运算可以完成。令L是V×V中的模糊关系,对任意α∈[0,1],其α截关系Lα的特征函数为: (12) 由此,在没有改变关系的等价性的前提下,模糊关系转化为确定关系,最终得到明确的节点划分关系—社区结构。有必要指出:基于不同的截取值,会有不同的社区结构,即该社区发现具有多层次性。 此时,对于问题的求解,得到如下过程: f5(Ln-1)=P (13) 其中,P为社区结构矩阵;函数f5为截运算函数,是函数f的分函数。 从拓扑结构和节点属性出发,对该影响因素进行相关性分析、权值赋予讨论,通过模糊关系相关理论进行社区发现,给出一种新的社区结构发现方法,算法模型如下: f(W,S)=f4(f3(f2(f1(W,S))))=P (14) 其中,W表示网络拓扑结构;S表示网络节点属性;P表示社区结构;f1为相关性剔除函数;f2为社区距离函数;f3为模糊传递闭包函数;f4为截运算函数。 文中社区发现模糊算法的具体描述如下: 输入:连接矩阵W,属性矩阵S 输出:社区结构P 2.defineD=排序差分(W,N') 3.defineρ=Spearman相关系数(D) 5.for(i,j双循环) 6.for(n次循环)defineλij=λij+[1-(wik-wjk)]2/n 7.defineγij=γij+[1-(nik-njk)]2/n; //三度邻居关系 8.defineσW=(W的方差);σN=(N的方差); 9.σW=σN/(σW+σN);σN=σW/(σW+σN) //基于稳定性赋权 10.for(i,j双循环) 11.definelij=σWλijwij+σNγijnij//综合权值拟合 12.for(n-1次循环) 13.for(i,j双循环) 15.define(α=input) 17.elsepij=0 //模糊截关系处理 18.if(P==预期) over //社区层次性选择 19.else 返回(15) 20.returnP 算法流程如图1所示。从社交网络出发,得到社交网络中反映拓扑结构的关系矩阵和反映节点属性的属性矩阵;对属性矩阵进行相似性变换得到属性相似性矩阵;对关系矩阵和属性相似性矩阵进行相关性分析得到修正关系矩阵和修正相似性矩阵;对两修正矩阵进行赋权处理得到社区距离矩阵;对社区距离矩阵进行模糊传递闭包处理得到模糊等价矩阵;进而基于截关系得到能够反映社区结构的普通等价矩阵。 图1 算法流程 文中算法与各经典算法基于不同的数据集进行比较分析。基于HOT模型[14]得到网络模拟数据,社区评价指标为模块度与NMI[15]。模块度是社区内部的总边数和网络中总边数的比例减去一个期望值,用于在不知道网络真实划分的情况下量化或评判的社区划分水平。NMI是归一化互信息,用于衡量算法划分结果和真实结果的重合程度;通过模拟数据集进行实验;基于不同社区参数和网络规模下[16]的社交网络进行实验结果以及时间复杂度比较如图2~4及表1所示。 图2 不同社区度网络下各算法的模块度 图3 不同社区度网络下各算法模块度NMI 图4 不同规模网络下社区模块度 表1 各算法时间复杂度 由图2可以看到,不同社区参数下,文中算法得到的社区结构的模块度较高,且对社区参数不敏感;由图3可以看到,不同社区参数下,文中算法得到的社区结构的NMI较高,且对社区参数较敏感,社区参数较大时下降较快;由图4可以看到,不同网络规模下,文中算法得到的社区结构的模块度低于遗传算法但均好于其他算法,且对网络规模相对不敏感;由表1可以看到,文中算法时间复杂度相对较高,不太适用于大规模网络分析,这也是后续工作中应该关注和改进的方向。 由此,相比各算法,文中算法时间复杂度相对较高,算法准确率高且稳定,对网络规模和网络聚类性不敏感,具有较高的准确性,适用于小型网络、中型网络以及对时间要求不高的大型网络的社区发现。 从包含拓扑结构和节点属性的完备信息集出发,通过相似性运算、去相关性运算、赋权运算等操作进行数据前期处理;基于模糊传递闭包思想进行社区结构的发现,通过截运算得到社区结构;最终实现了社交网络的社区发现,同时一定程度上解决了社区层次性的问题,缓解了网络动态性带来的影响。 该算法基于网络拓扑结构和节点属性信息,增强了信息完备度;设计的稳定赋权法和Spearman相关系数的引入解决了信息干扰问题;社区距离概念的提出和模糊关系理论的导入提升了社区发现的精度和稳定性。 参考文献: [1] AHN Y Y,BAGROW J P,LEHMANN S.Link communities reveal multiscale complexity in networks[J].Nature,2010,466(7307):761-764. [2] 刘大有,金 弟,何东晓,等.复杂网络社区挖掘综述[J].计算机研究与发展,2013,50(10):2140-2154. [3] STEINHAEUSER K,CHAWLA N V.Identifying and evaluating community structure in complex networks[J].Pattern Recognition Letters,2010,31(5):413-421. [4] ZHOU Y,CHENG H,YU J X. Graph clustering based on structural/attribute similarities[J].Proceedings of the VLDB Endowment,2009,2(1):718-729. [5] 林友芳,王天宇,唐 锐,等.一种有效的社会网络社区发现模型和算法[J].计算机研究与发展,2012,49(2):337-345. [6] 郭进时,汤红波,葛国栋.一种联合拓扑与属性的社区模糊划分算法[J].计算机工程,2013,39(11):35-40. [7] 王 莉,程学旗.在线社会网络的动态社区发现及演化[J].计算机学报,2015,38(2):219-237. [8] 于 海,赵玉丽,崔 坤,等.一种基于交叉熵的社区发现算法[J].计算机学报,2015,38(8):1574-1581. [9] HU R J,LI Q,ZHANG G Y,et al.Centrality measures in directed fuzzy social networks[J].Fuzzy Information and Engineering,2015,7(1):115-128. [10] 范艳焕,耿生玲,李永明.Pebble模糊有穷自动机和传递闭包逻辑[J].模糊系统与数学,2015,29(4):38-44. [11] 李秀格,朱红宁.求模糊相似矩阵的传递闭包的简捷算法[J].电脑知识与技术,2014,10(26):6161-6164. [12] PARAND F A,RAHIMI H,GORZIN M.Combining fuzzy logic and eigenvector centrality measure in social network analysis[J].Physica A:Statistical Mechanics and Its Applications,2015,459:24-31. [13] RAJ E D,BABU L D D.A fuzzy adaptive resonance theory inspired over lapping community detection method for online social networks[J].Knowledge-Based Systems,2016,113:75-87. [14] 吴增海.社交网络模型的研究[D].合肥:中国科学技术大学,2012. [15] 王 林,戴冠中,赵焕成.一种新的评价社区结构的模块度研究[J].计算机工程,2010,36(14):227-229. [16] 岳 训,迟忠先,莫宏伟,等.基于网络社区模块结构的特征选择性能评价[J].计算机工程,2007,33(12):16-18.
2.2 网络社区距离指数
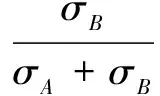

3 基于模糊关系的社区发现
3.1 社区距离的模糊等价化

3.2 模糊关系确定化
4 算法描述
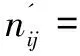
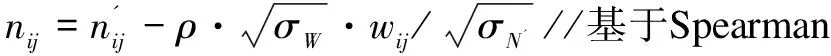

5 算法实现与分析



6 结束语

