诱导二元语义广义概率有序加权平均算子在财务管理决策中的应用*
李肖瑞, 冷欧阳
(1. 郑州工业应用技术学院 商学院, 郑州 451199; 2. 国家电网公司 呼伦贝尔供电公司, 内蒙古 呼伦贝尔 021008)
在当今的商业环境下,各种企业所面临的竞争环境同样激烈,如果不想被别的企业所取代必须制定相应的对策。在这种大环境下,财务管理决策这个对于企业生存与发展至关重要的管理决策问题越来越被人们重视。在企业的有关资金方面,最重要的包括投资、筹资、经营运作以及利润分配。企业财务管理中的各项活动都涉及到财务决策问题,良好的财务决策有助于企业构建优效的经营机制、确立恰当的发展战略、合理运作资金,并且强迫企业在竞争中求发展,使得自己的优势产品做得更好,并且能够在这个过程中获得更大的经济效益,在市场中立于不败之地。企业的财务决策不是单个人或单方面决定的结果,而是由多人共同参与决策分析并制定决策的整体过程,因此是一个群决策问题。
在相当多的方面(如关于群的决策),国外学者对OWA算子进行整合,并且提出了IOWA算子[1]和GOWA算子[2]。IOWA算子根据诱导变量进行参数的重新排序,反映了决策者的重要性和决策的准确性,解决了之前OWA算子中依靠参数进行决策分析的问题;而GOWA是经典OWA算子的直接拓展。这两类集结算子使得信息的表达和处理更具有实用性。近年来,有关这两类算子的研究已引起学者的高度重视,如周礼刚等提出的诱导连续区间有序加权平均算子的应用[3]等。现在很多学者提出将广义有序的IGOWA算子应用到多属性群的决策中[4-5]。伴随着有关学者研究的进一步加深,某国外学者在广义平均的基础上提出了IGOWA算子[6],并在此基础上提出了POWA算子[7]和TWO-TLIGOWA算子[8],这些算子都是OWA算子的延伸。
现在,IGOWA算子的多属性群决策探究能够较好地反映信息结合过程,对于概率信息,Merigó介绍了语言概率序列加权平均(ILPOWA)算子[9],但尚缺乏2TLIGOWA算子和2TLGPWA算子的结合。本文对于准则值是二元语义的情况,利用概率信息和诱导变量建立相应的集结算子。
如何计算算子权重同样是探究集结算子时的一个关键问题。许多学者致力于研究如何确定算子属性权重,常用的方法有最小方差法[10]、最小离差法[11]、贝叶斯最大熵法[12]以及一些拓展的权重方法,如加权函数法[13]、最小距离法[14]、改进的极大极小差距模型[15]等。这些方法的共同特点是从公平性角度出发确定权重,换言之,所有属性都应该被认为是同样重要的,这显然存在不合理之处。例如,在实际决策矩阵中,对于一个给定的属性,若在同一个属性下每一个方案的属性值几乎相同,则这个属性在方案选取时起到的作用比较微弱,应该给予它一个比较小的权重;相反地,如果该性质值差异较大,则应赋予一个较大的权重。为此,本文结合公平性,并同时兼顾属性值的差异性,提出一个非线性二次偏差最优定权模型。进而,本文结合集结算子和权重定权模型,提供了基于2TLIGPOWA算子的财务管理决策办法。最后,通过算例分析并证明了本文该方法的有效性。
一、预备知识
1. 二元语义及其集结算子
二元语义使用一个二元组(si,ai)表示语言评价信息[16]。其中,si表示点评信息汇合的语句,ai表示计算出来的语句与开始语句点评集中最相近语句之间的差异,此差别是[-0.5,0.5)内的数,即符号平移的观点[17-18]。接下来对二元语义进行详尽的说明。
定义1若si∈S是一个语句,θ为S→S×[-0.5,0.5),则相对应的二元语义公式为
θ(si)=(si,0) (si∈S)
(1)
定义2设实数β∈[0,g]表示语句集结运算的成效,g+1表示集合S中元素个数,称(si,ai)为与β相对应的二元语义方式,Δ为[0,g]→S×[-0.5,0.5),则有
Δ(β)=(si,ai)
(2)
式中:i=round(β),round表示四舍五入取整算子;ai=β-i,ai∈[-0.5,0.5)。
定义3设(si,ai)是一个二元语义,则si是S中第i个元素,ai∈[-0.5,0.5),存在逆函数Δ-1为S×[-0.5,0.5)→[0,g],使之转换为相对应的数,β∈[0,g],即
Δ-1(si,ai)=i+ai=β
(3)
假设(si,ai),(sj,aj)为两个二元语义,则有如下性质:
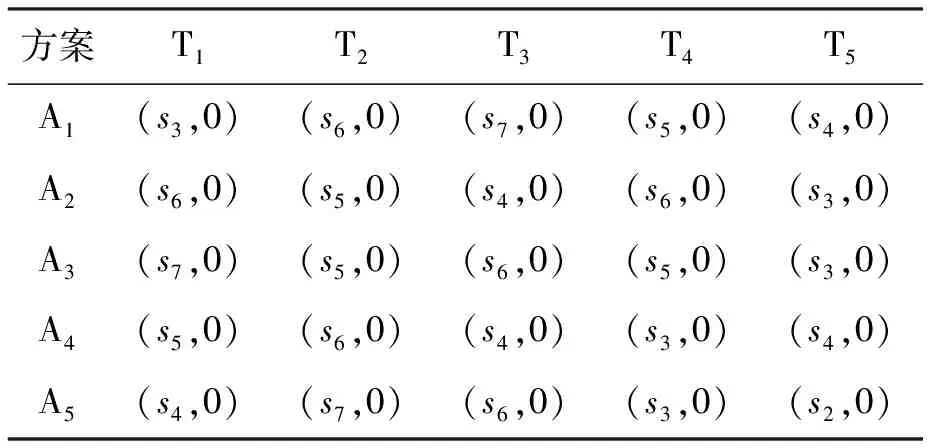
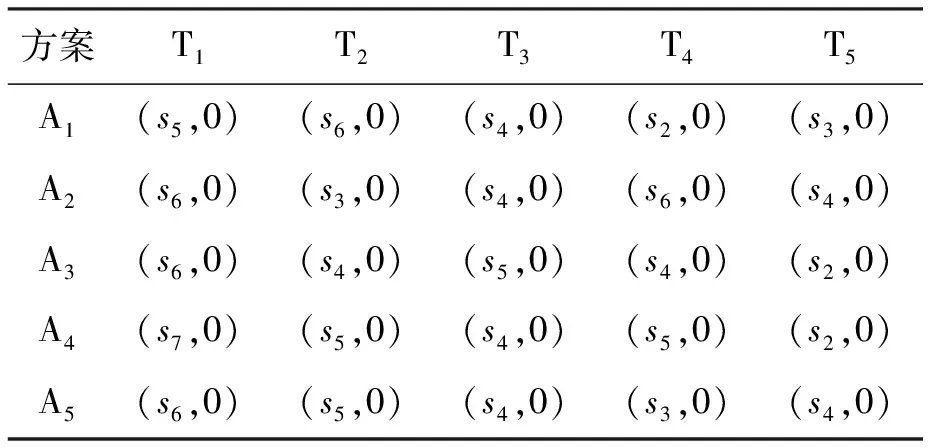
(1) 若i (2) 若i=j,ai=aj,则(si,ai)=(sj,aj);ai 2. IOWA算子 OWA算子的另一个方式是利用诱导因子,得到诱导有序加权平均(IOWA)算子,n元函数IOWA的映射Sn→S满足 IOWA((u1,a1),(u2,a2),…,(un,an))= (4) IOWA算子所采用的集结方式如下:通过(ui,ai)中的诱导变量ui的数值大小排列顺序来对IOWA算子进行排序,再根据ai进行有序加权的集结。aj的大小与位置并不影响wj,wj只受诱导变量所处位置的影响[19-20]。在上述过程中,IOWA算子区别于OWA算子之处为:IOWA算子通过诱导变量来进行排序,而OWA算子则通过数据值大小来进行排序。在一般情况下,现实决策过程中的诱导变量可以体现决策者的重要性或者其所作决策的精确性。因此,相比而言IOWA算子的排序方法更为合理。 3. POWA算子 POWA算子是在考虑每一个概念重要程度的时候利用概率和OWA的集结所构成的一种集结算子[21-22],n元函数POWA的映射Sn→S满足 (5) 根据不同权重向量的选取,可得到多种类型的POWA算子。特别情况下,若β=0,得到概率集结算子;若β=1,则得到OWA算子。 1. ILPOWA算子 Merigó定义了ILPOWA算子,它是语言概率平均(LPA)算子和诱导IOWA算子的结合[23],在同一个表达式中根据每个概念重要性进行分析。因此,它能够以概率和决策者的态度特征来表达客观信息,同时能够使用语言变量进行不确定信息表达,表达式为 ILPOWA((u1,sa1),(u2,sa2),…,(un,san))= (6) 2. 2TLIGPOWA算子 在复杂环境下进行多属性群决策时,往往不能实现精确评价,决策者希望评价值越精确越好。为了更好地提高算子的适用性,将多种不同信息的集成算子通过适合的控制参数整合到一个函数表达式里,再通过对控制参数的调整让决策者获得对应的调整结果,不同的参数取值对应着不同的信息集成算子[24-25]。通过上述研究内容,本文提出了一个有所拓展的集成算子,即诱导二元语义广义概率有序加权平均(2TLIGPOWA)算子。 定义4n元函数2TLIGPOWA的映射Sn,Sn→S满足 2TLIGPOWA((u1,(s1,a1)),(u2,(s2,a2)),…, (7) 2TLIGPOWA算子由2TLIGOWA算子和2TLGPWA算子两部分组成,具体为 2TLIGPOWA((u1,(s1,a1)),(u2,(s2,a2)),…, (8) 式中:bj为第j大的ui所对应的bi,bi=Δ-1(si,ai),β∈[0,1]。 假设有粒度为7的语言术语集S={s0=很差,s1=差,s2=稍差,s3=相当,s4=稍好,s5=好,s6=很好};相应的诱导集结变量(ui,(si,ai))为((5,(s2,0)),(7,(s4,0)),(2,(s3,0)),(9,(s6,0)));w=(0.2,0.2,0.3,0.3)为权重向量,概率权重为v=(0.3,0.3,0.2,0.2),λ=1。其中,概率信息的重要程度为60%,2TLIGOWA中权重向量w的重要程度为40%,利用2TLIGPOWA算子集结,结果为 2TLIGPOWA= 0.4(0.2s6+0.2s4+0.3s2+0.3s3)+ 0.6(0.3s2+0.3s4+0.2s3+0.2s6)= s3.56 (9) 需要注意的是,当权重向量没有标准化时,2TLIGPOWA能够表达为 2TLIGPOWA((u1,(s1,a1)),(u2,(s2,a2)),…, (10) 2TLIGPOWA既单调、有界,也具有置换不变性、幂等性。 定理1(单调性) 设f是2TLIGPOWA算子,如果(sxi,axi)≥(syi,ayi)(i=1,2,…,n),则 f((u1,(sx1,ax1)),(u2,(sx2,ax2)),…, (un,(sxn,axn)))≥f((u1,(sy1,ay1), (u2,(sy2,ay2),…,(un,(syn,ayn))) (11) bimin≤ f((u1,(s1,a1)),(u2,(s2,a2)),…, (un,(sn,an)))≤bimax (12) 定理3(置换不变性) 设f是2TLIGPOWA算子,(syi,ayi)是(sxi,axi)的任一置换,则 f((u1,(sx1,ax1)),(u2,(sx2,ax2)),…, (un,(sxn,axn)))=f((u1,(sy1,ay1), (u2,(sy2,ay2),…,(un,(syn,ayn))) (13) 定理4(幂等性) 设f是2TLIGPOWA算子,对于任意i,均有(si,ai)=(s,a),则 f((u1,(s1,a1)),(u2,(s2,a2)),…, (un,(sn,an)))=(s,a) (14) f((u1,(s1,a1)),(u2,(s2,a2)),…,(un,(sn,an)))= 许多研究者致力于研究算子属性权重,常用的属性权重确定方法有最小方差法、最小离差法、贝叶斯最大熵法以及一些拓展的权重方法,如加权函数法、最小距离法、改进的极大极小差距模型等,这些方法的共同特点是从公平性角度确定权重,换言之,所有属性都应该被认为是同样重要的[26]。但上述方法忽略了输入变量信息对确定属性权重的影响,即他们均认为属性值的分布对确定属性值没有影响。例如,对于两个矩阵X1和X2(X2是由X1的列向量互换得到),即 若按照上述学者的定权模型,对X1和X2中相同属性,将会得到相同的权重,这显然存在不合理之处。 此外,在实际决策矩阵中,对于一个给定的属性,若在同一个属性下每一个方案的属性值几乎相同,那么在选择方案时该属性作用不大,权重赋予得应当较小一点;反之,倘属性值差入较大,则对该属性应赋予一个较大的权重。为此,本文考虑公平性并兼顾属性值的差异性,创造性地提出一个非线性二次偏差最优定权模型,即 (15) 式中:k1,k2为相对重要程度;Dij为规范化处理后的属性值。 当k1=0时,表示决策者希望每一个属性权重尽可能相等。当k2=0时,表示决策者希望属性所有偏差最大化。 ILPOWA算子与2TLIGPOWA算子的异同可归纳为以下诸点。 相同点:(1)模糊环境下的属性值描述是以语言变量来表征的。(2)均考虑了概率信息和诱导变量进行多属性决策。 不同点:(1)拓展的ILPOWA算子是在语言变量的基础上进行细化,利用二元语义进行属性值的描述,使属性值更加精确。(2)参数λ不一样的取值可表征不一样的集结算子,扩增ILPOWA算子的可用范围,ILPOWA算子是2TLIGPOWA算子的一特例。(3)搭建了一个新的权重模型,使决策更与实情相符。 2TLIGPOWA算子的主要优点在于它能够在不精确的环境下,利用概率和决策者的态度特征来分析语言信息,即它能够在分析风险和不确定问题时形成一个语言决策。基于2TLIGPOWA算子的财务管理决策方法如下: 步骤1A={a1,a2,…,am}作为方案集,T={T1,T2,…,Tn}作为方案的性质或属性,构成评价矩阵sk。 步骤4归一化处理该综合评价矩阵,再以式(9)来确定属性权重。 步骤5利用2TLIGPOWA算子对应的公式进行计算,按照之前的计算步骤选择最好的决策结果,同时,将方案按照从最优到最差进行排序,以便于选取多个方案时的灵活运用。 该方法是有普适性的,它可用于财务投资、融资、经营及利润分配等财务管理各方面。 本文以电力企业的财务投资为例,来检验基于2TLIGPOWA算子的财务管理决策法的有效性。某电力企业拟对5个备选方案作选优投资,分别是A1、A2、A3、A4、A5,为了保证决策的准确性和有效性,决策者必须客观地考虑尽可能出现的所有结果,即考虑非常好的经济形势(T1)、好的经济形势(T2)、一般的经济形势(T3)、差的经济形势(T4)、非常差的经济形势(T5)这五种情况。 步骤1三个专家进行群决策分析,每人对每一种方案根据未来可能出现的情形提出自己的观点。由于所给信息可变且模糊,因而专家们以语言信息来对方案作评,在0~8的粒度中进行评价,根据可能出现的两个标准形成二元语义评价矩阵(见表1)。按照以上方法,相应可以得出其他两个专家的评价矩阵(见表2、3)。 表1 第一个专家评价矩阵 表2 第二个专家评价矩阵 表3 第三个专家评价矩阵 步骤2通过专家对于各个方案的综合评价,将三个矩阵集结为一个评价矩阵。假设每个专家的权重为Z=(0.3,0.4,0.3),利用加权平均算法可以得到基于三个专家评价的综合评价矩阵,如表4所示。 表4 综合评价矩阵 步骤3为了更好地进行决策分析,使用诱导变量u=(13,5,8,15,7)来表达决策的精确性。诱导变量的优点在于它能够表达包括时间、压力、个人特点等相关心理方面在内的复杂的决策过程。 接下来需要确定参数β、λ和概率p。假设β=0.5,λ=2,p=(0.2,0.1,0.2,0.3,0.2)。由于未来每一种情况都有可能出现,因此对于决策来说有具有不确定性。利用OWA算子能够根据决策者的态度特征低估或高估概率结果。 步骤4将综合评价矩阵进行归一化后,相对重要性p1、p2分别为0.6和0.4,代入非线性二次偏差最优定权模型中进行最优化分析,得到权重向量为 w=(0.187,0.140,0.092,0.268,0.313) 步骤5利用2TLIGPOWA算子进行集结,结果如表5所示。 表5 各方案集结结果 由表5可知,方案排序为A3>A5>A4>A2>A1,得到第3个方案最优,即选择A3来投资。 本文主要研究了二元语义的多重属性财务掌控管理决策问题,结合研究内容提出一个新的集结算子,并探讨了它的相关性质,依据同一属性下不同方案的属性值情况建立非线性二次偏差最优权重模型。基于上述研究结果,结合决策者具备的概率特征,提出一种基于概率信息的多属性财务管理决策方法。在现实状况下,在财务掌控管理决策的过程中,决策者可以根据具体状况对算子参数作出调整,来获得一个更好的财务管理决策方案。在多属性财务管理决策问题的未来研究中,可以在模糊不确定以及区间不确定性环境下进行进一步的探讨。 参考文献: [1] Yager R R,Filev D P.Induced ordered weighted ave-raging operators [J].IEEE Transactions on Systems,Man and Cybernetics,1999(2):141-150. [2] Yager R R.Generalized OWA aggregation operators [J].Fuzzy Optimization and Decision Making,2004(3):93-107. [3] 周礼刚,陈华友,王晓,等.诱导连续区间有序加权平均算子及其在区间数群决策中的应用 [J].控制与决策,2010(2):179-184. [4] Wan S P,Feng W,Lin L L,et al.Some new genera-lized aggregation operators for triangular intuitionistic fuzzy numbers and application to multi-attribute group decision-making [J].Computers & Industrial Engineering,2016(1):286-301. [5] 谭睿璞,张文德.基于广义直觉语言算子的多属性群决策方法 [J].控制与决策,2016(11):2005-2012. [6] Merigó J M.Probabilities in the OWA operators [J].Expert Systems with Applications,2012(3):11456-11467. [7] Merigó J M,Anna M,Gil L.Induced 2-tuple linguistic generalized aggregation operators and their application in decision-making [J].Information Sciences,2013(4):1-16. [8] Merigó J M,Montserrat C,Daniel P M.Linguistic group decision-making with induced aggregation ope-rators and probabilistic information [J].Applied Soft Computing,2014(4):669-678. [9] 于超,樊治平.考虑决策者行为的新产品开发方案选择方法 [J].沈阳工业大学学报(社会科学版),2017(2):134-138. [10]Yari G,Chaji A R.Maximum Bayesian entropy me-thod for determining ordered weighted averaging opera-tor weights [J].Computers Industrial Engineering,2012(1):338-342. [11]Ahn B S.Extreme point based multi-attribute decision analysis with incomplete information [J].European Journal Operational Research,2015(3):748-755. [12]Yao O Y.Improved minimax disparity model for obtaining OWA operator weights:issue of multiple solutions [J].Information Sciences,2015(1):101-106. [13]刘培德,张新.直觉不确定语言集成算子及在群决策中的应用 [J].系统工程理论与实践,2012(4):2704-2711. [14]王中兴,刘久兵,陈晶.基于二元语言评价的群决策方法 [J].数学的实践与认识,2015(8):136-143. [15]谷云东,高建伟,刘慧晖.基于二元语义前景关联分析的风险型多准则决策方法 [J].控制与决策,2014(9):1633-1638. [16]林义征,袁宏俊,宋马林.基于相关性指标与广义IOWA算子的区间型组合预测模型 [J].统计与决策,2016(6):8-12. [17]Zeng S Z,Merigó J M,Su W H.The uncertain probabilistic OWA distance operator and its application in group decision-making [J].Applied Mathematical Modelling,2013(9):6266-6275. [18]Daniel P M.Linguistic group decision-making with induced aggregation operators and probabilistic information [J].Applied Soft Computing,2014(1):669-678. [19]Li C G,Zeng S Z,Pan T J,et al.A method based on induced aggregation operators and distance measures to multiple attribute decision-making under 2-tuple linguistic environment [J].Computer and System Sciences,2014(7):1339-1349. [20]Bapi D,Debashree G.Partitioned Bonferroni mean based on linguistic 2-tuple for dealing with multi-attribute group decision-making [J].Applied Soft Computing,2015(4):166-179. [21]文杏梓,罗新星,欧阳军林.基于决策者信任度的风险型混合多属性群决策方法 [J].控制与决策,2014(3):481-486. [22]陈华友,何迎东,周礼刚,等.广义直觉模糊交叉影响平均算子及其在多属性决策中的应用 [J].控制与决策,2014(7):1250-1256. [23]Zhou L G,Chen H Y.On compatibility of uncertain additive linguistic preference relations based on the linguistic COWA operator [J].Applied Soft Computing,2013(8):3668-3682. [24]Zhou L G,Wu J X,Chen H Y.Linguistic continuous ordered weighted distance measure and its application to multiple attributes group decision-making [J].Applied Soft Computing,2014(5):266-276. [25]刘金培,林盛,陈华友.二元语义Bonferroni集成算子及其在多属性群决策中的应用 [J].运筹与管理,2013(5):122-127. [26] Wan S P.Some hybrid geometric aggregation operators with 2-tuple linguistic information and their applications to multi-attribute group decision-making [J].International Journal of Computational Intelligence Systems,2013(4):750-763.
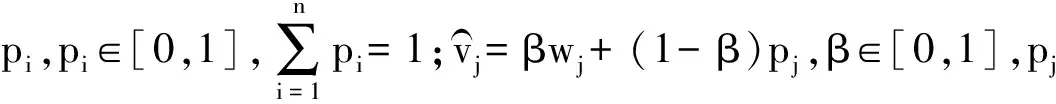
二、2TLIGPOWA算子的构建
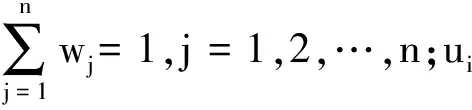
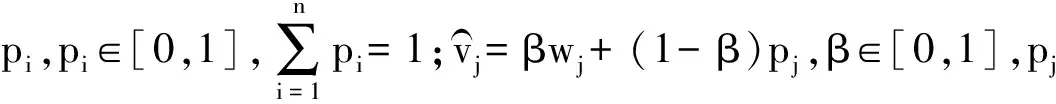
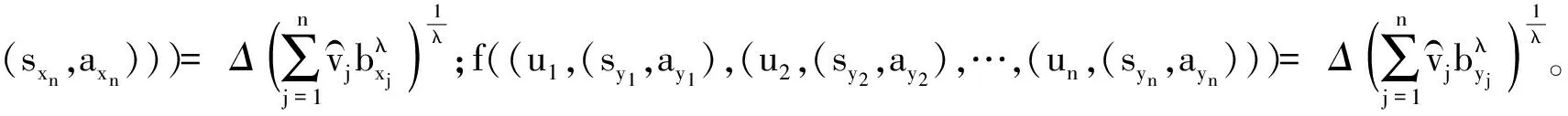
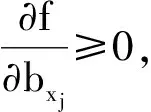

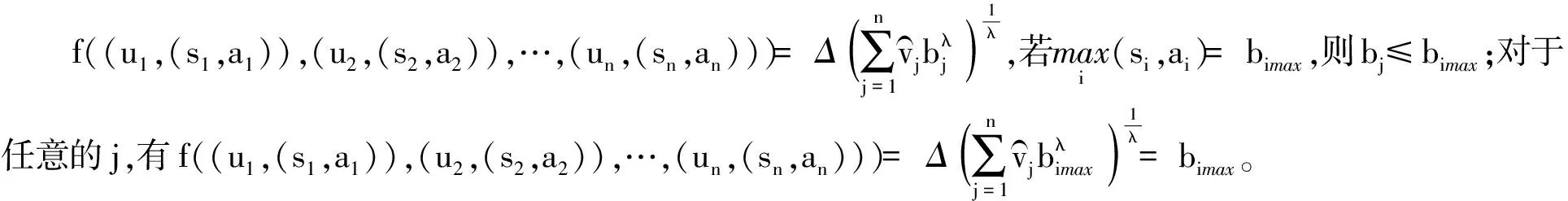
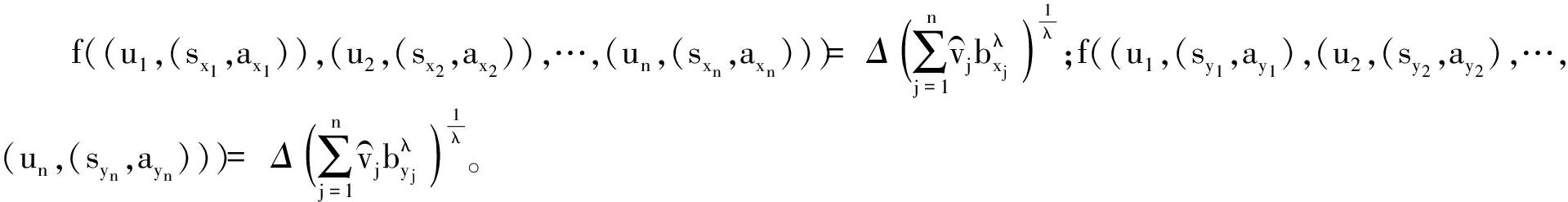
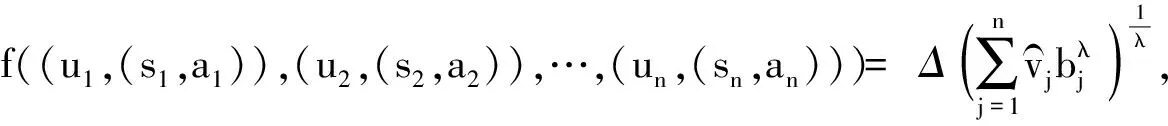
三、属性权重模型
四、基于2TLIGPOWA算子的财务管理决策方法
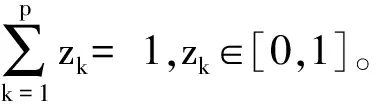

五、算例分析



六、结 论

