基于爆炸声源的水下目标定位算法
王国刚, 王洋洋, 何跃峰
(1.海军驻716研究所军代表室, 江苏 连云港 222061;2.江苏自动化研究所, 江苏 连云港 222061)
随着潜艇作战能力及隐身技术的不断发展[1],水面舰艇对潜远程预警与攻防已成为当前水下作战的重要需求[2-5]。水面舰艇主要通过舰壳声呐、拖曳线列阵声呐探测潜艇目标[6],由于其探测作用距离有限,且随着潜艇隐身能力的提升,对于较远距离目标只能通过被动声呐探测,不但不能获得有效的距离数据,而且获得的方位信息也存在较大误差,难以实现水下目标的精确定位[7-11]。
火炮发射的炮弹和飞机投射的炮弹不仅是一种优越的杀伤性武器,还是一个很好的爆炸声源[12-15]。爆炸在带来巨大破坏性的同时通常会伴随声波的产生,这种声波具有声强级高、频率低的特点,可以顺利传播到远端,起到探测远距离水下目标的作用。
本文基于爆炸声源和被动声呐探测的条件,建立一种新型水下目标定位算法实现远距离水下目标精确定位的目的,争取先敌发现、先敌攻击、先机制敌,为反潜武器系统中远程反潜提供理论支撑。
1 模型建立
基于爆炸声源的水下目标定位算法通过在预定点增加主动爆炸声源,被动声呐接收爆炸声波的直达波以及目标反射波,根据爆炸位置、回波时间间隔、目标反射波方位,利用三角定位法计算目标的距离信息,结合方位信息进行目标定位、运动要素解算。
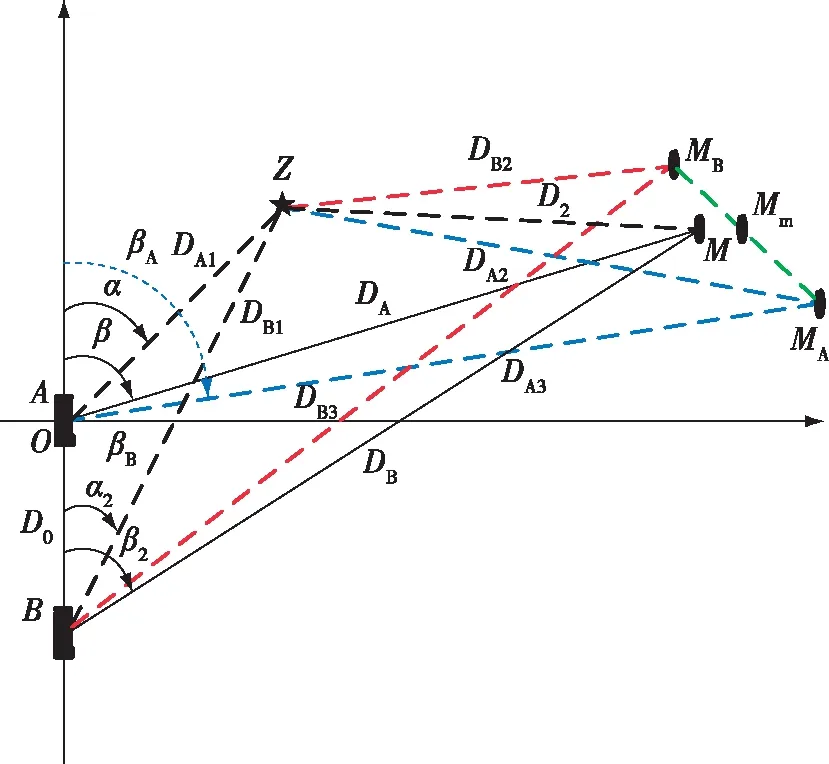
以声呐为原点O,正北方向为Y轴建立直角坐标系,设定目标B的真实方位(D3,β),设定主动爆炸点A的方位(D1,α),AB两点连线距离为D2,如图1所示。
由于被动声呐方位探测存在误差,假定实际探测方向为βm。设定ΔT为目标反射波与爆炸直达波的时间差,误差为t,如图2。暂不考虑海情对声波传播速度的影响,取定值c=1500m/s,可以得到目标探测距离为
(1)

图1 定位模型示意图

图2 声呐时域简图
误差设定:本模型暂不考虑海情对声波传播速度的影响。考虑到爆炸点的方位以及距离误差较小,且经后续仿真发现,爆炸点误差对计算结果影响很小,模型中也不再予以讨论。因此影响目标探测距离的主要误差来源于探测方位βm以及回波间隔ΔT的误差,均取决于声呐本身信号的接收、识别、处理能力。本文讨论的各项内容均假定被动声呐测向误差满足正态分布,信号识别误差不大于1s。
2 数值计算与仿真
2.1 爆炸点的选择
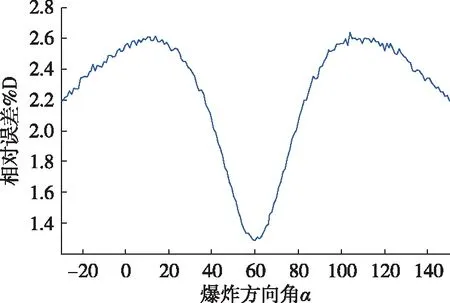
在目标探测距离的计算中,爆炸点的距离和方位是影响结果的重要因素,在考虑各项误差的条件下,寻找出最佳爆炸点减小测距误差尤为重要,本模型只考虑D1 首先研究爆炸点方向对测距误差的影响,选取最佳爆炸角度。对上述模型进行仿真计算,令目标B方位(30000m,60°),爆炸点A方位(10000m,α),水中声速梯度影响暂不考虑,声速c取1500m/s,暂不考虑爆炸点距离误差。令爆炸选取角度α由-30°顺时针旋转到150°(连线与正北方向夹角,在左为负,在右为正),统计每一个角度测距相对误差平均值。仿真结果如图3。 图3 随爆炸点方位变化误差统计(D1=10000m,D3=30000m) 由图中可见,当爆炸选取角度在60°附近,即在声呐与目标连线上时,测距误差最小为1.25%D左右。更多的仿真结果发现,落点距离D1越远时,测量误差在60°附近的优势越明显。假定D1=20000m,D3=30000m,如图4。 图4 随爆炸点方位变化误差统计图 由上述仿真可以得出结论,选取爆炸点在声呐与目标连线上时,精度最高,误差最小。 受最佳爆炸角度选取仿真结果的启发,我们继续分析了爆炸点距离D1与测距误差之间的关系。仿真发现:对于相同目标距离D3,爆炸点距离D1对测距误差影响不大。保持目标距离D3=30000m不变,改变爆炸点距离D1=2000m时,60°测距误差为1.25%D,其余爆炸角度误差普遍降低,如图5;D1=20000m时,60°测距误差为1.30%D,如图4。 图5 随爆炸点方位变化误差统计图(D1=2000m,D3=30000m) 由上述仿真结果可知,爆炸点距离D1对60°测距误差影响不大,且测距相对误差稳定于一个较小的值,对于D3=30000m,测距误差为1.25%D左右。对于未知目标的探测,更适合于选取近距离爆炸点,减小各个方向的测距误差,此时的爆炸点方位角影响较小,可任意选取。 同样,我们继续分析了目标距离D3与测距误差之间的关系。仿真发现:对于相同爆炸点距离D1,随着目标距离D3的增大,测距相对误差逐步减小,且效果明显。保持爆炸点距离D1=10000m不变,目标距离D3=40000m时,60°相对误差为0.94%D,如图6;D3=50000m时,60°相对误差为0.75%D,如图7。 图6 随爆炸点方位变化误差统计图(D1=10000m,D3=40000m) 图7 随爆炸点方位变化误差统计图(D1=10000m,D3=50000m) 爆炸产生的巨大声能可以传播到远端,但是声波的扩散和海水的吸收会逐渐消耗掉声能,为了能够探测到目标,必须保证目标反射波的声能足以被被动声呐检测到,因此借助爆炸探测存在一个最大的探测距离。假定爆炸产生的声源级为SC,若要达到探测目的,则需满足声呐方程: SC+TS-PL1-PL2-N>DT (2) 其中TS为目标强度,PL1为爆炸点到目标的传播损失,PL2为目标点到本舰的传播损失,N为噪声干扰级,DT为检测门限。 对于已被被动声呐检测到的目标,只需满足: SC-PL1>0 (3) 对于未被被动声呐检测到的目标,则需满足: SC+TS-PL1-PL2-N-DT>0 (4) 由于爆炸声为低频声波,所以吸收损失较小暂不考虑,只考虑扩展损失。则有: SC+TS-20lg[(D3-D1)·D3]-N-DT>0 (5) 推出 (6) 图8 探测区域仿真图 根据爆炸的强度以及爆炸点距离,可以计算出探测目标的区域。基于爆炸声源的水下目标定位模型的优势在于,若爆炸强度可以满足,可探测到被动声呐预警距离以外的目标,扩大了作战区域,此时可仅借用爆炸探测数据对目标进行定位。 为了更快更准地解算目标运动要素,就需要在最短时间内获得最多的数据点,因此计算出最短的爆炸间隔尤为重要。 根据上述结论,选定爆炸点为声呐与目标连线上。计算爆炸间隔的关键在于目标回波(二次回波)不可被后续爆炸的直达波覆盖。影响发射间隔的关键参数为声呐波——波分离判断时间tp,海面、海底回波和混响是影响tp的关键因素,对于海深较深海区,上述因素影响较小,将有利于波——波分离判断。假定在第一个爆炸声直达波与二次回波ΔT之间最多爆炸N次,为了避免声波覆盖以及能被声呐分离开,则爆炸间隔ts需满足ts≥(tp+tr),其中tr为容差时间,用以避免测量误差带来的时间偏移。对于连续爆炸次数需进行下列讨论: 1)仅爆炸N次: 此时仅需考虑时间间隔ts,如图9、10。 图9 爆炸N次间隔分割图 图10 爆炸N次声呐接收时域图 爆炸次数为 (7) 2)爆炸次数大于N次(第一次爆炸编号为0,N取1,2,3…): 为了避免第一个回波间隔ΔT内爆炸声目标回波被第二个ΔT内的直达波所覆盖,需要对第1、N+1次爆炸时间进行调配,如图11、12。 图11 爆炸N+次间隔分割图 图12 爆炸N+次声呐接收时域图 此时ΔT内最大爆炸次数为 (8) 具体爆炸时刻见表1。 特别注意的是,N与N+1之间相差3个ts,可看做将0与1之间的一个ts拿来所用。mN与mN+1之间以此类推,相差3个ts(m取1,2,3…)。 基于爆炸声源的水下目标定位算法即建立在上述最短发射间隔上,在最短的时间内连续产生多次爆炸声波,获取目标方位,进行目标运动要素解算。若间断爆炸,可参照表中时间,避开重叠爆炸时刻即可。 获得方位和距离信息可进行航路仿真检验算法的可靠性。 设定目标B方位(20000m,60°),航向20°匀速航行,爆炸点A方位(5000m,60°),对获得的方位、距离数据进行递进式最小二乘拟合,如图13、14。随着数据点的增多,模拟的方位和航迹逐渐逼近于真实值,可见算法本身是正确的。 图13 目标方位仿真图 图14 目标航迹仿真图 012…NN+1…爆炸时刻0ts3ts…(2N-1)·ts(2N+2)·ts…一次回波D1cD1c+tsD1c+3ts…D1c+(2N-1)·tsD1c+(2N+2)·ts…二次回波D1c+2N·tsD1c+(2N+1)·tsD1c+(2N+3)·ts…D1c+(4N-1)·tsD1c+(4N+2)·ts… 然而由于被动声呐本身的缺陷,使得探测误差太大,想要解算出航路需要大量的点,而这些点的代价是巨大的。考虑到水下目标机动性较差,攻击武器的自搜索能力较强,变航路解算为打击当前点更为合适,当然,利用编队定位优势更佳,如图15,两只相同参数声呐相距D0=4000m。仿真发现,对于上述运动要素的目标,仅需间隔3秒爆炸3次,即可使平均落点误差小于600m,如图16。 图15 编队定位模型示意图 图16 目标航迹仿真图(编队) 本文采用主动添加爆炸声源的方式建立被动声呐的水下目标定位算法,其探测距离远、精度高。仿真结果表明,当爆炸声源在目标与声呐连线上时,探测误差最小。足够大的爆炸声源级可以扩大探测区域,达到先敌发现、先敌攻击、先机制敌的目的。最短的爆炸间隔保证了在最短的作战时间内获取目标信息,实现对目标的快速定位。编队联合探测更加体现了算法的优势,在极短的时间内锁定目标、即时打击。基于爆炸声源的水下目标定位算法为现有装备配置下实现中远距离探潜、反潜提供了理论支持。 参考文献: [1]苏强,王桂波,朱鹏飞,等.国外潜艇声隐身前沿技术发展综述[J].舰船科学技术,2014,36(1):1-9. [2]吴小勇. 反潜体系的搜索能力优化方法研究[D].国防科学技术大学,2012. [3]陈虹宇,杨益新,唐建生.水声对抗方案的逐层参数优化法研究[J].兵工学报, 2012, 33(4):508-512. [4]杨日杰,熊雄,郭新奇,等.基于潜艇磁偶极子模型的航空磁探潜探测宽度模型与仿真[J].兵工学报,2014,35(9):1458-1465. [5]江传富,杨坤涛,王江安,等.机载红外热像探潜技术[J].华中科技大学学报(自然科学版),2006(7):90-92. [6]余华兵,孙长瑜,李启虎.第四讲 探潜先锋——拖曳线列阵声呐[J].物理,2006(5):420-423. [7]李关防,崔杰,袁富宇.基于线谱瞬时频率估计的被动声呐目标运动分析[J].兵工学报,2017,38(7):1395-1401. [8]余赟,赵春梅,袁延艺.舰艇声呐多阵联合被动测距技术研究[J].兵工学报,2015, 36(S2):124-132. [9]程广利,张明敏.一种度量不确定环境中被动声呐作用距离的计算方法[J].兵工学报, 2014, 35(1):140-144. [10] 郭伟. 水下监测系统中目标探测若干关键技术研究[D].国防科学技术大学,2011. [11] 生雪莉,罗方方,郭咏,等.垂直阵时反聚焦的目标被动定位方法研究[J].兵工学报,2011,32(3):359-364. [12] 金彦丰.连续爆炸式声源声源级测量方法研究[J].舰船电子工程,2016,36(2):126-128+142. [13] 周鸿涛,魏士俨,杨燕明,等.用定深爆炸声源反演海底声学参数[J].应用海洋学学报,2015,34(4):586-594. [14] 盛振新. 水下连续爆炸声学特性及信号分析研究[D].南京理工大学,2013. [15] 裴善报,刘荣忠,郭锐.水下连续爆炸声学特性分析[J].南京理工大学学报,2015,39(2):144-148.



2.2 探测距离


2.3 最短爆炸间隔


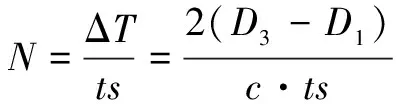


2.4 航路仿真检验




3 结束语

