基于非均匀分环与最小通信代价的路由算法*
尚 静,董增寿,康 琳
(太原科技大学电子信息工程学院,太原 030024)
无线传感器网络是由大量能量有限的传感器节点组成,并且网络一旦部署就不能人为的进行更换电池,所以能量受限是传感器网络面临的主要问题之一[1]。利用分簇路由算法可以增加网络的可扩展性和延长网络的生存周期,故得到了广泛的关注和研究。
LEACH[2]是第1个含有成簇思想的无线传感器网络路由协议。其主要思想是通过“轮”,随机循环的进行簇头的选举和簇的重构,从而将网络的能耗均衡的分配到每个节点上。LEACH能有效的提高网络的生存周期,但是LEACH也可能会造成簇头分布不均、能量空洞等问题[3-4]。文献[5]中模拟实验表明如果节点采用均匀分布策略,网络中可能有高达90%的能量被浪费。文献[6]中指出根据节点与Sink节点的距离不同,使节点担任不同的负载是解决能量空洞的一种途径,所以我们是以区域划分的形式来分析网络负载的,即引入了环状分簇的方法。
刘志[7]等人提出了分环多跳的分簇路由算法RBMC,该算法将监测区域划分为若干个均匀间隔的同心圆环,以各环簇头能耗相等为目标得到各环的最优簇头数,最终形成一个能耗均匀、簇大小异构的多跳WSN网络。虽然RBMC算法在很大程度上均衡了节点能量消耗,延长了网络的生存周期,但RBMC算法仍使用LEACH阈值公式来选择簇头,没有考虑簇头能量、地理位置等因素。针对RBMC的缺陷,Zhi Ren[8]等提出ERBMC算法,ERBMC通过在簇头选举概率公式中增加能量因素、引入了簇头多轮选择机制和提出由簇间权衡值来建立一个更加可靠的簇间多跳路由三方面的改进来提高网络的生存周期,但ERBMC算法没有解决可能会出现的簇头分布不均等问题。刘生[9]等提出虚拟分块非均匀分簇算法VBUC,该算法一方面通过对区域虚拟分块来选择簇头,另一方面在簇头选举时考虑了能量和距离因素。但VBUC算法在选择簇头和簇间多跳路由选择时,只考虑了距离因素,未考虑剩余能量的影响。Gong B[10]等提出能量异构的分簇方案EHCS,该算法通过使传感器节点的初始能量随着与Sink的距离不同而变化来避免能量空洞现象,即在不同的地理位置部署具有不同初始能量的节点。但传感器节点一般都是随机分布的,所以EHCS在现实中难以实现。Jiang J[11]等提出基于非均匀分簇算法UCRP,该算法在均匀环内分别放置3种不同能量的节点,并通过数学理论推导得到各环最优簇半径来实现能量均衡的目标,但同样在现实中难以实现。为解决簇头能耗过大的问题,文献[12]利用粒子群算法PSO选择双簇头来实现非均匀分簇,以减少主簇头能耗。文献[13]设计了基于簇头分级的非均匀分簇算法CHCI,通过为主簇头设置重选因子和次要簇头选择最佳中继路径来降低节点能耗。
本文提出的URMC算法首先通过为各环分配不同的环宽度来均衡各环的能耗;其次通过通信代价公式来选择簇头和建立簇间路由传输方式,其中通信代价公式综合考虑了距离与剩余能量因素。URMC算法避免了上述论文可能会出现的簇头分布不均、考虑因素单一、难以操作等问题,有效的延长了网络的生存周期。
本文的内容安排如下:第1节介绍网络模型,第2节详细介绍URMC算法的具体实现过程,第3节通过MATLAB仿真验证算法的优越性,第4节是结束语。
1 网络模型
1.1 系统模型
假设N个传感器节点随机分布在半径为R的圆形监测区域中,将监测区域分为若干个宽度不同的同心圆环,Sink节点位于圆心位置。如图1所示为网络的系统模型,图中将网络分为3环,由内而外分别为首环C1、第2环C2和第3环C3。R1、R2、R3分别是3个同心圆的半径,r1、r2、r3分别是各环之间的宽度。则第i个同心圆的半径Ri和环宽度ri之间的关系式为:
R1=r1
(1)
Ri=Ri-1+ri
(2)
其他有关节点的假设如下:①所有节点(包括Sink节点)一旦部署就不再变化,即所有节点都是静止的;②所有节点的初始能量都相同;③所有节点都没有位置感知功能,可以通过接收消息的强度值RSSI来计算与消息发送者的距离;④传感器节点的能量是有限的,而Sink节点的能量是无限的或是可以补充的;⑤每个节点都有不同的ID号。

图1 系统模型
1.2 能耗模型
本文采用与文献[7]相同的能耗模型,如图2所示为能耗模型图。

图2 网络能耗模型
如图2所示,当节点Si将Lbits数据包发送到距离为d的节点Sj时,节点Si发送能耗ETx(l,d)为:
(3)
节点Sj的接收能耗ERx(l)为:
ERx(l)=lEelec
(4)
当数据的相关性较强时,节点首先对数据进行融合,再发送出去。融合能耗EDA(l)为:
EDA(l)=lEelec
(5)
式中:Eelec为接收或发送1bit数据时的能耗,εfs、εmp分别为自由空间模型衰减系数和多径衰减系数,d0为距离阈值。d0表达式如下:
(6)
2 URMC算法描述
2.1 首环半径
采用簇间多跳路由传输方式时,靠近Sink的节点转发任务重,负载大,容易过早死亡。所以在此第1环的节点直接向Sink节点发送感知到的数据,而不经过簇头的转发,即第1环的簇头只起到转发外环簇头数据的作用。
假设节点Si是首环簇成员节点,且节点Si到Sink节点的距离dtoSink (7) 当节点Si经过簇头CHi转发给Sink节点时,假设节点Si到簇头CHi的距离dtoCH (8) 式中:α为融合系数。 本文中所提到的融合均为完全融合方式,即每个簇头将自身簇成员节点的数据接收并融合成1单位的数据包向外传送,所以融合系数α的表达式为: α=1/Nc (9) 式中:Nc为每簇的节点数。由于α很小,故将Eforward省略为: (10) 当EtoSink≤Eforward时,节点Si选择直接发送给Sink节点更节能,此时dtoSink需要满足的条件为: (11) (12) 式中:m1为首环簇头个数,r1为首环半径。将式(12)代入式(11),可得: (13) 解得首环半径r1应满足: (14) 综上理论分析,当首环半径r1满足式(14)时,首环簇成员节点将数据直接发送给Sink节点更加节能。所以本文利用式(14)可求得首环半径r1的值。 无线传感器网络分簇路由所形成的簇结构需要包含网络中所有的节点,并且每个簇中只有一个簇头节点和若干个簇成员节点。如图3所示,当簇与簇之间的重叠最多时,簇头数最大;反之,如图4所示,当簇与簇之间的重叠最少时,簇头数最小。 图3 最大簇头数 图4 最小簇头数 根据文献[10]中Gong B得出最大簇头数与最小簇头数的表达式,即若环Ci的面积为Si,且簇半径为rc时,环Ci内最大簇头数mmax为: (15) 最小簇头数mmin为: (16) 本文中,我们假设环Ci中簇半径均为ri,即环Ci的宽度。故环Ci中期望的簇头数为: (17) 由于首环簇头负载较重,能耗较大,所以我们为其分配较多的簇头数,即首环的簇头数m1为式(18)所示,其余各环的簇头数均为式(17)所示的mi。 (18) 本节首先计算各环中节点的能耗,其次通过各环能耗均等为目标推出各环最优环宽度的表达式。 在每个簇头周期中,簇头能耗主要分为两部分,一部分为接收、融合和发送自身簇成员的数据,我们称之为本地能耗;另一部分为接收和发送外层簇头的数据,我们称之为转发能耗。由于各环之间的数据相关性较小,所以对不同环的数据不进行融合,以此来节约能量。 假设将圆形区域分为S个非均匀圆环,则第i环节点数Ni为: (19) 式中:ρ为网络中的节点分布密度。 (20) 第i环中簇头到Sink的距离的期望E[dCHi]为: (21) (22) 当i=1时,即首环节点能耗公式计算如下: 首环簇成员节点直接将数据发送给Sink节点,不需要经过簇头的转发。所以首环节点的能耗Etotal1为: (23) (24) 将式(25)代入式(23)得: (25) 当i>1时,第i环节点的能耗计算如下: (26) 式中:ρ(r,θ)为第i环中簇头密度,r为簇成员节点与簇头之间的最远距离,即簇半径。具体计算如下: (27) (28) (29) 代入上式可得: (30) 第i环中每个簇头的本地能耗ECHlocal和转发能耗ECHforward分别为: (31) (32) 第i环中每个簇成员节点的能耗ECM为: ECM=ETx(L,dCMi) (33) 则第i环中一个簇的能耗Ecluster为: (34) 第i环中节点的能耗Etotali为: Etotali=miEcluster (35) 由于簇成员与簇头之间的距离dCMi比较小,所以我们假设dCMi ①当dCMi (36) ②当dCMi (37) 综上,当i>1时,第i环节点的能耗与第i环节点数Ni、簇头数mi、簇头与簇头之间的距离dCHi,i-1、簇成员节点与簇头之间的距离dCMi有关,而这些因素均只与环宽度ri有关,故第i环节点的能耗只与环宽度ri有关。 根据各环能耗均衡准则,即式(37),可得到各环宽度之间的关系。 Etotali=Etotali-1=…=Etotal1 (38) 网络部署结束后,Sink节点向外广播Sink-notify消息通知所有节点开始工作,并且每个节点通过计算RSSI值得到与Sink的距离,从而确定自己所属环数。 URMC采用和VBUC算法相同的方法来选择候选簇头,然后通过计算在不同区域编号中每个候选簇头的通信代价值,最终选择通信代价值最小的候选簇头作为该区域编号的最终簇头。 假设S(c)为区域编号k中所有候选簇头的集合,则区域编号k的最终簇头CH(k)由下列等式进行选择: CH(k)=CHj (39) CHj=argmin{cost(i),i∈S(c)} (40) (41) 式中:∑d(w,i)表示区域编号k中其他所有节点与候选簇头i的距离之和,nk表示区域编号k中节点个数,d(i,Sink)表示候选簇头i与Sink节点的距离,E(i)表示候选簇头i的剩余能量,α、β、γ分别为各个影响因素的加权因子。 由于簇头在簇内通信时,其他节点与其的距离为影响能耗的主要因素,簇头的能量为次要因素,与Sink节点的距离为最小因素,所以分配值分别为:α=0.5、β=0.2、γ=0.3。 当选为最终簇头的节点向外广播CH_NOTIFY消息,消息包括节点ID、节点与Sink的距离、节点当前轮剩余能量。非簇头节点通过计算接收到CH_NOTIFY消息强度值,选择距离自己最近的簇头作为自身簇头,簇建立阶段完成。 假设S(CHi-1)为第i-1环所有簇头节点的集合,则第i环中簇头CHi的下一跳簇头节点Next(CHi)由下列等式进行选择: (42) CHc=argmin{cost(CHf),CHf∈S(CHi-1)} (43) (44) 式中:d(CHi,CHf)为相邻环两个簇头之间的距离,d(CHf,Sink)为簇头CHf与Sink之间的距离,E(CHf)为簇头CHf的剩余能量。在簇间路由传输时,簇头与簇头之间的距离为影响能耗的主要因素,簇头的能量为次要因素,簇头与Sink的距离为最小因素,所以分配加权因子分别为:α=0.5、β=0.2、γ=0.3。 第i环中簇头CHi通过计算第i-1环中每个簇头的通信代价值,选择最小通信代价值的节点作为簇间路由传输的下一跳,从而簇间路由建立阶段完成。 本节利用MATLAB仿真平台对提出的算法URMC与LEACH、RBMC、VBUC算法进行性能比较。 假设监测区域R=180 m总分环数S=3;根据式(17)、式(18)和式(38),可得到各环簇头数和宽度:m1=4、m2=16、m3=11、r1=81 m、r2=30 m、r3=69 m。其余仿真参数如表1所示。 表1 仿真参数 3.2.1 簇头分布图 如图5所示,分别为LEACH、RBMC、VBUC及本文URMC算法的簇头分布图。 由于LEACH算法和RBMC算法随机循环的进行簇头选举,所以会造成簇头分布不均的情况;VBUC算法是在RBMC算法的基础上每环根据最优簇头数进行虚拟分区,簇头在虚拟小区内进行选取,有效的改善了簇头分布不均的情况,但VBUC算法无法确保在算法运行过程中每环的簇头分布与理论得到的最优簇头数一致,如图首环的簇头数为4,但根据理论计算得到的值为5;URMC算法对圆形区域进行非均匀分环,并在VBUC算法的基础上对其调整,所以既提高了簇头分布的均匀性,又保证了各环簇头数与理论值一致。 图5 4种算法的簇头分布图 图6 网络的生存节点数 3.2.2 网络生存周期 在此定义50%节点死亡的轮数为网络的生命周期。如图6及表2所示,由于LEACH算法可能会出现能量较小的节点当选簇头或者出现能量空洞现象,所以LEACH算法只运行到604轮时网络生命周期就结束;RBMC算法在LEACH的基础上对不同区域分配不同的簇头概率来克服能量空洞现象,将网络生命周期延长到了1 583轮;VBUC算法在RBMC基础上对区域虚拟分区来提高簇头分布的均匀性,将网络生命周期延长到了1 730轮;本文的URMC算法既通过非均匀分环来克服能量空洞现象又比VBUC算法增加了能量因素,所以URMC算法将网络生命周期延长到了2 006轮。 表2 死亡节点轮数比较 如图7所示为基于最小通信值的簇头选择和簇间路由树算法下,非均匀分环与均匀分环的生存节点数对比。从图中可看出,随着网络运行时间的增长,节点的剩余能量越低,非均匀分环相比较于均匀分环网络的生存节点数较多,性能较好。 图7 非均匀分环与均匀分环 3.2.3 节点平均剩余能量 如图8所示,由于URMC算法综合考虑了节点的能量和距离,所以较其他3种算法节点平均剩余能量下降较缓慢。 图8 节点平均剩余能量 本文提出了一种基于非均匀分环与最小通信代价的路由算法URMC,该算法通过非均匀分环来均衡节点负载,避免能量空洞现象,且综合考虑能量和距离因素选择簇头和建立簇间路由树。经仿真验证,URMC算法的网络生存周期较LEACH、RBMC及VBUC算法分别提高了232%、26.7%和15.9%。 [1] Kumar D. Performance Analysis of Energy Efficient Clustering Protocols for Maximising Lifetime of Wireless Sensor Networks[J]. Iet Wireless Sensor Systems,2013,4(1):9-16. [2] Heinzelman W B,Chandrakasan A P,Balakrishnan H. An Application Specific Protocol Architecture for Wireless Microsensor Networks[C]//IEEE Transactions on Wireless Communication. 2002:660-670. [3] Abo-Zahhad M,Ahmed S M,Sabor N,et al. Mobile Sink-Based Adaptive Immune Energy-Efficient Clustering Protocol for Improving the Lifetime and Stability Period of Wireless Sensor Networks[J]. IEEE Sensors Journal,2015,15(8):4576-4586. [4] Ren J,Zhang Y,Zhang K,et al. Lifetime and Energy Hole Evolution Analysis in Data-Gathering Wireless Sensor Networks[J]. IEEE Transactions on Industrial Informatics,2016,12(2):788-800. [5] Yuan H,Yang S,Xie J. Prolonging the Lifetime of Sensor Networks Using Non-Uniform Sensor Distribution[C]//Conference Anthology,IEEE. IEEE,2013:1-4. [6] Olariu S,Stojmenovic I. Design Guidelines for Maximizing Lifetime and Avoiding Energy Holes in Sensor Networks with Uniform Distribution and Uniform Reporting[C]//INFOCOM 2006. 25th IEEE International Conference on Computer Communications. Proceedings. IEEE,2006:1-12. [7] 刘志,裘正定. 基于分环多跳的无线传感网分簇路由算法[J]. 通信学报,2008,29(3):104-113. [8] Ren Z,Chen Y,Yao Y,et al. Energy-Efficient Ring-Based Multi-Hop Clustering Routing for WSNs[C]//Fifth International Symposium on Computational Intelligence and Design. IEEE Computer Society,2012:14-17. [8] 刘生. 无线传感器网络分簇路由算法研究[D]. 北京:华北电力大学,2012. [9] Gong B,Jiang T,Xu S,et al. An Energy-Heterogeneous Clustering Scheme to Avoid Energy Holes in Wireless Sensor Networks[J]. International Journal of Distributed Sensor Networks,2013,10(22):1380-1383. [10] Jiang J,Han G,Liu L,et al. An Unequal Cluster-Based Routing Protocol for Wireless Heterogeneous Sensor Networks[J]. Journal of Internet Technology,2015,16(6):945-955. [11] 门顺治,孙顺远,徐保国. 基于PSO的无线传感器网络非均匀分簇双簇头路由算法[J]. 传感技术学报,2014,27(9):1281-1286. [12] 康琳,董增寿. 基于簇头分级的改进非均匀分簇算法[J]. 传感技术学报,2015(12):1841-1845.
2.2 各环簇头数



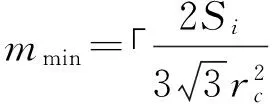

2.3 各环环宽度





2.4 簇形成阶段
2.5 建立簇间路由树

3 仿真结果分析
3.1 仿真参数

3.2 仿真结果分析





4 结束语

