基于车载传感信息融合的电动汽车驾驶行为辨识*

陶红兴,莫凌飞,严如强

(东南大学仪器科学与工程学院,南京 210096)

汽车发展至今,已经有较为成熟的生产技术,但其排放出的尾气给人们的生活,生产都带来了负面影响,因此,电动汽车的发展也被推上日程[1]。从目前的开发进度来看,电动汽车技术已经得到了长足的发展,有望在未来大量生产,或将取代传统内燃机汽车成为人们日常生活中交通的首选[2]。而随着电动汽车数目的增多,电动汽车的驾驶行为分析也就显得尤为重要,准确的驾驶行为辨识结果可以有效的监督驾驶员的行为规范,以此增加电动汽车驾驶过程中的安全性。

近年来,许多研究人员希望能够对车辆驾驶状态进行准确的辨识。研究一般分为两个方向:基于驾驶员的驾驶行为分析,或是基于车辆的驾驶行为分析。ChiyomiMiyajima,Yoshihiro Nishiwaki 和 Koji Ozawa 针对不同驾驶员的油门刹车踏板的操纵情况进行建模,并提出了一种混合高斯算法,并得到大概80%的准确率[3]。同时一些学者希望通过智能手机的传感信号来对驾驶行为进行识别,李伟健[4]等人就通过手机中的加速度传感器的变化程度识别车辆是否发生事故[5]。虽然两种研究方向都能够对驾驶行为进行分类,但是精度不高,本文希望能够基于信息融合的方法将两种信息结合起来,以提高对驾驶行为辨识的精度。

本文的目的在于提高识别电动汽车驾驶行为的正确率,主要工作有:①通过加速度传感器获得驾驶过程中的加速度数据,并通过MMA(多尺度多重分形)算法对加速度信息进行处理,提取特征值。MMA算法是一种时域信号处理方法,可以反映出加速度信号的波动情况。②通过CAN分析仪对电动汽车的OBD信息进行采集,并采用其中的速度、功率、电流等一些能够反映电动汽车驾驶行为特性的信息进行特征提取。③采用随机森林的方法对提取的特征进行有效的分类。本文中,主要对驾驶行为分为以下7个类别:加速、减速、左转弯、右转弯、左变道、右变道、正常驾驶。④提出一种信息融合方法以提高分类准确性。

1 MMA方法

MMA(Multiscale Multifractal Analysis)算法是一种处理时域信号的方法。实际上是标准多重分析算法加入了尺度因素[6]。通过MMA算法分析可以分析得到信号的波动特性以及其稳定性。该算法得到的结果是Hurst表面h(q,s),用于描述Hurst指数在不同参数q(波动阶数)和参数s(尺度)情况下波动情况的变化幅度[7]。但是实际上该方法一直没有用于特征提取,本文采用该方法,选择其Hurst指数序列作为提取的特征。其方法步骤如下所示:

①求“轮廓信号”:

(1)

②将序列Y分为Ns≡int(N/s)个连续、不重叠,且长度为s的等长子区间Vj(j=1,2,…,Ns)。实际上序列不一定完全被s整除,最后序列可能会剩余一些尾部的数据,为了充分利用数据,从Y序列的两端(首尾两端)分别切割,得到2Ns个区间。

③用最小二乘估计算法计算每个子区间的趋势,然后可以计算得到方差:

对于子区间v=1,…,Ns:

(2)

对于子区间ν=Ns+1,…,2Ns,

(3)

yv(i)是每个子区间的拟合多项式:

yv(i)=aj0+aj1i+…+ajm-1im-1+ajmim,m=1,2,…

(4)

这里m是拟合多项式的回归阶数。

④计算每个区间的q阶波动函数:

(5)

F(q,s)曲线可以反映出波动水平的大小,其中,q表示波动阶数,q为正值时,表示对数据大的波动进行分析,而q为负值时,表示对数据的小的波动进行分析。通常q取值范围为[-5,5]。

尺度值s的选择是至关重要的,MMA中采用一个移动拟合窗口,将窗口中准连续变化的s值代入到F(q,s)的运算中。假设一个拟合窗口Ri(i=1,2,…,n),而hRi对应着在Ri中计算得到的h值。然后可以计算得到每个拟合窗口的h值,h(s)={hR1,hR2,…,hRn},对于固定的q值,可以得到相对一定范围s,准连续变化的h(q)的值。对于不同的q值重复以上操作,就可以得到广义的Hurst表面[8]。h(q,s)可以通过如下公式得到:

(6)

这里F(q,s)Ri和sRi表示Ri窗口下的值。

并且所得到的Hurst指数还具有一定的物理意义:h∈(0,0.5)说明该时域信号具有一定的反持续性,h=0.5表示该信号是不相关的噪声,h∈(0.5,1)表示信号是持续性的,h=1.5说明该物体在做布朗运动,h>2则说明是黑噪声[9]。

通过MMA算法可以得到信号细致的波动情况,可以反映出不同信号的差异性。将h(q,s)值按q和s从小到大的顺序排列,得到一组序列,该序列可作为一个样本的特征序列(每个h作为一个特征值)。本文采用该方法对加速度信息进行特征提取。

2 RF方法

随机森林是一种基于决策树的集成方法,可以用于分类,回归和其他集成学习。随机森林的最小决策单元是随机决策树[10],它通过在训练期间构建出多个决策树,并以此得到多个输出分类结果的模式,最终由多个决策树进行综合投票决定输出结果。

形成随机森林基本分类器的基本步骤如下:

①通过自助(bootstrap)重采样技术,从原始训练样本集N中有放回的重复抽取k个样本生成新的训练样本集合。

②随机选取属性集合,最终形成新的样本集合。每个决策树都会得到一个结果。

③随机森林实际上就是基于多数分类投票,通过对每个决策树的分类结果投票得到最终的分类结果[11]。

3 信息融合方法

驾驶行为分析过程中,由于运行情况众多,监测量与驾驶行为之间是一种非线性映射。而且,采用单一的特征参数已经不能满足对精度的需求。解决的方案就是采用信息融合技术对多种信息进行融合,即从多个方面对驾驶行为进行描述,可以得到更多有用的信息,实现更准确的驾驶行为辨识。

信息融合方法一般分为3大类:数据层融合、特征层融合和决策层融合[12]。本文采用的是决策层融合,如图1所示。

图1 决策层融合结构

本文中,选取随机森林作为分类器,随机森林算法是通过对多个决策树进行统计得票得到最终的结果,这里将每个样本的准确度h(p|x)作为置信度,随机森林算法实际上是有多个决策树构成,对于每个样本不同的决策树有不同判定结果,这里的准确度是指这些决策树的分类的准确度。同时对于两个信息来源的分类器可以得到其准确率W作为分类器的权重,将两者的乘积作为加权投票的权重。本文中的融合算法如图2所示。

图2 融合算法结构

4 实验数据采集系统

本文中用于识别电动汽车驾驶状态的数据主要来源于两个方面:一是外加三轴加速度计,通过该模块能够收集到电动汽车在运行状态下的X、Y和Z轴方向上的加速度信息,反映电动汽车在各个方向上的运动变化情况。二是OBD信息,通过CAN分析仪,对电动汽车OBD接口上传出来的OBD信息进行解析以此得到电动汽车内部的信息:车速,电机功率,电流,加速踏板和减速踏板的相关信息。

图3(左)是本文用于采集加速度信息的arduino加速度模块,本实验中,将其水平固定于汽车上,可以得到较为真实的三轴加速度信息,其中X轴正方向为电动汽车前进方向,Y轴正方向为电动汽车的左侧,Z轴的正方形为电动汽车的垂直上方。而CAN分析仪则通过OBD接头连接CAN分析仪和OBD接口,解析CAN报文得到OBD信息,两者通过USB与上位机通讯,在本次实验中上位机采用Labview进行设计。

图3 三轴加速度计采集模块和CAN分析仪

5 实验结果及分析

5.1 实验流程

实验主要包含三部分内容:一是基于加速度信息的电动汽车驾驶行为辨识;二是基于OBD信息的电动汽车驾驶行为辨识;三是基于加速度和OBD信息融合的电动汽车驾驶行为辨识。

实验过程中统一取5 s作为数据采集的时间窗口,每种驾驶行为各测得50组样本,每组数据样本1 500点,其中30组样本用于训练,20组样本用于测试,最终实验步骤如下:①单独使用加速度信息作为信息来源,采用MMA算法提取特征后,由随机森林分类器得到分类结果。②单独使用OBD信息作为信息来源,提取特征值后,由随机森林分类器得到分类结果。③采用信息融合技术,将两种信息综合起来,由随机森林分类器得到分类结果。

5.2 基于MMA算法的加速度信息处理

在本文中,首先对电动汽车驾驶过程中的加速度信息进行处理和分类,通过随机森林算法得到它对驾驶状态的识别能力。在本次实验中,将驾驶行为分为加速,减速,左转弯,右转弯,左变道,右变道和正常行驶七大类。其中,加速,左转,左变道和正常行驶的加速度信息如下:

由图4可以看出在加速过程中,X轴加速度先由0加速到一个稳定值,具有较为明显的变化。

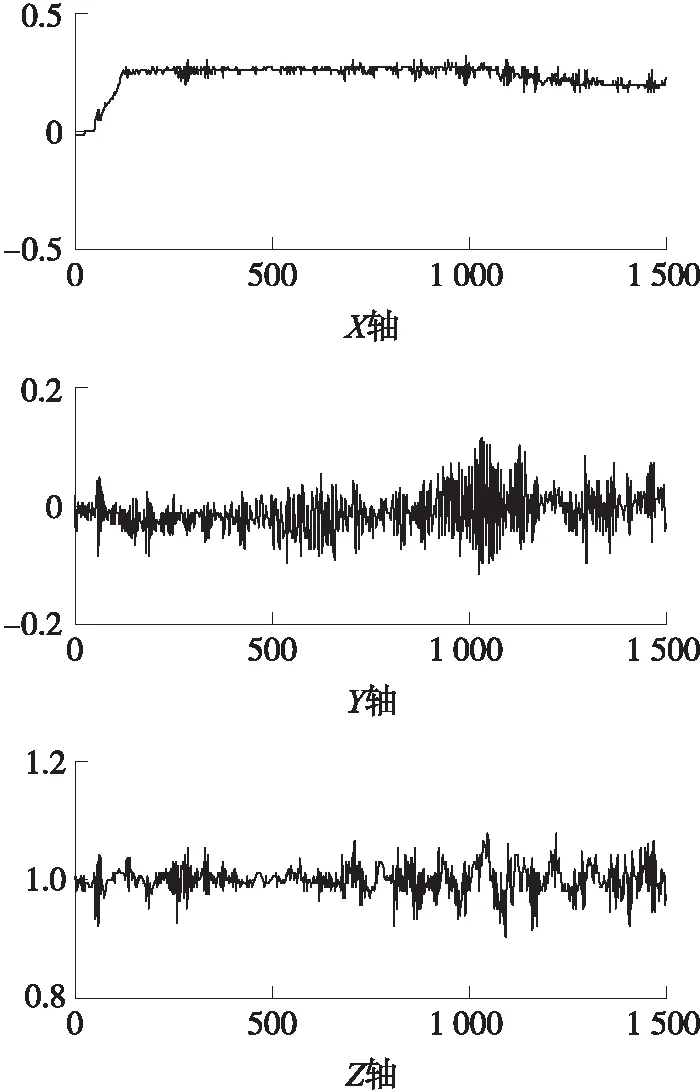
图4 加速时三轴加速度

由图5可以看出在左转弯过程中,Y轴加速度从0增加到一个稳定值后减少为0,具有较为明显的变化。

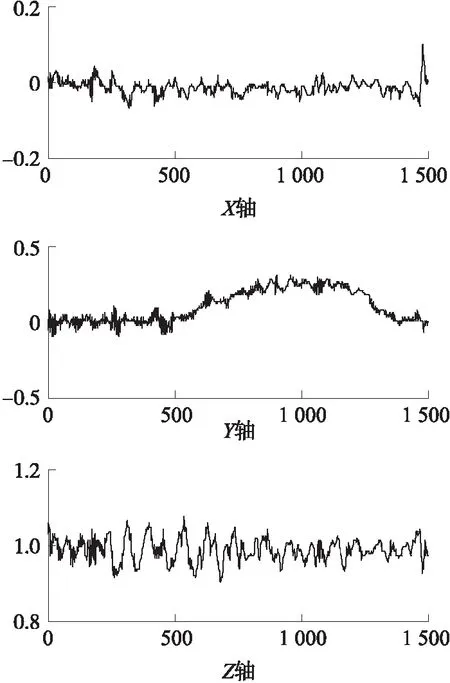
图5 左转弯时三轴加速度

由图6可以看出左变道过程中,Y轴加速度从0增加到一个值后减少到一个负值后归0,具有较为明显的变化。

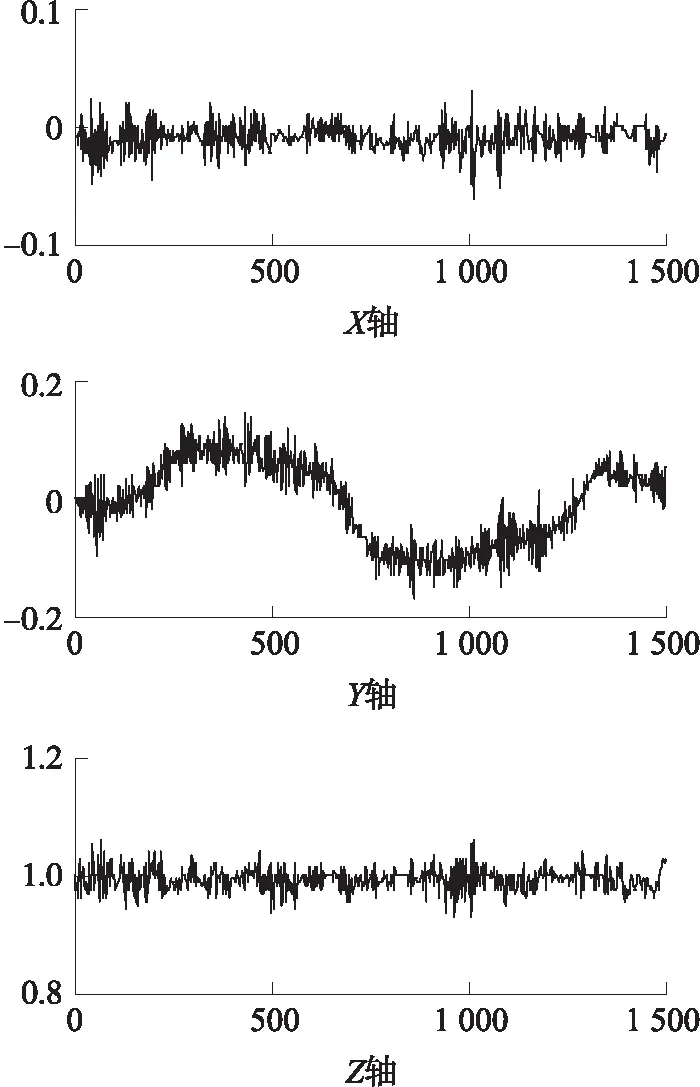
图6 左变道时三轴加速度图

由图7显示了正常驾驶过程中,三轴加速度的加速度值的变化并没有较为明显的变化。

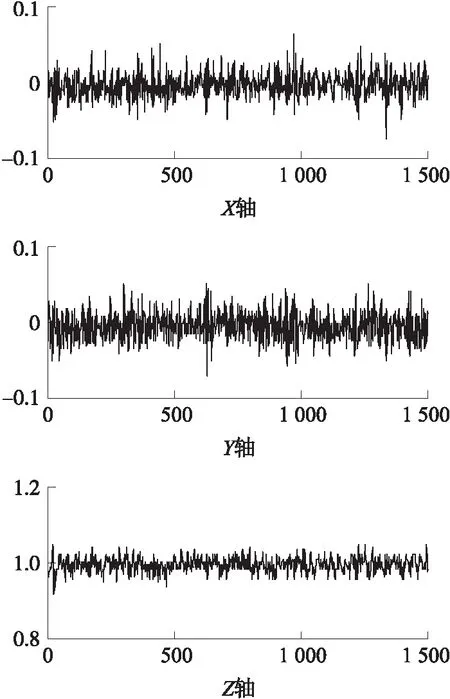
图7 正常驾驶时三轴加速度

从上图可以看出,电动汽车的7种驾驶状态在X和Y轴上加速度变化较为明显。因此,本文中采用MMA算法对原始的X和Y轴加速度信号进行处理后,得到加速度信号的波动情况,通过该算法可以得到h(q,s)图,如下所示。

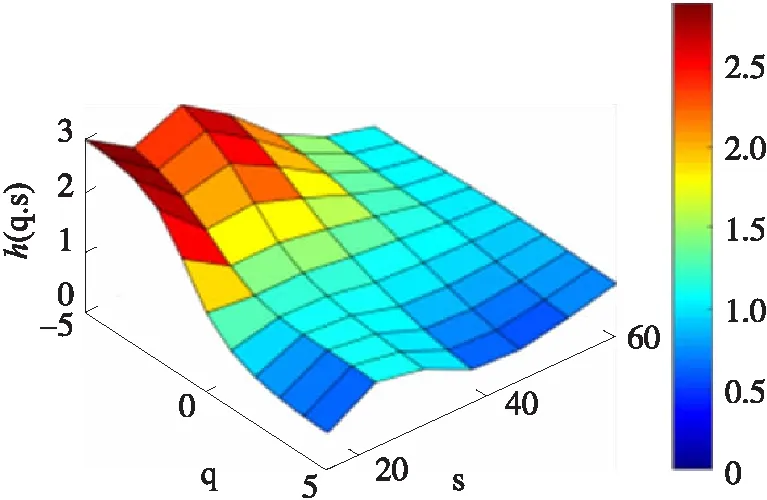
图8 加速时X轴h(q,s)

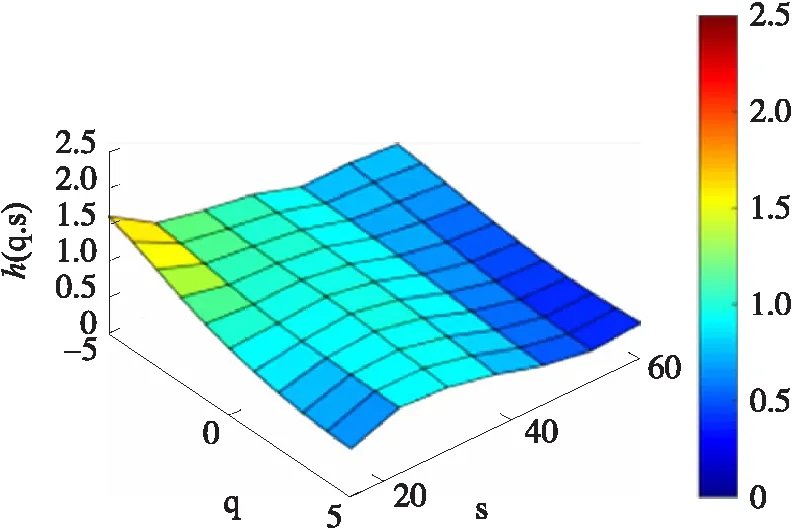
图9 加速时Y轴h(q,s)

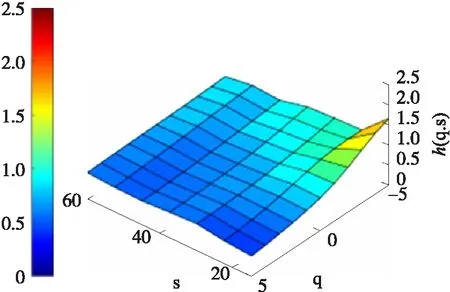
图10 左转弯时X轴h(q,s)

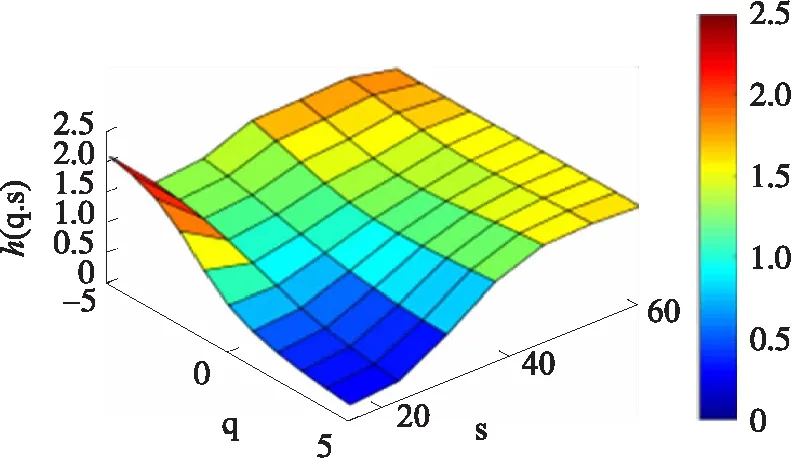
图11 左转弯时Y轴h(q,s)

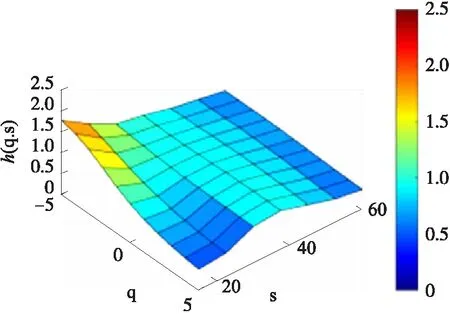
图12 左变道时X轴h(q,s)

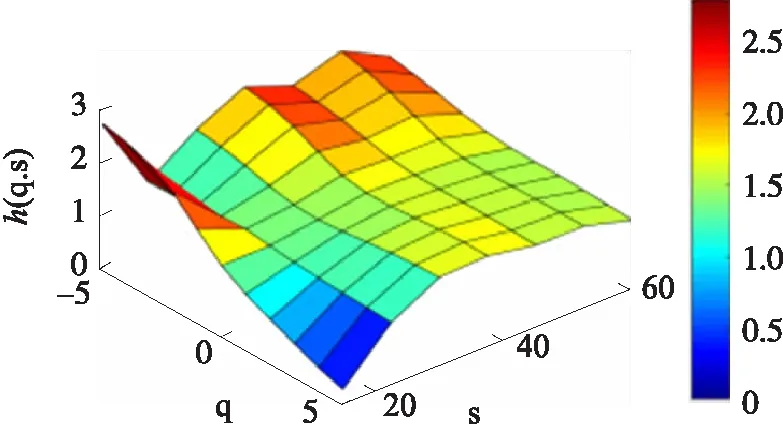
图13 左变道时Y轴h(q,s)

由于7种驾驶状态在X轴和Y轴上信号的区分度较为明显,这里展示了在加速、左转弯和左变道情况下X和Y轴加速度数据经MMA算法得到的h(q,s)图像:

在处于加速状态下,X轴的加速度变化较为明显,图像中有一较大的变化。而Y轴则相对平稳。

在处于左转弯和左变道情况下,X轴的变化较小,而从图中可以看出,两者通过Y轴加速度信息得到的图像也有较大不同,与左转弯相比,左变道的图像变化要多一个波峰,这与实际情况也相符。

由上图可以得出结论,通过MMA算法得到的h(q,s)能有效的区分出不同状态的驾驶行为,可以作为有效的特征提取方法。这里将h(q,s)按照q,s从小到大的顺序排列,得到一个Hurst指数序列,以此作为所需要的特征向量,用于随机森林分类器的训练和测试。

最终得到的分类结果如表1所示。

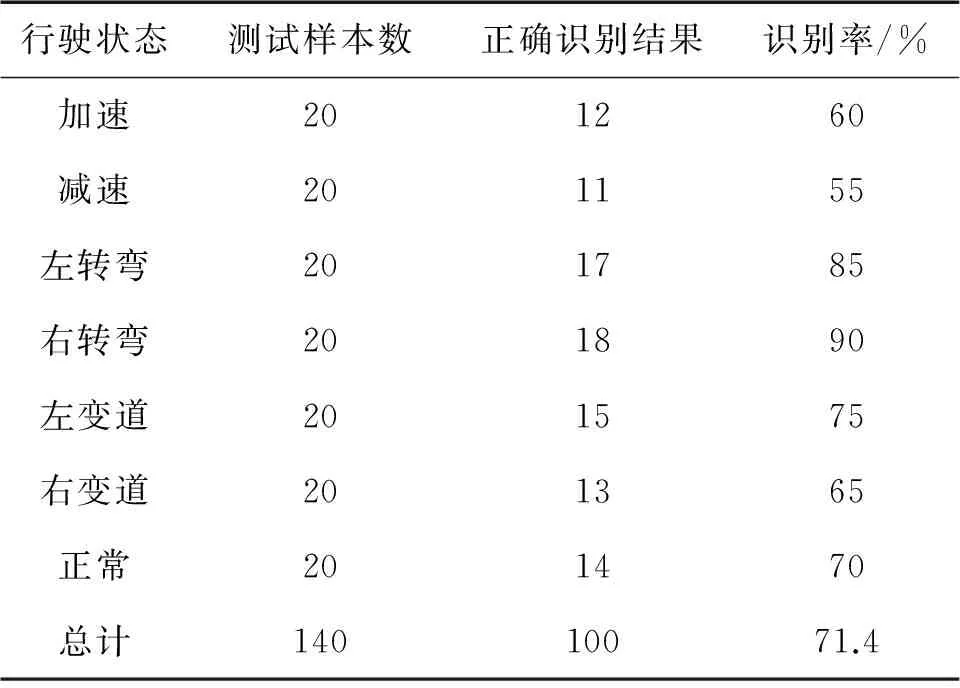
表1 基于MMA算法的加速度信息识别结果(基于随机森林)

从表1的结果可以看出通过MMA方法对加速度信号进行特征提取,并通过随机森林(RF)分类的方法可以对电动汽车的驾驶状态进行较为有效的识别。但是精度并不能达到预期的标准。

5.3 基于加速度和OBD信息融合的驾驶状态识别

电动汽车的OBD信息中包含了电动汽车的车速、电动机转速、输出电流、电机控制器温度、总电压、电池点量等相关信息,从中选取车速、电动机转速和输出电流作为信息来源。其中,加速,左转,左变道和正常行驶情况下三者的变化曲线如图所示。

图14可以看出,在加速过程中,速度、电动机转速和输出电流有着明显的增加的过程。

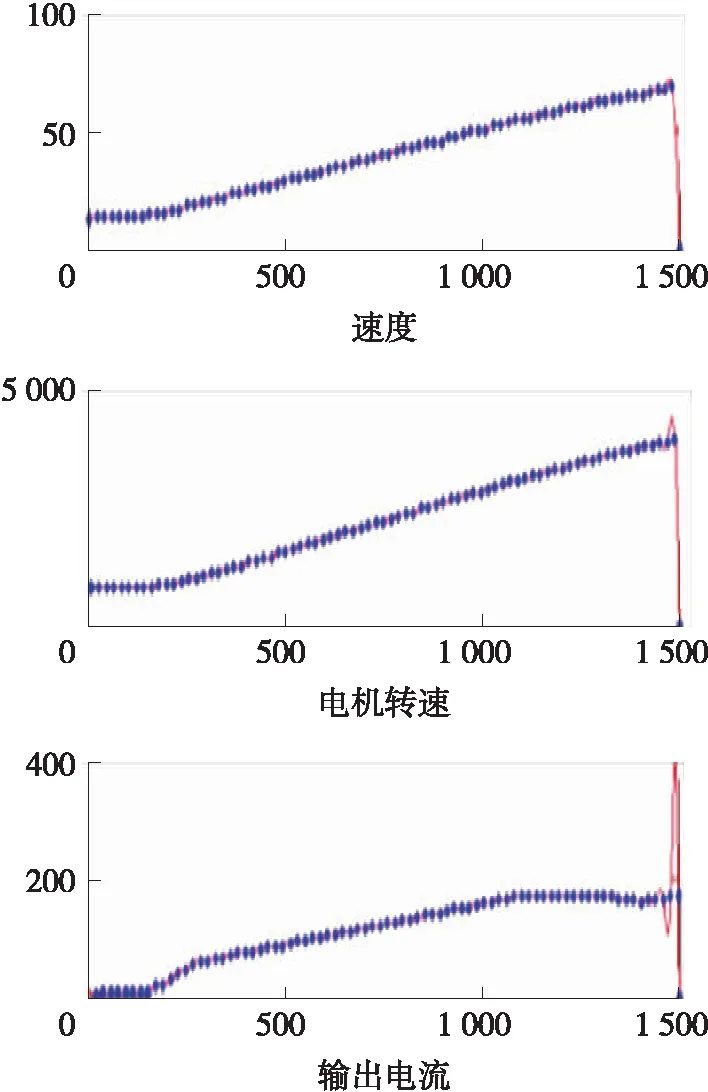
图14 加速时OBD信息

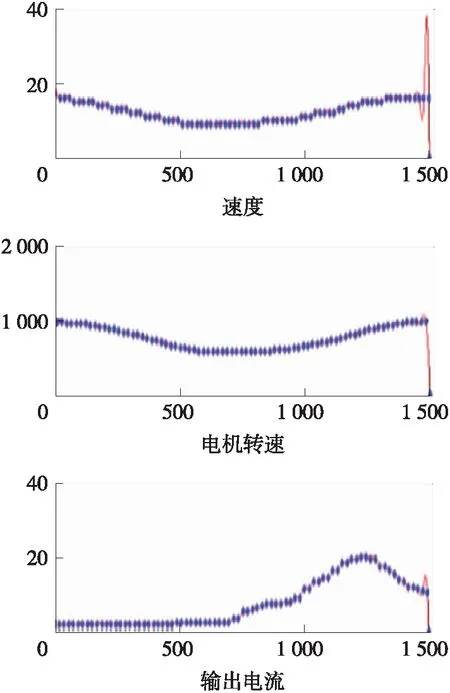
图15 左转弯时OBD信息

图15可以看出,在左转弯的过程中,速度上无明显变化,而电动机转速有较为明显的减少增加的过程。输出电流与Y轴加速度相似,有着先增加后减少的过程。

图16可以看出,在变道过程中,速度无明显变化,电动机转速有明显的减少后有稍许增加,而输出电流与Y轴加速度特征相似,先增加到一个值后减少到一个值,最后回复到稳定值。

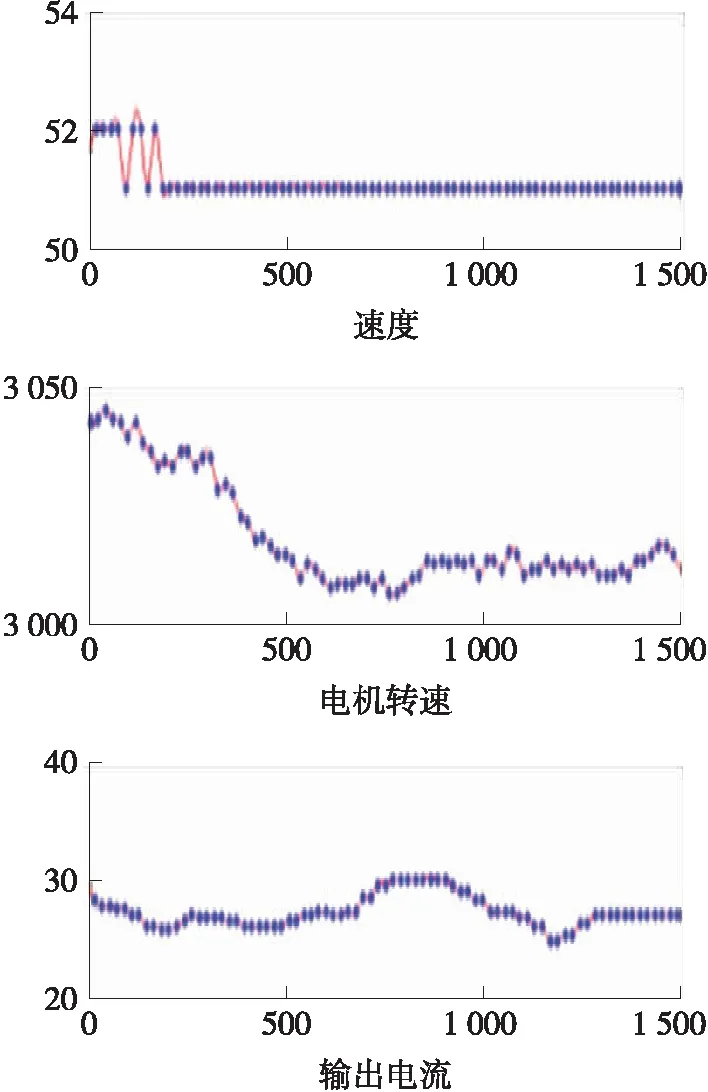
图16 左变道时OBD信息

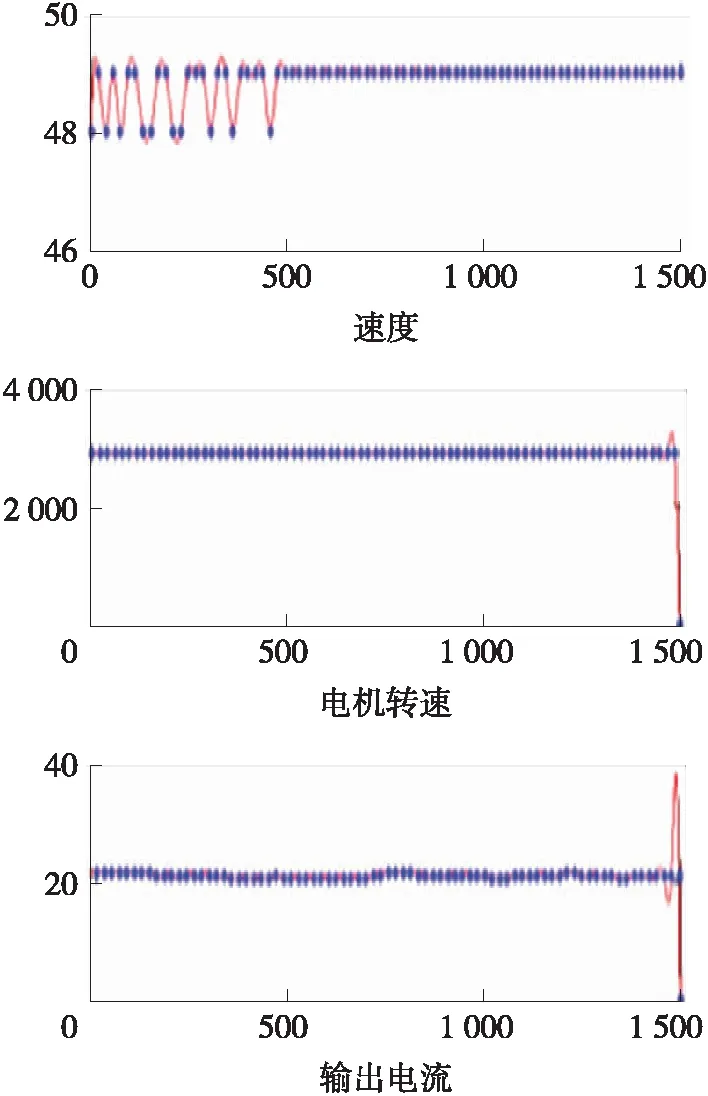
图17 正常时OBD信息

图17可以看出,在正常形势状态,速度,电机转速和输出电流均没有明显变化。

综上所述,速度、电机转速和输出电流对于不同的驾驶行为有较强的区分能力,在这里,提取三者的均值、方差、最大值和最小值作为信号的特征,将其作为输入,输入到随机森林分类器当中。得到的分类结果如下。

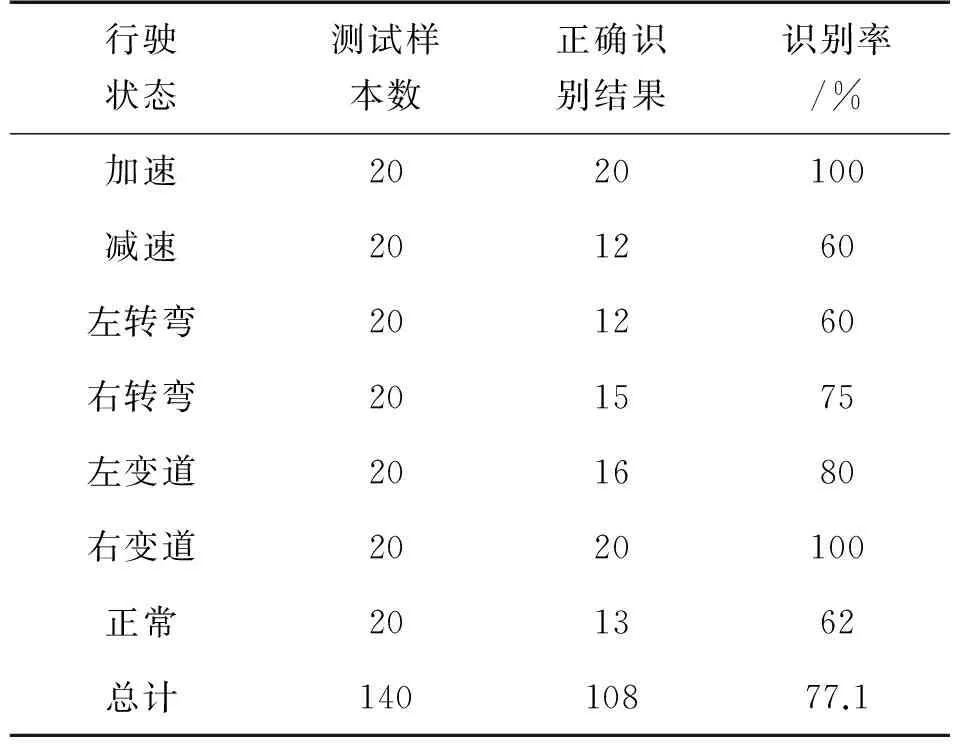
表2 基于ODB信息的识别结果(基于随机森林)

5.4 基于加速度信息和OBD信息融合的驾驶状态识别

从上面两个实验可以看出,加速度信息和OBD信息都可以对驾驶行为进行简单的分类,但是其识别精度远远没有达到我们所期望的高度,因此,在这里,将两种信息源进行融合,以达到补充信息的效果。通过特征融合的方法得到的分类结果如表3所示。

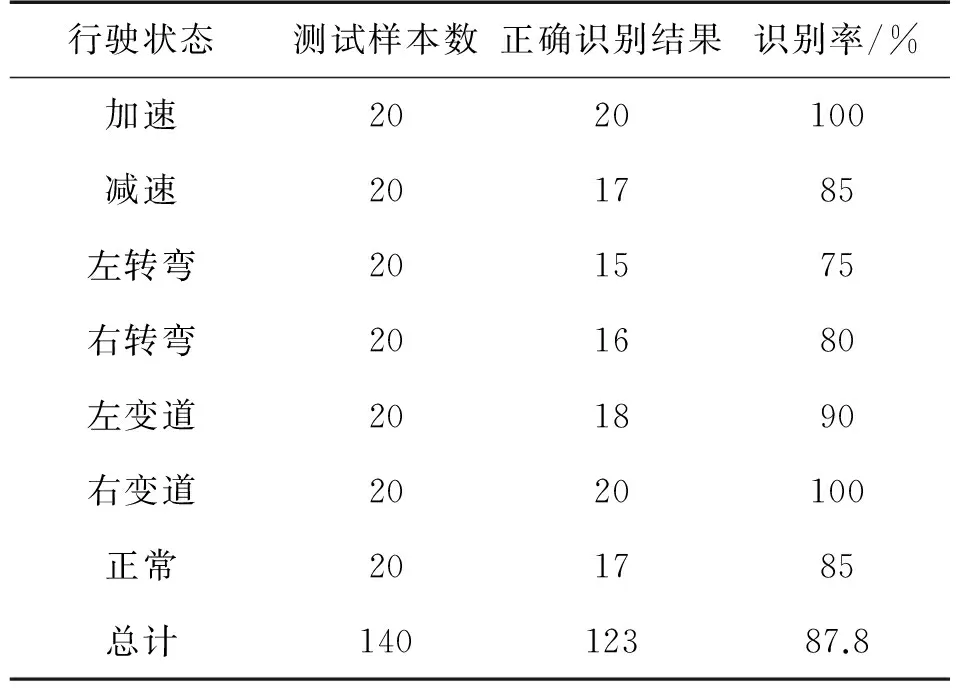
表3 基于信息融合方法的识别结果(基于随机森林)

5.5 实验结果分析

从5.2的实验结果可以看出,通过三轴加速度信息可以粗略的将电动汽车的驾驶行为辨识出来,但是其精度远远没有达到预期的目标,因为一些驾驶行为是一个综合的过程,转弯的过程同样也伴随着减速,而每次驾驶行为的操作也不尽相同,而这需要大量样本数。从5.3实验的实验结果可以看出,OBD信息中的速度、电机转速和输出电流对与不同驾驶行为也具有不错的辨识度。而通过5.4的实验结果可以看出,通过融合算法,将加速度信息和OBD信息融合可以有效的提高电动汽车的驾驶行为辨识度。

6 总结与展望

本文提出了一套基于信息融合的驾驶状态识别的方法,以期望能达到准确识别驾驶状态的目的。首次将MMA算法应用于加速度信号的特征提取,同时,通过信息融合的方法将加速度信息和OBD信息结合起来,达到提高分类精度的目的。但是还有一些方面需要提高:①本文中选取5 s作为一个固定时间窗口,这不一定是最为合适的,还需要大量的实验来选取最好的时间窗。②后续的工作中可以设计出一套完善的系统,在分类结束后返回客户端显示。

[1] 张文亮,武斌,李武峰,等. 我国纯电动汽车的发展方向及能源供给模式的探讨[J]. 电网技术,2009,33(4):1-5.

[2] 贺克斌,郝吉明,傅立新,等. 我国汽车排气污染现状与发展[J]. 环境科学,1996(4):80-83.

[3] Miyajima C,Nishiwaki Y,Ozawa K,et al. Driver Modeling Based on Driving Behavior and Its Evaluation in Driver Identification[J]. Proceedings of the IEEE,2007,95(2):427-437.

[4] 李伟健,林亚平,叶松涛. 智能手机碰撞检测及在汽车事故自救中的应用[J]. 计算机工程,2011,37(9):245-247.

[5] 周后飞,刘华平,石红星. 智能手机车辆异常驾驶行为检测方法[J]. 智能系统学报,2016,11(3):410-417.

[6] Kokosinska D,Gieraltowski J J. The Analysis of Human Heart Rate for Healthy and Ill Patients Using the Recently Published Method Multiscale Multifractal Analysis[C]//Computing in Cardiology Conference. IEEE,2014:425-428.

[7] Gieraltowski J,Hoyer D,Schneider U,et al. Assessment of Fetal Development Using Multiscale Multifractal Analysis of Heart Rate Variability[J]. ,2013:93-96.

[8] Wang J,Shang P,Cui X. Multiscalemultifractal Analysis of Traffic Signals to Uncover Richer Structures[J]. Physical Review E Statistical Nonlinear and Soft Matter Physics,2014,89(3):032916.

[10] ZHUANG Jinfa,LUO Jian. Fault Diagnosis Method Based on Modified Random Forests[J]. Computer Integrated Manufacturing Systems,2009(4):777-785.

[11] Cutler D R,Edwards TC Jr,Beard K H,et al. Random Forests for Classification in Ecology[J]. Ecology,2007,88(11):2783-92.

[12] 沈静华,裴东兴,张瑜. 基于多传感器数据融合的准静态校准数据处理方法[J]. 传感技术学报,2017,30(7):1040-1043.