火星多光谱相机的地面几何标定研究

关昭，乔卫东，杨建峰，薛彬，陶金有

（1. 中国科学院 西安光学精密机械研究所，西安 710119；2. 中国科学院大学，北京 101408）

引 言

为了解火星上的水形成及生命现象存在性，近50年来，世界各空间大国掀起了对火星探测的航天热潮。为满足火星探测活动的直接观测，描述火星表面的光谱特征，需选用一台集成光、机、电、热等多系统于一体的多光谱相机作为火星探测巡视器的有效载荷。为了对相机诸多功能的性能进行调试和测试，消除仪器误差，需要对相机的有关参数进行精准的定量测量，这一过程称为相机标定。相机标定主要分为彩色标定、辐射标定、光谱标定、几何标定及在轨标定几类，通过检测成像质量，完成色彩校正、目标物辐射能量校正、光谱校正及几何畸变校正等成像探测任务，实现地貌探测，掌握火星表面物质类型分布的主要科学任务。

其中基于成像的几何约束关系，求解相机内部参数（焦距，主点，畸变系数），得到相机与地物位置关系的标定内容称为几何标定。针对相机内部参数固定的情况，在无星上相关单元的条件下，对相机的内部参数进行探测和检验时，地面几何标定是非常有必要的。在已测畸变的情况下，本文主要探究相机焦距、主点的获取及其精度问题。根据实际工程应用需求，提出重投影误差小于0.3pix，焦距误差小于1%的指标要求。火星多光谱相机共有8个光谱通道（480、525、650、700、800、900、950及1 000 nm），6个调焦位置（1.5、3.1、4.0、5.6、9.4及28.1 m），需要对每个光谱通道的调焦位置均进行几何标定，实现参数归一化，矫正图像畸变，完成图像融合，镶嵌，并最终使用该固定内参实现火星地貌三维重建的科学任务。

首先，普通测绘相机的几何标定都是针对无穷远目标，但针对本次近距离目标成像，且距离变化范围较大（1.5～28.1 m）的特殊情况，标定方法应有所调整；其次，火星相机是一台具有8通道的多光谱相机，对于任一物距的不同光谱通道，其测量参数均有不同，故需逐个进行标定。基于以上两点，为高效率获得某一光谱条件下有限远成像时相机的内部参数，采用算法标定法。目前算法标定主要有3种方法：传统相机标定法、主动视觉相机标定法和相机自标定法。根据王卫文的总结：基于主动视觉相机标定法需利用摄像机某些运动信息来线性求解模型参数，但对于相机运动信息未知和无法控制的场合则不能运用，加之实验设备昂贵，实验要求较高，故该方法实用性不强[1]；自标定法仅依靠多幅图像之间的对应关系来完成参数计算，灵活性较高，由于其多解性和噪声造成的低鲁棒性导致解的精度不高[2]；传统的相机标定法虽需使用精度较高的标定板，但适用于任意摄像机模型，且标定精度较高[13-16]。由于火星多光谱相机的调焦档位固定，拟用传统相机标定法完成多光谱相机的标定工作。

传统相机标定法主要包括直接线性变换法、Tsai两步法、张正友算法及Heikkilä算法等。通过大量研究前人成功的经验，认为每种标定技术均有优点，但也含缺点，我们企图把各种标定技术的优点予以重新组合，找出自己的标定思路。邱茂林提出：直接线性变换法虽可通过求解线性方程的手段就可获得相机模型参数，但却忽略了成像过程中的非线性畸变问题[3]；Tsai两步法在直接线性变换法的基础上[4-6]，考虑畸变因素，并利用最优化算法进一步提高定标精度，但由于仅仅考虑径向畸变而导致成像模型不够准确；张正友算法在对标定板要求并不高[7]的情况下仍具有良好的鲁棒性，但柳溜指出：成像距离对张正友算法的精度影响较大[8]；Heikkilä算法精确度较高，且不受物距影响算法精度，但需提供具有良好鲁棒性的初始值，综上所述本文在选择张正友算法基础上改进的Heikkilä算法。

1 标定原理

传统标定法中，首先通过小孔成像模型建立高精度靶标上的特征点与其影像点间的投影关系，再添加畸变约束，最终通过非线性优化得到相机内部参数。

Heikkilä算法精度较高，但需提供具有抗噪性的初始值。使用鲁棒性强的标定初值是完成非线性优化，得到准确参数中至关重要的第一步。张正友算法中验证了该方法下所得噪声中估算参数保持非常稳定（其误差小于0.02%[7]），可获得具有抗噪性的稳定相机参数，因此本文在清晰成像的基础上，先使用具有抗噪性的张正友算法得到鲁棒性较好的内外方位元素初始值，通过迭代搜索获得优化结果，并代入后向相机模型中求出畸变系数，同时得到经过非线性优化的待求参数，最终通过估算参数的不确定度，评判算法的有效性。

1.1 张正友算法

标定模型通常使用线性针孔模型，将世界坐标系的特征点投影到像素平面中[9]，令三维空间中任意一物点Q（X，Y，Z）对应像素坐标系中的像点坐标为q（u，v），用=（u，v，1）T和=（X，Y，Z，1）T分别表示像方，物方的齐次坐标。

由针孔模型的共线条件可知

图1 针孔模型Fig.1 Pinhole model

根据旋转矩阵中向量的标准正交性，用最小二乘法建立关于P-TP-1的方程，后通过cholesky分解求取内方位元素矩阵P，进而求取外方位元素矩阵[R t]。

由于上述求解过程只是得到了最小代数距离，不具有物理意义，因此还需要最大似然估计对其进行优化，给定t幅图像，每幅图有s个控制点，假设像点被独立同分布的噪声污染，则最大似然估计可由下式表示

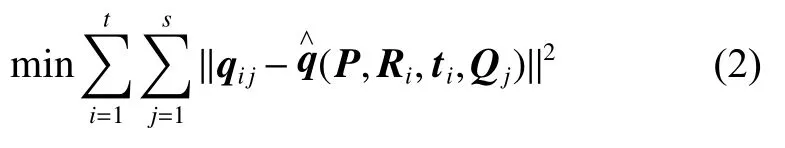
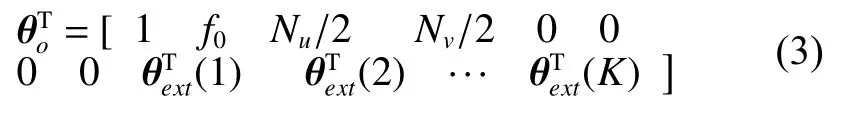
为迭代搜索提供初值，其中：Nu,Nv为水平和竖直方向的尺寸；f0为焦距；为第K幅图的外方位元素。

1.2 迭代搜索

上节得到线性模型下的求解参数后，通过最大似然估计完成优化。本章考虑噪声干扰，在前向相机模型中进一步对所得参数实现非线性优化。迭代搜索基于马氏距离的判别，通过最小化观测值与模型之间平方差的加权和实现计算值逼近观测值。假设有t幅图像，且每幅图形有s个控制点，用eo(s,t)表示第t幅图中观测图像坐标系下角点s，ed(s,t)为前向相机模型中相应的解算向量，故目标函数表示如下[10]

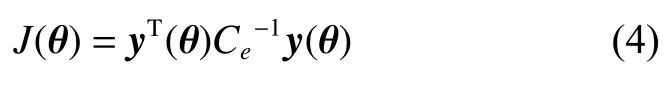
其中

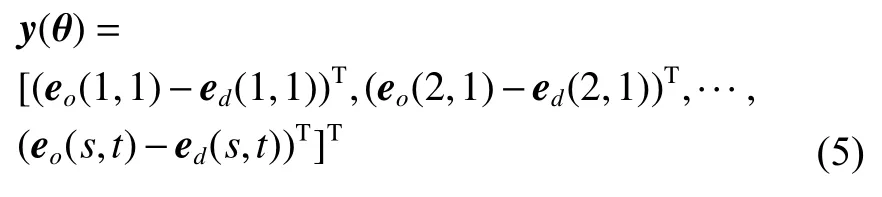
测量噪声的协方差矩阵

其中：Ce(s,t)=E{[eo(s,t)-E{ed(s,t)}][eo(s,t)-E{ed(s,t)}]T}，该值可从相同位置和方向拍摄的不同照片中得到。最终前向相机模型中的参数通过下式得到

1.3 后向相机模型

在许多应用中，都需要将观测图像坐标再投影到三维坐标空间中，在这一步骤中，通过前后向模型的一致性，得到畸变系数δ=[k1,k2,...,p1,p2,...]T，其中k1,k2,...,为径向畸变系数，p1,p2,...为切向畸变系数[11]，畸变系数因切向畸变较小，为增加解算稳定性，故将其设置为0，畸变系数通过下式计算得出

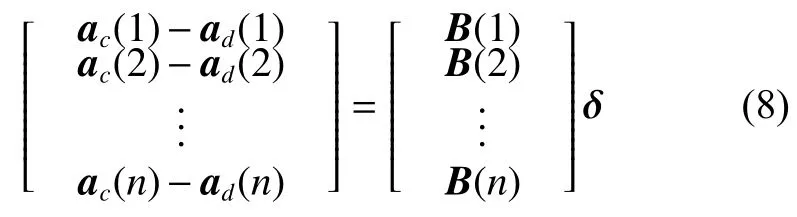
其中：

理想坐标ac=[u,v]T，

实际坐标ad=[ud,vd]T

1.4 不确定度分析

不确定度分析表征计算结果的分散性和计算值的可信赖程度。不确定度越小，表示计算结果越接近真实结果，越可靠，反之亦然。利用检测误差及所建模型求得最终结果的偏差程度，并以此为标准，衡量本文算法的精确程度。

参考文献[12]，假设共有t幅图，每幅图有s个控制点，因每次使用同样步骤提取角点，根据其观测独立性可假设图像对应角点坐标q（u，v）是协方差阵为σ2I的随机量，根据共线模型（1）可得

P=[PAPB]是待求参数，

因为空间点一般为高精度的确定量，故式（11）式可简化为

根据误差扩散理论（见文献[12]），标定参数P的协方差矩阵为

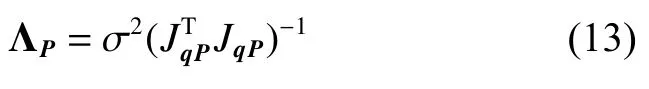
(i=1～t)

则

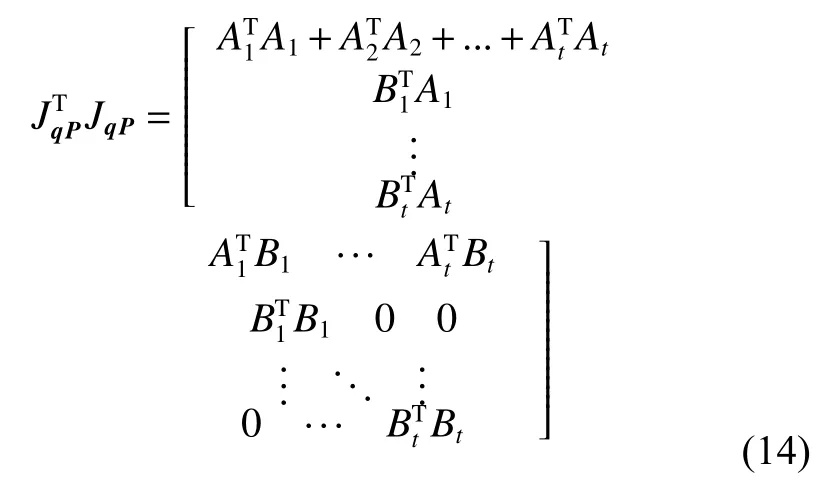
当空间模板特征点数目增加时，

即ΛP每个参数方差减少。

2 标定过程

选取棋盘格角点作为世界坐标系下的观测点，用火星多光谱相机固定光谱通道及调焦档位对不同位姿，覆盖一定物距范围内的标定板进行拍摄，并获取观测点影像在图像坐标系的坐标，通过标定模型，解算出相机内参，最后用求解的内部参数和观测点世界坐标来估计观测点影像，并与实际影像点比较，将两者之间的误差作为评判算法精度的重要依据。

2.1 实验条件及注意事项

本次标定任务需要的实验器材包括多光谱相机，升降台，以及固定支架等仪器。根据Heikkilä所述，为减少光照差异而导致的标定偏差，故选择室外条件下进行照片采集[14]。本次实验数据的处理在matlab 2017a的软件平台下完成。

数据采集的过程中需使定标版出现的所有位置占据整个视野范围，且单幅图像中标定板占比达到70%左右。为降低相机内参间的相干性，应对标定板进行多角度，多物距的拍摄。张正友提出当标定板与像平面夹角约为45°时，得到误差较低的标定结果[7]，故采集数据过程中使位姿变换的定标版与相平面的夹角成45°左右。此外，陈晓燕通过实验得到张氏算法中使用图片的数量在20～30为宜[15]，且因视野边缘畸变较大，故边角处需要拍摄多幅照片，所以本次实验选择定标版在视野范围的4个边角及中心处，不同物距，不同姿态的图片中各选5幅图，最终使用25幅。

2.2 采集数据

如前所述原理，需要在像平面内检测棋盘格角点作为像点坐标来列写公式（2），其图像的质量将直接影响检测精度。拍摄过程中，噪声污染并不明显，未能形成视觉障碍，但像质模糊却成为降低图像质量的主要因素。因此本文主要探讨怎样采集画面清晰的图像。

分析表明，正确对焦的情况下，图像边缘清晰可辨，包含信息最丰富，但随着离焦量的增加，图像变得模糊，边缘平滑，其信息含量减少。故可通过提取图像的边缘信息反映图像的清晰度，并生成判别函数。在确定好相机与标定板的位置关系后，再由判别函数找到合适的调焦位置。参考文献[16]中方法，将该过程分为以下5步。

第1步：找出像素点的最大灰度差方向，I为原图，h为点扩散函数。

最大灰度梯度方向图像为

第2步：引入阈值，去除图像平坦区域的梯度影响因素，利用Ostu分割算法得出理论最佳阈值T，得到新的灰度梯度图像G′

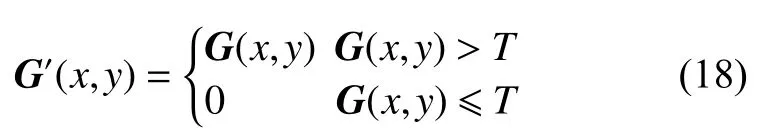
第3步：通过对灰度梯度图像G′所在边缘8邻域内搜索来剔除孤立噪声产生的伪边缘

其中：Edge(x,y)为像素点（x，y）的8邻域中的边缘点个数。

第4步：生成归一化的清晰度评价函数

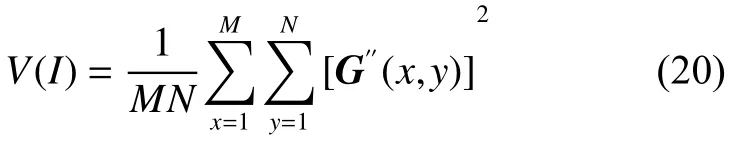
根据该评价函数的单峰性和无偏性，找出极值所对应的像面位置，此时成像最清晰，得到图2，符合人眼评判标准。

图2 像面为清晰评价函数峰值处的成像Fig.2 The image which is at the peak of the function for sharp evaluation

第5步 使用本文算法，得到准确的标定结果。

3 实验结果与分析

为满足工程需要，需对8个光谱通道，6个调焦位置，共48组相机内部参数进行标定，并提出重投影误差小于0.3 pix，焦距误差小于1%的指标要求。

因本文在现有算法基础上，不但完成了三维空间中特征点投影到像平面的前向模型计算，还引入了像点到三维特征点的后向模型优化，故待求参数的精度较高，不确定度较小，其焦距不确定度达到0.7‰，视场内主点不确定度可达3.1%；因使用鲁棒性较高的张正友算法初值，故后续非线性优化算法的参数准确度更高，计算速率也有所提高。表1是本文算法与张正友EasyCalib软件计算结果的对比（第8通道，调焦位置1的数据）。

表1 本文算法和张正友算法对比Table 1 The contrast between our method and Zhang's

从表中可知，即使在过曝情况下，本文计算结果与张氏算法相差不大，且误差平方和仍较张氏算法有小幅下降；当剔除因过曝导致误差偏大的角点后，本文算法的误差平方和显著下降，证明本文算法的有效性。

为证明达到指标要求，本文另外计算重投影误差及各参数的不确定度，如表2所示，在过曝情况下，角点提取不准确导致参数的不确定度较大[17-19]，且重投影误差超过应用指标0.3 pix；当在正常情况下，本文所得内参不确定度均有所下降，重投影误差为0.25 pix，满足实际应用。

表2 参数精度指标Table 2 The accuracy of parameters

为探究焦距误差，现以第5、6个光谱（800，900 nm）通道为例进行说明，分别计算在第5、6光谱通道中6个调焦位置的焦距，如表3～4所示，焦距误差如图3。

图3 本文所得5、6通道焦距值与光学仿真焦距值的误差曲线Fig.3 The deviation curve of focal length value on the fifth，sixth channel obtained by comparing our algorithm and optical simulation

表3 第5通道6个调焦位置的焦距Table 3 The focal length of 6 focusing positions on the 5th channel

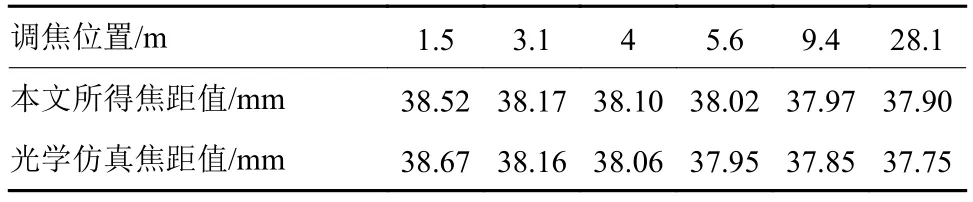
表4 第6通道6个调焦位置的焦距Table 4 The focal length of 6 focusing positions on the 6th channel

由于本文针对的应用都是小物距（成像光线并非平行光）情况[20-21]，故严格意义下所求相机参数应为像距，但根据视觉领域通用说法，将其称为焦距。由焦距误差曲线可知，其值都控制在5‰，远小于1%，满足应用要求。由图3分析得知，物距较小时，光学仿真值大于算法值，而随物距的增大，光学仿真值和算法值都有所下降，且算法值下降速率越来越缓，直至最后大于仿真值[22]。这是因为在光学模型中，由高斯公式可知焦距与物距存在倒数关系，而算法模型中，由张正友算法模型知焦距与物距的关系大约是倒数的开根。故当物距增加时，误差出现从负到正的过程，且变化规律基本满足倒数及其开根的混合运算。

4 结 论

本算法在获得清晰图像的基础上，使用张正友算法与Heikkilä算法结合的方法完成几何标定后，分别对比本文结果，张正友算法，及光学仿真值，验证重投影误差及焦距误差满足实际应用需求。实验表明，即使在过曝情况下，本文算法精度仍稍高于张正友算法，鲁棒性更强，未来的工作将通过数据拟合的方法进一步探究物距和焦距之间的关系，优化相关参数，使得模型更完善，标定结果更准确；同时需探究处理图像畸变的相关内容，实现图像几何畸变校正，提高其位置精度。