三维应力下破碎砂岩渗透特性试验研究

张天军，石　涛，潘红宇，陈　阁

(1.西安科技大学 理学院，陕西 西安 710054；2.西安科技大学 安全科学与工程学院，陕西 西安 710054)

0　引　言

在采矿工程中，受采动影响破碎岩体常常再次承压，其孔隙、裂隙发生显著变化，与完整、致密岩体相比其孔隙疏松、渗透性强，而大多数事故灾害由于破碎岩石中的非稳态渗流引起的[1]。因此，对于承压破碎岩体中的渗流研究显得十分必要。目前针对侧限条件下破碎岩石以及确定围压下标准样渗流的研究成果较多，一方面，从破碎岩石压实过程考虑，刘卫群对破碎岩石进行了渗流试验研究，得到了其渗透系数变化规律[2]；黄先伍通过拟合20～25 mm粒径破碎砂岩中渗流时的渗流速度与孔压梯度，得到了不同孔隙率下破碎砂岩的渗透率和非Darcy流β因子，并建立了孔隙率随渗透特性参数的变化关系曲线[3]；另一方面，针对粒径大小对其渗透特性的影响，李顺才等人对破碎岩样进行了渗透试验研究，得到了不同粒径破碎岩样的渗透特性参数随孔隙度的变化规律[4-6]；Mohammad S研究了6种不同尺寸的堆石体的渗流行为，并采用不同的孔隙压力来评估其渗流特性[7]；Cherubini C基于Forchheimer方程分析了破碎煤岩体的渗流规律[8]；而对于标准岩样而言，孙培德考虑围压和孔隙压力对完整煤样渗流的影响，并对其进行了试验研究，得到了含瓦斯完整煤变形过程中的渗透率变化规律[9]；王伟、彭苏萍研究了完整岩石在不同围压和渗透压下的渗透特性，分析了全应力-应变变化过程中渗透率随围压、渗透压和体积应变的变化规律[10-11]，张改玲对砂土进行了高围压条件下的渗透试验，得到了粗细砂土在不同围压下渗透特性的变化规律[12]。但对于围压影响下破碎岩石渗透特性的试验研究尚未深入。文中针对不同级配下破碎砂岩中的渗流稳定性问题进行了研究，得到了其渗透参数随孔隙度的变化规律，并结合破碎岩体失稳动力学理论对其稳定性进行了分析[13]。在上述已有研究的基础上，文中探索围压对破碎岩石渗流时的影响，利用自主研发的破碎岩石三轴渗透试验系统，基于稳态渗透法和位移控制法，对不同围压下破碎砂岩进行渗透试验，得到破碎岩石的渗透特性变化规律。

1　试验系统及方法

1.1　试验系统及岩样的制备

试验利用本实验室研发的破碎岩石三轴渗流试验系统，该系统包括电子万能试验机DDL 600，渗透装置、渗透液液压系统、围压液压系统、电子分析天平和计算机等，如图1所示。

图1　试验装置图Fig.1　Test apparatus

本试验所用的砂岩岩样取自陕西澄合矿务局董家河煤矿，该矿煤层顶底板多为砂岩，且存在富集水异常区，受采动影响可能发生突水事故。通过将其制成标准样来获取砂岩的岩芯密度，密度为ρ=2 548 kg/m3.利用破碎机将试验所用的岩石进行破碎，然后通过分选筛选出粒径为5～10 mm的岩样，并称取400 g破碎岩样以备实验所用。

1.2　试验方法

对于破碎岩石渗透特性研究应采用稳态渗透法[14]。因此，试验采用稳态渗透法与轴向位移控法来进行破碎岩石的渗透特性研究。松散破碎岩石具有较强的流动特性，且孔隙较大、渗透性强。而围压及轴向压缩位移的改变均会使破碎岩石的宏观体积发生改变，进而导致散体孔隙度的变化。其中，孔隙度是衡量散体渗透参数的一个重要指标，因此，散体孔隙度的研究对渗流具有重要的意义。该试验系统的内缸桶被设计为可变形的，内缸桶是由多个圆环构件从下到上依次叠放在一起，并将4个销钉分别穿入上下对齐的四组上销钉孔、中间销钉孔和下销钉孔中，并用电工胶带从下到上将下压头与内缸筒缠绕在一起，除4个销钉即成，如图2所示。通过可调节围压和轴向压缩位移，可以更加真实描述承压破碎岩石在不同孔隙下的渗透特性，对于可控围压下破碎岩石中的渗流稳定性研究具有重要的意义。因此，采用位移控制法来研究破碎岩石在不同孔隙下的渗透特性变化规律。

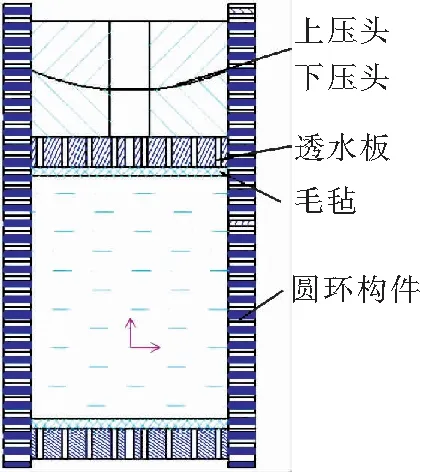
图2　内缸桶圆环结构剖面图Fig.2　Inner cylinder barrel ring structure profile

通过对其标准样的力学特性测试，测定出其抗压强度为45.43 MPa，根据其强度确定出其渗透压及围压值的大小，围压值、渗透压值根据岩体在矿区测量位置时采集的数据进行设定。试验采用位移控制法，共设定4级轴向位移(4，8，12，16 mm)，在每一轴向位移下设定5级围压(3，3.5，4，4.5，5 MPa)，再在不同围压下设定4级渗透压(0.5，1，1.5，2 MPa)。试验采用的渗透液的密度ρ为：874 kg/m3，动力粘度μ为：1.96×10-2Pa·s.试验步骤如下。

试验开始时岩样下压到设定位置，先通渗透液使试样达到饱和状态，再停止渗透液压系统工作并立即关闭回流阀门，直到管路出口处不再流出渗透液为止，再加围压到设定值并量取从破碎岩样挤压出来的渗透液质量，直到管路出口不再流出为止。此时，再打开阀门并开启液压泵对破碎岩样按照4级依次递增的渗透压渗流，完成后并记录试验数据，再加到下一级设定围压时，重复上述试验过程直到5级围压下的渗透试验结束，并记录试验数据。然后卸围压，紧接着下一级位移下，重复上述试验过程，直到完成4级位移下，每一级位移下的不同围压下的渗流试验，记录相关试验数据，试验结束。

试验时，将400 g破碎岩样放置渗透装置的内缸筒然后进行密封，再将其放置实验台后使加载压头与活塞紧密接触，并测量压头露出高度进行记录。按照上述试验步骤，来测量每一级位移下，5级围压下的各级渗透压下的渗流量Q，通过渗流Q可计算出每一级位移下，不同围压下的各级渗透压下的渗流速度v。破碎岩样的渗流速度可通过渗流量Q得到

(1)

式中Q为破碎岩体的渗流量，m3/s；Ais为渗流时破碎砂岩的实际横截面积，m2.

当进行渗流试验时，设p1为渗透仪上端渗透压力，设p2渗流出口气压，由于渗流出口与大气相连，故相对于大气压p2=0。因此，孔压梯度的计算公式如下

(2)

式中GP为孔压梯度，Pa/m；Hs为当前的试样高度，m；h0为破碎岩样的初始高度，m；Δh为轴向压缩位移，m.

内缸筒破碎岩样的初始高度计算

h0=h1+h2+h3+h4-h5-h6-h7-h8

(3)

式中h0为破碎岩体的初始高度，mm；h1为设置在底座顶部中间位置处的凹槽的深度，mm；h2为外缸筒高度,mm；h3为上桶盖厚度,mm；h4为活塞的露头高度，mm；h5为活塞总高度,mm；h6为充分接触在一起后上半凹面压头与上半凹面压头的总高度,mm；h7为下压头高度,mm；h8为透水板和毛毡的总厚度,mm，其中三轴破碎内缸桶的剖面图，如图3所示。

图3　破碎岩石三轴渗透仪剖面图Fig.3　Broken rock three axis penetration meter profile

孔隙度是描述破碎岩石变形及渗透特性最基本的要素[10]，因此对于承压破碎岩石中的渗流稳定性具有重要意义。

已有文献很少考虑围压对破碎岩石孔隙度的影响，是由于前人设计的试验装置对破碎岩石加载围压不易控制，但围压却是破碎岩石渗流过程中的一个重要影响因素。现结合上述研发的试验系统给出可控围压下破碎岩体的孔隙度计算方法，定义三维应力下破碎岩石的孔隙度：破碎岩石的孔隙度φ是由压头轴向压缩位移Δh以及前s级围压下挤出饱和试样中渗透液质量累积和Mis，以及破碎岩石颗粒之间的孔隙共同决定的，因此破碎岩石的孔隙度公式计算如下

(4)

式中m1为破碎岩样的质量，kg；Mis为i级轴向压缩位移下，内缸桶充满渗透液的破碎岩样在前s级围压下挤出内缸桶外的渗透液质量累积和，kg；Ais为i级轴向压缩位移下，s级围压加载后岩样的横截面积，m2；ρ为渗透液密度，kg/m3；ρ1为破碎砂岩的密度，kg/m3；Δh为试验初始设定的数值，mm.相比侧限条件下的孔隙计算公式，其能够较为真实的反映破碎岩石的孔隙特征，对于工程实际中承压破碎岩体中渗流研究具有一定的参考价值。

当轴向压缩位移下为Δh时，通过对试样进行围压的加载，假设从破碎岩样挤出的渗透液质量是由与砂岩岩样等高的渗流管路中挤出的，因此破碎砂岩的横截面积减小量为

(5)

因此，破碎砂岩的横截面积公式

Ais=A-As

(6)

式中A为内缸桶的横截面积，m2；As为横截面积减少量，m2；Ais为加载围压后破碎岩石的实际面积，m2.

2　试验数据与结果分析

2.1　渗透参数确定

试验以5～10 mm粒径的破碎砂岩为研究对象，对其进行不同轴向压缩位移下、不同围压下的渗流试验，得出其稳定时渗流速度v以及孔压梯度GP.通过对试验数据的处理发现，破碎砂岩的渗流速度v和孔压梯度GP之间不呈线性关系，说明破碎砂岩的渗流不服从Darcy定律。因此，采用Forchheimer经验公式拟合[15]，可得到渗透率k和非Darcy流β因子，见表1.其中Forchheimer公式为

(7)

2.2　试验现象与结果分析

由表1可建立破碎砂岩在轴向压缩位移4，8，12，16 mm的围压-孔隙度变化曲线关系，如图4所示。

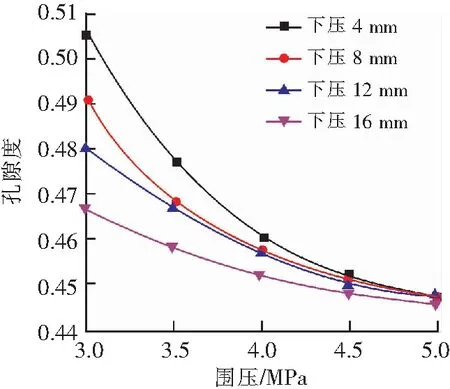
图4　围压-孔隙度曲线Fig.4　Curves of confining pressure-porosity

从图4可以看出，不同轴向压缩位移下，破碎砂岩的孔隙度随围压的增大呈减小趋势，且趋于一个稳定值。当围压小于4 MPa时，随围压增长，孔隙度减小幅度较大，属于快速压密阶段。在不同下压位移下试样的压缩变形量不同，主要原因为破碎砂岩颗粒处于松散状态，骨架结构抗变形能力小，在外力作用下破碎砂岩的孔隙快速闭合，孔隙充填速度较快；当围压大于4 MPa时，试样的孔隙度减小速率逐渐减缓，属于缓慢压密阶段，主要是砂岩颗粒经历了前期的压缩，导致大量颗粒再次破碎、细化，这些细小颗粒充填了大量的孔隙，颗粒间的接触面积增大，摩擦力增大，环向变形量进一步减缓。破碎砂岩逐渐形成了具有一定支撑能力的结构，抗变形能力增强，孔隙结构趋于稳定。

表1　5～10 mm破碎砂岩的渗透特性参数

将图4的不同轴向压缩位移下的围压-孔隙度曲线进行拟合，通过拟合的结果发现不同轴向压缩位移下，破碎砂岩的围压-孔隙度之间都近似呈对数关系，两者之间拟合的相关系数R2均在0.94以上，其围压-孔隙度关系式

φ=aln(σ)+b

(8)

式中a，b均为拟合系数；σ为围压，MPa.

由表1建立同一围压下孔隙度随不同轴向压缩位移的变化曲线关系，如图5所示。

图5　轴向压缩位移-孔隙度曲线Fig.5　Curves of press displacement-porosity

从图5可知，随轴向压缩位移的增大，破碎砂岩的孔隙度总体呈减小趋势，围压越大，孔隙度的减小趋势越加平缓。当围压为3 MPa时，随轴向压缩位移增加，破碎砂岩的孔隙度减小幅度明显，孔隙度的降低率最大为7.6%，主要是颗粒的聚拢效果较差孔隙较大，轴向压缩时颗粒的脆性破坏明显，轴向变形量大。当围压为5 MPa时，孔隙度变化趋势平缓，孔隙度的降低率为0.35%，主要原因是颗粒进过前几级的载荷作用，颗粒破碎量加大，使散体的可压缩体积减小，颗粒排列紧密、滑移充填减弱，抗变形能力增强。

表1可建立破碎砂岩的围压与渗透率、轴向压缩位移与渗透率以及围压与非Daray流β因子关系曲线，如图6，7，9所示。

图6　围压-渗透率曲线Fig.6　Curves of confining pressure-permeability

从图6可以看出，破碎砂岩的渗透率量级在10-11～10-13m2之间，渗透率降低率达到87.4%.随着围压的增大，试样的渗透率整体呈现减小趋势，围压越大，渗透率减小量越小，主要原因是破碎砂岩的可压缩体积不可能无限减小。当围压小于4 MPa时，破碎砂岩的渗透率随围压的增大明显减小，表现为砂岩骨架疏松，颗粒间的孔隙较大，在外力作用下颗粒便于向环向流动，流动过程中部分颗粒被挤压甚至压碎，颗粒间相互接触面积越来越大，渗流孔隙通道半径快速减小，细小颗粒随渗透液的流动不断的迁移，导致部分渗流通道很大程度的堵塞。当围压大于4 MPa时，随围压的增大，渗透率逐渐缓慢降低，表现为颗粒再次破碎的程度增加，细小颗粒在破碎砂岩中占得比例逐渐上升，砂岩的密实度较大且缓慢增加，致使孔隙减小或闭合，渗透率的值逐渐趋于稳定。

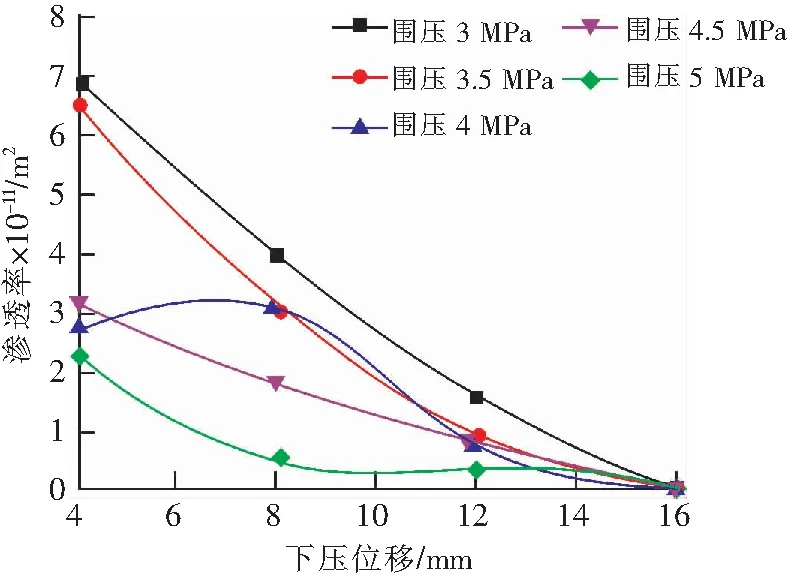
图7　轴向压缩位移-渗透率曲线Fig.7　Curves of press displacement-permeability

从图7可以看出，随着轴向压缩位移增大，破碎砂岩的渗透率呈非线性减小，且差异性逐渐缩小。当轴向压缩位移小于10 mm时，破碎砂岩渗透率的减小幅度较大，主要原因为颗粒间的孔隙较大，且孔隙连通性强，渗透液与孔壁的粘滞阻力较小，渗流时渗流量较大。随着轴向压缩位移的增加，颗粒的破碎程度逐渐增大，导致颗粒的原有级配发生显著改变，造成孔隙的不确定性等，其中再次分解、细化的颗粒在较大轴向压缩位移下及围压下逐渐发生聚拢、压密，破碎砂岩的渗透率最终趋于一个稳定值。

在轴向压缩位移及围压的增大过程中，破碎砂岩渗透率的减小过程中出现了局部波动，现分析如下

当破碎岩石承受较大的应力时，其孔隙越小，孔隙中渗流量也较小，为了研究渗透液在复杂孔隙通道的受力情况及其理论推导，故假设孔隙通道为毛细管路是十分必要的。因此，当渗流稳定时，假设渗流管路为等径毛细管，流动液为牛顿流体，取一段微元体，作用在微元体流向上的压力为FP，摩擦阻力为FS，FP，FS分别为[16]，其中毛细管示意图，如图8所示。

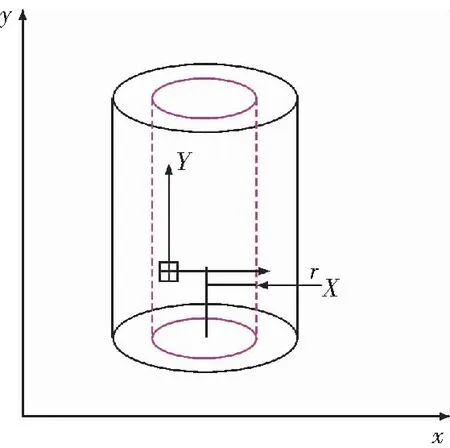
图8　毛细管示意图Fig.8　Schematic diagram of capillary

FP=πr2(p1-p2)

(9)

FS=2πτrl

(10)

式中l为毛细管的长度，m；τ为切应力，MPa.

则根据破碎砂岩中的渗流速度稳定时得出

FP=FS

(11)

由此可得切应力表达式，再联立牛顿内摩擦定律得

(12)

联立(9)、(10)、(11)、(12)得

(13)

对式(13)积分可得

(14)

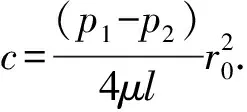
(15)

式中Aj为某一毛细管路的横截面积，m2.

则破碎砂岩横截面积的渗流总流量可以表示为[17]

(16)

式中n为试样横截面积上的毛细管路总数目。

围压影响下破碎岩石的孔隙度可以表示为

(17)

从上述公式可以看出，破碎砂岩在不同轴向压缩位移下，随围压的增大，毛细管的横截面积Aj和孔隙数目的减小，导致渗流质量Mis增加速率减缓，即孔隙度减小量趋于定值，导致渗透率减小，主要是试样的渗流孔隙通道减小，并且毛细管壁上的细小颗粒具有不稳定性，随时可能被渗透液冲刷再次运动到达一个相对稳定的位置。细小颗粒随渗透液迁移造成孔隙的堵塞，或是孔隙、裂隙的闭合或延伸等，导致毛细管孔径大小不断地变化使渗透率出现局部波动。

图9　围压-非Darcy流β因子曲线Fig.9　Curves of confining pressure-non-Darcy flow factor

从图9可以看出，随围压的增大，破碎砂岩的非Darcy流β因子值均呈增长趋势，其中非Darcy流β因子的值量级在108～1011m-1之间。当围压小于4 MPa时，破碎砂岩的非Darcy流β因子变化趋势平缓，非Darcy流现象不明显，这是因为破碎砂岩颗粒再次破碎、细化量较少，大颗粒的棱角作为试样的应力骨架，致使孔隙贯通率仍然较大，渗流时渗流量较大。当围压大于4 MPa时，非Darcy流β因子值增长趋势明显，是因为随围压的增大，砂岩颗粒的破碎、细化量占有比例大，颗粒的骨架排列紧密，试样的密实度增大导致破碎砂岩有效孔毛细管孔径及数目均减小，渗流时渗透液与孔壁之间的相对接触面积增大。特别是破碎砂岩毛细管孔径越小，其非Darcy流渗透特性越加明显[18]。

3　结　论

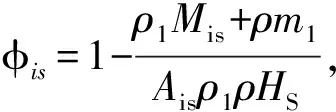
2)不同轴向压缩位移下，渗透液在破碎砂岩中的渗流呈非Darcy流特性，其渗透率、孔隙度随围压升高而减小，且差异性逐渐减小，最终趋于一个稳定值，表明有效孔隙的连通性减弱，整体结构趋于稳定；

3)破碎砂岩的渗透率量级从10-11m2降低到10-13m2，而非Darcy流β因子的量级从108m-1增加到1011m-1，试样的渗透率和非Darcy流β因子的变化趋势受围压或轴向压缩位移影响，使毛细管孔径减小，导致渗透液与毛细管孔壁的相对接触面积增加；

4)破碎砂岩颗粒的破碎、细化程度以及试样的密实度对渗透率和非Darcy流β因子影响很大，主要原因是渗流孔隙通道的闭合或产生、延伸以及贯通等，使孔隙通道变化具有不确定性和复杂性。

参考文献(References)：

[1]李树刚，徐精彩.软煤样渗透特性的电液伺服试验研究[J].岩土工程学报，2001，23(1)：68-70.

LI Shu-gang，XU Jing-cai.Experimental study on permeability of soft coal sample with electro-hydraulic servocontrolled testing syetem[J].Chinese Journal of Geotechnical Engineering，2001，23(1)：68-70.

[2]刘卫群，繆协兴，陈占清.破碎岩石渗透性的测定方法[J].实验力学，2003，18(1)：56-61.

LIU Wei-qun，MIAO Xie-xing，CHEN Zhan-qing.Determination of the permeability of the rock crusher[J].Journal of Experimental Mechanics，2003，18(1)：56-61.

[3]黄先伍，唐平，缪协兴，等.破碎砂岩渗透特性与孔隙率关系的试验研究[J].岩土力学，2005，26(9)：1385-1388.

HUANG Xian-wu，TANG Ping，MIAO Xie-xing，et al.Testing study on seepage properties of broken sandstone[J].Rock and Soil Mechanics，2005，26(9)：1385-1388.

[4]李顺才，缪协兴，陈占清，等.承压破碎岩石非Darcy渗流的渗透特性试验研究[J].工程力学，2008，25(4)：85-92.

LI Shun-cai，MIAO Xie-xing，CHEN Zhan-qing，et al.Experimental study on seepage properties of non-darcy flow in confined broken rocks[J].Engineering Mechanics，2008，25(4)：85-92.

[5]李顺才.不同孔隙率下破碎灰岩渗透特性试验研究[J].徐州工程学院院报，2009，24(1)：17-24.

LI Shun-cai.Experimental study on the seepage properties of broken limestone at different porosity rate[J].Journal of Xuzhou Institute of Technology，2009，24(1)：17-24.

[6]李顺才，陈占清，缪协兴，等.破碎岩体流固耦合渗流的分岔[J].煤炭学报，2008，33(7)：754-759.

LI Shun-cai，CHEN Zhan-qing，MIAO Xie-xing，et al.Bifurcation of fluid-solid couping flow in broken rock[J].Journal of China Coal Society，2008，33(7)：754-759.

[7]Mohammad S，Salehi R.Non-darcy flow of water through a packed column test[J].Transport in Porous Media，2014，101(2)：215-227.

[8]Cherubini C，Giasi C I，Pastore N.Bench scale laboratory tests to analyze non-linear flow in fractured media[J].Hydrology and Earth System Sciences，2012，16(8)：2511-2522.

[9]孙培德.变形过程中煤样渗透率变化规律的实验研究[J].岩石力学与工程学报，2001，20(增刊)：1801-1804.

SUN Pei-de.Testing study on coal specimen permeability during solid deformation process[J].Chinese Journal of Rock Mechanics and Engineering，2001，20(Suppl.)：1801-1804.

[10]王伟，徐伟亚，王如宾，等.低渗透率岩石三轴压缩过程中的渗透性研究[J].岩石力学与工程学报，2015，34(1)：40-47.

WANG Wei，XU Wei-ya，WANG Ru-bin，et al.Permeability of dense rock under triaxial compression[J].Chinese Journal of Rock Mechanics and Engineering，2015，34(1)：40-47.

[11]彭苏萍，孟召平，王虎，等.不同围压下砂岩孔渗规律试验研究[J].岩石力学与工程学报，2003，22(5)：742-746.

PENG Su-ping，MENG Zhao-ping，WANG Hu,et al.Testing study on pore ratio and permeability of sandstone under different confining pressures[J].Chinese Journal of Rock Mechanics and Engineering，2003，22(5)：742-746.

[12]张改玲，王雅敬.高围压下砂土的渗透特性试验研究[J].岩土力学，2014，35(10)：2748-2754.

ZHANG Gai-ling,WANG Ya-jing.Experimental investigation of hydraulic conductivity of sand under high confining pressure[J].Rock and Soil Mechanics，2014，35(10)：2748-2754.

[13]张天军，尚宏波，李树刚，等.分级加载下破碎砂岩渗透特性试验及其稳定性分析[J].煤炭学报，2016，41(5)：1129-1136.

ZHANG Tian-jun，SHANG Hong-bo，LI Shu-gang，et al.Experimental study on permeability characteristics of broken sandstones and its stability analysis under step loading[J].Journal of China Coal Society，2016，41(5)：1129-1136.

[14]孙明贵，黄先伍，李天珍，等.石灰岩应力-应变全应变过程的非Darcy流渗透特性[J].岩石力学与工程学报，2006，25(3)：484-491.

SUN Ming-gui，HUANG Xian-wu，LI Tian-zhen，et al.Seepage properties of non-darcy flow in complete failure process of limestone[J].Chinese Journal of Rock Mechanics and Engineering，2006，25(3)：484-491.

[15]李顺才，陈占清，缪协兴，等.饱和破碎砂岩随时间变形-渗流特性试验研究[J].采矿与安全工程学报，2011，28(4)：542-547.

LI Shun-cai，CHEN Zhan-qing，MIAO Xie-xing，et al.Experimental study on saturated and fractured sandstone deformation-seepage characteristics with time[J].Journal of Mining and Safety Engineering，2011，28(4)：542-547.

[16]王晓东.渗流力学基础[M].北京：石油工业出版社，2006.

WANG Xiao-dong.Seepage mechanics basis[M].BeiJing：Petroleum Industry Press，2006.

[17]但汉城，李亮，杨小礼，等.基于渗流理论的沥青路面渗入率计算与分析[J].中南大学学报，2010，41(2)：742-748.

DAN Han-cheng，LI Liang，YANG Xiao-li，et al.Calculation and analysis of infiltration rate of asphalt pavement based on percolation theory[J].Journal of Central South University，2010，41(2)：742-748.

[18]张天军，任金虎，陈占清，等.多种矿物成分破碎岩石渗透试验[J].辽宁工程技术大学学报，2014，33(4)：465-469.

ZHANG Tian-jun，REN Jin-hu，CHEN Zhan-qing，et al.Experimental study on the sermeability parameters of broken rock with various mineral composition[J].Journal of Liaoning Technical University，2014，33(4)：465-469.