利用GEK代理模型的天线快速多目标优化设计

王丹青， 李　萍

(武警工程大学 信息工程系，陕西 西安 710086)

多目标优化算法辅助的天线自动与半自动设计，能够综合考虑各项设计要求，获得最优天线结构．它降低了天线设计对工程经验的依赖，具有自动化、智能化的优点，是未来天线设计的必然发展趋势[1]．但由于优化过程中需要频繁调用电磁仿真软件进行仿真计算，算法的整体时间复杂度较大，难以适用于多参数复杂天线的设计．因此，提高优化效率，缩短天线优化时间成为研究热点．对此，部分学者在智能优化算法迭代寻优中调用计算成本低、仿真时间短的代理模型代替电磁仿真软件．代理模型是根据人工神经网络(Artificial Neural Network， ANN)[2-4]、克里金模型(Kriging Model， KM)[5-7]和多项式拟合模型(Polynomial Fitting Model，PFM)[8-10]等方法建立的天线结构参数与电磁性能响应间映射关系的近似模型．引入代理模型完成优化的时间成本包括代理模型建立和算法迭代寻优两部分．目前研究多侧重于通过减少建立代理模型所需样本数量[6，11-12，14]，缩短样本仿真时间[7，13]或两相结合的方法[8-10]来减小建立代理模型的时间成本．但由于仍采用传统的全局优化算法，迭代寻优收敛慢，优化效率不理想．

因此，笔者首先将遗传算子引入多梯度下降算法中，提出了混合遗传算子多梯度下降算法(Multi-Gradient Descent Algorithm hybrid with Genetic Operator， MGDA-GO)．该算法具有全局性好、寻优收敛速度快的优势．然后建立梯度增强型克里金(Gradient-Enhanced Kriging， GEK)模型[11]，作为MGDA-GO算法求解天线多目标优化设计问题中天线电磁仿真的代理模型．相较于一般克里金代理模型，GEK代理模型达到相同代理仿真准确度所需样本的规模较小．利用文中算法对加载各向异性Ⅰ型周期结构覆层的警用超短波宽带单极子天线和某型直升机机载双频超高频(Ultra High Frequency，UHF)专用通信天线的关键结构及以其为阵元的抗干扰阵列天线进行优化．与利用遗传算法调用仿真软件的优化方法相比，文中算法所需电磁仿真次数更少，优化时间更短，优化效率更高．

1　混合遗传算子多梯度下降算法

1.1　问题描述

多目标优化问题可以记为

(1)

其中，x=[x1，x2，…，xm]T，为m维优化变量;fi(x)(i=1，2，…，n)为n个优化目标函数;gi(x)和hi(x)分别为优化问题的不等式约束和等式约束条件．求解多目标优化问题所得解集称为非支配解集或Pareto最优解集，在目标函数空间中构成Pareto前沿(Pareto Front， PF)[12]．

1.2　算法描述

笔者在传统多梯度下降算法(Multi-Gradient Descent Algorithm， MGDA)[13]中引入遗传算子，提出混合遗传算子多梯度下降算法(MGDA-GO)．该算法首先由多维均匀拉丁超立方采样(Latin Hypercube Sampling with MultiDimensional Uniformity，LHS-MDU)[14]方法在设计空间中得到初代样本集；然后对其执行遗传算子，利用产生的子代种群初始化多梯度下降算法，并通过在迭代寻优中对产生的解执行遗传算子，避免算法过早陷入局部最优．MGDA-GO的具体步骤如下:

步骤1利用LHS-MDU方法采样得到初代样本集Gs=LHS(D，Dn)，其中，D为优化变量的维数，Dn为各维度上采样点的个数．初始化算法迭代次数t=0．

步骤2对Gt(G0=Gs)中的个体进行实数编码，根据轮盘赌法选择父代样本P1，P2∈Gt．然后生成随机数rc，比较其与交叉概率φ的大小．当rc<φ时，根据

(2)

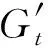
(3)

其中，d(xi(fj))的计算公式为

(4)

步骤4遍历非支配解集Nt，根据

(5)

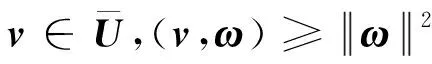
(6)

的梯度下降方向-ω．然后根据

maxH，H={h|∀ρ∈[0，h]，fi(x)≥fi(x-ρω)，1≤i≤n},

(7)

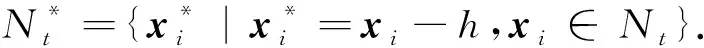
2　MGDA-GO调用GEK代理模型求解天线多目标优化问题

2.1　优化流程

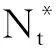
2.2　实例验证与分析

2.2.1加载各向异性Ⅰ型周期结构覆层的警用超短波宽带单极子天线的优化设计

图1　新型单极子天线结构示意图

利用文中算法对如图1所示的新型超短波单极子天线进行结构优化．该新型单极子天线是在传统单极子结构的基础上，新增两层内、外壁上均覆有各向异性Ⅰ型周期结构的套筒，与传统单极子同轴共置．Ⅰ型周期结构覆层的介质选择Rogers Ultralam 3850 (ε= 3.48，tanδ= 0.002 7) 材料，厚 0.51 mm．分析各向异性Ⅰ型周期结构单元的电磁特性，可知其介电常数在套筒与单极子的共同轴线方向上的分量较高．因此，通过优化调整各向异性Ⅰ型周期结构单元和加载周期结构覆层的套筒结构参数，能够在不影响其中同轴共置的传统单极子谐振的同时，产生另一谐振频率，从而拓展天线带宽．该天线优化问题可表示为

minU(R(x))=[U1(R(x))，U2(R(x))]．

(8)

优化变量包括新增各向异性Ⅰ型周期结构覆层的单元结构参数和传统单极子天线的长度h，记为x= [a，b，c，d1，h]T．优化目标函数可表示为

(9)

其中，U1为计算在设计要求的频段 (250～ 500 MHz) 內，采样频点fi(频率采样步长为 25 MHz，采样点总数为I)处天线反射系数S11的平均值;U2为计算天线样本体积(h1为各向异性Ⅰ型周期结构覆层的高度)．同时设置优化约束条件 max(S11(fi))≤ -10 dB，以去除优化中阻抗匹配不能满足实际使用要求的天线结构．

针对优化目标U1建立梯度增强型克里金代理模型，MGDA-GO调用代理模型求解该天线多目标优化问题，得到如图2所示的Pareto前沿．重复MGDA-GO求解该优化问题共5次，从每次所得的非支配解集中选出1个天线样本在HFSS软件中进行仿真验证．选中天线的结构参数见表1，仿真验证所得的反射系数曲线如图3所示．

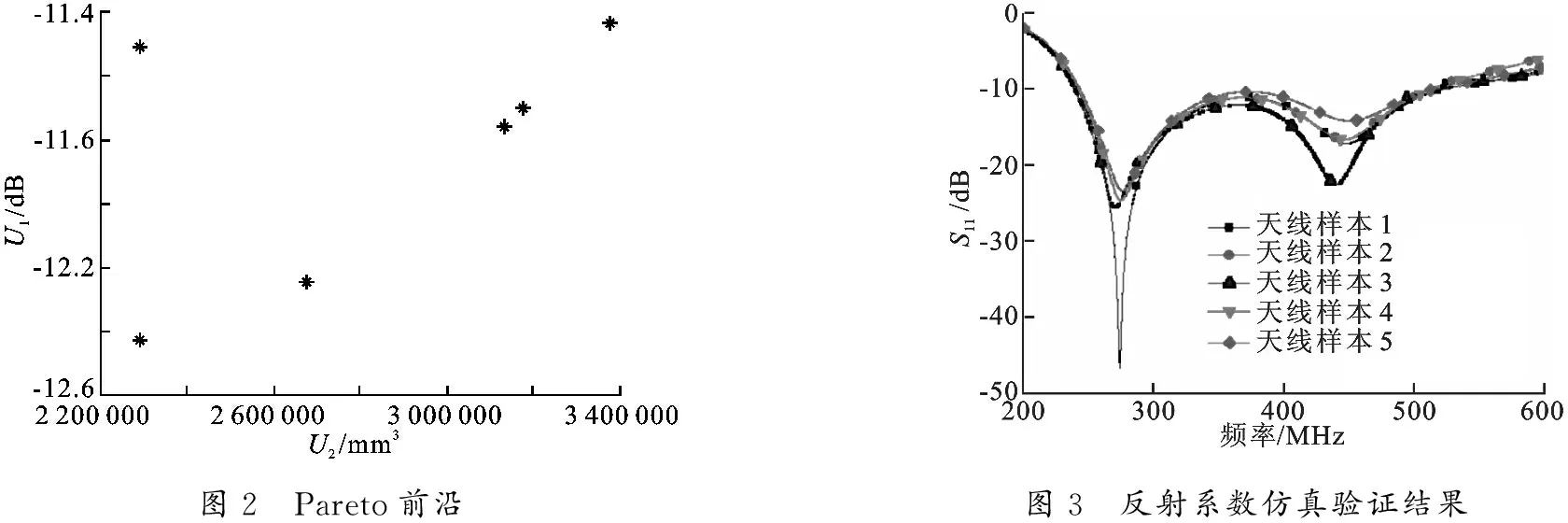
图2 Pareto前沿图3 反射系数仿真验证结果

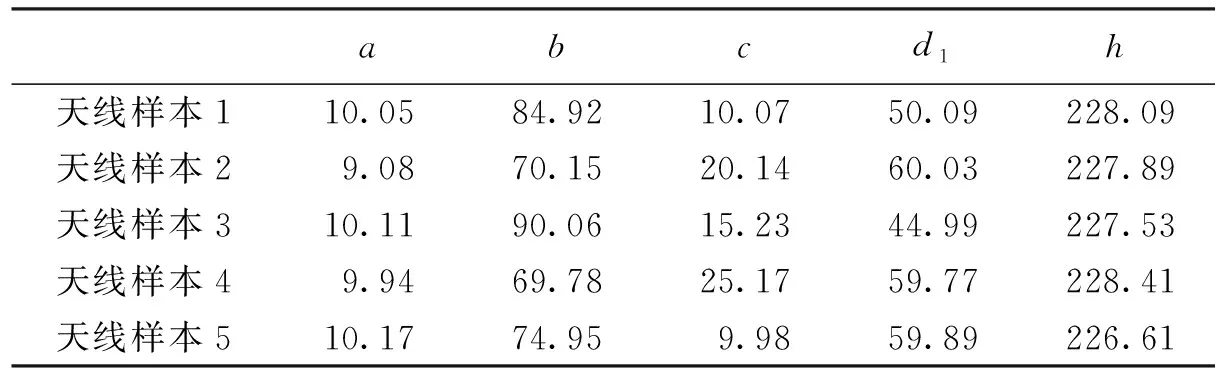
表1　优化天线结构尺寸 mm

利用文中优化方法求解该天线优化问题所需电磁仿真次数为139次(见表2)．利用文献[5]提出的由遗传算法调用克里金代理模型的天线优化方法求解该天线优化问题，重复优化实验5次，平均一次优化需要的电磁仿真次数为207次(见表2)，是利用遗传算法直接调用仿真软件(HFSS)的15.33%．对比可见，对于求解该天线优化问题，文中算法仅需文献[5]方法所需电磁仿真次数的67.15%，是利用遗传算法直接调用仿真软件进行优化所需电磁仿真次数的10.30%．

表2　优化时间成本对比

2.2.2机载UHF双频天线及其抗干扰阵列的优化设计

利用文中算法对某型直升机专用通信系统中的机载UHF双频天线进行优化设计．天线基本结构为平面单极子，通过在平面单极子旁引入窄条形寄生金属辐射体(以下称为金属前沿)，改变天线辐射体表面电流分布，使天线在低频段新增谐振频点．然后，在天线主辐射面上加载水平缝隙，提高天线在设计要求工作频段上的阻抗匹配性能，天线结构如图4(a)所示．该天线结构的优化问题可表示为

minU(R(x))=[U1(R(x))，U2(R(x))，U3(R(x))，U4(R(x))]．

(10)

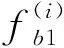
(11)

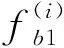
(12)

一个工作频段内的频率采样点总数为I，频率采样步长为5 MHz．

优化算法的求解过程重复6次，结合实际从各次优化所得非支配解集中选择天线样本(见表3)在HFSS仿真软件中进行验证．验证中参考机腹实际设置天线地板尺寸，得到反射系数曲线如图5所示．将文中优化算法的优化时间成本与利用非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-Ⅱ，NSGA-Ⅱ)调用电磁仿真的优化算法以及NSGA-Ⅱ调用克里金代理模型的优化方法进行对比，由表4所示的对比结果可得，文中优化算法所需的电磁仿真次数仅为其他两种方法的18.96%和57.66%．

表3　天线结构参数 cm

表4　优化时间成本对比

图4　天线结构

以优化所得天线样本1为单元，组成如图4(b)所示的 1×7 均匀直线抗干扰相控阵．利用文中优化算法MGDA-GO对阵元激励的幅度和相位进行优化，优化目标为阵列法线上主波束方向上增益最大，同时最大副瓣电平最小．图6给出了在仿真软件HFSS中按优化所得的天线阵列馈电方式之一: 阵元幅度为 0.845 9 W，0.805 4 W，0.627 2 W，0.507 4 W，0.348 6 W，0.214 1 W，0.113 6 W; 阵元相位为193.11°，197.75°，190.97°，198.38°，187.56°，208.91°，190.17°进行馈电时阵列的辐射方向图．可见，优化后阵列在 350 MHz 时全部副瓣均低于主波束增益 -15 dB 以上; 在 850 MHz 时主波束增益为 11.71 dB，副瓣电平均低于 -6.55 dB，阵列辐射良好，能够完成抗干扰通信任务，实现了既定的优化目的．

3　结 束 语

利用优化算法直接调用仿真软件进行天线优化的传统方法效率很低，针对这一问题，笔者首先通过在多梯度下降算法中引入遗传算子，提出了一种高效的全局优化算法——混合遗传算子多梯度下降算法(MGDA-GO)．并且建立梯度增强型克里金模型(GEK)代理天线的电磁仿真过程．MGDA-GO调用GEK代理模型计算优化目标函数完成寻优 ， 得到可供决策者灵活选择的Pareto最优解集 ． 利用文中算法分别优化了加载各向异性Ⅰ型周期结构覆层的警用超短波宽带单极子天线、某型直升机机载双频UHF专用通信天线及其抗干扰相控阵．上述实例中，文中优化算法所需的电磁仿真次数明显少于利用NSGA-Ⅱ调用电磁仿真软件的优化方法，提高了优化效率．文中算法对于各类天线及其他微波器件的优化设计均具有一定的借鉴意义．

图5 反射系数仿真验证结果图6 优化后阵列方向图

参考文献：

[1] NAGAR J, WERNER D H. A Comparison of Three Uniquely Different State of the Art and Two Classical Multiobjective Optimization Algorithms as Applied to Electromagnetics[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(3): 1267-1280.

[2]刘道华, 王淑礼, 薛瑞. 混合神经网络匹配响应面的多学科设计方法[J]. 西安电子科技大学学报, 2012, 39(5): 161-167.

LIU Daohua, WANG Shuli, XUE Rui. Multi-disciplinary Design Method for the Matched Response Surface Based on the Hybrid Neural Network[J]. Journal of Xidian University, 2012, 39(5): 161-167.

[3]KUMAR A, SHUKLA C K. Artificial Neural Network Employed to Design Annular Ring Microstrip Antenna[J]. International Journal on Computer Science and Engineering, 2012, 4(4): 556-564.

[4]AOAD A, SIMSEK M, AYDIN Z. Development of Knowledge Based Response Correction for a Reconfigurable N-shaped Microstrip Antenna Design[C]//Proceedings of the 2015 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization. Piscataway: IEEE, 2015: 7415078.

[5]陈晓辉, 裴进明, 郭欣欣, 等. 一种基于多维均匀采样与Kriging模型的天线快速优化方法[J]. 电子与信息学报, 2014, 36(12): 3021-3026.

CHEN Xiaohui, PEI Jinming, GUO Xinxin, et al. An Efficient Antenna Optimization Method Based on Kriging Model and Multidimensional Uniform Sampling[J]. Journal of Electronics & Information Technology, 2014, 36(12): 3021-3026.

[6]KOZIEL S, BEKASIEWICZ A, ZIENIUTYCZ W. Expedited EM-driven Multiobjective Antenna Design in Highly Dimensional Parameter Spaces[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13(1): 631-634.

[7]KOZIEL S, BEKASIEWICZ A. Fast Multi-objective Surrogate-assisted Design of Multi-parameter Antenna Structures through Rotational Design Space Reduction[J]. IET Microwaves, Antennas and Propagation, 2016, 10(6): 624-630.

[8]CHEN Y S, CHOU W H, CHEN S Y. Applications of Optimization Techniques to Designs of Ultra-wideband Planar Monopole Antennas[C]//Proceedings of the 2012 Asia-Pacific Microwave Conference. Piscataway: IEEE, 2012: 714-716.

[9]KOZIEL S, OGURTSOV S. Computational-budget-driven Automated Microwave Design Optimization Using Variable-fidelity Electromagnetic Simulations[J]. International Journal of RF and Microwave Computer-Aided Engineering, 2013, 23(3): 349-356.

[10]CHEN Y S. Multiobjective Optimization of Complex Antenna Structures Using Response Surface Models[J]. International Journal of RF and Microwave Computer-Aided Engineering, 2016, 26(1): 62-71.

[11]ULAGANATHAN S, COUCKUYT I, DHAENE T, et al. Performance Study of Gradient-enhanced Kriging[J]. Engineering with Computers, 2016, 32(1): 15-34.

[12] DEB K. Multi-objective Optimization Using Evolutionary Algorithms[M]. Chichester: John Wiley & Sons, 2001: 28-30.

[13]DÉSIDÉRI J A. Multiple-gradient Descent Algorithm(MGDA) for Multiobjective Optimization[J]. Comptes Rendus - Mathematique, 2012, 350(5/6): 313-318.

[14]DEUTSCH J L, DEUTSCH C V. Latin Hypercube Sampling with Multidimensional Uniformity[J]. Journal of Statistical Planning and Inference, 2012, 142(3): 763-772.

[15]ULAGANATHAN S, KOZIEL S, BEKASIEWICZ A, et al. Cost-efficient Modeling of Antenna Structures Using Gradient-enhanced Kriging[C]//Proceedings of the 2015 Loughborough Antennas and Propagation Conference. Piscataway: IEEE, 2015: 7366125.