多站雷达功率分配自修正凸松弛算法

冯涵哲， 严俊坤， 刘宏伟

(1. 西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071;2. 西安电子科技大学 信息感知技术协同创新中心，陕西 西安 710071)

在实际中，由于雷达平台的负载、能源等有限，多站分布式雷达系统在对目标进行定位时发射机总功率会受到相应的限制．近年来，已经有越来越多的学者开始研究如何使多站分布式雷达系统在有限资源约束下获取更好的目标定位跟踪性能和更长的工作时间[1-9]．功率分配是该类问题的一个重要子类，已得到国内外广泛研究[1，6-7，10-11]．功率分配在多个领域均有广泛应用．例如，在通信领域，对站点不足的区域，将距离信源较近的几个基站进行合理的资源优化，可以使有限的基站承担更多的通讯任务; 在互联网传输领域，由于每根网线传输速率有限，且不同服务器对所下载资料的贡献度不同，通过对距离较近的几个服务器资源进行分配，可提升下载速度．

多站分布式雷达功率分配最常见的方法是在其发射总功率恒定的前提下，通过调整各站的功率分布来提升目标定位精度．该方法可通过多种优化算法[1，6-7，10-11]快速获取优化结果．在多站分布式雷达背景下，文献[4，12]率先提出了针对目标定位的数学模型，并采用了凸松弛算法和域分解方法(Domain Decomposition Methods，DDM)对该模型进行优化．凸松弛算法操作简单，速度快，可直接通过CVX优化软件包得到解，编程方便，故目前非常流行．然而，凸松弛后模型的最优解与原问题模型实际最优结果之间存在一定的间隙，会引起额外误差．其中，间隙的大小、高度依赖于凸松弛参数的设定．而域分解方法则采用了一种类似于穷举搜索的贪婪算法的方法进行求解．该方法虽能准确求得最优解，但需花费大量时间进行优化．

针对上述两种算法所存在的缺陷，笔者在凸松弛算法的基础上提出了一种自修正的凸松弛算法．该方法首先采用传统的凸松弛模块对代价函数进行优化；然后，将所得到的结果进行处理，自修正凸松弛参数，经过多次迭代，逐步逼近域分解方法可以得到的理论最优解；最后，对提出的算法和已有的算法进行了有针对性的仿真实验，验证该算法在实际应用背景下的快速性和有效性．

1　数学模型

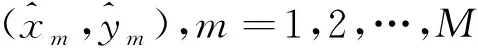
1.1　目标定位误差的克拉美罗界

如果噪声是方差为σω的高斯独立同分布，那么待估计变量u的误差先验条件概率密度函数可写为[13]

(1)

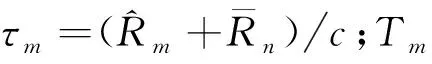
待估计变量u的著名费舍尔信息矩阵可表示为[14]

J(u)=E{[lnf(r|u)] [lnf(r|u)]H}．

(2)

式(2)代表似然函数梯度的协方差矩阵，可以导出克拉美罗下界(Cramér-Rao Lower Bound，CRLB)．

在文中，可调变量为多站分布式雷达系统各个发射站的发射功率pm，它们组成的矢量p= [p1，…，pM]．由于克拉美罗下界代表目标定位精度的下界，可以将其作为目标定位精度的衡量尺度．因此，现有工作大多将克拉美罗下界用作功率分配的代价函数[4-5]．在多站分布式雷达对目标定位时，误差的克拉美罗下界与费舍尔信息矩阵密切相关联，可表示为[5]

(3)

其中，J(u)是待估计变量u的费舍尔信息矩阵，tr(·)是矩阵的求迹运算．式(3)中，b= (d+e)，而A=deT-qqT． 其中，d= [d1，…，dM]T，e= [e1，…，eM]T和q= [q1，…，qM]T[15]:

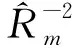
1.2　功率分配的优化问题和凸松弛后的优化问题

一旦得到了克拉美罗下界的函数表达式(3)，在总功率和单部雷达最大最小功率约束下，功率分配的优化模型可表示为

(7)

其中，IM=[1，1，…，1]T，是M×1矢量；Pmax和Pmin分别为每部发射雷达工作时的最大额定功率和最小待机功率．式(7)中约束是凸的，但目标函数是非凸非线性函数．因此，在优化过程中需要非线性搜索且可能存在局部最小点，求解难度较大．采用凸松弛技术[16]可以简化以上目标函数．

从式(7)的分式形式代价函数可以看出，其分子是线性函数，分母是凸二次型函数．通过将比值性的代价函数凸松弛为加性代价函数，可使其变为凸函数．凸松弛后，优化式(7)变为

(8)

其中，η是预先设定的自修正参数值．式(8)是典型的凸二次规划，采用CVX优化软件包来求解十分方便．

2　自修正凸松弛算法

从原理上来讲，自修正凸松弛算法就是在凸松弛算法的基础上，引入修正变量，对凸松弛参数进行校正来降低凸松弛引入的额外误差．该文以优化式(8)为基础，多次反馈修正参数以逼近最优解．

从式(4)～式(6)可发现，系统定位目标的精度与雷达的发射功率、距离方位信息以及目标的雷达散射截面等都有关． 式(8)是凸松弛为凸问题的优化模型，可以直接采用现今广泛使用的CVX优化软件包对其直接求解[5]．该算法的优点是求解过程简单，但凸松弛会引入额外误差．自修正凸松弛算法在凸优化的基础上引入了一种反馈校正的策略修正凸松弛引入的额外误差，具体算法如下．

自修正凸松弛算法的求解过程:

(2) 使用CVX优化软件包来求解式(8)的问题，得到凸松弛后优化结果pout．

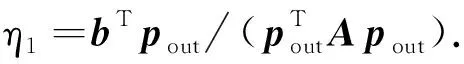
(4) 若|η1-η0|≤ε，(收敛条件取ε=10-8)，则停止迭代; 否则，令η0=η1，返回(2)，进行下一次的搜索循环．

总的来说，由上述算法可以快速简便地获取多站分布式雷达系统定位过程近似最优的资源分配方式．在模块化优化过程的同时，有效地减少了凸松弛带来的额外误差．

3　实验结果分析

为了验证笔者提出的算法在多基地雷达对目标定位的背景下能够有效、快速地修正凸松弛带来的额外误差，逼近最优功率分配，针对多站分布式雷达系统设计了一种目标定位仿真场景．将笔者提出的算法与凸松弛算法和域分解方法进行比较来验证其有效性．为简化仿真，实验中假设各部雷达发射参数相同，如表1所示．

表1　雷达发射信号参数

3.1　目标定位背景下不同算法优化性能比较

现有功率分配优化方法，如凸松弛算法和域分解方法[5]都存在缺陷．凸松弛算法求出的结果与实际最优解存在一定的额外误差;域分解方法采用的是一种贪婪算法，优化需要大量的计算时间．为了方便与这些算法进行性能对比，这里设计一种对目标联合定位的实验场景，通过该仿真来验证自修正凸松弛算法的优越性．图1给出了目标与雷达的空间位置分布示意图．

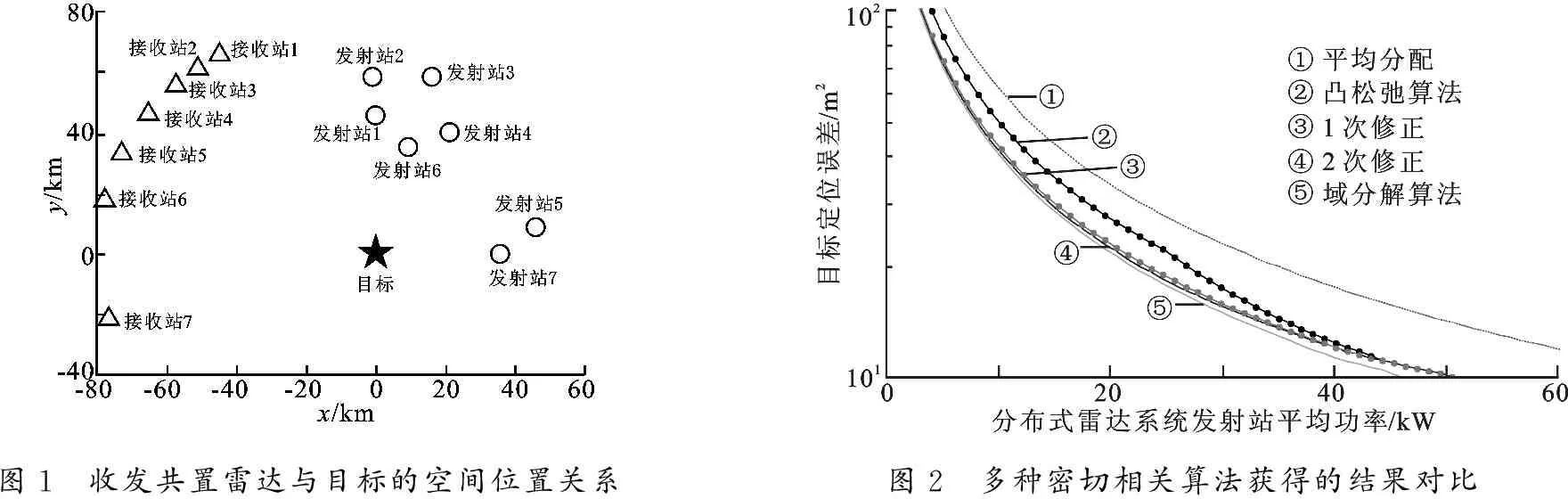
图1 收发共置雷达与目标的空间位置关系图2 多种密切相关算法获得的结果对比

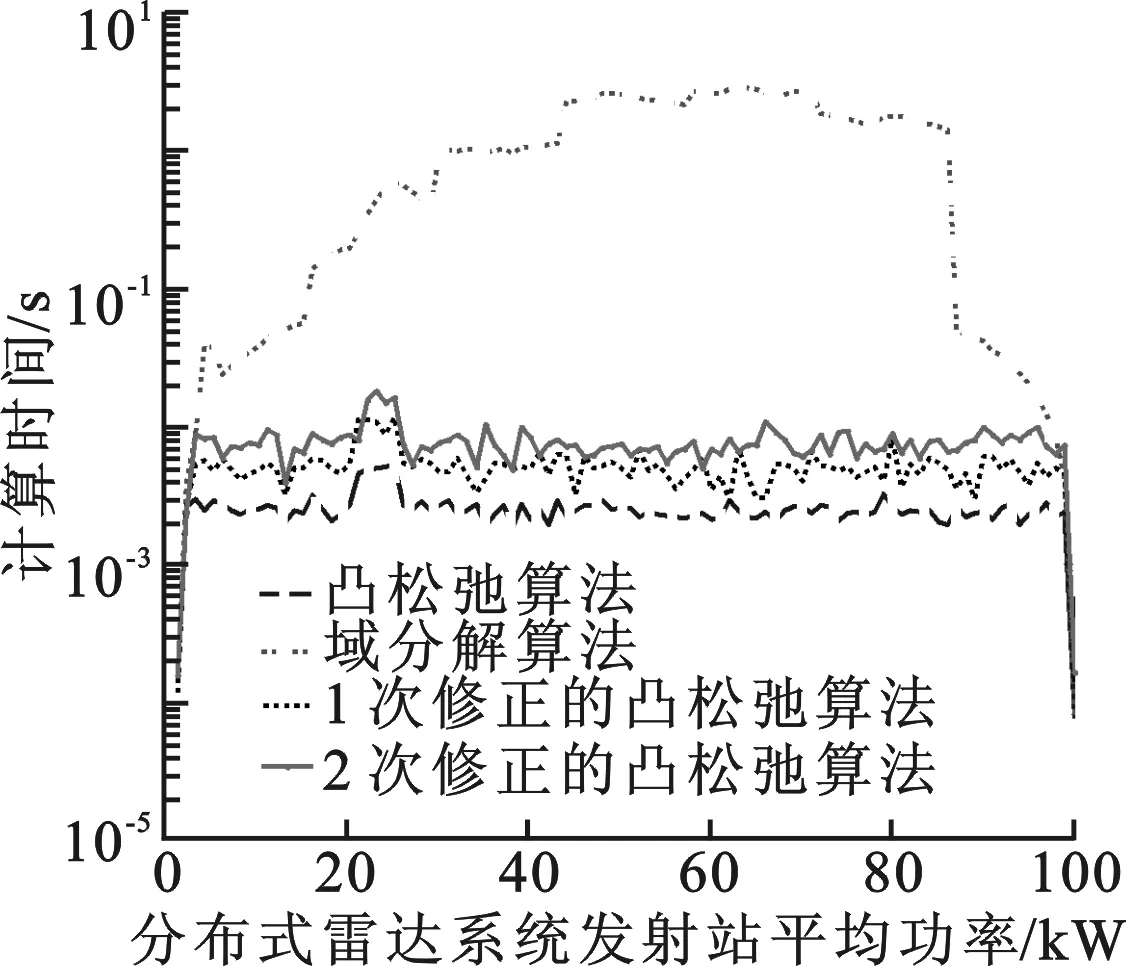
图3　多种算法计算时间对比

在不同的功率条件下，设定凸松弛参数η均为10．图2给出多种优化算法得出的定位精度．图2中的结果与理论分析一致，域分解方法能够获得最优的定位精度; 凸松弛算法因额外误差的引入只得到较差的定位精度; 修正凸松弛算法则能够有效地修正凸松弛带来的误差．值得注意的是，在大多数情况下，第1次修正明显减少了额外误差;在此之后的修正对额外误差的减少并不明显．图3给出了几种优化算法优化过程所需要的时间．从图2和图3中可以看出，自修正凸松弛算法因为修正过程要进行多次(2至3次)凸优化，所以计算时间相比已有凸松弛算法的要长，但还是远小于域分解方法所需的计算时间．因此，自修正凸松弛算法以少量计算时间的增加获得更好的性能．

3.2　不同凸松弛参数自修正凸松弛算法优化性能比较

为了显示凸松弛算法对凸松弛参数的高度依赖性，设计了如下实验，所有发射信号参数与表1相同，发射站、接收站和目标位置分布如图1所示．

该实验中，在不同凸松弛参数η0的条件下，比较了凸松弛算法对性能带来的损失以及修正后的效果．图4为η0取10条件下，采用凸松弛算法、域分解方法和自修正凸松弛算法分别获得的优化结果．图5为η0取1条件下，采用凸松弛算法、域分解方法和自修正凸松弛算法分别获得的优化结果．比较图4与图5可以看出，在参数为1的条件下，凸松弛算法性能损失远大于参数为10条件下进行的凸松弛算法．相应地 ， 在参数为1的条件下 ， 进行修正改进效果更加明显．

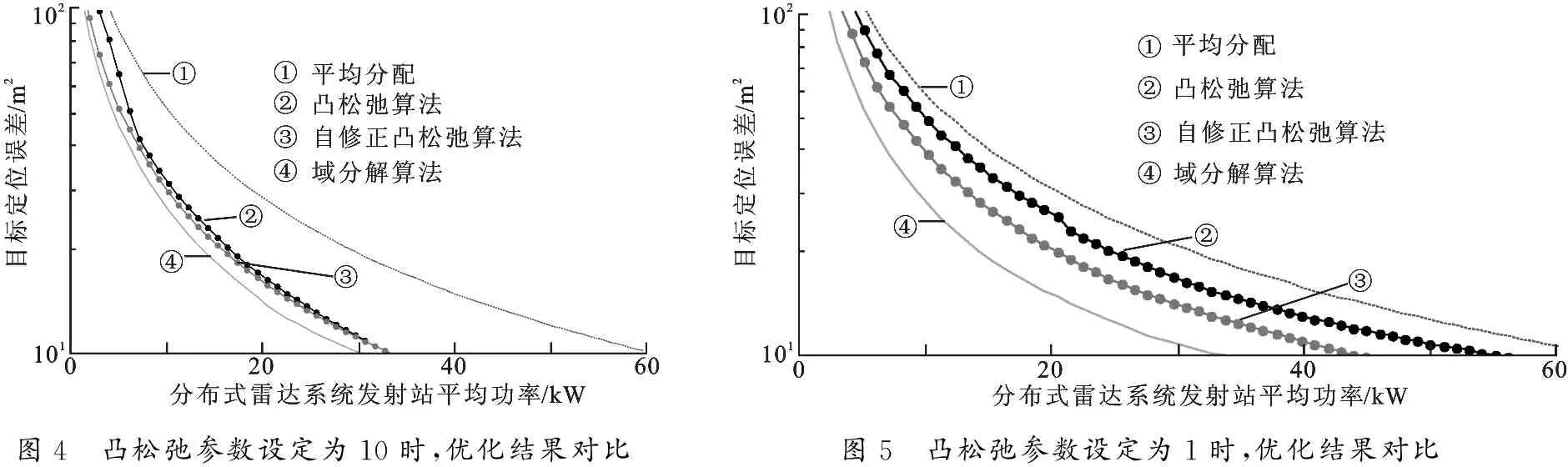
图4 凸松弛参数设定为10时,优化结果对比图5 凸松弛参数设定为1时,优化结果对比

该实验验证了凸松弛算法的性能损失高度依赖于凸松弛参数的设定，自修正凸松弛算法能够自适应地找到最优的凸松弛参数．

4　结 束 语

在多站分布式雷达系统下，笔者提出了一种可以采用CVX优化软件包的目标定位功率分配的自修正凸松弛算法．该算法能根据分布式组网雷达系统各部雷达的发射参数，在功率有限等约束下快速获取更好的定位性能．具体工作方式是在各个时刻，将功率尽可能地分配给优势雷达以对现有目标进行更好的定位．与传统的功率分配算法相比，笔者提出的算法优势如下:可以使用CVX优化软件包进行求解，便于软件编程和工程实际操作;通过反馈来修正凸松弛参数，有效地降低了凸松弛时引入的额外误差，优化结果接近最优结果．未来，将继续改进自修正凸松弛算法，并推广应用于分布式雷达目标跟踪检测等问题．

参考文献：

[1] GODRICH H, HAIMOVICH A M, BLUM R S. Target Localization Accuracy Gain in MIMO Radar Based System[J]. IEEE Transactions on Information Theory, 2010, 56(6): 2783-2803.

[2]FENG H Z, LIU H W, YAN J K, et al. A Fast Efficient Power Allocation Algorithm for Target Localization in Cognitive Distributed Multiple Radar Systems[J]. Signal Processing, 2016, 127: 100-116.

[3]YAN J K, LIU H W, JIU B, et al. Simultaneous Multibeam Resource Allocation Scheme for Multiple Target Tracking[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3110-3122.

[4]GODRICH H, PETROPULU A, POOR H V. Resource Allocation Schemes for Target Localization in Distributed Multiple Radar Architectures[C]//Proceedings of the 2010 European Signal Processing Conference. Poland: European Signal Processing Conference, 2010: 1239-1243.

[5]GODRICH H, PETROPULU A P, POOR H V. Power Allocation Strategies for Target Localization in Distributed Multiple-radar Architectures[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3226-3240.

[6]严俊坤, 刘宏伟, 戴奉周, 等. 基于非线性机会约束规划的多基雷达系统稳健功率分配算法[J]. 电子与信息学报, 2014, 36(3): 509-515.

YAN Junkun, LIU Hongwei, DAI Fengzhou, et al. Nonlinear Chance Constrained Programming Based Robust Power Allocation Algorithm for Multistatic Radar Systems[J]. Journal of Electronics & Information Technology, 2014, 36(3): 509-515.

[7]房嘉奇, 冯大政, 李进. TDOA中的修正牛顿及泰勒级数方法[J]. 西安电子科技大学学报, 2016, 43(6): 27-33.

FANG Jiaqi, FENG Dazheng, LI Jin. Research on Modified Newton and Taylor-series MEthods in TDOA[J]. Journal of Xidian University, 2016, 43(6): 27-33.

[8]SHI J N, JIU B, LIU H W, et al. Transmit Design for Airborne MIMO Radar Based on Prior Information[J]. Signal Processing, 2016, 128: 521-530.

[9]王海环, 王俊. 一种改进的多伯努利多目标跟踪算法[J]. 西安电子科技大学学报, 2016, 43(6): 176-182.

WANG Haihuan, WANG Jun. Multi-target Tracking with the Cubature Kalman Multi-bernoulli Filter[J]. Journal of Xidian University, 2016, 43(6): 176-182.

[10]SHI J N, JIU B, LIU Y, et al. Fast Transmit Waveform Design Method for Interference Mitigation in Simultaneous Multibeam MIMO Scheme[J]. Electronics Letters, 2016, 52(13): 1166-1168.

[11]STOICA P, SELéN Y. Cyclic Minimizers, Majorization Techniques, and the Expectation-maximization Algorithm: a Refresher[J]IEEE Signal Processing Magazine, 2004, 21(1): 112-114.

[12]GODRICH H, PETROPULU A, POOR H V. A Combinatorial Optimization Framework for Subset Selection in Distributed Multiple-radar Architecture[C]//Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE, 2011: 2796-2799.

[13]承德宝. 雷达原理[M]. 北京: 国防工业出版社, 2008.

[14]张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 2015.

[15] 肖海林, 王鹏, 聂在平, 等. 基于遗传算法的多基站协作通信功率分配方案[J]. 电子科技大学学报, 2014, 43(1): 26-30.

XIAO Hailin, WANG Peng, NIE Zaiping, et al. Power Allocation Scheme Based on Genetic Algorithm for Multi-base Station Cooperative Communication[J]. Journal of University of Electronic Science and Technology of China, 2014, 43(1): 26-30.

[16]STEPHEN B, LIEVEN V. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004.