联合频相估计中的对称化解耦合技术

孙锦华， 王　昊， 余忠洋

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室，陕西 西安 710071)

在同步接收机中，载波同步是整个通信系统中非常重要的一环，由收发信机晶体振荡器偏差及通信双方相对移动产生的多普勒频移效应引起的较大频率偏移会使得接收机解调和译码的性能急剧恶化．对于突发通信系统而言，同步模式、突发结构和估计算法都会对同步系统的性能产生至关重要的影响．为了实现较为理想的载波同步，首要工作就是选择同步模式．传统的同步模式分为数据辅助(Data-Aided，DA)和非数据辅助(Non-Data-Aided，NDA)两类[1]．DA同步模式是利用一段已知的导频序列通过线性去调制来获得包含载波参数的单音信号用于估计．NDA同步模式是利用非线性变换的方法进行去调制或是利用似然函数[2]、解调软信息或译码软信息辅助的方法进行同步．由于非线性变换的影响，NDA同步模式具有较高的信噪比(Signal-Noise-Ratio，SNR)门限和复杂度．在联合频相估计算法方面，文献[3]提出了一种针对跳频系统的联合相位估计和解调算法，文献[4]针对相干光正交频分复用(Coherent Optical Orthogonal Frequency Division Multiplexing, CO-OFDM)系统提出了一种联合数据辅助与相位盲搜索的相偏估计算法，两种算法均具有较高的相偏估计精度，但都没有考虑频偏(或剩余频偏)对相偏估计的影响．在突发通信的联合频相估计中，残留的剩余频偏很可能不为零甚至不可忽略，这将严重影响整个联合频相估计器的性能．文献[5-6]考虑了将接收端采样零时刻放置于突发结构正中间的情况，并分别给出了该情况与传统情况下联合频相估计的克拉美罗界(Cramer-Rao Bound，CRB)，但在实际运用中，并不可能人为地设置采样零时刻的位置，且文献[5-6]也没有进一步讨论这种结构对载波同步性能可能存在的影响．文献[7]作为本文的前期工作，针对突发通信的载波同步问题设计了一种通用的突发结构，并在此基础上推导了DA模式的载波参数估计性能界．

针对这些问题，在文献[7]已有工作的基础上，首先介绍了一种通用突发结构，并给出了基于该通用突发结构的载波相偏的估计性能界; 其次，从已有的估计性能界出发，提出了一种对称化解耦合技术(Symmetry Decoupling Technique，SDT)，并给出了SDT的理论分析和操作步骤; 再将该技术运用于联合频相估计的情况，并以最大似然(Maximum Likelihood，ML)算法为例分析了SDT对联合频相估计器的影响．最后，基于SDT提出了并行联合频相估计器，与传统的必须先估计频偏再估计相偏的估计器(文中称之为串行联合频相估计器)不同，该估计器可以在一定的频偏范围内并行地进行频偏估计和相偏估计．

1　信号模型与突发结构

为了与串行联合频相估计器的性能进行对比，考虑准静态平坦衰落信道下的单载波突发传输系统(系统的定时估计可以通过初始同步突发结构中的导频序列获得)．在上述条件下，接收端经过匹配滤波和采样后，经过能量归一化的等效基带离散信号可以表示为

r(k)=m(k) exp(j(2πkTν+θ))+w(k),k∈κSDT或κNSDT,

(1)

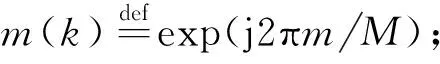
对于DA同步模式而言，将式(1)的两边同时乘以m(k)*(*表示取共轭)，便可以得到去调制信号; 而对于NDA同步模式，考虑针对MPSK类信号采用M次幂的非线性变换方法．为了统一后文中对两种同步模式的分析，这里将去调制信号统一表示为

z(k)=exp(j(2πkTν+θ)α)+ζ(k),

(2)

其中，ζ(k)为噪声项，其统计特性与w(k)相同，α为引入的同步模式选择因子．当采用DA同步模式时，α=1；当采用上面提到的NDA同步模式时，α=M．

图1　通用突发结构

文献[7]给出了DA同步模式下基于此通用突发结构的费舍尔信息矩阵(Fisher Information Matrix，FIM)，如果同时考虑利用未知数据块的情况，则FIM可扩展为

(3)

将κ1和κ2分别代入FIM，再对FIM求逆，即可得到DA同步模式和NDA同步模式下频偏和相偏估计的CRB．考虑后文需要，这里仅给出两种同步模式下载波相偏估计的CRB，即

(4)

2　对称化解耦合技术及其在联合频相估计中的应用

在上面CRB的推导过程中，假定了采样零时刻在该突发的起始处，即未经过SDT处理的情况，此时k∈κNSDT．在高信噪比的条件下，F(σ2)≈1[8]，则式(3)可以重新表示为

(5)

可以看到，此时FIM中非对角线上的元素的值受到k取值的影响．

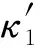
(6)

通过对比可以发现，运用SDT的FIM中，其非主对角线上的元素均为0．等价地，在对应的载波参数估计CRB中，频偏和相偏参数相互之间不会发生影响，即其载波频偏估计CRB和相偏估计CRB解耦合．

以图1中的任意一块导频或数据为例，给出对称化解耦合技术的具体步骤．这里统一用L表示其长度．首先需要对所取导频或数据块的长度L进行讨论．由于对称结构需要奇数个符号构成，当L为偶数时，可以只用其前L-1 个符号进行后续操作，这样既保证了结构的对称性，也不会损失太多的估计性能．故下面仅针对奇数个符号的情况进行讨论．

(7)

用式(7)对整个块内的符号进行相位旋转，得

(8)

图2　对称化解耦合技术示意图

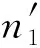
基于上述理论研究，现在考虑将SDT运用在联合频相估计中．前面的讨论从FIM和CRB出发，与具体的估计算法并无关系．而在实际的应用中，SDT对频偏估计算法和相偏估计算法也没有特殊要求．为方便起见，下面以ML算法作为载波相偏估计方案，分析SDT在DA和NDA两种同步模式下对联合频相估计的影响．

这里，估计器以图1所示的第1个导频块(对应于DA同步模式，此时L=L1)或第1个数据块(对应于NDA同步模式，此时L=M1)为例来估计载波频偏和相偏．估计过程如下:

首先，利用长度为L的序列通过式(2)得到去调制信号z(k)．然后，令

(9)

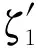
接着，基于ML估计器可获得相偏估计值，即

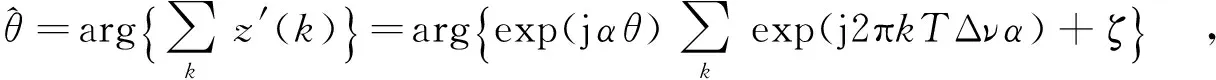
(10)

其中，ζ为一系列统计独立的噪声和．观察式(10)可以发现，NDA同步模式下的相偏估计不仅受到频偏的影响，还与调制阶数M有关．这是由于后者采用了非线性变换的结果．

为了与经过SDT处理的情况比较，首先讨论k∈{0，1，…，L-1}的情况．忽略噪声可得

(11)

其中，g(·)表示一个关于相偏和频偏的函数．由上式看出，未经过SDT处理时，若频偏不为零，则相偏估计值将偏离其真实值．

接着讨论经过SDT处理的情况，即k∈{-(L-1)/2，…，(L-1)/2}时，

(12)

其中，G(·)表示一个关于相偏和频偏的函数．可以发现，不论采用何种同步模式，当 |Δν|≤ 1/(αLT) 时，即使有频偏存在，相偏的估计值仍等于其真实值(或真实值的M倍)．所以，SDT可以降低联合频相估计中对频偏估计算法的精度要求，从而降低系统复杂度．

上面的讨论仅利用了图1所示突发结构中的第一个导频块或数据块，这里考虑将其推广到其他段或多段的情况．与第1块的情况相比，这种情况只是会多出一部分相位累计量，这是由于频偏经过时间的积累而造成的．这部分相位累积量可以一起作为待估计和补偿的相位偏差进行处理．需要指出的是，由于实际系统中的频率偏移可能很大(超过上述推导中的频偏范围)，故上述分析和操作更加适用于载波同步的细估计阶段．

至此，可以进一步对联合频相估计器的结构进行讨论．在传统的联合频相估计中，估计器必须先对频偏进行估计，然后才能对相偏进行估计，否则，叠加在信号上的频偏会导致后续相偏估计性能的严重恶化．将这种传统的估计器称作串行联合频相估计器．而如果将SDT引入联合频相估计中，便可以实现相偏估计和频偏估计的解耦合，即SDT可以让相偏估计和频偏估计同时进行．将这种估计器称作并行联合频相估计器，如图3所示．

图3　串行/并行联合频相估计器

3　仿真分析

SDT处理最主要的功效在于使得相偏估计不再依赖于频偏估计，且提高了相偏估计对抗剩余频偏的能力，而不会对频偏估计的性能有所改善，故这里仅从相偏估计期望、不同信噪比下的估计均方误差(Mean-Square Error，MSE)和不同剩余频偏下的估计MSE来进行仿真和分析，验证前文结论．其中，调制方式为正交相移键控(Quadrature Phase Shift Keying，QPSK)，DA同步模式中采用的导频长度L1=20，NDA同步模式中采用的数据长度M1=20．

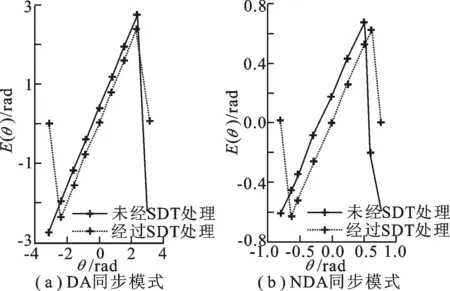
图4　不同相偏下的相偏估计期望

3.1　相偏估计期望

在DA模式的仿真中，假设相偏θ∈[-π，π]，频偏 Δν1= 0.01/T，信噪比Eb/N0= 10 dB．在NDA模式的仿真中，由于非线性去调制引入的调制阶数M的关系，NDA同步模式的相偏估计范围为DA同步模式的 1/M，故设相偏θ∈ [-π/4，π/4]，频偏 Δν2= 0.002 5/T．图4给出了不同相偏下的相偏估计期望．

可以看出，无论采用何种同步模式，在理论分析的相偏范围内，当存在频偏时，未经过SDT处理的相偏估计期望与相偏的真实值相异，从而导致相偏估计性能的恶化．而当频偏在式(12)所示的范围内时，经过SDT处理的相偏估计期望与相偏的真实值几乎完全重合．可预见，当频偏不为零时，SDT处理势必会改善相偏估计的性能．

3.2　不同信噪比下的相偏估计MSE

在DA同步模式中，假设信噪比 (Eb/N0)∈ [0 dB，10 dB]，相偏θ= 3π/4，频偏 Δν1= 0.01/T．在NDA同步模式中，相偏θ= π/6，频偏 Δν2= 0.002 5/T．仿真结果如图5所示．可见，当存在频偏时，两种同步模式下未经过SDT处理的相偏估计性能会变得非常差，而与之相比，经过SDT处理的相偏估计性能有较大的改善．需要说明的是，NDA模式由于引入了非线性去调制，从而使得其估计性能曲线逐渐靠近对应的CRB，而DA模式则不会出现这种“渐近”的现象．

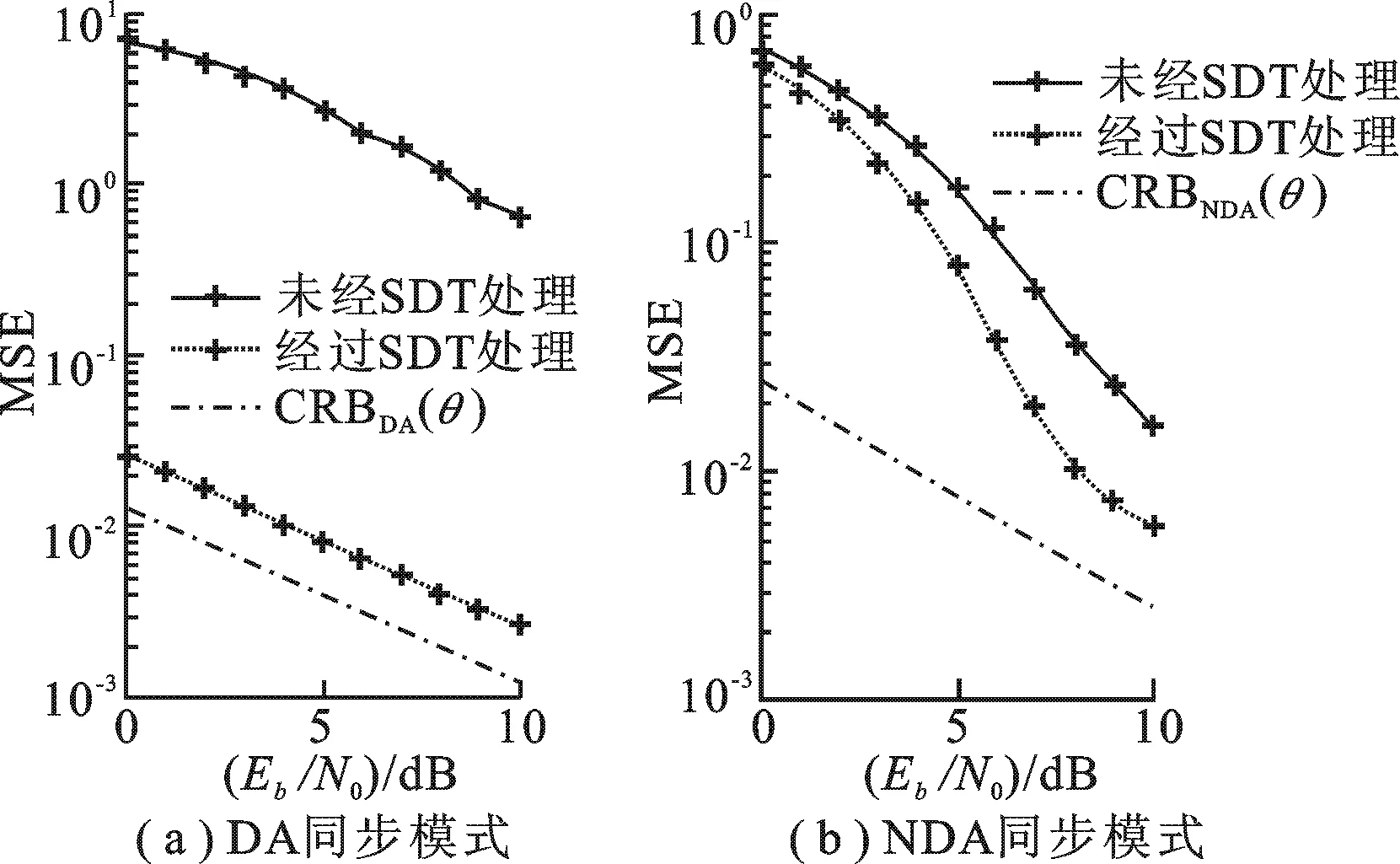
图5　不同信噪比下相偏估计的MSE

3.3　不同频偏下的相偏估计MSE

在DA同步模式中，假设频偏 Δν1∈ [-0.05/T，0.05/T]，相偏θ= 3π/4，信噪比Eb/N0= 10 dB; 在NDA同步模式中，假设频偏 Δν2∈ [-0.01/T，0.01/T]，相偏θ= π/6．图6给出了不同频偏下相偏估计的MSE．由图6可以看出，不论采用何种同步模式，传统的相偏估计对频偏的大小非常敏感; 而经过SDT处理的相偏估计可以在一定频偏存在的情况下完成对相偏的估计，这与式(12)的结论一致．这是由于SDT处理为频偏的累计引入了“抵消效应”，从而使得一定范围内的频偏不会对相偏估计产生影响．

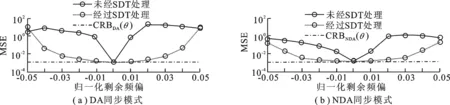
图6　不同频偏下相偏估计的MSE

4　结　　论

针对突发通信中的载波同步问题，提出了一种对称化解耦合技术，并将其引入到联合频相估计中，取得了较好的效果．理论分析和仿真结果均表明，无论采用DA或NDA同步模式，经过SDT处理的联合频相估计可以实现频偏估计和相偏估计的解耦合;与传统的相偏估计相比，经过SDT处理的相偏估计能够获得更高的估计精度和更强的对抗频偏(或剩余频偏)能力．此外，该对称化解耦合技术还适用于其他的联合频相估计方法，具有一定的普适性．

参考文献：

[1] MENGALI U, D’ANDREA A N. Synchronization Techniques for Digital Receivers[M]. Heidelberg: Springer, 1997.

[2]MASMOUDI A, LE-NGOC T. A Maximum-likelihood Channel Estimator for Self-interference Cancelation in Full-duplex Systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(7): 5122-5132.

[3]YIN Y, WU S, KUANG L L, et al. Tikhonov Sum Approach for Joint Carrier Phase Estimation and Decoding in Frequency-hopping Communications[C]//Proceedings of the 2015 International Conference on Wireless Communications and Signal Processing. Piscataway: IEEE, 2015: 7340983.

[4]CHEN R R, KUANG C X, ZHANG Z, et al. A Novel Pilot-aided and BPS Combined Phase Estimation Algorithm for CO-OFDM Systems[C]//Asia Communications and Photonics Conference Papers. Washington: OSA, 2016: AS3C.2.

[5]RICE F. Carrier-phase and Frequency-estimation Bounds for Transmissions with Embedded Reference Symbols[J]. IEEE Transactions on Communications, 2006, 54(2): 221-225.

[6]NOELS N, STEENDAM H, MOENECLAEY M, et al. Carrier Phase and Frequency Estimation for Pilot-symbol Assisted Transmission: Bounds and Algorithms[J]. IEEE Transactions on Signal Processing, 2005, 53(12): 4578-4587.

[7]YU Z Y, SUN J H, BAI B M, et al. A Phase Increment-based Frequency Estimator for General PSAM in Burst Communications[C]//Proceedings of the IEEE Vehicular Technology Conference. Piscataway: IEEE, 2016: 7504093.

[8]RICE F, COWLEY B, MORAN B, et al. Cramer-Rao Lower Bounds for QAM Phase and Frequency Estimation[J]. IEEE Transactions on Communications, 2001, 49(9): 1582-1591.