2个数值模式在昆明地区气温预报中的准确率比较

邹 阳，王 将

(云南省昆明市气象局，云南昆明 650034)

昆明市位于我国西南边陲、云贵高原中部，地处低纬高原，海拔高差悬殊，地形地貌复杂。气温随海拔增高而降低，垂直差异显著，高山寒，山区凉，坝区暖，河谷热。春季，受高空西风气流控制，天气晴朗，风力较大，干燥少雨，昼夜温差大；夏季，受西南季风和东南季风影响，多大雨、暴雨等强降雨天气，雨量集中，降雨量占全年的6成以上，无酷暑期；秋季，降温快，雨量比夏季减少5成多；冬季，日照充足，晴朗少雨，冷空气活动时会出现低温雨雪天气。非绝热加热、气温平流和垂直运动都是影响气温变化的因子，气温预报一直以来是天气预报的难点[1-2]。

目前，数值预报是天气预报的主要手段，屠妮妮等[3]对MM5及T639模式的2 m气温产品在不同区域进行检验，发现2个模式对不同区域的预报存在不同程度的误差，我国西部地区模式气温预报与实况近似程度低于中部及南部地区。蔡新玲等[4]对不同预报时效的MM5模式结果进行了检验并认为模式对气温预报存在系统误差。佟华等[5]认为气温误差是由于模式陆面过程所需初值的不科学性以及模式地形高度与实际地形高度存在较大差异造成的。蔡芗宁[6-7]、于超[8]认为ECMWF模式对各系统及要素的预报最接近实况；日本模式和T639模式次之。笔者将从不同气候带地区和不同季节2个方面对ECMWF和T639数值模式气温预报产品进行检验，了解2个数值模式在昆明地区的气温预报水平，为预报员今后能更好地应用2个数值模式气温预报产品提供可以借鉴的订正依据，增强应用数值预报产品的能力，提高昆明市气象局预报精细化水平。

1　资料与方法

1.1模式资料选取2012年2月29日—2013年2月27日ECMWF和T639数值模式08：00、20：00起报的24 h预报时效的850 hPa气温。ECMWF模式格距为2.5°×2.5°，T639模式格距为1°×1°。

1.2实况资料选取2012年3月1日—2013年2月28日昆明市12个县区国家气象站逐日最高、最低气温数据。

1.3检验方法由于2个模式的气温预报产品是分辨率不同的均匀分布的格点值，而昆明市12个县区国家气象站的气温实况值是不均匀分布的，因此，为了方便进行检验需要将模式格点资料插值到国家气象站上。插值方法采用双线性插值，又称为双线性内插。在数学上，双线性插值是有2个变量的插值函数的线性插值扩展，其核心思想是在2个方向分别进行一次线性插值。如图1所示，已知的空白正方形数据点与待插值得到的实心圆圈数据点。假如想得到未知函数f在点P= (x,y)的值，假设已知函数f在Q11= (x1,y1)、Q12=(x1,y2)、Q21=(x2,y1)、Q22=(x2,y2)4个点的值。首先利用公式(1)和公式(2)在x方向进行线性插值，得到R1和R2；然后利用公式(3)在y方向进行线性插值，得到P；这样就得到所要的结果f(x,y)。将2个模式20：00(08：00)起报的24 h预报时效的850 hPa气温作为模式预报的日最高(低)气温。由于选取的是ECMWF和T639数值模式的850 hPa气温预报值，因此采用胡林娜[9]和卜宪云[10]的方法将预报差值的平均值作为订正值，把模式预报值订正至2 m气温，表1为昆明国家气象站2个模式各月最高、最低气温订正值，同理可以得到昆明其他国家气象站2个模式各月最高、最低气温订正值。

图1　双线性插值示意Fig.1　Diagram of bilinear interpolation method

(1)

(2)

(3)

采用中国气象局下发的《中短期天气预报质量检验办法(试行)》〔2005〕109号文件中气温的平均绝对误差(TMAE)和预报准确率(TTK)检验方法，对2个模式在昆明地区2 m气温预报水平进行检验分析，计算公式如下：

(4)

(5)

其中，Fi为第i站(次)预报气温；Oi为第i站(次)实况气温；K为1、2，分别代表|Fi-Qi|≤1 ℃、|Fi-Qi|≤2 ℃；NrK为预报正确的站(次)数;NfK为预报的总站(次)数。

2　结果与分析

2.1昆明不同气候带地区的气温预报水平根据段旭等[11]最新的气候区划，云南大致可以分为6个气候带，即北热带、南亚热带、中亚热带、北亚热带、温带和高原气候带。昆明市共有12个县区，其中昆明主城区、安宁、晋宁、呈贡、嵩明、寻甸和太华山属于北亚热带，富民、宜良、石林和禄劝4个县区属于中亚热带，东川属于南亚热带。所以，将昆明主城区、安宁、晋宁、呈贡、嵩明、寻甸和太华山7个县区定义为北亚热带地区，富民、宜良、石林和禄劝4个县区定义为中亚热带地区，东川定义为南亚热带地区。为了了解2个数值模式对昆明不同气候带地区的气温预报水平，对2012年3月—2013年2月昆明12个县区国家气象站2个模式24 h的2 m日最高、最低气温预报产品进行准确率评分。

对比昆明地区不同标准的2 m日最高、最低气温24 h预报准确率(图2)发现，2个模式K=2 ℃(2 ℃误差)的预报准确率明显比K=1 ℃(1 ℃误差)的预报准确率有所提高，2 m日最高气温：ECMWF模式提高了25.8%，T639模式提高了28.2%；2 m日最低气温：ECMWF模式提高了26.9%，T639模式提高了29.2%。分别计算2个模式K=2 ℃标准的不同地区平均2 m日最高气温预报准确率，北亚热带地区：ECMWF模式为78.1%，T639模式为70.7%；中亚热带地区：ECMWF模式为75.3%，T639模式为70.1%；南亚热带地区：ECMWF模式为62.2%，T639模式为53.5%。所以，对于2 m日最高气温预报准确率来说，不同气候带地区均是ECMWF模式高于T639模式。分别计算2个模式K=2 ℃标准的不同地区平均2 m日最低气温预报准确率，北亚热带地区：ECMWF模式为74.0%，T639模式为83.8%；中亚热带地区：ECMWF模式为65.4%，T639模式为77.7%；南亚热带地区：ECMWF模式为65.2%，T639模式为59.8%。所以，对于2 m日最低气温预报准确率来说，北亚热带和中亚热带地区均是T639模式高于ECMWF模式；南亚热带地区ECMWF模式高于T639模式。从2012年3月—2013年2月ECMWF和T639模式不同气候带地区2 m日最高、最低气温平均绝对误差(图3)来看，与预报准确率的结论(图2)完全一致。

表1昆明国家气象站ECMWF、T639各月最高、最低气温订正值

Table1Correctedvalueonmaximum,minimumtemperatureofECMWFandT639modelsatKunmingstationindifferentmonths℃

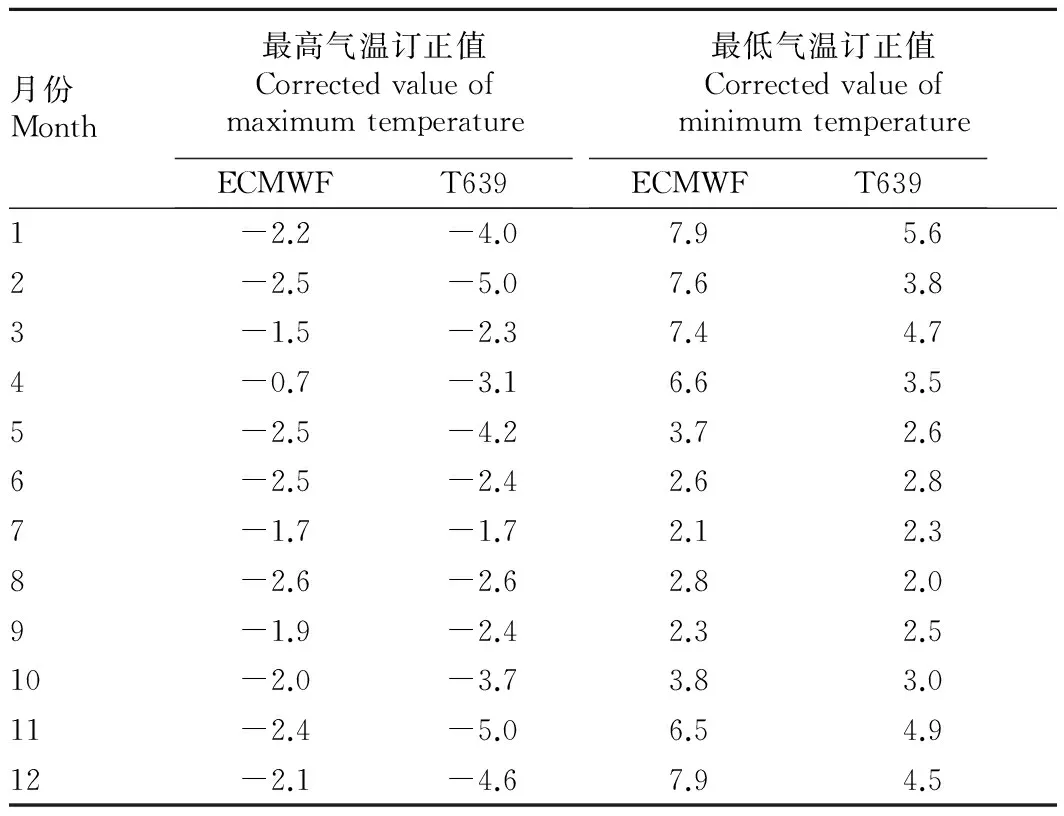
月份Month最高气温订正值CorrectedvalueofmaximumtemperatureECMWFT639最低气温订正值CorrectedvalueofminimumtemperatureECMWFT6391-2.2-4.07.95.62-2.5-5.07.63.83-1.5-2.37.44.74-0.7-3.16.63.55-2.5-4.23.72.66-2.5-2.42.62.87-1.7-1.72.12.38-2.6-2.62.82.09-1.9-2.42.32.510-2.0-3.73.83.011-2.4-5.06.54.912-2.1-4.67.94.5

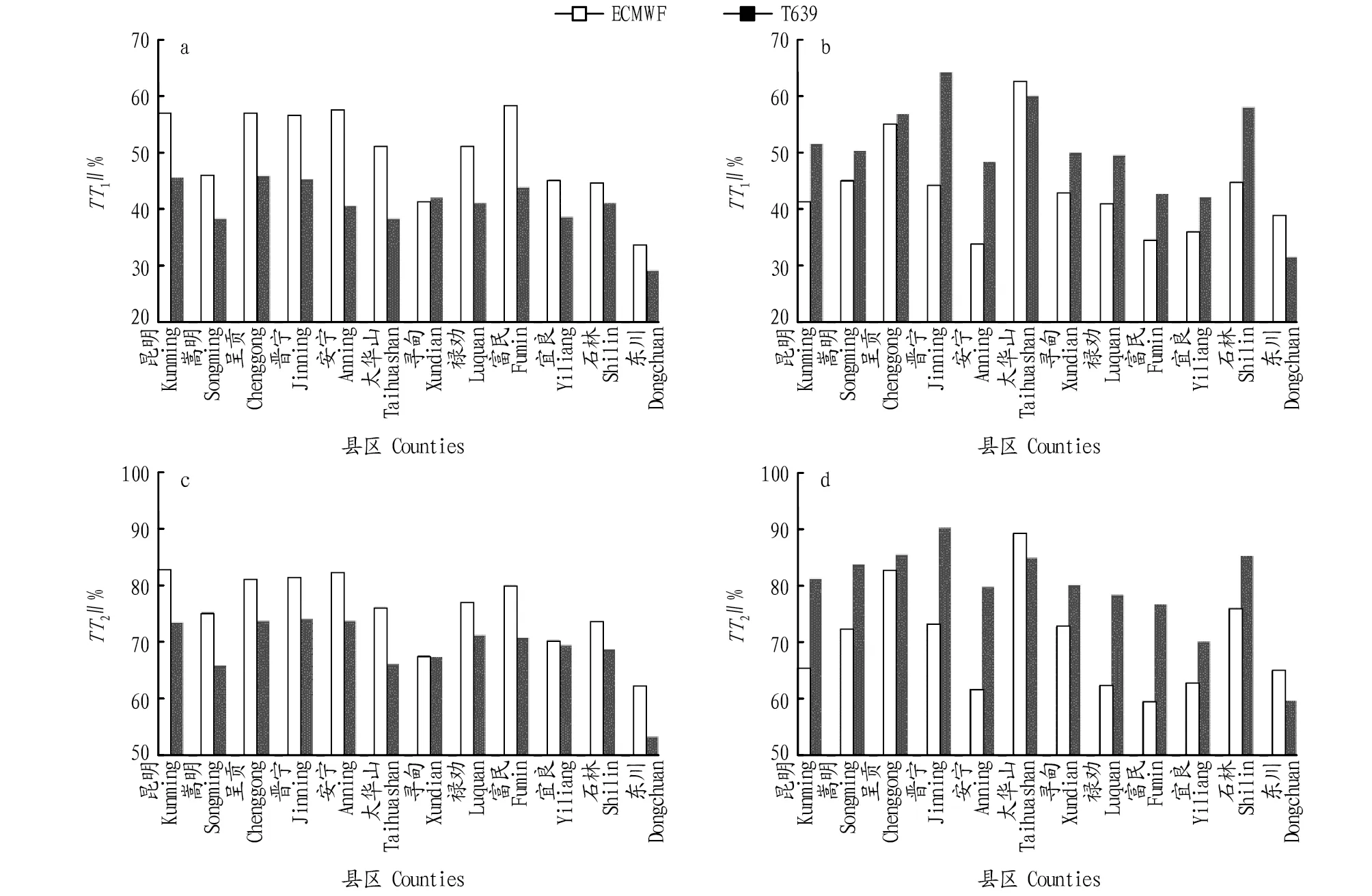
注：a.日最高气温，K=1 ℃；b.日最低气温，K=1 ℃；c.日最高气温，K=2 ℃；d.日最低气温，K=2 ℃Note:a.Daily maximum temperature,K=1 ℃;b.Daily minimum temperature,K=1 ℃;c.Daily maximum air temperature,K=2 ℃;d.Daily minimum air temperature,K=2 ℃图2　2012年3月—2013年2月不同标准不同气候带地区ECMWF和T639模式2 m日最高、最低气温24 h预报准确率Fig.2　Forecast accuracy of 2 meter daily maximum and minimum temperature of ECMWF and T639 models’ 24 h forecast products with different standards at different climate zone areas from March 2012 to February 2013

图3　2012年3月—2013年2月不同气候带地区ECMWF和T639模式2 m日最高(a)、最低(b)气温平均绝对误差(MAE)Fig.3　Mean absolute error of 2 meter daily maximum(a) and minimum(b) temperature of ECMWF and T639 models at different climate zone areas from March 2012 to February 2013

2.2昆明不同季节的气温预报水平根据气象上的划分法对四季进行划分：2012年3—5月为春季，2012年6—8月为夏季，2012年9—11月为秋季，2012年12月—2013年2月为冬季。计算不同季节2 m日最高、最低气温24 h预报准确率TT2。

从图4可以看出，春季，ECMWF模式预报准确率为63.0%～78.3%，T639模式预报准确率为57.8%～70.0%；除寻甸、宜良T639模式高于ECMWF模式(分别高7.0%和0.4%)外，昆明其他县区均是ECMWF模式高于T639模式，ECMWF模式比T639模式高4.1%～13.9%。夏季,ECMWF模式预报准确率为66.3%～82.6%，T639模式预报准确率为63.7%～80.2%;除安宁、太华山T639模式高于ECMWF模式(分别高0.8%和1.8%)外，昆明其他县区均是ECMWF模式高于T639模式，ECMWF模式比T639模式高0.3%～10.2%。秋季，ECMWF模式预报准确率为56.0%～86.8%，T639模式预报准确率为46.7%～83.3%；除安宁、太华山T639模式高于ECMWF模式(分别高0.8%和1.8%)外，昆明其他县区均是ECMWF模式高于T639模式，ECMWF模式比T639模式高0.3%～10.2%。冬季，ECMWF模式预报准确率为55.6%～92.2%，T639模式预报准确率为44.3%～77.3%；除寻甸T639模式高于ECMWF模式(高0.3%)外，昆明其他县区均是ECMWF模式高于T639模式，ECMWF模式比T639模式高0.8%～19.5%。分别计算不同季节2个模式昆明12个县区平均预报准确率发现，ECMWF模式预报准确率从高到低依次为秋季(78.6%)、冬季(78.2%)、夏季(75.2%)、春季(71.5%)，T639模式预报准确率从高到低依次为秋季(73.5%)、夏季(71.8%)、冬季(67.0%)、春季(64.0%)。

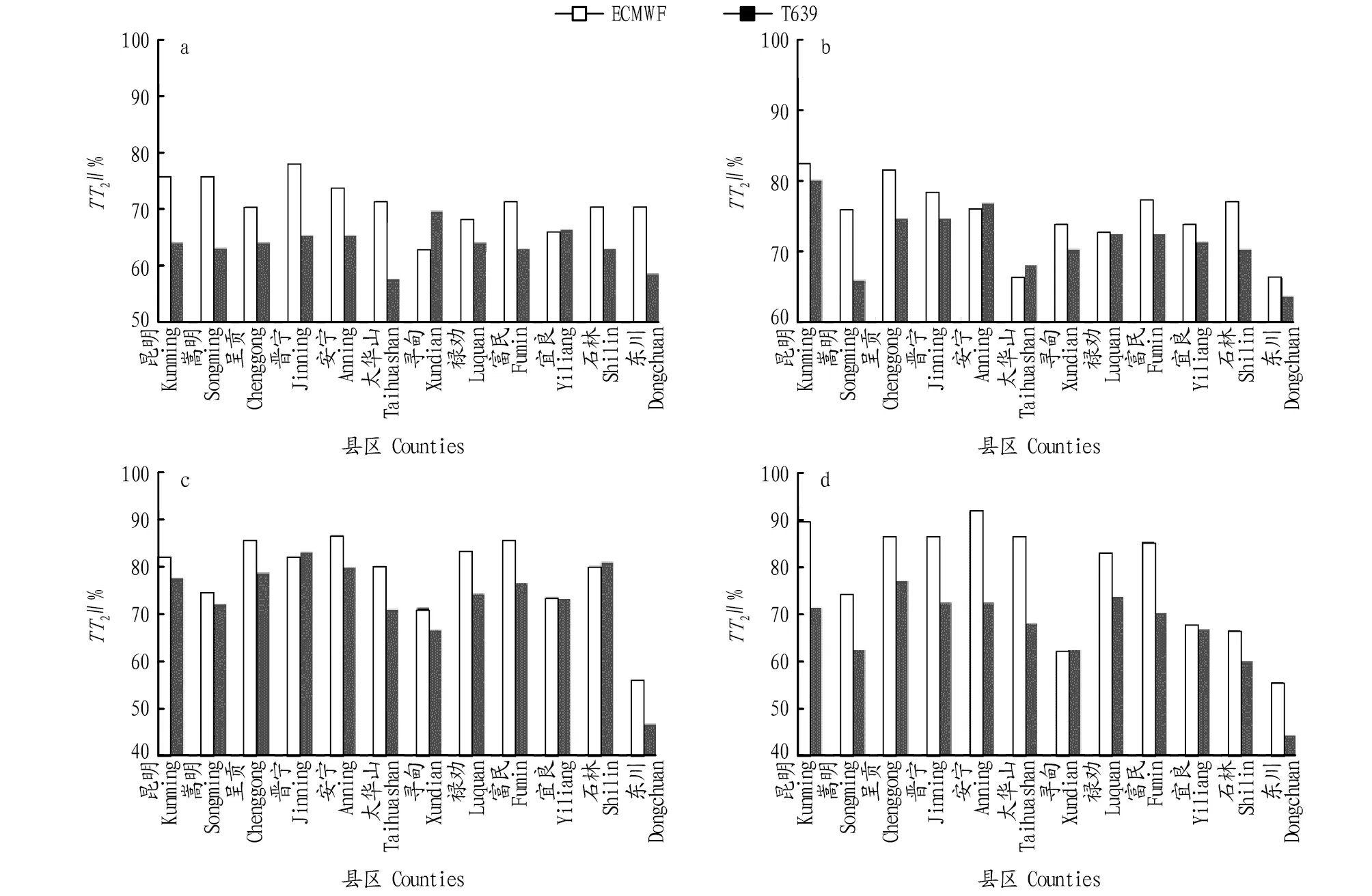
注：a.春季；b.夏季；c.秋季；d.冬季Note:a.Spring; b.Summer;c.Autumn;d.Winter图4　ECMWF和T639模式昆明12个县区不同季节2 m日最高气温预报准确率Fig.4　Forecast accuracy of 2 meter daily maximum temperature of ECMWF and T639 models at 12 stations in different seasons

从图5可以看出，春季，ECMWF模式预报准确率为52.2%～80.4%，T639模式预报准确率为45.1%～94.5%；除东川ECMWF模式高于T639模式(高14.7%)外，昆明其他县区均是T639模式高于ECMWF模式，T639模式比ECMWF模式高0.9%～29.1%。夏季，ECMWF模式预报准确率为81.5%～100.0%，T639模式预报准确率为80.5%～98.9%；除呈贡、太华山和东川ECMWF模式高于T639模式(分别高1.4%、2.3%和1.0%)外，昆明其他县区均是T639模式高于ECMWF模式，T639模式比ECMWF模式高0.8%～10.7%。秋季，ECMWF模式预报准确率为54.9%～91.2%，T639模式预报准确率为62.5%～89.8%；除太华山和东川ECMWF模式高于T639模式(分别高1.4%和0.9%)外，昆明其他县区均是T639模式高于ECMWF模式，T639模式比ECMWF模式高6.5%～16.7%。冬季，ECMWF模式预报准确率为43.3%～85.6%，T639模式预报准确率为41.4%～87.4%；除呈贡、太华山和东川ECMWF模式高于T639模式(分别高5.3%、14.3%和4.2%)外，昆明其他县区均是T639模式高于ECMWF模式，T639模式比ECMWF模式高6.7%～25.2%。分别计算不同季节2个模式昆明12个县区平均预报准确率发现，ECMWF模式预报准确率从高到低依次为夏季(92.7%)、秋季(67.6%)、春季(63.8%)、冬季(57.1%)，T639模式预报准确率从高到低依次为夏季(95.2%)、秋季(78.0%)、春季(67.0%)、冬季(64.0%)。

3　结论

(1)ECMWF和T639数值模式2 m日最高、最低气温2 ℃误差的预报准确率明显比1 ℃误差的预报准确率高。

(2)分析ECMWF和T639模式对昆明不同气候带地区的气温预报水平发现，2 m日最高气温预报准确率不同气候带地区都是ECMWF模式高于T639模式；2 m日最低气温预报准确率北亚热带和中亚热带地区均是T639模式高于ECMWF模式，南亚热带地区ECMWF模式高于T639模式。

(3)分析ECMWF和T639模式对昆明不同季节的气温预报水平发现，2 m日最高气温ECMWF模式预报准确率从高到低依次为秋季、冬季、夏季、春季，T639模式预报准确率从高到低依次为秋季、夏季、冬季、春季；2 m日最低气温ECMWF和T639模式不同季节预报准确率趋势相同，从高到低依次为夏季、秋季、春季、冬季。

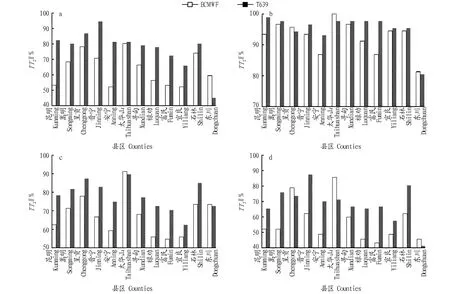
注：a.春季；b.夏季；c.秋季；d.冬季Note:a.Spring; b.Summer;c.Autumn;d.Winter图5　ECMWF和T639模式昆明12个县区不同季节2 m日最低气温预报准确率Fig.5　Forecast accuracy of 2 meter daily minimum temperature of ECMWF and T639 models at 12 stations in different seasons

[1] 赵声蓉.多模式温度集成预报[J].应用气象学报,2006，17(1):52-58.

[2] 赵斌华,汤光华,李力.某场站温度预报初探[J].应用数学,2004(S2):139-143.

[3] 屠妮妮,何光碧,张利红.成都区域气象中心业务数值预报产品检验分析[J].高原山地气象研究,2010,30(1):21-28.

[4] 蔡新玲,贺皓,高红燕，等.中尺度数值预报模式输出产品温度和相对湿度的检验[J].陕西气象,2006(1):4-8.

[5] 佟华,姚明明,王雨，等.T213L31全球中期数值天气预报系统2 m温度预报误差源分析[J].气象,2006,32(2):52-57.

[6] 蔡芗宁.2009年9—11月T639、ECMWF及日本模式中期预报性能检验[J].气象,2010,36(2):130-135.

[7] 蔡芗宁.2010年3—5月T639、ECMWF及日本模式中期预报性能检验[J].气象,2010,36(8):106-110.

[8] 于超.2010年6—8月T639、ECMWF及日本模式中期预报性能检验[J].气象,2010,36(11):104-108.

[9] 胡林娜.最高最低气温预报中的“温差订正法”[J].江西气象科技,1995(2):39-40.

[10] 卜宪云.日本传真图FXFE782中温度预报的检验与应用[J].辽宁气象,1996(1):11-12.

[11] 段旭,陶云,段长春.云南省细网格气候区划及气候代表站选取[J].大气科学学报,2011,34(3):336-342.