土壤垂向分层和均匀处理下水分差异的数值探讨*

熊丁晖, 刘苏峡**, 莫兴国

(1. 中国科学院地理科学与资源研究所陆地水循环及地表过程重点实验室 北京 100101; 2. 中国科学院大学 北京100049)

土壤水分是一种重要的水资源, 是联系地表水与地下水的纽带, 是水循环过程中不可缺少的成分,它和农业、水文、环境等领域有着密切关系。同时土壤水分是控制陆面与大气相互作用的一个重要变量[1]。不同复杂程度的陆面过程模型对土壤水分的准确模拟关系到陆-气间水平衡和水交换的模拟结果, 因此土壤水分的定量描述显得十分重要[2]。

在现有众多的陆面过程模型中, 对土壤水分的定量描述是通过以下两个方面来实现的[3]: 1)在垂向分布均匀的介质基础上, 基于 Richards方程来描述土壤水分的流动; 2)赋以地表土壤不同的水文特征和热力学特征。然而现实中土壤质地的垂向非均匀分布是很常见的。虽然目前部分陆面过程模型在水分的模拟上通过分层来刻画土壤的非均匀性, 但是对于大部分陆面过程模型而言, 一般是假设垂向均匀分布, 取表层土壤质地来表示整个垂向土壤质地。通过垂向均匀方式得到的土壤水分和实际垂向非均匀情况下的土壤水分存在差异, 这种差异有多大目前少有研究。

为了分析垂向均匀和垂向非均匀两种情况下的土壤水分差异, 本文建立一维土壤水分运动模型,对垂向均匀土壤和垂向非均匀土壤的水分运动进行数值模拟。考虑到模拟整个区域的非均匀土壤的水分运动将是一个繁重的工作, 为了简化工作, 本文选择3组不同饱和导水率组合的层状土壤代表不同区域的非均匀土壤, 取 3组层状土壤的上层土壤代表整个均匀土壤, 应用本文建立的一维土壤水分运动模型分析这 3组层状土壤和均匀土壤的水分差异, 以此来评价土壤垂向分层和均匀两种处理方式的差别。

1 研究方法

1.1 一维土壤水分运动模型

为了同时要模拟层状土壤和均匀土壤的水分运动过程, 建立一维层状土壤水分运动模型。土壤水分运动常采用Richards方程来描述, 对于层状土壤,由于层间界面处基质势是连续的, 而含水率是不连续的, 故选用以基质势h为因变量的Richards方程作为该土壤剖面水流运动的控制方程[4], 考虑作物根系吸水的Richards方程可表示为:

式中:h为基质势(cm);C为土壤比水容量(cm-1);K为土壤导水率(cm·d-1);t为时间(d);z为垂直坐标,方向向下为正(cm)。

作物根系吸水项选择中等复杂程度的 Molz-Remson线性模型[5]进行描述, 该模型假设根系吸水强度在土壤剖面上线性递减, 最大值在土壤表面,最小值在根系下边界, 并且进一步假定根系吸水在根系剖面上按 4∶3∶2∶1的模式分配, 具体表达为:

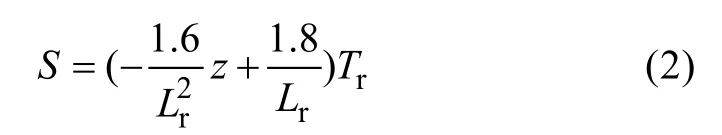
式中:S为根系吸水率(cm3·cm-3·d-1),Lr为有效根层深度(cm),Tr为作物蒸腾量(cm),z为地表以下深度(cm)。

本文采用隐式有限差分法对Richards方程进行数值差分, 由于层状土壤各层的水力参数不同, 结点设置有两种方法[6], 一种是顶点中心(vertex-centered, VC)方式, 一种是单元中心(cell-centered, CC)方式。本文选择顶点中心方式, 在层间界面处设 1个结点, 层间界面及两侧参数的计算公式为[7]:

式中:i为层间界面处的结点记号,K1、C1和K2、C2分别为层间界面处上下两侧的土壤导水率和土壤比水容量,hi-1、hi和hi+1分别为i-1结点、i结点和i+1结点处的基质势,Ki-1/2为i-1结点处土壤导水率和i结点处土壤导水率的几何平均值,Ki+1/2为i结点处土壤导水率和i+1结点处土壤导水率的几何平均值。

差分过程中, 假设t时刻的土壤剖面基质势已知, 求t+1时刻的土壤剖面基质势。土壤剖面离散为n个单元, 沿垂直方向结点编号为i=0, 1, 2, …,n,经处理得到一组三对角型方程组, 这种类型的方程组可用“追赶法”进行求解[4], 最后求解出t+1时刻土壤剖面所有结点的基质势, 再根据θ(h)关系式可以得到相应的土壤含水量。

时间步长Δt以天(d)为单位, 根据迭代次数进行自动调整, 调整规则如下[8]:

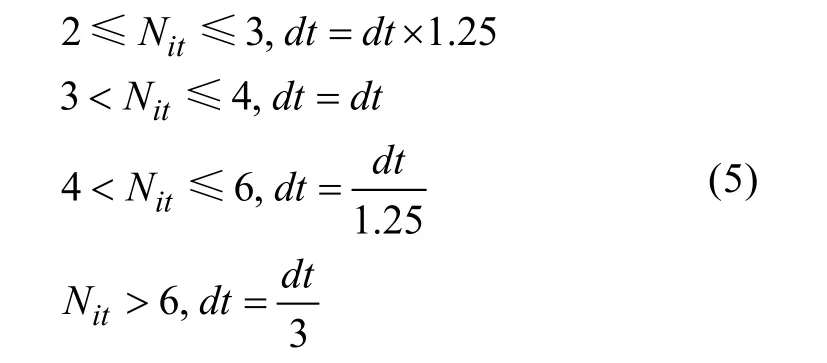
式中:Nit为t时刻求解土壤基质势的迭代次数。

使用 Fortran 90语言对上述差分方程进行编程求解, 程序设计流程图见图1。

1.2 一维土壤水分运动模型验证数据

为了对本文建立的一维土壤水分运动模型的可靠性进行验证, 本文采用了两套数据, 一套是Srivastava和 Yeh[9]提出的解析解, 另一套是中国科学院地理科学与资源研究所开展的室内五水转化试验, 详细介绍如下。

1.2.1 Yeh解析解

Srivastava和Yeh提出的解析解(简称Yeh解析解)是采用 Gardner函数作为土壤水力函数, 对Richards方程进行线性化得到的, 该解析解描述的是两层土壤的水流过程。Srivastava和Yeh根据解析解得到两组层状土壤的基质势分布, 该基质势分布被用来验证本文模型的可靠性。该层状土壤每层均为 1 m, 上边界条件为稳定降雨入渗, 入渗强度为0.9 cm·h-1, 下边界条件为自由水面, 这两组层状土壤上下层对应的 Gardner函数的水力参数值和初始基质势根据文献[9]进行确定。Yeh解析解设置的两组层状土壤的示意图见图2。

1.2.2 室内五水转化试验

室内五水转化动力过程试验(简称“室内五水转化试验”)装置位于中国科学院地理科学与资源研究所陆地水循环及地表过程重点实验室, 该装置大小为5 m×7 m×7.5 m(土壤表层以上高度为4.5 m, 土壤表层以下深度为 3 m), 由 3个子系统构成, 即环境要素控制子系统、土壤水分转化观测子系统和地下水控制子系统, 详细介绍见参考文献[10]。

选择室内五水转化试验2014年5月17日至9月19日层状土壤的水分数据, 层状土壤共3层, 第1层深度为0～100 cm, 第2层深度为100～210 cm, 第3层深度为210～300 cm, 地下水位精确设定在250 cm深度处。该层状土壤10 cm、33 cm、43 cm、53 cm深度处的实测土壤含水量数据被用于一维层状土壤水分运动模型的验证。

采用改进的van Genuchten-Mualem模型[11]描述土壤水分特征曲线和土壤导水率, 需要确定的参数包括饱和导水率(Ks)、饱和含水量(θs)、残余含水量(θr)、土壤孔隙大小参数(α)、形状参数(n)和经验参数(hs), 其中hs取为-1 cm, 其他参数值见表1。

对2014年5月17日不同深度处的土壤含水量进行线性插值得到初始土壤含水量。该试验的上边界条件为日蒸发量和灌溉量(图3), 下边界条件为自由水面。

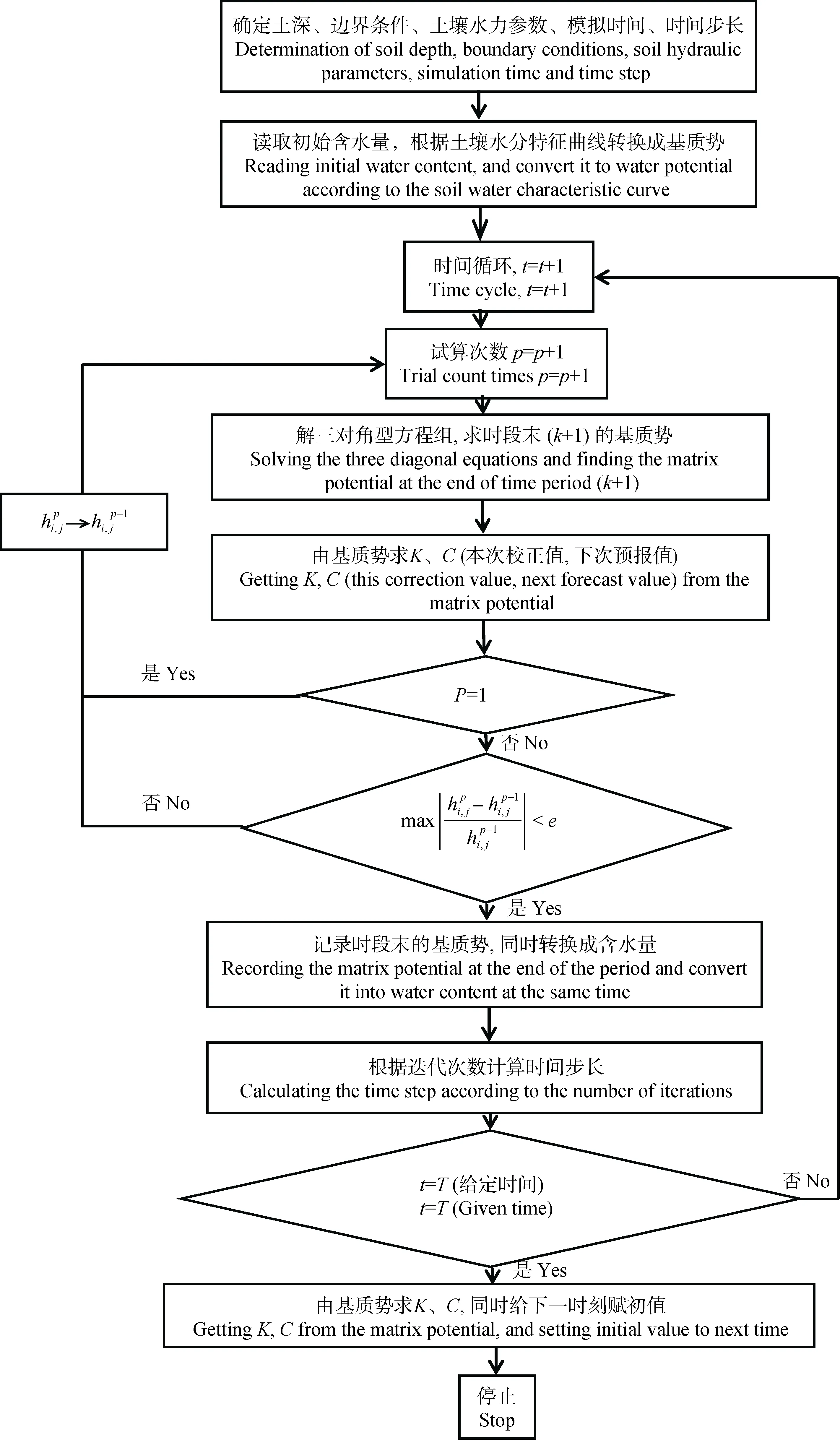
图1 一维土壤水分运动模型程序设计流程图Fig. 1 Flow chart of procedure design of one dimensional soil water movement model

因为室内五水转化试验没有测量有效根层深度,所以本文采用已有文献研究成果[13]:

式中:t为玉米生长日期(d),T为玉米生育期总天数(d),Lr(t)为有效根层深度(cm)。

1.3 土壤垂向分层和均匀处理数值试验方案

采用数值试验方案探讨土壤垂向分层和均匀处理下土壤水分的差异。考虑到区域土壤垂向的多样性, 设置 3组不同饱和导水率组合的层状土壤代表不同区域的非均匀土壤, 取 3组层状土壤的上层土壤代表整个均匀土壤。

图2 Yeh解析解设置的两组层状土壤示意图Fig. 2 Schematic diagram of two groups of stratified soils set by Yeh analytical solution

每组层状土壤均为两层, 上下层深度均为50 cm。采用改进的van Genuchten-Mualem模型描述土壤水分特征曲线和土壤导水率, 需要确定的参数包括饱和导水率(Ks)、饱和含水量(θs)、残余含水率(θr)、孔隙大小分布参数(α)和形状参数(n)和经验参数(hs)共 6个参数, 其中hs取为-1 cm, 各组的其他上下层土壤水力参数值见表2。

3组层状土壤的初始条件和上边界条件借用室内五水转换试验的数据, 即初始条件由基质势给定,上边界条件由蒸散发和灌溉给定, 层状土壤深度设置为100 cm, 下边界条件设置为自由排水边界。应用本文建立的一维土壤水分运动模型, 对上述 3组层状土壤和均匀土壤进行模拟, 得到土壤水分分布、渗漏量和储水量。

表1 室内五水转化动力过程试验层状土壤不同深度处的土壤水力参数值Table 1 Soil hydraulic parameters at different depths of the stratified soils at Water Transformation Dynamical Processes Experimental Device (WATDPED)

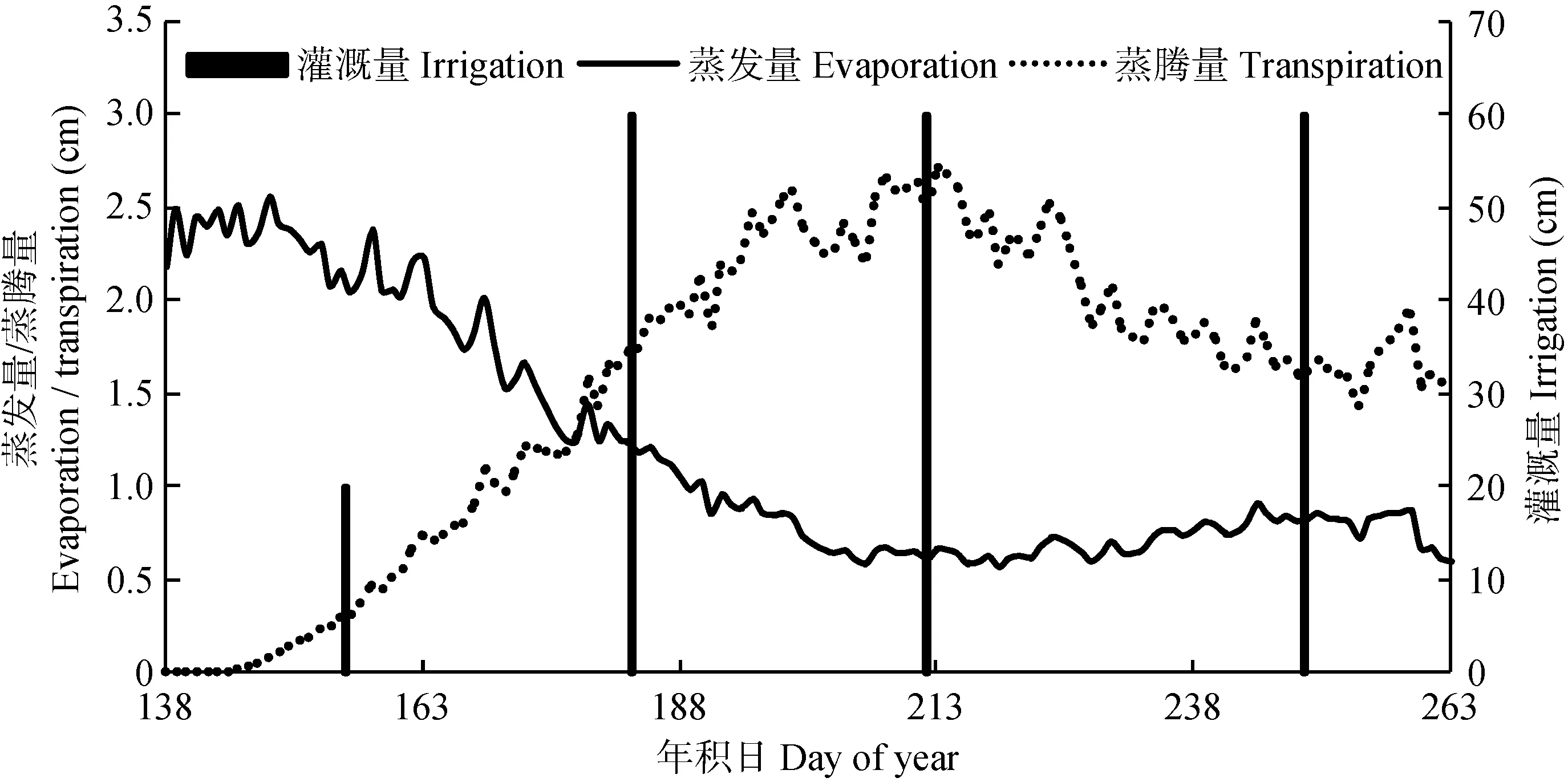
图3 室内五水转化试验夏玉米生育期内蒸发量、蒸腾量和灌溉量Fig. 3 Evaporation, transpiration and irrigation of summer maize measured at Water Transformation Dynamical Processes Experimental Device (WATDPED)

表2 3种饱和导水率组合的垂向分层土壤和均匀土壤(以上层土壤代表)处理数值试验的土壤水力参数值Table 2 Soil hydraulic parameters for the numerical experiments of stratified soils under 3 hydraulic conductivity combinations and homogenous soils (represented by the upper layer soil)

1.4 土壤水力参数敏感性分析

为了分析土壤水力参数对土壤垂向分层和均匀处理下的土壤水分差异的影响程度, 选择第 1组层状土壤和均匀土壤的渗漏量和储水量的差异为变量,在层状土壤下层水力参数不变的情况下, 分析层状土壤上层饱和导水率(Ks)、饱和含水量(θs)、残余含水率(θr)、孔隙大小分布参数(α)和形状参数(n)5 个参数的敏感性, 即在其他参数不变、单个参数增减10%的情况下, 通过考察渗漏量和储水量的变化, 分析这5个土壤水力参数的敏感性。第1组层状土壤上层原始水力参数值和增减 10%的土壤水力参数值见表3。

表3 土壤水力参数敏感性试验方案Table 3 Schemes for soil hydraulic parameter sensitivity analysis

土壤渗漏量计算采用达西定理，用最底层的负压水头梯度乘以水力传导度获得。土壤储水量的计算参见文献[14]。土壤渗漏量和储水量的差异用相对误差来表示, 相对误差的计算公式为:

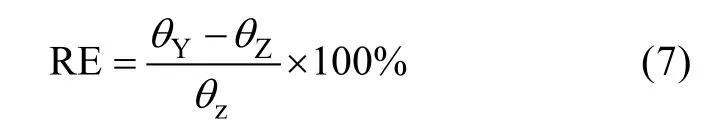
式中: RE为相对误差,θY为均匀土壤对应的渗漏量或储水量,θZ为层状土壤对应的渗漏量或储水量。

2 结果与分析

2.1 一维土壤水分运动模型的验证

2.1.1 Yeh解析解验证结果

根据Yeh解析解设置的两组层状土壤的初始条件、上下边界条件和土壤基质势分布, 对本文建立的一维土壤水分运动模型进行验证。模型设置时间步长为1 min, 空间步长为1 cm, 运行100 h, 得到两组层状土壤的基质势分布图, 和 Yeh解析解得到的基质势分布图进行比较, 见图4。

图4 第1组(a)和第2组(b)层状土壤剖面基质势的解析解(实线)和模拟值(虚线)Fig. 4 Analytical (solid lines) and simulated (dashed lines) soil matric potentials of the stratified soil group one (a) and group two (b)

图4展示了Yeh解析解和模型模拟得到的两组层状土壤基质势分布, 实线代表 Yeh解析解, 虚线代表模拟值, 横坐标表示土壤基质势h(cm),h=0表示土壤达到饱和, 纵坐标表示土壤深度z(cm),t=0 h表示初始时刻。图4a展示了第1组层状土壤基质势分布在t=0 h, 0.1 h, 0.5 h, 1 h, 2 h, 5 h, 10 h, 15 h, 20 h, 30 h, 50 h, 75 h, 100 h的模拟值和解析解, 其中t=75 h和t=100 h重合在一起, 图4b展示了第2组层状土壤基质势分布在t=0 h, 0.1 h, 1 h, 3 h, 6 h, 10 h, 15 h, 20 h, 30 h, 40 h, 50 h, 100 h的模拟值和解析解。结果显示两组层状土壤剖面基质势的模拟值和Yeh解析解几乎完全重合在一起, 说明本文建立的一维土壤水分运动模型在不考虑根系吸水的情况下能够正确模拟层状土壤水分运动过程, 同时也说明本文建立的一维土壤水分运动模型具有一定的可靠性。

2.1.2 室内五水转化试验验证结果

为了进一步验证本文建立的一维土壤水分运动模型在考虑根系吸水情况下的可靠性, 根据室内五水转化试验数据, 对一维土壤水分运动模型进行再次验证。模型设置初始时间步长为1 min, 后面根据迭代次数进行自动调整, 空间步长为 1 cm, 运行126 d。使用室内五水转化试验测量的未经率定的土壤水力参数, 得到的模拟值和实测值相差偏大。通过对土壤水力参数进行多次手动调参, 得到 1组相对合理的参数, 见表4, 应用这组参数进行重新模拟,得到不同深度处的土壤含水量分布图, 和实测值进行比较, 见图5。

表4 室内五水转化动力过程试验率定参数值Table 4 Calibrated parameters at Water Transformation Dynamical Processes Experimental Device (WATDPED)

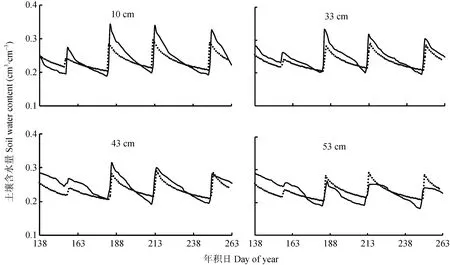
图5 室内五水转化动力过程试验层状土壤10 cm、33 cm、43 cm、53 cm深度处剖面含水量的实测值(实线)和模拟值(虚线)Fig. 5 Simulated (dashed line) and measured (solid line) soil moistures of the stratified soils at 10 cm, 33 cm, 43 cm and 53 cm depths at the Water Transformation Dynamical Processes Experimental Device (WATDPED)

图 5横坐标表示夏玉米生育期天数, 纵坐标表示土壤含水量(cm3·cm-3)。从图5中可以直观地看出,10 cm、33 cm、43 cm和53 cm处的土壤含水量模拟值和实测值很接近, 模拟值基本上能够准确捕获土壤水分的峰值(灌溉引起)、趋势走向(蒸散发引起)的特征, 表明本文建立的一维土壤水分运动模型能够用于考虑根系吸水的层状土壤水分运动模拟, 同时也再次说明本文建立的一维土壤水分运动模型是可靠的。

2.2 土壤垂向分层和均匀处理下的水分差异

为了分析土壤垂向分层和均匀处理下的水分差异, 应用建立的一维土壤水分运动模型, 对设置的3组不同饱和导水率组合下的层状土壤和对应的均匀土壤进行模拟, 得到土壤水分剖面图(图6)、土壤渗漏量随时间变化图(图 7)和土壤储水量随时间变化图(图 8)。

从图 6可以看出, 第 1组层状土壤上下层饱和水力传导度相差最小(1.5倍), 层状土壤和均匀土壤的剖面水分分布最接近(差别小于 0.05 cm3·cm-3);第 3组层状土壤上下层饱和水力传导度相差最大(3.3倍), 层状土壤和均匀土壤的剖面水分分布差距最大(差别达 0.15 cm3·cm-3左右)。这说明如果一个区域的土壤上下层饱和导水率相差较大的话, 那么垂向均匀处理会导致较大的误差, 这会严重影响土壤水分的准确估计, 在实际处理中需要认真考虑。

此外, 从图 6还能直观地看到, 层状土壤下层含水量远高于均匀土壤下层含水量。一方面是因为上边界条件主要是由蒸发驱动引起, 均匀土壤水分更容易被蒸发往上吸走; 另一方面是因为均匀土壤下层水力参数要大于层状土壤下层水力参数,导致均匀土壤的下层水流速度更快, 水分随时间减小更快。

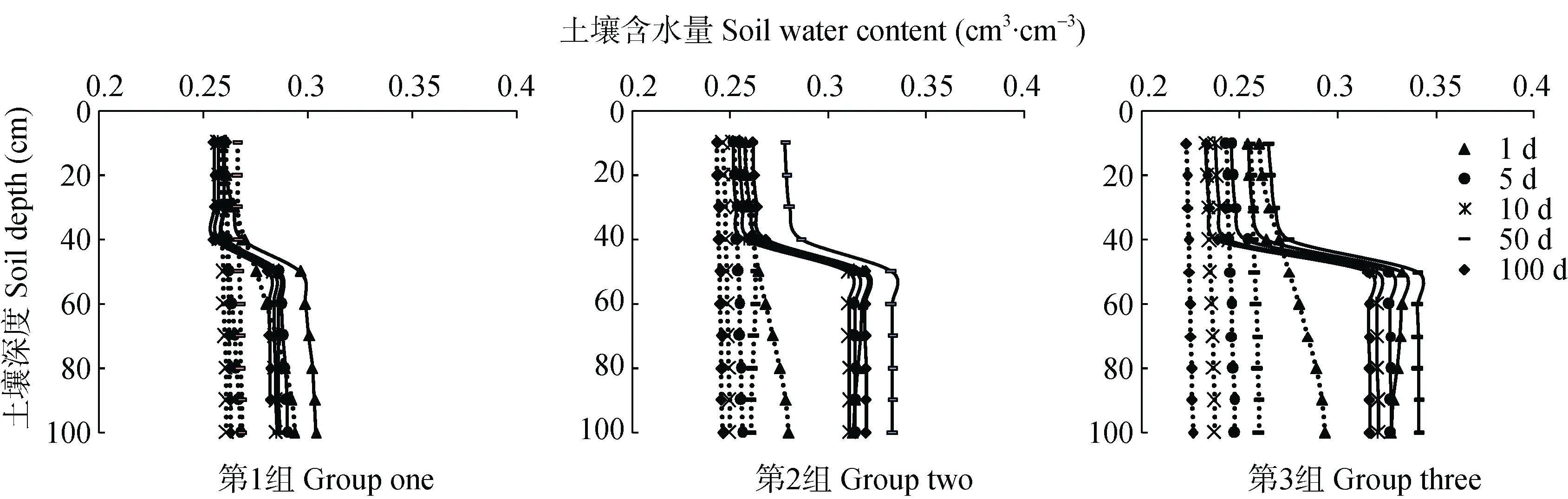
图6 3种饱和导水率组合下层状土壤(实线)和均匀土壤(虚线)不同时间的剖面水分分布Fig. 6 Soil water distribution profiles of layered (solid lines) and homogeneous (dashed lines) soil at different times under different hydraulic conductivity combinations

从图7可以看出, 3组层状土壤和均匀土壤的渗漏量均随时间递增。第 1组层状土壤和均匀土壤的渗漏量相差最小(几乎重合), 第2组和第3组层状土壤和均匀土壤的渗漏量在时段后期相差较大(达 20 cm以上)。

从图8中可以看出, 3组层状土壤和均匀土壤的储水量均随时间波动变化, 第 1组层状土壤和均匀土壤的储水量相差较小(相差2 cm左右), 而第3组层状土壤和均匀土壤的储水量相差较大(相差 5 cm左右)。

从上述结果可以看出, 3组不同土壤饱和导水率组合下的层状土壤和对应的均匀土壤的水分分布、渗漏量和储水量, 都是第1组差异较小, 而第3组差异较大。这表明对于上下层饱和导水率相差越大的层状土壤, 采用垂向均匀方式处理, 会导致各个水文变量的差异变大, 这在实际应用中需要特别注意。

图7 3种饱和导水率组合下层状土壤(实线)和均匀土壤(虚线)渗漏量随时间的变化Fig. 7 Water seepage of stratified soil (solid lines) and homogeneous soil (dashed lines) at different times under 3 hydraulic conductivity combinations

2.3 土壤水分参数的敏感性分析

为了讨论土壤水力参数包括饱和导水率Ks、饱和含水量θs、残余含水量θr、孔隙大小分布参数α和形状参数n这5个参数对土壤垂向分层和均匀处理下水分差异的影响, 本文以第1组层状土壤为例,采用第1组层状土壤和均匀土壤的渗漏量和储水量的相对误差作为评价参数敏感性的目标变量, 分别对层状土壤上层饱和导水率(Ks)、饱和含水量(θs)、残余含水率(θr)、孔隙大小分布参数(α)和形状参数(n)这5个参数值增减10%, 进行敏感性分析。这5个参数对土壤渗漏量和储水量的相对误差的敏感性分别见图9和图10。

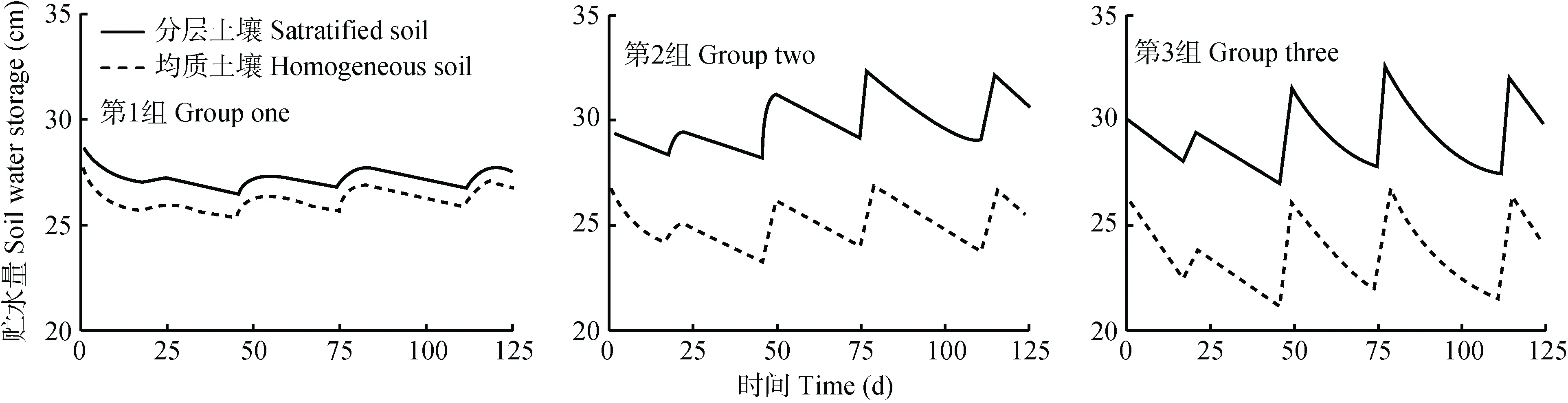
图8 3种饱和导水率组合下层状土壤(实线)和均匀土壤(虚线)储水量随时间的变化Fig. 8 Water storage of stratified soil (solid lines) and homogeneous soil (dashed lines) under 3 hydraulic conductivity combinations

图9 土壤水力参数饱和导水率(Ks)、饱和含水量(θs)、残余含水率(θr)、孔隙大小分布参数(α)和形状参数(n)增加或减少10%下土壤渗透量相对误差随时间的变化Fig. 9 Change of relative error of water seepage over time under 10% increase and 10% decrease of soil hydraulic parameters saturated water conductivity (Ks), saturated water content (θs), residual water content (θr), soil pore size parameter (α) and shape parameter (n)

从图 9可以看出, 相对于原始层状土壤和均匀土壤的渗透量相对误差, 增减 10%的层状土壤和均匀土壤的渗透率相对误差均发生了不同程度的变化。饱和导水率(Ks)增加10%, 相对误差减小幅度较大, 表明均匀土壤的渗透量比层状土壤的渗透量变小, 而Ks减少10%, 相对误差变化不大。这说明Ks增加比Ks减少对垂向均匀处理的影响更大。饱和含水量(θs)增加 10%, 相对误差增加幅度较大, 表明均匀土壤的渗透量比层状土壤的渗透量变大, 而θs减少 10%, 相对误差减小幅度较大, 表明均匀土壤的渗透量比层状土壤的渗透量变小。这说明θs增加和减少对垂向均匀处理的影响都较大。残余含水率(θr)增加和减小10%, 在50 h之后相对误差减小幅度较大, 表明均匀土壤的渗透量比层状土壤的渗透量变小。这说明θr增加和减少对垂向均匀处理有一定的影响。孔隙大小分布参数(α)增加 10%, 相对误差几乎不变, 而α减少10%, 相对误差先增大后减小, 表明均匀土壤的渗透量比层状土壤的渗透量先变大后变小。这说明α减少对垂向均匀处理的影响较大。形状参数(n)增加 10%, 相对误差减少幅度较大, 表明均匀土壤的渗透量比层状土壤的渗透量变小, 而n减少10%, 相对误差先增加后减少, 幅度变化较大,表明均匀土壤的渗透量比层状土壤的渗透量先变大后变小。这说明n增加和减少对垂向均匀处理的影响都较大。综合考虑这5个参数在增减10%之后对相对误差的影响, 排序是:n＞θs＞α＞Ks＞θr。说明形状参数n对渗透量的敏感性最强。

从图10可以看出, 相对于原始层状土壤和均匀土壤的储水量相对误差, 增减 10%的层状土壤和均匀土壤的储水量相对误差均发生了不同程度的变化。饱和导水率(Ks)增加10%, 相对误差减小幅度较大, 表明均匀土壤的储水量比层状土壤的储水量变小, 而Ks减少 10%, 相对误差增加幅度较大, 表明均匀土壤的储水量比层状土壤的储水量变大。这说明Ks增加和Ks减少对垂向均匀处理都有较大的影响。饱和含水量(θs)增加和减小10%, 相对误差增加幅度都较大, 表明均匀土壤的储水量比层状土壤的储水量变大。这说明θs增加和减少对垂向均匀处理的影响都较大。残余含水率(θr)增加10%, 相对误差几乎不变, 而θr减小 10%, 相对误差增加幅度较大,表明均匀土壤的储水量比层状土壤的储水量变大。这说明θr减少对垂向均匀处理有较大的影响。孔隙大小分布参数(α)增加和减小 10%, 相对误差增加幅度非常大, 表明均匀土壤的储水量比层状土壤的储水量要大很多。这说明α增加和减少对垂向均匀处理的影响都较大。形状参数(n)增加和减小 10%, 相对误差增加幅度都较大, 表明均匀土壤的储水量比层状土壤的储水量变大, 这说明n增加和减少对垂向均匀处理的影响都较大。综合考虑这 5个参数在增减10%之后对相对误差的影响, 排序是:α＞n＞Ks＞θs＞θr。说明土壤孔隙大小分布参数α对储水量的敏感性最强, 形状参数n其次。

图10 土壤水力参数饱和导水率(Ks)、饱和含水量(θs)、残余含水率(θr)、孔隙大小分布参数(α)和形状参数(n)增加或减少10%下土壤储水量相对误差随时间的变化Fig. 10 Change of relative error of water storage over time under 10% increase and 10% decrease of soil hydraulic parameters saturated water conductivity (Ks), saturated water content (θs), residual water content (θr), soil pore size parameter (α) and shape parameter (n)

3 结论

为了研究土壤垂向分层和均匀处理下的水分差异, 本文通过建立一维土壤水分运动模型, 并设置数值试验方案, 分析了 3组层状土壤和均匀土壤的水分分布、渗透量和储水量的差异, 并进一步分析了土壤水力参数包括饱和导水率Ks、饱和含水量θs、残余含水量θr、孔隙大小分布参数α和形状参数n这 5个参数对土壤垂向分层和均匀处理下水分差异的影响。通过上述研究, 得到如下结论:

1)本文建立的一维土壤水分运动模型模拟的土壤水分剖面与Yeh解析解和室内五水转化试验的土壤水分剖面一致, 表明模型无论是考虑还是不考虑根系吸水都具有可靠性。

2)对于上下层饱和导水率相差越大的层状土壤,采用垂向均匀方式处理, 会导致各个水文变量的差异变大。当层状土壤上下层饱和导水率相差1.5倍时, 层状土壤和均匀土壤水分分布的差别小于0.05 cm3·cm-3;而当层状土壤上下层饱和导水率相差达 3.3倍时, 层状土壤和均匀土壤的水分分布差别达 0.15 cm3·cm-3,渗漏量相差20 cm以上, 储水量相差5 cm左右。

3)相对于层状土壤下层, 均匀土壤下层的持水能力能差, 水流速度变快, 导致下层水分分布减小,渗漏量增加, 储水量减小。

4)形状参数n对渗透量的敏感性最强, 土壤孔隙大小分布参数α对储水量的敏感性最强, 形状参数n其次。

在实际应用中, 如果一个区域的土壤上下层饱和导水率相差较大, 那么垂向均匀处理可能会导致很大的误差, 和实际层状土壤的水分分布相差很大,这会严重影响土壤水分的准确估计, 在实际处理中需要认真考虑。

参考文献 References

[1] KOSTER R D, DIRMEYER P A, GUO Z C, et al. Regions of strong coupling between soil moisture and precipitation[J].Science, 2004, 305(5687): 1138–1140

[2] MAHMOOD R, HUBBARD K G. Simulating sensitivity of soil moisture and evapotranspiration under heterogeneous soils and land uses[J]. Journal of Hydrology, 2003, 280(1/4):72–90

[3] 李倩, 孙菽芬. 陆面过程模型中垂直非均匀土壤的水分传输及相变的模拟[J]. 大气科学, 2015, 39(4): 827–838 LI Q, SUN S F. The simulation of soil water flow and phase change in vertically inhomogeneous soil in land surface models[J]. Chinese Journal of Atmospheric Sciences, 2015, 39(4):827–838

[4] 雷志栋, 杨诗秀, 谢森传. 土壤水动力学[M]. 北京: 清华大学出版社, 1988 LEI Z D, YANG S X, XIE S C. Soil Hydrodynamics[M].Beijing: Tsinghua University Press, 1988

[5] MOLZ F J. Water transport in the soil-root system: Transient analysis[J]. Water Resources Research, 1976, 12(4):805–808

[6] SZYMKIEWICZ A, HELMIG R. Comparison of conductivity averaging methods for one-dimensional unsaturated flow in layered soils[J]. Advances in Water Resources, 2011, 34(8): 1012–1025

[7] 周维博. 降雨入渗和蒸发条件下野外层状土壤水分运动的数值模拟[J]. 水利学报, 1991, (9): 32–36 ZHOU W B. Numerical simulation of soil water movement in the field under rainfall infiltration and evaporation[J]. Journal of Hydraulic Engineering, 1991, (9): 32–36

[8] VAN DAM J C, GROENENDIJK P, HENDRIKS R F A, et al.Advances of modeling water flow in variably saturated soils with SWAP[J]. Vadose Zone Journal, 2008, 7(2): 640–653

[9] SRIVASTAVA R, YEH T C J. Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils[J]. Water Resources Research, 1991, 27(5): 753–762

[10] 谭丽萍. 主要生态与水文过程及其对变化响应的VIP模拟、实验验证与预测[D]. 北京: 中国科学院大学, 2016 TAN L P. VIP simulation, experimental verification and prediction of the main ecological and hydrological processes and their response to change[D]. Beijing: University of Chinese Academy of Sciences, 2016

[11] VOGEL T, CISLEROVA M. On the reliability of unsaturated hydraulic conductivity calculated from the moisture retention curve[J]. Transport in Porous Media, 1988, 3(1): 1–15

[12] VOGEL T, VAN GENUCHTEN M T, CISLEROVA M. Effect of the shape of the soil hydraulic functions near saturation on variably-saturated flow predictions[J]. Advances in Water Resources, 2000, 24(2): 133–144

[13] 赵晶晶. 作物生长条件下土壤水分运动数值模拟[D]. 乌鲁木齐: 新疆农业大学, 2007 ZHAO J J. The numerical modeling for soil water movement under the condition of planting of crop[D]. Urumchi: Xinjiang Agricultural University, 2007

[14] 刘苏峡, 毛留喜, 莫兴国, 等. 黄河沿岸陕豫区土壤水分的空间变化特征及其驱动力因子分析[J]. 气候与环境研究,2008, 13(5): 645–657 LIU S X, MAO L X, MO X G, et al. Analysis of spatial variability of soil moisture and its driving force factors in the Shaanxi-Henan Region along the Yellow River[J]. Climatic and Environmental Research, 2008, 13(5): 645–657