Stability Analysis of Network Controlled Temperature Control System with Additive Delays

V. Venkatachalam and D. Prabhakaran

1 Introduction

In this paper, stability of network controlled heat exchanger system, also known as temperature control system that maintains output temperature of a fluid within specified limits is analyzed. When heat exchanger is employed for transfer of heat between one or more fluids, closed loop control is very essential and stability of the closed loop system is significant. The fluids in a typical heat exchanger system may be separated by a solid wall to prevent mixing or they may be in direct contact also [Kakac and Liu (2002);Saunders (1988)]. The heat exchangers are widely used in space heating, refrigeration, air conditioning, power generations, chemical industries, petrochemical and petroleum industries, Oil-industries, gas-industries and sewage treatment [Kakac and Liu (2002);Saunders (1988); Stephanopoulas (2003)]. If the heat exchanger system is controlled through a master control center located at remote, then the feedback loop of the closedloop control scheme will be completed through communication networks. Such a typical network controlled temperature control scheme will consist of heat exchanger, sensor,valve, and a regulator (embedding PI control logic) placed at the remote control center[Sharma, Gupta and Kumar (2011)]. The temperature control scheme will be pressed into service in the event of any unexpected deviation in the temperature control system output variable like sudden excessive withdrawal of steam by output loads. Under such perturbed operating condition, the temperature sensor sense the output temperature. This signal is feedback to the controller unit through a communication network (as digitally processed data packets). In the controller, the error between the reference signal and actual signal (delayed by communication network) is computed and processed by proportional-integral (PI) control scheme. The PI controller subsequently offers a suitable input signal through the communication network to the final control element (the valve)thereby bringing the perturbed heat exchanger terminal temperature back to the equilibrium condition. The heart of the heat exchanger control scheme, the PI controller,is designed apriori assuming zero network delays. However, the use of communication network for data (signal) transfer in the closed-loop system introduces time-delays in the feedback path. This, in turn, will enable one to achieve optimal performance from the time-delayed system [Batisha and Jota (2014)]. Delay dependent stability criteria are employed to compute the stable margin for the network delays within which the temperature control system remains asymptotically stable. To the best of author’s knowledge, the delay-dependent stability of heat exchanger [Yeroglu (2015)]. These two feedback-loop delays, popularly referred to as network induced delays, are practically unavoidable in a distributed control system scenario where the plant and controller are connected through a communication channel in which the data (control or/and measured)experience buffering, processing and propagation at various internodes; refer Zhao et al.[Zhao, Liu and Rees (2010)]. As a result, the network-introduced two additive delays are time-varying in nature and have dissimilar characteristics [Lam, Goa and Wang (2007)].In general case, these network induced delays are inevitably pose serious limitations to achievable performance of the closed loop system, and in some cases, may even lead to destabilization of the temperature control system. Hence, stable delay margin (i.e.maximum delay bound which the networked controlled system can accommodate without losing asymptotic stability) for such temperature control system must be computed for various subsets of controller parameters (proportional gain Kpand integral gain KI)through delay-dependent stability analysis procedure so that they serve as a practical guide-line for fine tuning of controller parameters at the implementation stage. System under networked control environment has not been reported in literature so far. In this paper, a generalized criterion (sufficient condition) is presented for ascertaining delay dependent stability of temperature control systems with time-varying additive feedback loop delays.

In the proposed approach, the mathematical model of the PI controlled temperature control system with time-varying feedback loop delays is first developed as a linear retarded delay-differential continuous-time equation. This state-space model is a generalized modelling framework for dynamical systems with time-delays. Subsequently,based on Lyapunov-Krasovskii functional approach combined with Reciprocal convex combination [Ko and Park (2011)], a delay-dependent stability criterion is presented in LMI framework to compute the maximum value bound of the time-delay within which the closed-loop heat exchanger (temperature control) system remains asymptotically stable in the sense of Lyapunov. The paper concludes with the presentation of simulation results of substantiate the analytical results on delay-dependent stability. The proposed stability criterion is expressed as a set of solvable linear matrix inequalities (LMIs) that can be solved using standard numerical packages [Gahinet, Nemirovskii, Laub et al.(1995)] by casting it as a convex optimization problem.

These adequate conditions generally indicated as stability criteria are expressed as a set of solvable LMI conditions [Xu and Lam (2008)]. The less conservatism of new delaydependent stability criteria mainly depends on the selection of the LK functional used in the analysis, and many useful results have been reported in literature in recent times [Lam,Goa and Wang (2007); Xu and Lam (2008); Gao, Chng and Lam (2008); Wu, Liao, Feng et al. (2009); Ramakrishnan and Ray (2009, 2011b); Dey, Ray, Ghosh et al. (2010); Shao and Han (2012); Shao, Zhu, Zhang et al. (2013); Li and Tian (2012); Ko, Lee and Park(2011); Jiao (2013); Chaibi, Tisser and Hmamed (2013); Hamed, Chaabane and Kacem(2011)]. However, many useful results existing in the literature, to the best of our knowledge, there are no results available for the delay-dependent stability of temperature control system with additive time-varying delays.

2 Temperature control model with additive time-varying delays

The linear model of temperature control system is used to analyze the system dynamics and to design a controller [Sharma, Gupta and Kumar (2011)]. Fig. 1 shows the block diagram of a temperature control with including network-induced time-delays. Now that each component of the system namely heat exchanger, sensor, valve, the controller is modeled by a first-order transfer function [Sharma, Gupta and Kumar (2011)]. They repeated here for convenience:

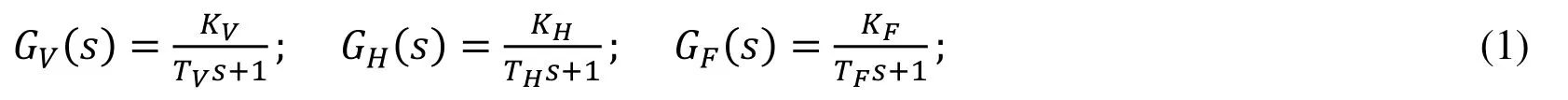
where KV,KHand KFare the gains of a valve, heat exchanger and sensor respectively, and TV,THand TFare the corresponding time constants. The transfer function of the PI controller is given below:

where KPand KIare the PI controller gains respectively; the proportional term controls the rate of temperature rise after initial transients. The integral controller gain adds a pole at the origin and increases the system type by one and hence reduces the steady-state error[Ramakrishnan and Ray (2016)]. The combined effect of the PI controller gains will structure the response of the temperature control system with reduced overshoot and faster settling time.

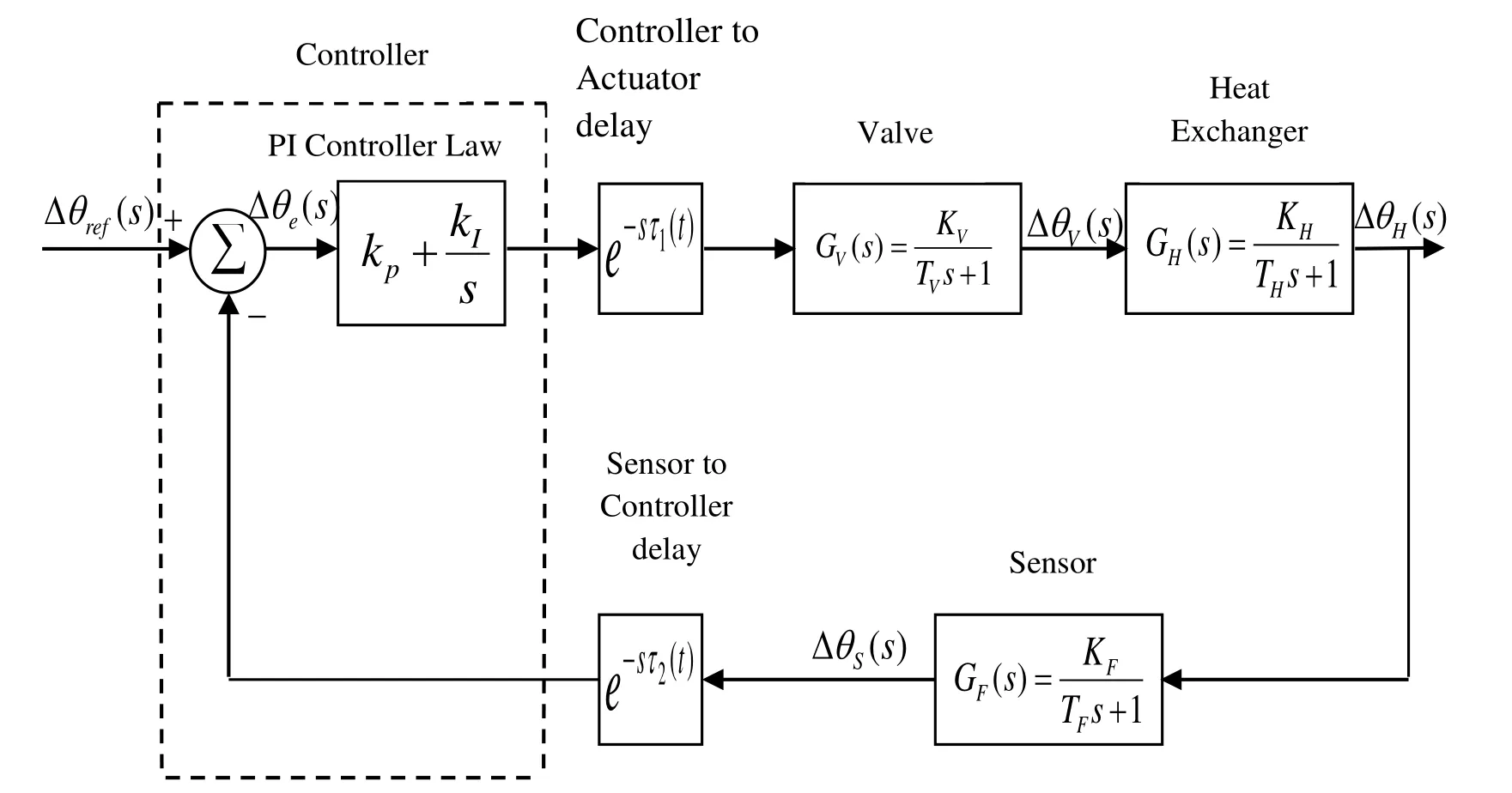
Figure 1: Block diagram of closed loop temperature control system with additive timevarying delays

In the Fig. 1 τ1(t) portrays sensor to controller delay (measuring delay) and τ2(t)portrays controller to actuator delay (processing delay).

3 System description and problem statement

The general state-space model of the additive state-delayed system is given by:

where x(t)∈ ℝn×1is the state vector, A ∈ ℝn×nare system matrices, ∅(t) is the initial condition of the system for,

Consider the system (3) with the following system matrices are:

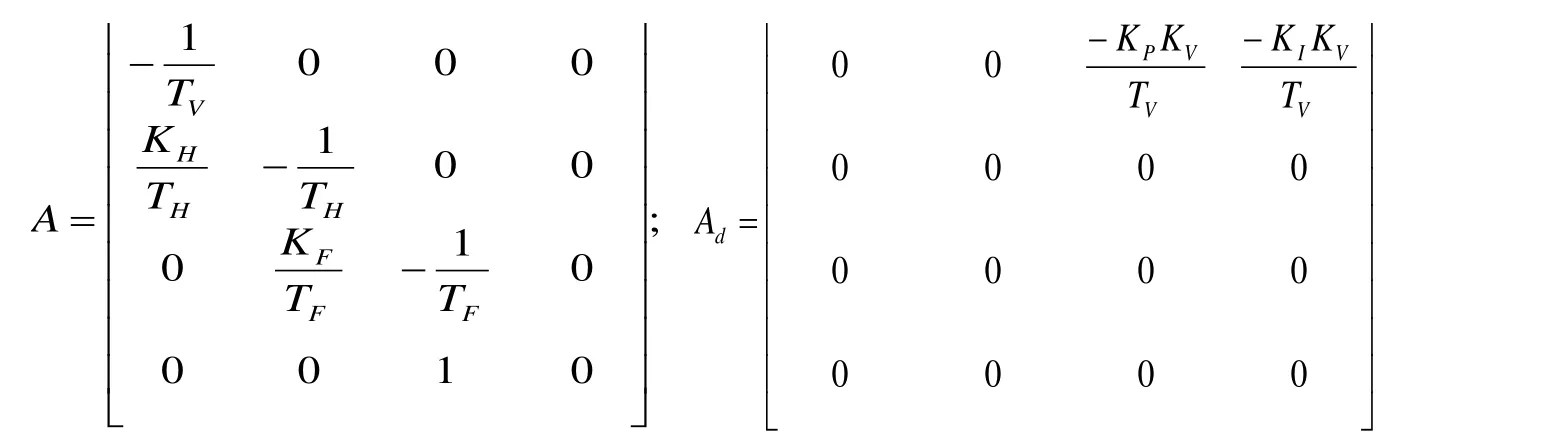
The time-varying additive delays τ1(t) and τ2(t) are satisfying the following conditions:

Lemma 1 [Zhu and Yang (2008)]: For any positive symmetric constant matrix N ∈ ℝn×n,scalars η1and η2satisfying η1＜ η2, a vector valued function ω:[η1, η2]→ ℝnsuch that the integration concerned are well defined, then following inequality holds:

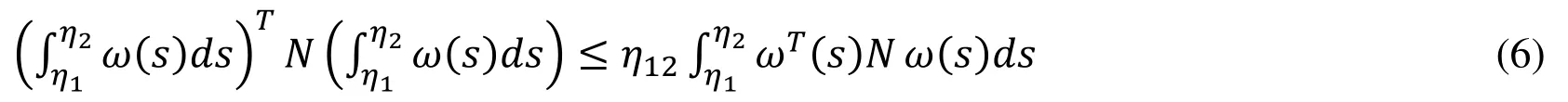
where

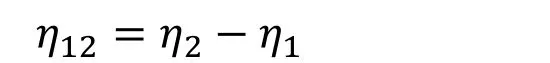
Lemma 2: For a continuous function f(x) and its derivative f′(x) are defined on [a,b],then

Lemma 3 [Ko and Park (2011)]: For any vectors ε1,ε2, matrices P ＞ 0,Q and real numbers α1＞ 0,α2＞ 0 with α1+ α2=1 satisfying

The following inequality condition holds:

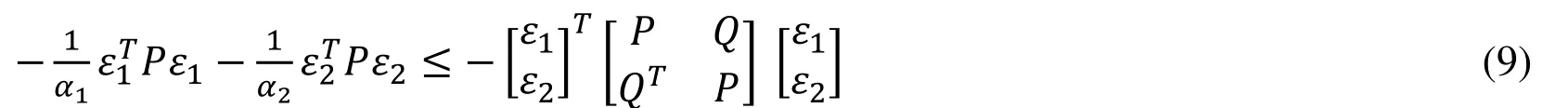
Proof: The condition (8) implies that

which gives

By using the relationship α1+ α2=1 on (11) and by rearranging the terms, we deduce the inequality condition (9).

4 Main results

In this section, the new stability criterion for the temperature control system with additive time-varying delay is presented in the following theorem.

Theorem: Given non-negative scalarsthe system (1) satisfying the conditions (4) and (5) is asymptotically stable, if there exists real, positive, symmetric matrices Z,R,Qi,i=1,2,3 ; free matrices S12,S13,S23of appropriate dimensions such that following LMI conditions hold:

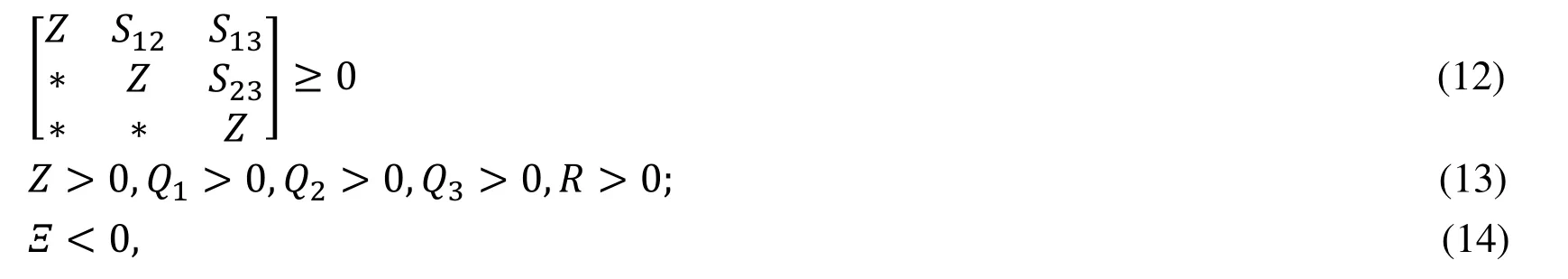
where

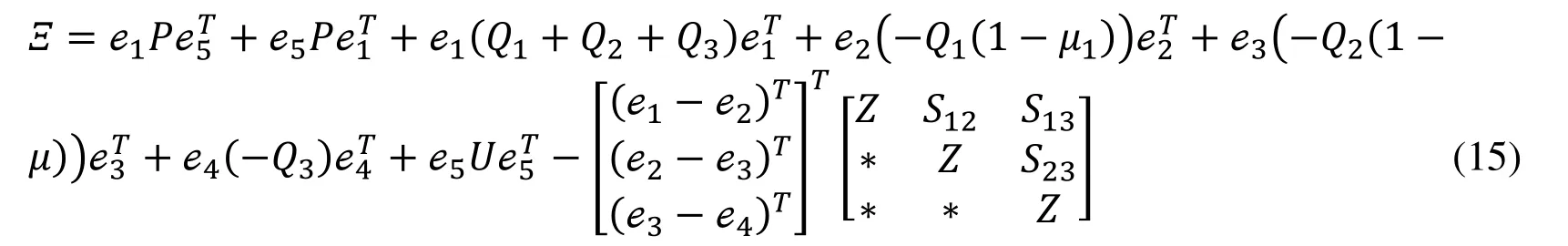
with

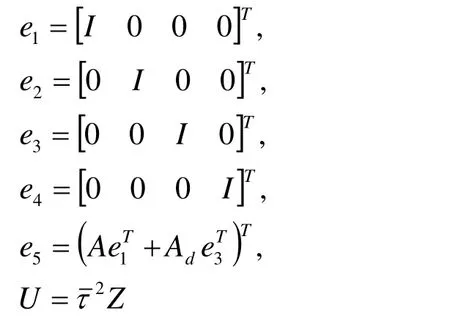
where

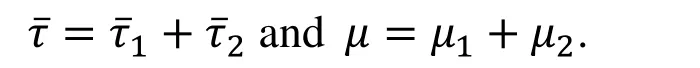
Proof: consider the LK functionalwith

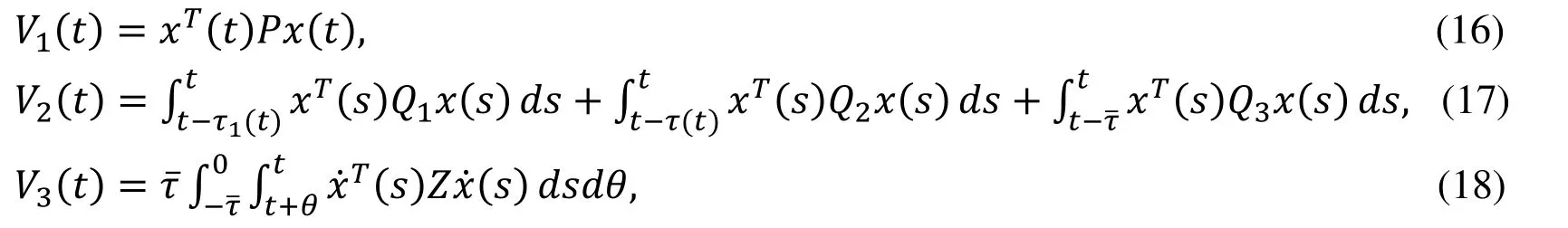
where P,Qi,i=1,2,3, and Z are real symmetric positive definite matrices, and τ(t)=Define

The time-derivative of the functional Vi(t),i=1,2,3, is computed along the trajectory of(3) as follows: The time-derivative of1(t) is given by

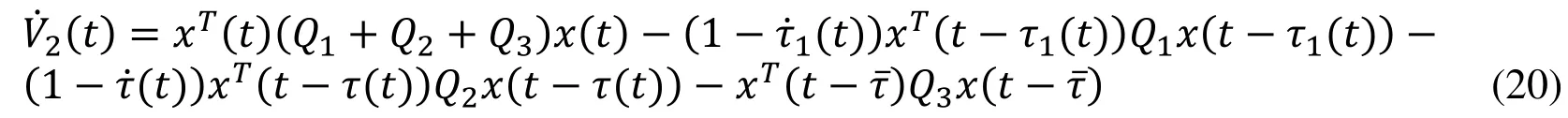
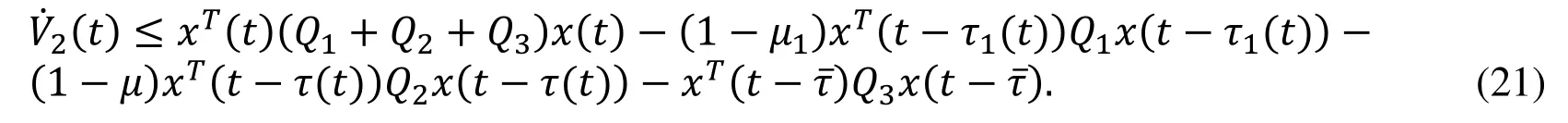
In other words, Eq. (21) can be revealed in terms of η(t) as follows:

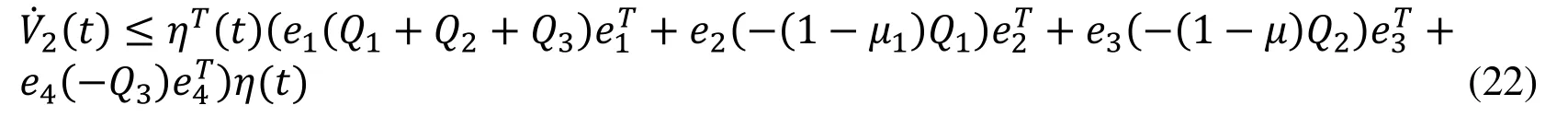
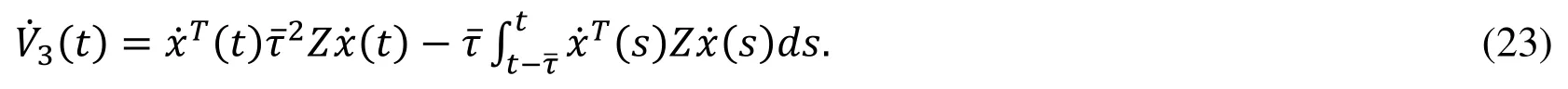
The Eq. (23) can be rewritten by expanding the integral part as follows:

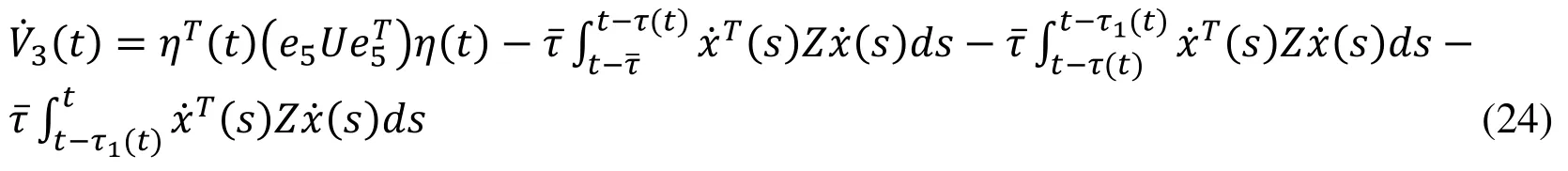
Which, for applying Lemma 1, is rewritten on Eq. (24), we get

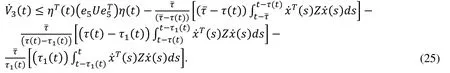
Now, by applying Lemma 1 on Eq. (25), we get

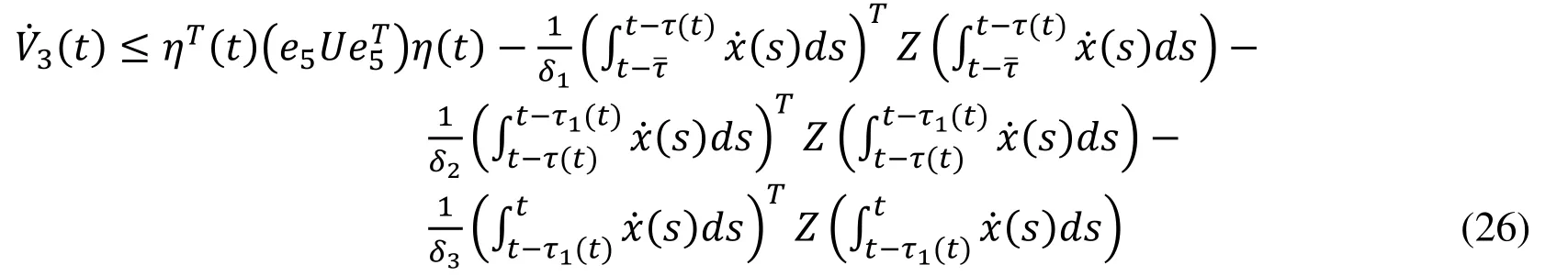
Now, we can express Eq. (26) as follows:

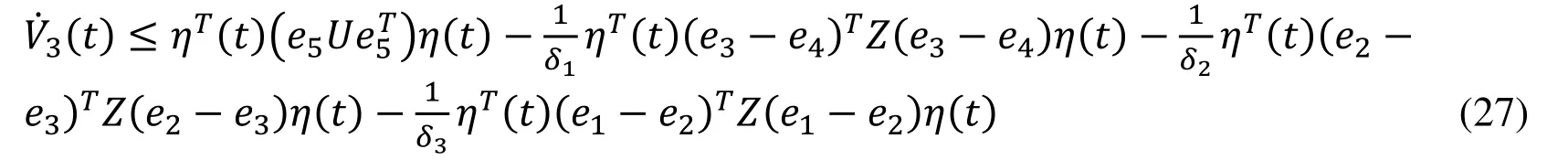
Since δ1+ δ2+ δ3=1,∀t, the reciprocal convex combination technique of Eq. (27) is dealt using Lemma 3 as follows:

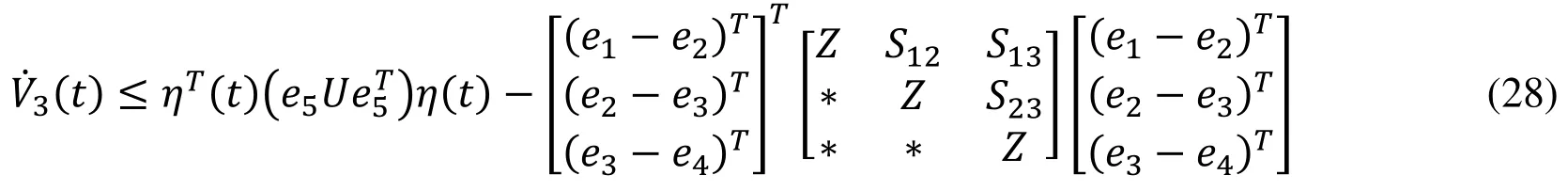
Provided

holds with S12,S13and S23being free matrices of any dimensions.

If the condition Ξ＜0 and relation (29) holds simultaneously, which the additive timedelay system (3) with satisfying the condition (4) and (5) is asymptotically stable.

5 Results and discussions

In this discussion, the effectiveness of the stability criterion is presented for temperature control system with additive time-varying delays is illustrated. The maximum allowable delay margin for additive time-varying delaysandfor stability for a pick range of PI controller gains is computed. The gains and time constants of the temperature control used in the analysis are as follows [Ko and Park (2011)].

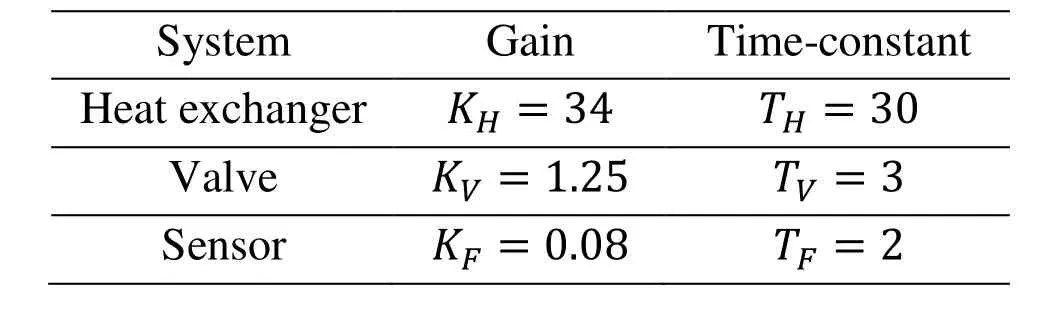
Table 1: Parameter values of temperature control system

For the aforesaid system parameters with delay free condition, the controller capability curve can be obtained easily; it is illustrated in Fig. 2. From the Fig. 2, it is clear that for all values of KPand KIlying below the controller capability curve, the closed-loop system is asymptotically stable. From the curve we choose KP=2 and KI=0.15s−1,then the closed loop system converges asymptotically to equilibrium point as illustrated in Fig. 3 for a unit step perturbation in temperature control system output variable (from its equilibrium value).

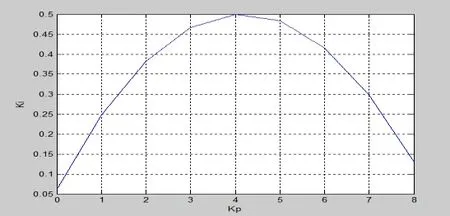
Figure 2: Maximum value of KI for different values of KP

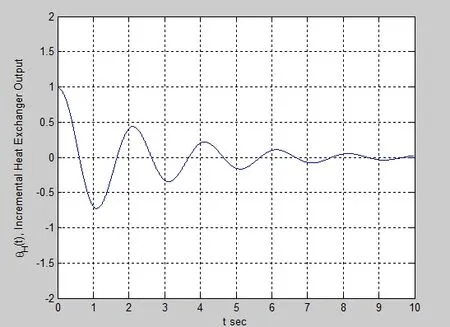
Figure 3: Evolution of ∆θH(t) less than zero delay condition

when the network delay τ is made zero, the system Eq. (3) becomes

Now, it is observed that the Eigenvalues of the system state matrix and input matrix(A+Ad) depend on the controller parameters KPand KI. Tab. 2 given the maximum values of KI(s−1) for a fixed value of KPfor which the temperature control system is on the verge of instability i.e. having one complex conjugate pair of eigenvalues on the jω axis. It is observed from the Fig. 3 that there is a tendency for the curve to decrease gradually with the increase of KI.

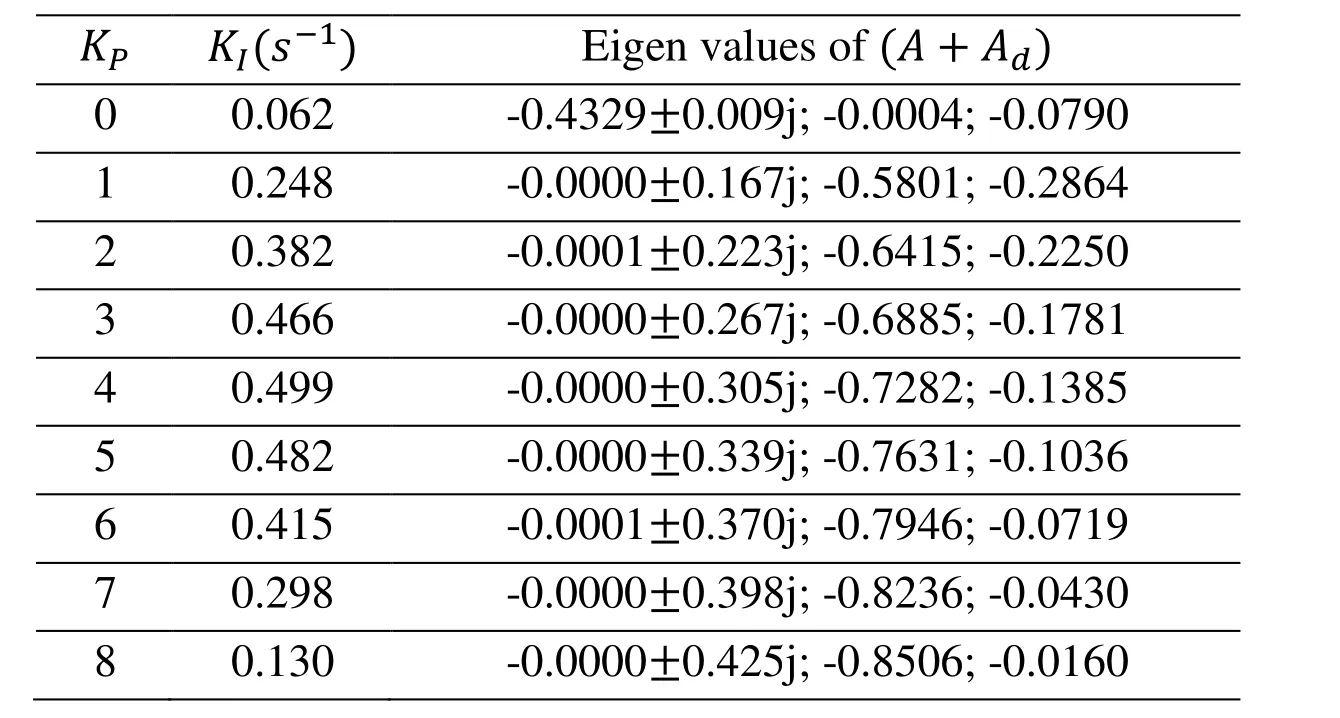
Table 2: Maximum integral controller gain for a given KP

Now, when this PI controller operates atop a networked environment, the temperature control system will be subjected to additive network induced time-varying delays τ1(t)and τ2(t). Let the time-derivative of the additive time-varying delays be bounded asand. Let choose the controller parameter KP=2 and KI=0.15s−1, in the presence of network induced delays, according to the stability criterion are presented in theorem, the temperature control system is stable up to τ1=1 second τ2=1.3305 seconds, and if network induced delays is increased far beyond this value,the system output becomes unbounded evolution. Hence, this analysis clearly brings to the impact of the network induced delays on stability and performance of the system. Let μ1=0.1, and μ2=0.2. for different values of KPand KI, from the capability curve, the maximum allowable delay boundfor a givenis given in Tabs. 3-7. Likewise, Tabs.8-12 give the maximum allowable delay boundfor a given. From the tables, it is clear that as the various values of KPand KI, the maximum delay bound that system can accommodate without losing stability decreases. The corresponding stability margin presented in Fig. 4 clearly indicates lessening.

Table 3: Maximum allowable delay bound for a given

Table 3: Maximum allowable delay bound for a given

Table 4: Maximum allowable delay bound for a given

Table 4: Maximum allowable delay bound for a given

Table 5: Maximum allowable delay bound for a given

Table 5: Maximum allowable delay bound for a given

Table 6: Maximum allowable delay bound for a given

Table 6: Maximum allowable delay bound for a given

Table 7: Maximum allowable delay bound for a given

Table 7: Maximum allowable delay bound for a given

Table 8: Maximum allowable delay bound for a given

Table 8: Maximum allowable delay bound for a given

Table 9: Maximum allowable delay boundfor a given

Table 9: Maximum allowable delay boundfor a given

Table 10: Maximum allowable delay bound for a given

Table 10: Maximum allowable delay bound for a given

Table 11: Maximum allowable delay boundfor a given

Table 11: Maximum allowable delay boundfor a given

Table 12: Maximum allowable delay bound for a given

Table 12: Maximum allowable delay bound for a given

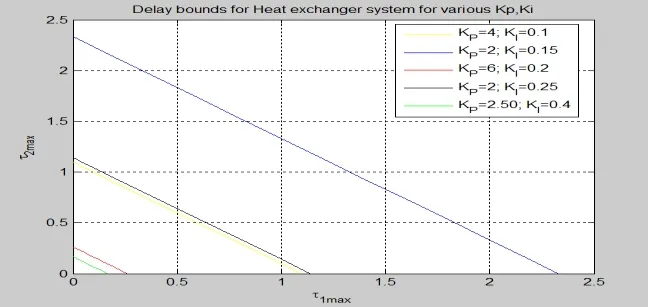
Figure 4: Stability margin for temperature control of heat exchanger

Simulation study of the closed-loop temperature control system was carried out for zero network delay is confined to the stable region shown in Fig. 3; it is easy to infer the influence of network delays on the stability of the system. As network delays increase,the response of the temperature control system gets malformed and for higher delays, the closed-loop system becomes unstable.

6 Conclusion

In this research, the problem of delay-dependent stability of temperature control systems with additive time-varying delay has been addressed using Lyapunov-Krasovskii functional technique. In the stability analysis, the temperature control system is mathematically modeled in terms of state space model, and reciprocal convex combination technique is employed in the stability analysis to make it less number of decision variables. The proposed results are validated benchmark temperature control system with time-varying additive delays. The deduced results of this paper impart more realistic operating condition in a real-time temperature control system.

Acknowledgement:One of the authors (Dr. D. Prabhakaran) is grateful to All India Council for Technical Education (AICTE), New Delhi, India for financial support (File No.20/AICTE/RFD/RPS (Policy-II) 23/2013-16). The authors would like to express their sincere thanks to Dr. S. R. K. Prasad (Correspondent, CIT), Dr. R. Prabhakar (Secretary, CIT), Dr. V.Selladurai (Principal, CIT), Dr. M. Thirumarimugan (Head of the Department of Chemical Engineering, CIT) for their useful discussions and encouragement during the course of work.Also, we like to acknowledgment Dr. T. Venkatachalam (Associate Professor of Physics,Coimbatore Institute of Technology, Coimbatore, India) for their valuable help in studying dynamical system with time delays.

Batisha, A. P.; Jota, F. G.(2014): Effects of time delay statistical parameters on the most likely regions of stability in an NCS. Control Engineering and Applied Informatics,vol. 16, pp. 3-11.

Chaibi, N.; Tisser, E. H.; Hmamed, A.(2013): Delay-dependent robust stability of singular systems with additive time-varying delays. International Journal of Automation and Computing, vol. 10, no. 1, pp. 65-90.

Dey, R.; Ray, G.; Ghosh, S.; Rakshit, A.(2010): Stability analysis for continuous system with additive time-varying delays: a less conservative result. Applied Mathematics and Computation, vol. 215, no. 10, pp. 3740-3745.

Gahinet, P.; Nemirovskii, A.; Laub, A. J.; Chilali, M.(1995): Control toolbox for use with Matlab. Mathworks, Natick.

Gao, H.; Chng, T.; Lam, J.(2008): A new delay system approach to network-based control. Automatica, vol. 44, no. 1, pp. 39-52.

Hamed, B. B.; Chaabane, M.; Kacem, W.(2011): Absolute stability of nonlinear systems with two additive time-varying delay components. International Journal of Automation and Computing, vol. 10, no. 1, pp. 39-45.

Jiao, J. M.(2013): A stability criterion for singular systems with two additive timevarying delay components. International Journal of Automatica, vol. 10, no. 1, pp. 39-45.

Kakac, S.; Liu, H.(2002): Heat exchangers: selection, rating and thermal design (2nd edition). CRC Press.

Ko, J. W.; Lee, W. I.; Park, P. G.(2011): Delayed system approach to the stability of networked control systems. International Multi conference of Engineers and Computer Scientists, vol. 2, pp. 16-18.

Ko, J. W.; Park, P. G.(2011): Reciprocally convex approach for the stability of networked control systems. Intelligent Control and Innovative Computing, vol. 110, pp. 1-9.

Lam, J.; Goa, H.; Wang, C.(2007): Stability analysis for continuous systems with two additive time-varying delay components. System and Control Letters, vol. 56, no. 1, pp. 16-24.

Li, T.; Tian, J.(2012): Convex polyhedron method to stability of continuous systems with two additive time-varying delay components. Journal of Applied Mathematics.

Ramakrishnan, K.; Ray, G.(2009): Delay-dependent stability analysis of linear systems with additive time-varying delays. 5th Annual IEEE Conference on Automation Science and Engineering, Bangalore, India, pp. 122-126.

Ramakrishnan, K.; Ray, G.(2011b): Stability criteria with less LMI variables for linear system with additive time-delays. Journal of Applied Mathematics and Computing, vol.36, no. 1-2, pp. 263-274.

Ramakrishnan, K.; Ray, G.(2016): Stability criterion for networked control systems with additive time-varying state-delays and bounded nonlinearity. International Journal of Systems,Control and Communications, vol. 7, no. 1, pp. 68-82.

Saunders, E. A.(1988): Heat exchanges: selection, design and construction. Longman Scientific and Technical, New York.

Shao, H.; Han, Q. L.(2012): On stabilization for systems with two additive time-varying input delays arising from networked control systems. Journal of the Franklin Institute,vol. 349, no. 6, pp. 2033-2046.

Shao, H.; Zhu, X.; Zhang, Z.; Zhong, G.(2013): Delay-dependent H∞ control for systems with two additive time-vary delays. Journal of Control Engineering and Technology, vol. 3, no. 2, pp. 90-97.

Sharma, C.; Gupta, S.; Kumar, V.(2011): Modeling and simulation of heat exchanger used in soda recovery. Proceedings of the World Congress on Engineering, vol. 2.

Stephanopoulas, G.(2003): Chemical process control. Prentice-Hall of India Private Limited, pp. 209-211.

Wu, H.; Liao, X.; Feng, W.; Guo, S.; Zhang, W.(2009): Robust stability analysis of uncertain systems with two additive time-varying delay components. Applied Mathematical Modelling, vol. 33, no. 12, pp. 4345-4353.

Xu, S.; Lam, J.(2008): A survey of linear matrix inequality techniques in stability analysis of delay systems. International Journal of Systems Science, vol. 39, no. 12, pp. 1095-1113.

Yeroglu, C.(2015): Robust stabilizing PID controllers for multiple time delay systems with parametric uncertainty. Control Engineering and Applied Informatics, vol. 17, pp. 20-29.

Zhao, Y.; Liu, G.; Rees, D.(2010): Packet-based dead-band control for internet-based networked control system. IEEE Transactions on Control Systems Technology, vol. 18,no. 5, pp. 1057-1067.

Zhu, X. L.; Yang, G. H.(2008): Jensen integral inequality approach to stability analysis of continuous-time systems with time-varying delay. IET Control Theory and Applications, vol.2, no. 6, pp. 524-534.