AdaBoosting Neural Network for Short-Term Wind Speed Forecasting Based on Seasonal Characteristics Analysis and Lag Space Estimation

Haijian Shao and Xing Deng,

1 Introduction

Wind energy, as a typical renewable, inexhaustible and free energy resource, has been considered as an optimal solution to solve the problems caused by the traditional energy[Wang, Song, Liu et al. (2016)]. Wind energy production requires accurate and reliable wind power forecasting which in turn is closely related to wind speed forecasting. Up to date, precise short-term wind speed forecasting unfortunately remains a challenging issue due to wind’s randomness and intermittent nature [Shao, Wei, Deng et al. (2016)].Usually, randomness and nonstationary can cause the portion problem of the wind speed forecasting [Grilli and Shumchenia (2015)].

(1) In the literature, numerical weather prediction [Abd-Elaal, Mills and Ma (2018)]hydrological evaluation methods [Honti, Scheidegger and Stamm (2014)], probabilistic model [Dowell and Pinson (2016)] and neural network (NN) [Chang, Lu, Chang et al.(2017)], etc. have all been considered to analyze the uncertainty effects in climate change and wind power penetration. Du et al. [Du, Wang, Wang et al. (2016)] discussed the significant characteristics of the randomness in wind power system output, and figured out that the potential influence factors which can influence the power capacity credit on different output levels. Roy [Roy (2013)] gave a comprehensively and quantitatively description for the randomness of wind speed to evaluate the outputs variability. In order to reduce the potential influence on power system operation from the randomness of the wind speed, Ding et al. [Ding, Hu and Song (2012)] utilized the stochastic optimization method to optimize the gird plant scheduling. Wavelet analysis as a powerful time-frequency analysis method can capture the local feature of the any time series are widely used in short-term wind speed forecasting and used to reduce the negative influence caused by randomness.

(2) Aiming at the assessing the statistical characteristics and modeling the uplift capacity,Shademan et al. [Shademan, Barron, Balachandar et al. (2014)] utilized the numerical simulation of wind speed loading of the full panel to analyze the effects of the lateral gap spacing and seasonal distribution pattern. The experiments denoted that two bottom panels experience larger mean wind loading compared to the top panels. This benefits the analysis of the wind speed’s seasonal distribution pattern and model configuration.

Neural network with its strong nonlinear mapping modeling ability is currently the most widely used method in the short-term wind speed or wind power forecasting. Recently,many studies indicated that the analysis method in combined with NN can significantly improve the forecasting accuracy of the short-term wind speed. Kavousi-Fard et al.[Kavousi-Fard, Khosravi, Nahavandi et al. (2016)] proposed a fuzzy-based approach in combination with NN optimized by the lower upper bound estimation to capture the uncertainty of the wind power and improve the forecasting accuracy. Meng et al. [Meng,Ge, Yin et al. (2016)] used the wavelet packet decomposition, crisscross optimization algorithm and artificial NNs to develop a new hybrid approach for short-term wind speed forecasting. The forecasting result indicated that the NN in combined with WT etc has the minimum mean absolute percentage error regardless of one-step, three-step or five-step prediction. Analogy, Ren et al. [Ren, Suganthan, Srikanth et al. (2015)] used the empirical mode decomposition-based to capture the stationary feature of wind speed, and combined with NN to establish the short-term model with high forecasting accuracy.Theoretically, although the feedforward NN with a single hidden layer can approximate any complex function, only the proper model architecture is beneficial to the acquisition of forecasting model with high accuracy. Our previously work [Wei, Shao, Deng et al.(2015)] indicated that the proper model structure selection can eliminate the unreasonable trend of data as well as feature extraction without loss of data characteristics. In addition,the forecasting accuracy can be further improved based on two following issues:

(1) Persistence of excitation for modeling.The training samples need to contain the sufficient features that they can be used to help improve the accuracy of the forecasting model. More precisely, more data sets or larger training sample sizes may be not conducive to the establishment of high-precision model unless they have enough effective features for training.

(2) Model lag estimation.The curve-fitting degree and cut-off distribution are usually selected as the principle to evaluate the model order. Lipschitz condition, Akaike Information Criterion and Bayesian Akaike Information Criterion are the most widely used methods to evaluate the model order. However, its significant drawback is that the outlined criteria are independent with the forecasting modeling. Based on the previous discussion, two following strategies are given:

(1) Seasonal characteristics analysis for persistence of excitation.The inputs of the neural network must be continuously energized, i.e. the input variables must be able to fully energize all model’s modes. Periodicity detection based on WT is conducive to extract the repetitive, stable and periodic characteristics of the wind speed time series.This obviously benefits that the various modes of the NN are continuously energized, and the spectrum of the training sample contains the pre-established model’s spectrum;

(2) Lag space evaluation for model lag estimation.The nonlinear mapping between the input-output is helpful to reflect the logical relationship between the historical input data and the current output data, and it is helpful to establish the feedforward NN with high generalization ability. Lipschitz quotients as a powerful measure method are used to calculate the proper delay of the chosen model.

The rest of this paper is organized as follows. The proposed approach includes the seasonal characteristics analysis (SCA) and lag space estimation etc. is given in Section 2.In Section 3, experimental evaluation is given to verify the performance of the proposed approach, and this paper is concluded in Section 4.

2 Proposed approach

The main objective of this paper is to propose a robust forecasting model with high accuracy by properly analyzing seasonal characteristics and lag space in wind resource,etc. The processing steps in general are specified as follows:

Step 1: Detect the irrelevant data and noisy to improve the sample quality. The irrelevant data and noisy will be effectively detected based on the WT.

Step 2: WT is used to decompose the original signal, extract the stationary component and reflect the similar frequency feature with respect to wind speed.

Step 3: Satisfy the persistence of excitation for NN, and ensure that the training sample contains enough seasonal characteristics used for testing. The proper subsets division is generated based on the different seasonal characteristics.

Step 4: Lag space estimation and model robustness enhancement. Lipschitz quotient and AdaBoosting NN are used to reflect the appropriate model structure and enhance the model robustness, respectively.

Experimental evaluation based on the dataset from NREL in 2004 is given to evaluate the performance of the proposed approach. The processing flow of this paper is stated in Fig. 1.

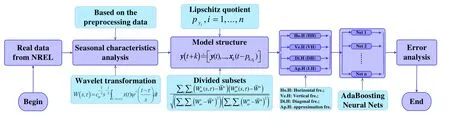
Figure 1: The processing flow

Firstly, WT is given to detect the wind variation pattern and capture the seasonal characteristics in different seasons. Secondly, wavelet decomposition is used to estimate the approximate frequency and extract the stationary component of wind speed to reduce the influence of the uncertainty in wind resources. Thirdly, Lipschitz quotient is used to estimate the lag space, reflect the model lag between the output power and the historical wind speed and power, and then promote the architecture configuration. Fourthly,AdaBoosting NN is utilized to promote the model configuration and enhance the model robustness. Finally, experimental comparison based on the dataset from NREL in 2004 is given to evaluate the performance of the proposed approach.

2.1 Seasonal characteristics analysis

WT composes of discrete and continuous wavelet transformation, which can be used to capture the distribution of the wind speed in different seasons based on the multi-frequency bands with multi-resolutions along with time. WT can detect the wind variation pattern and capture the seasonal feature in different seasons [Duo-Neng,Zhong-Xi, Zheng et al. (2016); Shao, Wei, Deng et al. (2016)]. Morlet function is dedicated to the meteorological time series analysis because its waveform shape is close to the analyzed signal [Megahed, Moussa, Elrefaie et al. (2008); Shao, Deng, Cui et al.(2016)]. The continuous wavelet transformation is defined by

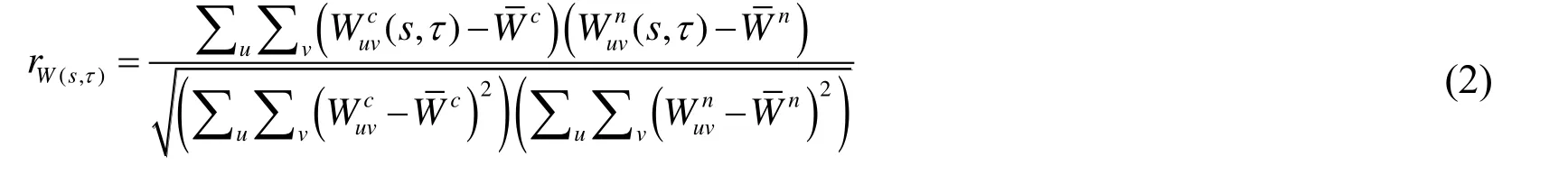
2.2 Randomness analysis and model lag estimation

Lipschitz quotient [He and Asada (1993)], wavelet decomposition and AdaBoost technique [Shao, Deng, Cui et al. (2016)] are used to estimate the model lags space,reduce the influence from the randomness and non-stationary. Model order is generally treated as the maximum lag to reflect the intrinsic relations between the output and the historical data. Lipschitz quotient is a powerful measure method with computational efficiency used to calculate the proper delay based on the chosen model, which is given by

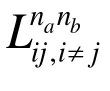
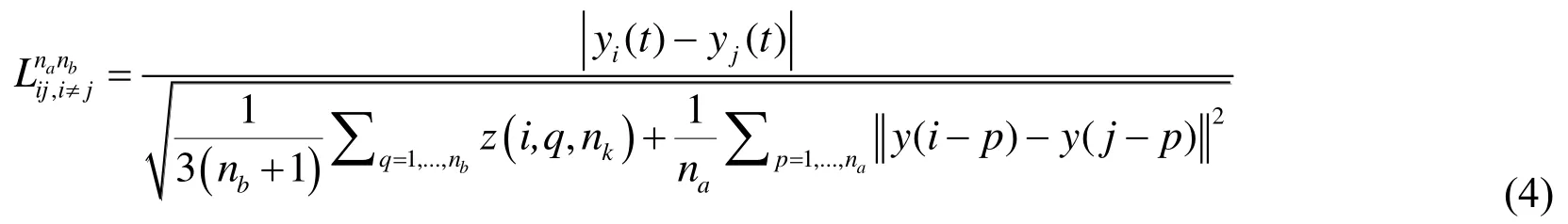
2.3 Model performance

The validation of the model results is used to evaluate the produced error in short-term wind speed forecasting. The proposed approach in this paper is mainly based on the multi-layered perceptron with one hidden layers NN using the Levenberg-Marquardt optimization method. Two performance criteria are used in this paper: Root mean square error (RMSE), Relative standard deviation (RSD), and they respectively defined by

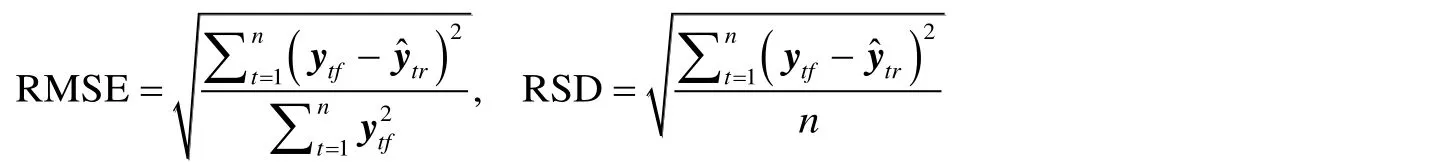
3 Experimental evaluation

3.1 Data description

The sample used for experimental evaluation is downloaded from the National Renewable Energy Laboratory (NREL) at: http://www.nrel.gov/electricity/transmission/.The sample contains two variables: wind speed (M/S) and netpower (MW). The site number of the utilized sample is 06996, and the sampling frequency is 10 min/point. In order to effectively reflect the seasonal characteristics of wind speed trend in a whole year, the sample size is 26352×1 (only the wind speed) from January 1, 2004 to December 31, 2004 is selected for analysis. In this section, the verification steps corresponding to the proposed approach are given in detail:

Step 1: Detect the irrelevant data and noisy to improve the sample quality. The irrelevant data and noisy will be effectively detected based on the principles that the true signal’s distribution density will gradually decrease while noisy data’s amplitude increase.

Step 2: Decompose the processed wind speed to derive the accurate analysis. Time-frequency analysis method WT is used to decompose the original signal and reflect the similar frequency feature with respect to wind speed. Meanwhile, WT can avoid the wind speed’s local transient feature which maybe propagated over time. For instance,Daubechies (Db) wavelet of order 4 (Db4) encodes the constants and linear components.Db4 is dedicated to the analysis of the meteorological time series because it can perform appropriate trade-off ability between wavelength and smoothness.

Step 3: The proper subsets division is generated to effectively reflect the seasonal characteristics of the wind speed and satisfy the persistence of excitation for NN used for testing, which is mainly divided by the similarity and periodicity between the different seasonal characteristics.

Step 4: Lag space estimation and model robustness enhancement. Lipschitz quotient is applied to investigate the proper lag space to reflect the appropriate model structure.AdaBoosting NN is used to enhance the model robustness by utilizing the multi-network’s learning abilities. Experimental evaluation based on the dataset from NREL is given to evaluate the performance of the proposed approach.

3.2 Seasonal characteristics analysis

Usually, wind speed has a continuous spectrum to reflect the periodically change and external climates conditions. However, it is still a challenge issue to estimate the change period of the wind speed due to the complicated meteorological interaction. The seasonal characteristics of wind speed can be effectively derived based on the scalogram percentage of energy distribution. Wind speed’s trend and seasonality can be sufficiently reflected based on self-similarity related to the WT coefficient in periodogram. Note that, the energy distribution of the signal and noise is different, so wavelet filter method is used to improve the SCA accuracy. SCA results about July are intuitively displayed in Fig. 2.

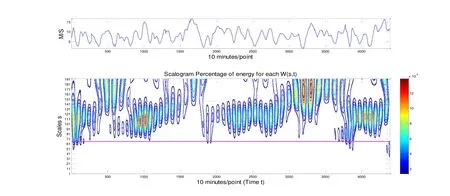
Figure 2: Seasonal characteristics analysis (July)

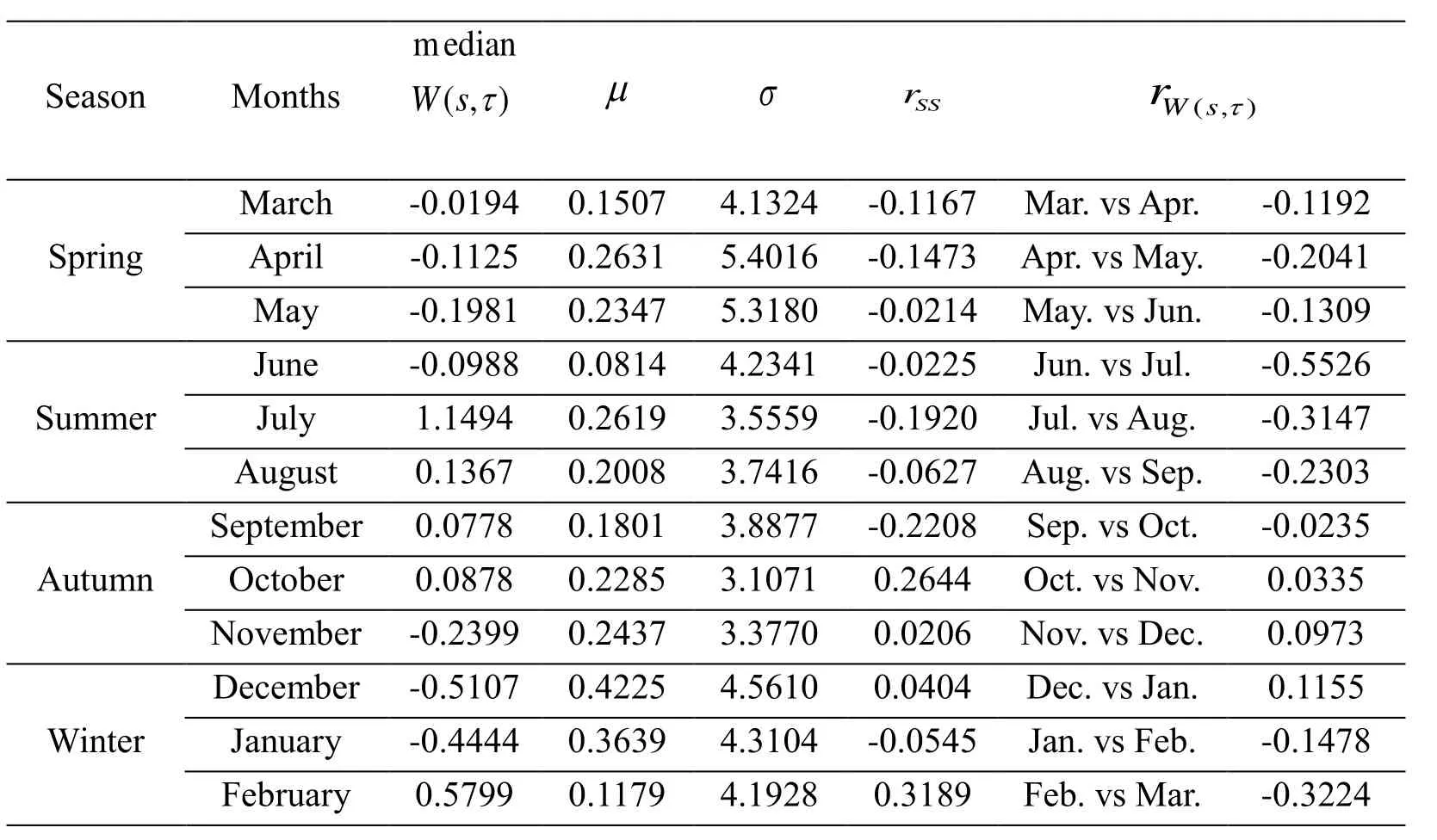
Table 1: Statistical results

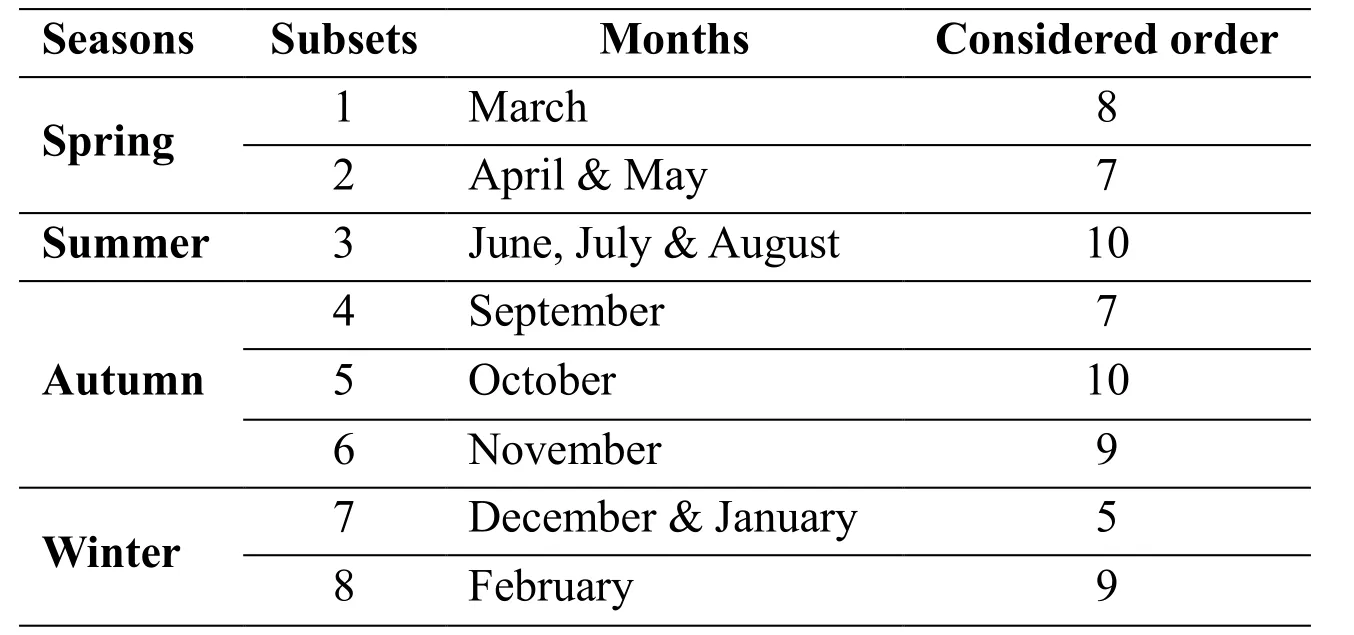
Table 2: Divided subsets based on SCA

(1) The ones related to seasons with half-day of periodic, which is seasonal and local periodicity such as summer and winter;

(2) The other one associated to the seasons is seasonal but no obvious periodicity along with time, such as the autumn and spring. The statistical results related to the wavelet coefficient matricesis given to accurately analyze the wind speed’s seasonal characteristics, given in Tab. 1.

The months are merged into one subset if the self-similar coefficientis smaller than the correlation coefficientrelated to the last and next month. In particular, June,July and August are merged into one subset due toindicates that these months have a higher similarity about seasonal characteristics than the self-similarity in each month. Based on the outlined discussion, larger sample may not benefit the establishment of the high-accuracy model unless the training sample contains the sufficient seasonal characteristics information used for testing. Wind speed’s seasonal characteristics will be sufficiently reflected in the wind speed forecasting process.

3.3 Experiments

The improper lag space cannot reflect the appropriate model structure, based on the identified inputs and outputs, the proper lag space structure associated to model orderbe accurately estimated. These model orders will be treated as the considered order in (6) based on the curve trend. More precisely, the order is selected as the model order when it is greater or equal to the knee-point where the matrix order indexflattens out along with curve trend. The estimated result for model order is shown in Tab. 3 and Fig. 3.

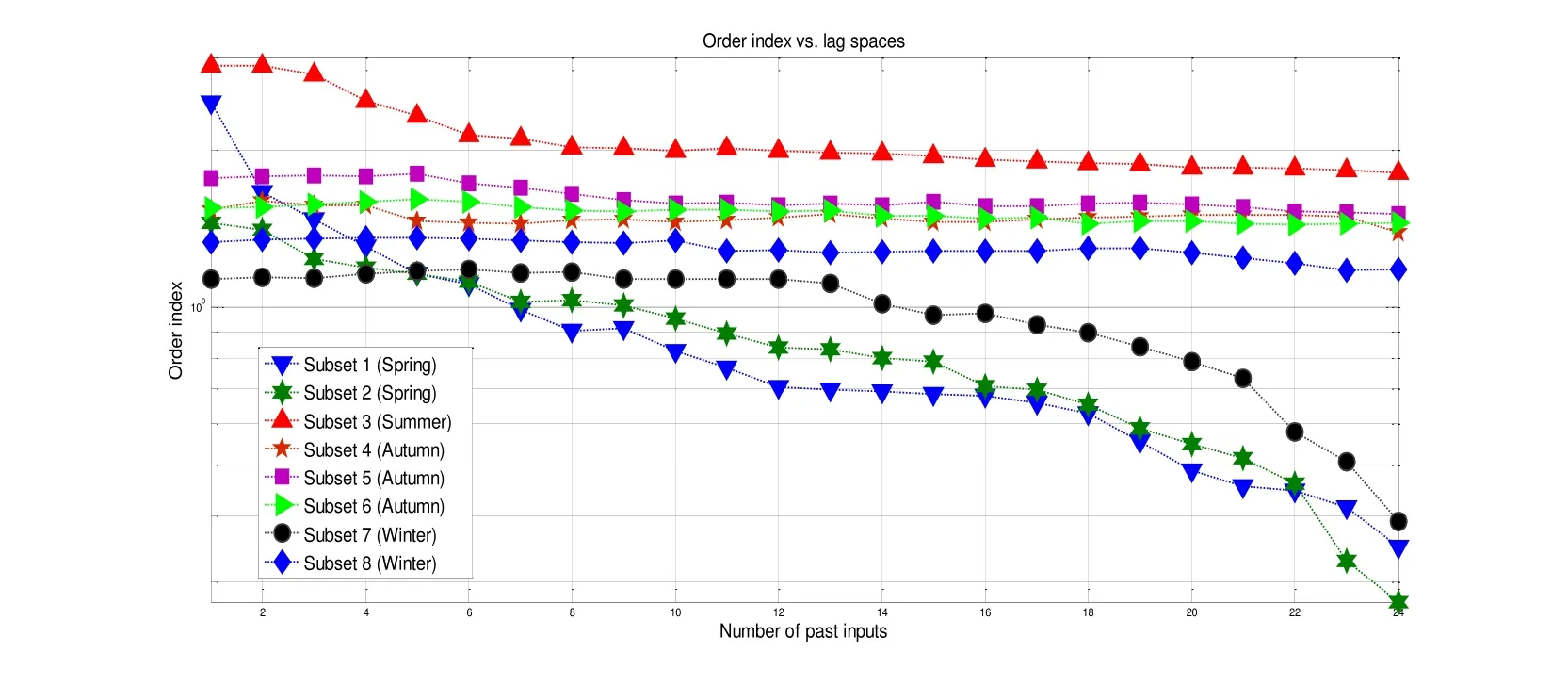
Figure 3: Model order estimation

Daubechies (Db) wavelets as one typical type of the orthogonal wavelet are usually to represent the wind speed’s complicated feature. Db4 is dedicated to the analysis of the wind speed because it can carry out appropriate trade-off ability between wavelength and smoothness. Db4 at the resolution level-2 [Shao, Deng, Cui et al. (2016)] is selected as the wavelet decomposition method to reduce the influence from the uncertainty and non-stationary in wind speed. Adaboosting NN using Levenberg-Marquardt learning algorithm is used to promote the model configuration, enhance the model robustness and improve the wind speed forecasting accuracy by utilizing the multi-individual NN’s learning abilities. This paper proposes the 24-steps (i.e. 4 h) ahead forecasting for wind speed in short-term. 60%, 20% and 20% of each subset are respectively selected as the training sample, verification sample and testing sample based on the model optimization strategy. The experimental results are validated through the cross-validation based on the forecasting results in each subset. The forecasting results are given in Tab. 3 and Fig. 4.

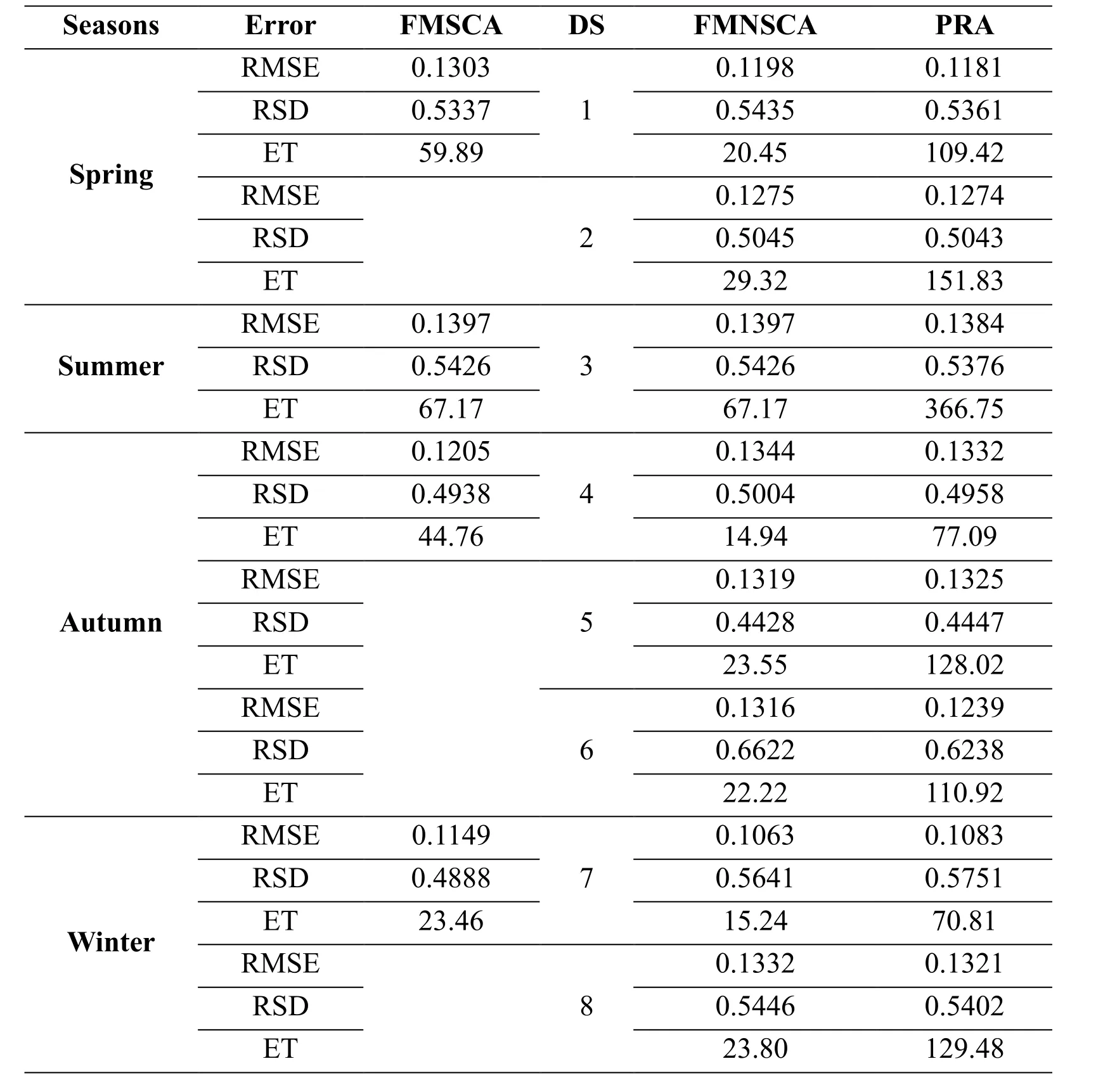
Table 3: Forecasting results

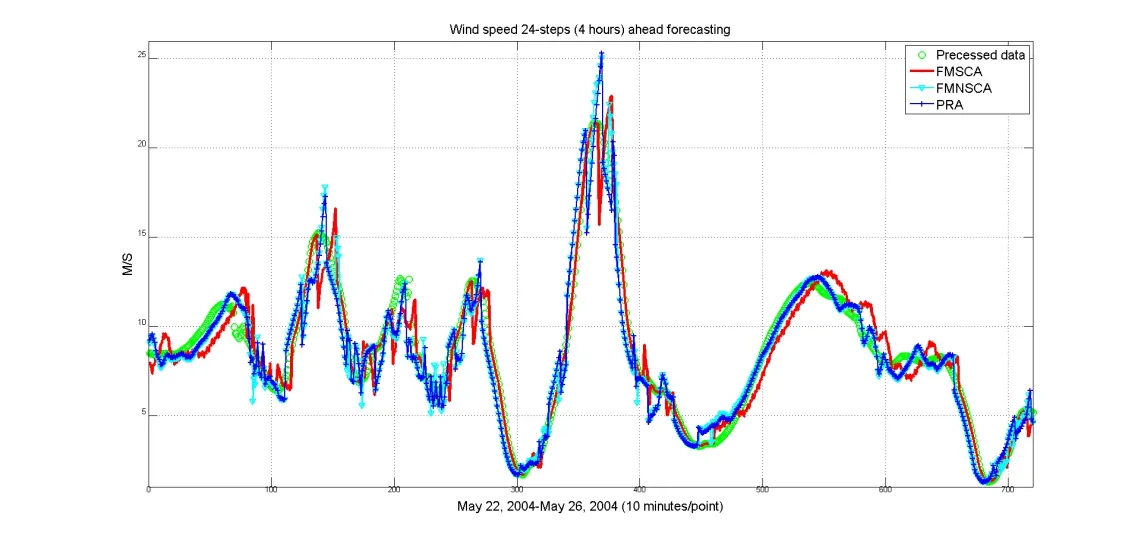
Figure 4: Forecasting results

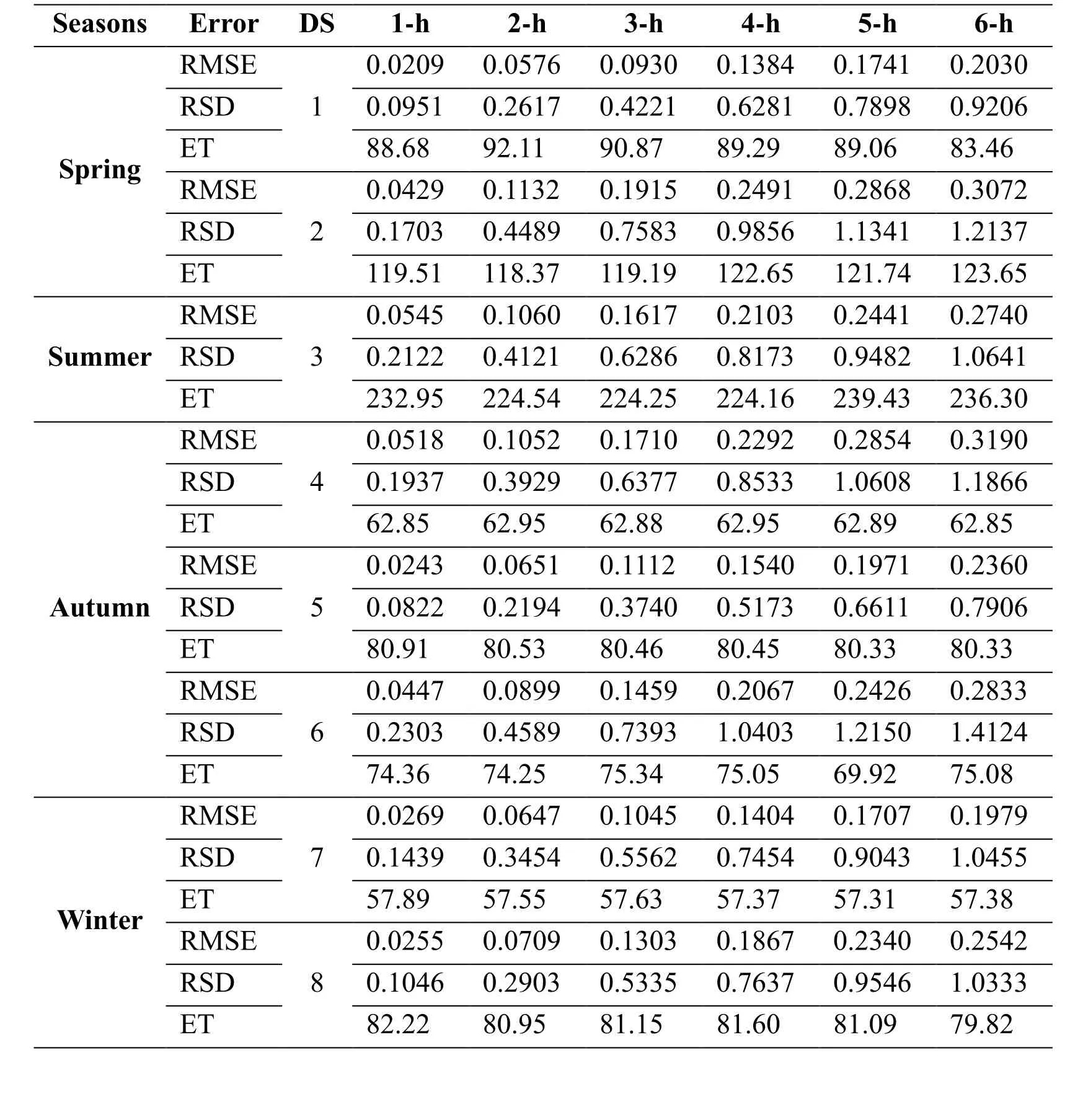
Table 4(a): Forecasting results using proposed approach

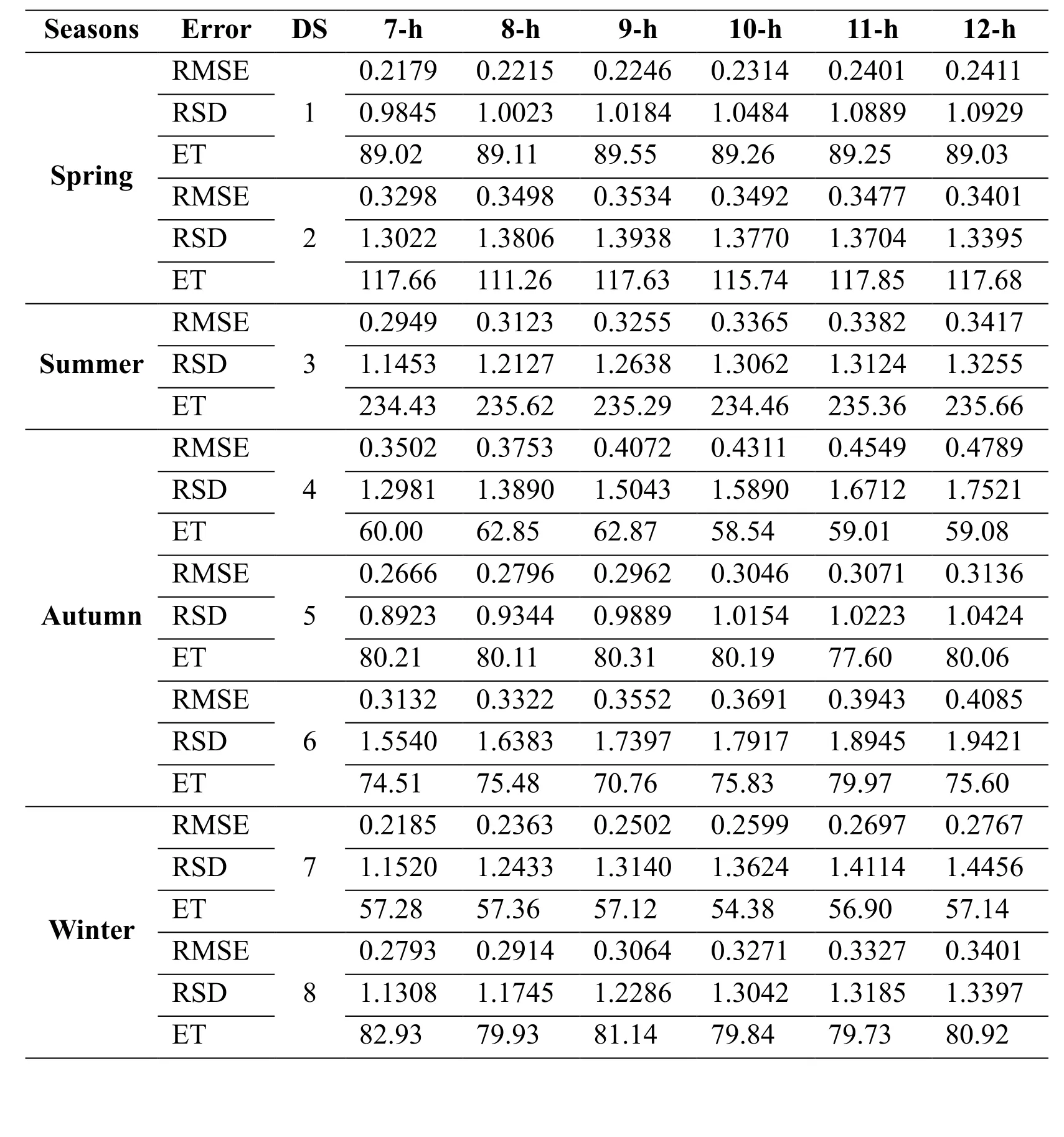
Table 4(b): Forecasting results using proposed approach

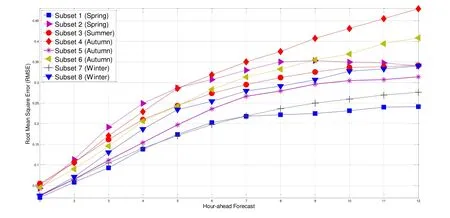
Figure 5: Wind speed hour-ahead forecast using proposed approach

Based on the outlined discussion about the experimental results, two conclusions are given:

(1) The forecasting accuracy based on the reasonable model structure and proper samples will be significantly improved based on the subsets with high similarity in seasonal characteristics. For instance, although FMSCA’s model architecture is same as the FMNSCA’s, its forecasting accuracy is still lower than the results generated by FMNSCA and PRA in general due to the insufficient seasonal characteristics analysis.

(2) The forecasting accuracy based on the reasonable model is still easily susceptible to the samples with non-uniform feature distribution. For instance, based on the statistical results, FMNSCA’s and PRA’s forecasting accuracy are higher than FMSCA on RMSE but still slightly lower than the ones based on the subsets in autumn.

(3) The forecasting performance deteriorates and the forecasting accuracy decreases along with the increment of the forecasting-steps. Typically, the small error in wind speed forecasting means the big errors in wind power forecasting. This indicates the forecasting model should have the ability of the error correction, dynamical feedback and adaptive adjustment in combination with the proposed approach in this paper.

As a conclusion, PRA can improve the forecasting accuracy related to the short-term wind speed though the approximate seasonal characteristics analysis and proper uncertainty measurement.

4 Conclusion

This paper attempted to establish a high accuracy and reliable wind speed forecasting method, taking into account wind’s seasonal characteristics and lag space. Firstly, the similarity among the different seasonal characteristics of wind speed is investigated based on self-similarity in periodogram to effectively reflect the wind speed's Seasonal distribution characteristics by properly dividing the original dataset into subsets.Secondly, the model lag space is approximately evaluated to construct the reasonable model structure. Thirdly, wavelet analysis and AdaBoosting NN are utilized to estimate the approximate frequency of wind speed and promote the model configuration. This enhances the model robustness and improves the forecasting accuracy. Experimental evaluation using the dataset from NREL in 2004 was conducted to verify the effectiveness of the proposed approach. Wavelet analysis and seasonal characteristics analysis benefit the analysis of the wind speed’s randomness and optimal neural network’s structure, respectively. AdaBoosting neural network and lag space estimation can be used to promote the model’s configuration and show the confidence in high-accuracy forecasting of short-term wind speed. In our further work, the dynamical model with ability of error correction and adaptive adjustment in combination with the proposed approach in this paper will be considered.

Acknowledgements:This project is supported by the Fundamental Research Funds for the Central Universities (No. KYLX15-0117) and Jiangsu Province Natural Science Research Projects (No. 17KJB470002).

Reference

Abd-Elaal, E. S.; Mills, J. E.; Ma, X.(2018): Numerical simulation of down burst wind flow over real topography. Journal of Wind Engineering and Industrial Aerodynamics,vol. 172, pp. 85-95.

Chang, G.; Lu, H.; Chang, Y.; Lee, Y.(2017): An improved neural network-based approach for short-term wind speed and power forecast. Renewable Energy, vol. 105, pp.301-311.

Ding, H.; Hu, Z.; Song, Y.(2012): Stochastic optimization of the daily operation of wind farm and pumped-hydro-storage plant. Renewable Energy, vol. 48, pp. 571-578.

Dowell, J.; Pinson, P.(2016): Very-short-term probabilistic wind power forecasts by sparse vector autoregression. IEEE Transactions on Smart Grid, vol.7, no. 2, pp.763-770.

Du, C.; Wang, X.; Wang, X.; Shao, C.(2016): Comprehensive value assessment of wind power by layer. IEEE Transactions on Power Systems, vol. 31, no. 2, pp.1238-1247.

Duo-Neng, L.; Zhong-Xi, H.; Zheng, G.; Xi-Xiang, Y.; Xian-Zhong, G.(2016):Permissible wind conditions for optimal dynamic soaring with a small unmanned aerial vehicle. Computer Modeling in Engineering & Sciences, vol. 111, no. 6, pp. 531-565.

Grilli, A. R.; Shumchenia, E. J.(2015): Toward wind farm monitoring optimization:assessment of ecological zones from marine landscapes using machine learning algorithms. Hydrobiologia, vol. 756, no. 1, pp. 117-137.

He, X.; Asada, H.(1993): A new method for identifying orders of input-output models for nonlinear dynamic systems. American Control Conference, IEEE, pp. 2520-2523.

Honti, M.; Scheidegger, A.; Stamm, C.(2014): The importance of hydrological uncertainty assessment methods in climate change impact studies. Hydrology and Earth System Sciences, vol. 18, no. 8, pp. 3301.

Kavousi-Fard, A.; Khosravi, A.; Nahavandi, S.(2016): A new fuzzy-based combined prediction interval for wind power forecasting. IEEE Transactions on Power Systems, vol.31, no. 1, pp. 18-26.

Megahed, A.; Moussa, A. M.; Elrefaie, H.; Marghany, Y.(2008): Selection of a suitable mother wavelet for analyzing power system fault transients. Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, 2008 IEEE, pp. 1-7.

Meng, A.; Ge, J.; Yin, H.; Chen, S.(2016): Wind speed forecasting based on wavelet packet decomposition and artificial neural networks trained by crisscross optimization algorithm. Energy Conversion and Management, vol. 114, pp. 75-88.

Ren, Y.; Suganthan, P.; Srikanth, N.(2015): A comparative study of empirical mode decomposition-based short-term wind speed forecasting methods. IEEE Transactions on Sustainable Energy, vol. 6, no. 1, pp. 236-244.

Roy, S.(2013): Power output by active pitch-regulated wind turbine in presence of short duration wind variations. IEEE Transactions on Energy Conversion, vol. 28, no. 4, pp.1018-1025.

Shademan, M.; Barron, R. M.; Balachandar, R.; Hangan, H.(2014): Numerical simulation of wind loading on ground-mounted solar panels at different flow configurations.Canadian Journal of Civil Engineering, vol. 41, no. 8, pp. 728-738.

Shao, H.; Wei, H.; Deng, X.; Xing, S.(2016): Short-term wind speed forecasting using wavelet transformation and AdaBoosting neural networks in Yunnan wind farm. IET Renewable Power Generation, vol. 11, no. 4, pp. 374-381.

Shao, H.; Deng, X.; Cui, F.(2016): Short-term wind speed forecasting using the wavelet decomposition and AdaBoost technique in wind farm of East China. IET Generation,Transmission & Distribution, vol. 10, vol. 11, pp. 2585-2592.

Sragner, L.; Horvath, G.(2014): Improved model order estimation for nonlinear dynamic systems. International Journal of Computing, vol. 2, no. 2, pp. 93-100.

Wang, J.; Song, Y.; Liu, F.; Hou, R.(2016): Analysis and application of forecasting models in wind power integration: a review of multi-step-ahead wind speed forecasting models. Renewable and Sustainable Energy Reviews, vol. 60, pp. 960-981.

Wei, H.; Shao, H.; Deng, X.(2015): Using a model structure selection technique to forecast short-term wind speed for a wind power plant in North China. Journal of Energy Engineering, vol. 142, no. 1.