基于声振法的钢混组合桥面板脱空识别研究
邹祺祺,晏班夫
(湖南大学 土木工程学院,湖南 长沙 410082)
土木工程结构中的不同材料或不同阶段施工的同类材料结合面黏结性能下降乃至分离,例如隧道衬砌、混凝土路面板、钢混组合结构及新旧混凝土结合面脱空缺陷等是常见病害。具体到桥梁工程结构,由于施工质量、后期收缩徐变、温变效应等的影响,服役中的钢管混凝土拱桥、劲性钢骨混凝土桥梁、组合结构桥梁、采用钢壳混凝土的桥塔在其钢混界面极易存在混凝土不密实、局部剥离、空洞等缺陷,并不同程度影响结构安全承载与耐久。目前常用的界面状况检测方法中,传统的声振法通过人耳识别最为简单,常用于隧道衬砌及混凝土路面板脱空的初步评判,显然受环境干扰及主观判断影响较大。通过分析激励后采集的路面振动声波信号的声学特征,即反映路面脱空位置和程度的固有频率和频率下降率的组合参数,来识别路面的脱空面积大小和位置,精度大为提高[1−4];基于瞬态冲击响应的测试方法,通过对路面瞬态振动信号的频谱分析获得路面板脱空状况信息[5]。快中子散射技术[6]、光纤光栅(FBG)传感技术[7]、冲击回波(Impactecho)法[8−9]及压电陶瓷 PZT 传感技术[10−11]也有用于钢混组合结构界面的脱空、脱黏损伤检测。钢混组合桥面板、钢管混凝土等结构由于检测面及量较大,急需一种操作简单、能够快速判别的检测方法。本文运用小波变换方法对钢混组合桥面板声振信号进行分析,根据各区域的时−频−能量特征来定性识别钢混界面脱空的程度。通过一座钢混组合结构试验桥的声振试验验证了该法的有效性。
1 脱空识别实验
1.1 缺陷设置
实验用钢混组合桥面板混凝土板厚24 cm,钢板厚为8 mm。混凝土浇筑前,在钢板上预先设置了大小不一的泡沫片与橡胶片模拟钢混界面脱空与脱空区有水或是其它介质浸入的情形(图 1和图2)。实验用泡沫及橡胶片有4种规格,即300 mm×300 mm,200 mm×200 mm,100 mm×100 mm,50 mm×50 mm,泡沫片厚度有1 mm和5 mm 2种,而橡胶片仅设置了 1 mm厚的规格。具体参数见表1。

图1 缺陷布置Fig. 1 Set-up of the styrene foam block and rubber sheet
1.2 声振测试
采用声振法用钢球对钢混桥面板脱空缺陷预埋处进行敲击,用音频范围为20~50 kHz的麦克风采集声振信号,采样频率为25.6 kHz,记录时间为45 msec。因每次敲击能量不一,在分析前对采集信号进行正规化处理,输出电压幅值限定在0.0~1.0 V以内。

图2 现场缺陷设置Fig. 2 In-situ set-up of the artificial defects
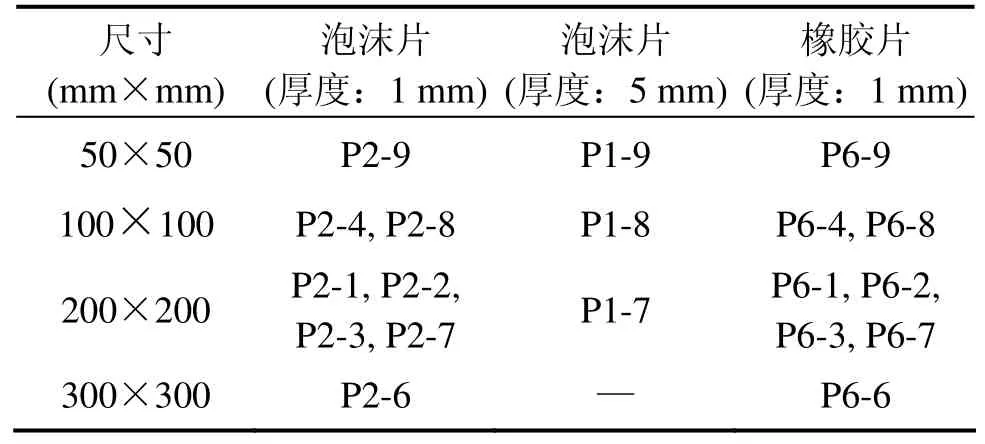
表1 缺陷设置参数Table1 Set-up of defect parameters
2 脱空识别原理
2.1 脱空识别流程
基于声振法的钢混组合桥面板界面脱空识别流程如下:
1) 根据桥面混凝土板厚度、钢板厚度等已知条件计算冲击回波共振频率及四边嵌固钢板振动频率区间,进而确定声振信号采样频率范围并选定合适的麦克风拾取信号。
2) 采用声振法用钢球对钢混桥面板脱空缺陷处进行敲击,采集组合桥面板声振信号。
3) 对声振时域信号进行小波变换,获取小波时频能量谱。
4) 根据声振信号 B区频率分布与不同尺寸钢薄板振动频率的对应关系、振动能量在A,B及C区的能量分布来确定组合桥面板是否脱空,进而大致判断脱空区大小。若有大量不同脱空缺陷样本,可以考虑用神经网络、支持向量机等分类工具来识别新样本的缺陷,如图3所示。

图3 识别流程Fig. 3 Identifying process
2.2 声振信号组成与小波分析
钢混桥面板声振信号借助钢球的瞬态锤击来实现,一般冲击信号在时域上的脉宽越窄,通过FFT变换后在频域上的频带越宽,也就是瞬态锤击可以实现宽频激励,获得较多表征结构状态的响应信息。声振信号中主要包括以下3部分:1)钢球与钢板直接接触时的金属碰撞产生的机械振动转化为声波及环境噪声;2)瞬态锤击钢混组合桥面板产生纵波(P波)、横波(S波)及瑞雷波(R波)。在冲击产生的波能中,瑞雷波占67%,横波占26%,纵波占7%,纵波传播到结构内部,被缺陷和构件底面反射回来,并产生瞬态共振,这些反射波(冲击回波)转为声波由麦克风接收;c)若钢混界面脱空,瞬态锤击将导致脱空处钢板振动并以声振形式由麦克风接收。
由于金属撞击声、环境噪声、冲击回波、钢薄板振动时频特征不一,传统的FFT频谱分析无法表征各信号的时域特性,而小波变换的多分辨度变换,能在多个尺度上分解,便于观察信号在不同尺度(分辨率)上不同时间的特性[12]。对于信号x(t)∈L2(R),其连续小波变换定义为内积:


其中:fb为带宽参数;fc为小波中心频率;j为虚数符号。参数fb和fc控制小波的形状,在时域、频域比传统的采用固定带宽fb=2的传统Morlet小波可调性更好。考虑伸缩因子a的母小波函数的傅里叶变换为:

这样由快速傅里叶变换 FFT算法求出原始识别信号和母小波函数的傅氏变换,并给出一系列伸缩因子a通过反傅里叶变换即可求得一系列的小波变换系数。注意当 a f=fc时,Ψ(af)取最大值,也就是信号频率由小波中心频率 fc和伸缩因子 a确定。
图4为拾取的声振信号时频谱示例,可知信号的时频信息特征均能通过小波分析较好地表现出来。

图4 小波时频谱Fig. 4 Time-frequency spectrum of impact acoustic signal
2.3 冲击回波
冲击回波源于弹性纵波在物件内部或外部边界之间多次反射产生共振,共振频率为:

其中:αs为被测物体形状系数,板结构可取为0.96;VP为纵波速度,本次试验测得混凝土波速约为4 500 m/s;实验用钢混组合桥面板混凝土板厚h=24 cm。这样由式(4)得到的共振频率 FT≈ 9 kHz 。图4小波时频谱上示出在9 kHz左右有振动能量,但不是特别明显。
2.4 钢薄板振动
当钢混界面脱空处钢板受到瞬态激励时,钢薄板作为声谐振子产生声音,根据弹性薄板振动理论,钢板将被激励出多个振动频率和振型,假定脱空处钢板为正方形且边界条件为四边固支时,振动频率为[12]:

其中: D=E h3/12(1 -v2)为板的抗弯刚度,ρ,E,v,h和w分别为材料的密度、弹性模量、泊松比、厚度和宽度;λmn为与模态阶数及边界条件有关的系数,具体见文献[13]和[14];fmn为模态频率。
四边简支正方形薄板振动频率为:
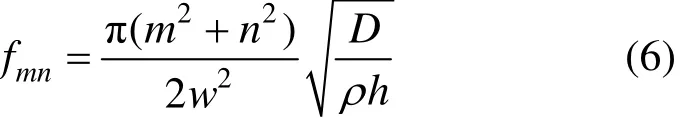
表2表示实验中对于不同的正方形缺陷设置,脱空处钢板瞬态激励后按式(5)得到的声振频率。表3表示按式(6)得到的声振频率。
本文仅示出f23阶以下模态,由表2和表3可以看出,脱空面积越大,钢薄板振动基频下降越多,对于300 mm×300 mm规格钢板,低频谐振频率分布较密,当尺寸下降至100 mm×100 mm规格,对于简支边界的情形,仅有前两阶频率在10 kHz分析频率范围以内。当脱空尺寸过小(50 mm×50 mm规格),谐振基频已经在分析频率范围10 kHz以外。也就是根据钢板谐振频率在分析范围内的峰值个数及基频大小可以大致判断脱空的有无,由于脱空处钢板实际边界条件介于嵌固与简支之间,而且脱空形态各一(文中仅给出正方形缺陷形式下的频率计算结果),从谐振频率分布特点还较难定量识别出脱空面积。
2.5 特征抽取
如图5所示,对声振信号主要组成部分的分析表明,小波时频谱可分为3个表征信号内容的区域,即表征混凝土质量、板厚度等信息的冲击回波高频共振A区、表征脱空区钢板自振特征的B区及表征环境噪声条件及大面积脱空板振动的低频C区。3区频率的分布与板的脱空与否密切相关,另一方面,从小波时频谱图上还可获取板的冲击回波高频区信号衰减与钢薄板振动特征信号衰减信息,但以上时域信息反映的是混凝土板的质量及钢薄板的阻尼信息,对钢混组合界面的脱空判别意义不大。本文将A,B和C 3区的正规化能量分布Fi作为识别特征,即

表2 四边嵌固钢薄板振动频率Table 2 Vibration frequency (kHz) of the clamped rectangular steel plate with respect to the plate size
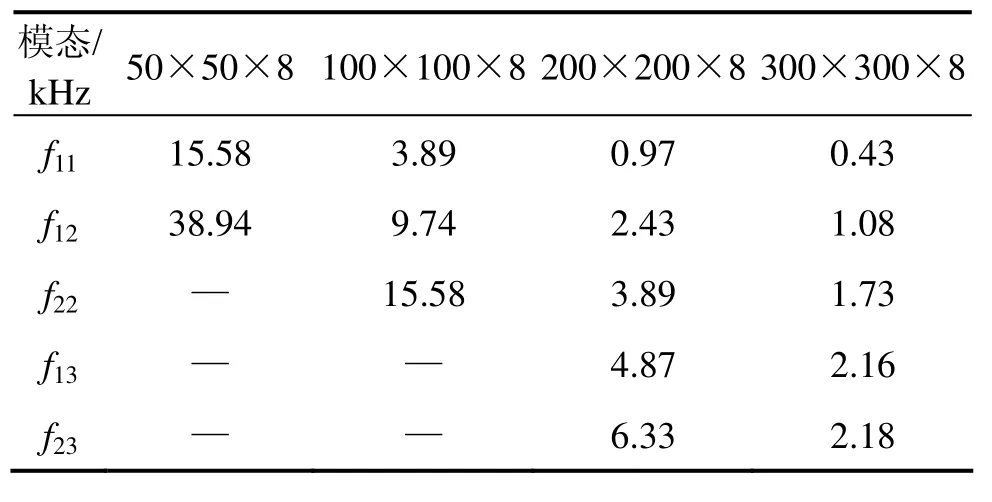
表3 四边简支钢薄板振动频率Table 3 Vibration frequency (kHz) of the simply supported rectangular steel plate with respect to the plate size

其中:(,)Wft为以时频谱形式表示的小波变换系数;Ei是频带Zi(i=A, B, C 3区)的振动能量。

图5 小波时频谱特征抽取Fig. 5 Feature extraction of wavelet spectrum of impact acoustic signal
3 识别结果
具体到本次实验,A区冲击回波共振频率在 9 kHz左右,确定A区频带为8 kHz到10 kHz,B区钢薄板振动频带确定为1 kHz到8 kHz,表征环境噪声条件及大面积脱空板振动的低频C区振动频带确定为0 kHz到1 kHz。

图6 小波时频谱(泡沫片)Fig. 6 WT-based data analysis results (styrene foam block)
图6和图7为4种厚度均为1 mm,但规格不同的预埋泡沫片及橡胶片区域对应的典型声振信号小波时频谱,图8~10为50个测试样本的分区能量分布,其中包括4个未脱空测试样本,26个已知缺陷测试样本(预埋泡沫片或橡胶片,尺寸已知),20个尺寸未知缺陷测试样本(预埋泡沫片,有缺陷,但尺寸未知),可以看出:1) 对于预埋泡沫片模拟钢混界面脱空的情形,A,B和C 3区声振频率及能量分布很直观地显示了不同脱空尺寸的钢板振动特征,比如,300 mm×300 mm规格钢板P2-8的B区振动频率峰值较多,典型的有1.32,2.6,3.72,4.35,5.37和7.41 kHz等,这与表2和表3所示的四边嵌固及简支正方形钢薄板振动频率计算值在B区分布较多是一致的;同样,200 mm×200 mm规格钢板对应的1.42,2.51,4.24,5.22,6.62 kHz与表3的计算值0.97,2.43,3.89,4.87 kHz对应较好;当缺陷区尺寸减为100 mm×100 mm规格,四边嵌固钢薄板振动计算基频为3.89 kHz,第2阶9.74 kHz已经超出B区分析范围,与图6所示同样规格钢板P2-8的B区仅分布一4.03 kHz峰值是相符的。当缺陷尺寸减小至50 mm×50 mm规格,由于简支条件下的计算基频15.58 kHz已经大大超出分析范围,这与图6所示同样规格钢板P2-9的B区无峰值分布是完全一致。
2) 如图7所示,对于预埋橡胶片模拟脱空区有水或是其他介质浸入的情形,由于橡胶片的吸能作用,无论缺陷尺寸如何变化,其B区并无任何峰值存在,钢板振动能量完全吸收,振动能量主要分布于A和C区。

图7 小波时频谱(橡胶片)Fig. 7 WT-based data analysis results (rubber sheet)
3) 如图8和图9所示,从声振信号能量分布的角度来看,对于未脱空处,B区占据25%~40%能量;对于预埋泡沫片的情形,300 mm×300 mm,200 mm×200 mm,100 mm×100 mm 3种规格脱空处能量分布相近,B区钢薄板振动占据70%~90%能量,而50 mm×50 mm规格脱空处,B区钢薄板振动占据0%~15%能量,这是由于计算基频已经超出了分析范围;而对于预埋橡胶片的情形(模拟脱空区有水或是其它介质浸入),B区占据0%~10%能量,这是由于钢薄板振动能量被橡胶片吸收。
4) 对B区钢薄板振动能量占比设定健康区间,当测试样本的B区钢薄板振动能量占比处于健康区间内时,认为该区域未发生脱空;当能量占比高于上限值,可认为该区域发生脱空;当能量占比低于下限值时,可认为该区域脱空区域较小或者被其他介质浸入。
5) 在已知缺陷样本中,如图 8所示,泡沫-12号样本为200 mm×200 mm规格脱空处,其B区能量分布占比为 21%,与预估能量占比 70%~90%有较大出入,因此泡沫-12号样本识别结果不可信,同理,泡沫-17号样本识别结果不可信;如图9所示,在橡胶片样本识别结果中,橡胶-8号样本识别结果不可信。

图8 识别结果(泡沫片)Fig. 8 Identification results (styrene foam block)

图9 识别结果(橡胶片)Fig. 9 Identification results (rubber sheet)
6) 图10为尺寸未知缺陷样本(预埋泡沫片,有缺陷,但尺寸未知)的 3区能量占比。未知-9,11和19号测试样本的B区能量占比处于健康区间内,识别结果为未脱空,与实际不符,不可信。
7) 由于声振信号的收集过程中容易受到环境因素的干扰,因此基于声振法的脱空识别需要考虑识别成功率。表4给出了本实验中根据50个实测样本得到的识别率,可以看出,识别率在85%以上,有潜力应用于实际工程。

图10 识别结果(待识别样本)Fig. 10 Identification results (samples)

表4 识别结果Table 4 Identification results
4 结论
1) 声振法作为一种简单有效的现场无损测试方法,可用于钢混组合桥面板脱空缺陷的检测,其工作原理是通过瞬态锤击组合桥面板实现宽频激励,获得较多表征结构状态的响应信息,钢混界面出现脱空时,声振信号的谐振频率分布及振动能量分布发生明显变化,据此可以定性判断脱空是否发生,并大致判断脱空区范围。
2) 本文运用小波变换方法对钢混组合桥面板声振信号进行分析,将小波时频谱分为3个表征信号内容的区域,即表征混凝土质量的冲击回波高频共振A区、表征脱空区钢板自振特征的B区及表征环境噪声的低频C区,根据各区域的时−频−能量特征设定B区能量占比健康区间,可以定性识别钢混界面脱空。
3) 在一座钢混组合结构试验桥施工时预埋了大小不一的泡沫与橡胶片模拟钢混界面的脱空与脱空区有水或是其它介质浸入的情形,声振测试试验验证了该法的有效性,声振测试的识别率在85%以上,有潜力应用于实际工程。
4) 对于低频 C区下一步研究可采用小波分析等工具进行更精细分析,提取表征脱空区有水或是其他介质浸入时的特征信息。
参考文献:
[1] 薛忠军, 王佳妮, 张肖宁. 基于Fisher函数的水泥路面板底脱空判别方法[J]. 振动与冲击, 2013, 32(17): 171−176.XUE Zhongjun, WANG Jiani, ZHANG Xiaoning.Discrimination method for cement road slab void based on fisher function[J]. Journal of Vibration and Shock,2013, 32(17): 171−176.
[2] ZHANG G, Harichandran R S, Ramuhalli P. Automatic delamination detection of concrete bridge decks using impact signals[J]. Journal of Bridge Engineering, 2012,17(6): 951−954.
[3] ZHANG G, Harichandran R S, Ramuhalli P. An automatic impact-based delamination detection system for concrete bridge decks[J]. Ndt & E International, 2012, 45(1):120−127.
[4] 王楠. 声振法检测混凝土路面脱空的信号处理方法研究[D]. 西安: 长安大学, 2012.WANG Nan. Acoustic vibration of concrete pavement void detection signal processing method[D]. Xi’an:Chang’an University, 2012.
[5] 王骑, 韩西, 易志坚. 混凝土路面板下脱空识别的瞬态冲击响应法研究[J]. 公路交通科技, 2010, 27(11):26−32.WANG Qi, HAN Xi, YI Zhijian. Study on identification of cavity area under concrete pavement using transient impulse-response method[J]. Journal of Highway and Transportation Research and Development, 2010, 27(11):26−32.
[6] 易瑞吉. 钢板与浇注砼结合面脱空缺陷中子无损探测及结果数字显像方法研究[D]. 南京: 南京水利科学研究院, 2007.YI Ruiji. Study on non-destructive testing and digitization image-display method using fast neutron for cavity defects in interfaces between steel plate and pour concrete[D]. Nanjing: Nanjing Hydraulic Research Institute, 2007.
[7] 刘宏月. 光纤光栅传感器在结构健康监测中的应用研究[D]. 南京: 南京航空航天大学, 2012.LIU Hongyue. Research on the health monitoring of material structure using fiber grating[D]. Nanjing:Nanjing University of Aeronautics and Astronautics,2012.
[8] Yehia S, Abudayyeh O, Nabulsi S, et al. Detection of common defects in concrete bridge decks using nondestructive evaluation techniques[J]. Journal of Bridge Engineering, 2007, 12(2): 215−225.
[9] Watanabe T, Morita T, Hashimoto C, et al. Detecting voids in reinforced concrete slab by SIBIE[J].Construction & Building Materials, 2004, 18(3): 225−231.
[10] 许斌, 李冰, 宋刚兵, 等. 基于压电陶瓷的钢管混凝土柱剥离损伤识别研究[J]. 土木工程学报, 2012, 45(7):86−96.XU Bin, LI Bing, SONG Gangbing, et al. Detection of the debonding defect of concrete-filled steel tubes with piezoceramics[J]. China Civil Engineering Journal, 2012,45(7): 86−96.
[11] 许斌, 陈梦琦. 基于压电阻抗的钢管砼柱横隔板剥离缺陷检测[J]. 压电与声光, 2015, 37(1): 172−175.XU Bin, CHEN Mengqi. Interface debonding of diaphragm for large-scale irregular CFST column based on electro-mechanical impedance ofPZT[J].Piezoelectrics & Acoustooptics, 2015, 37(1): 172−175.
[12] QIAN Shie. Introduction to time-frequency and wavelet transforms[M]. China Machine Press, 2005.
[13] 曹志远. 板壳振动理论[M]. 北京: 中国铁道出版社,1989.CAO Zhiyuan. Vibration theory of plates and shells[M].Beijing: China Railway Publishing House, 1989.
[14] 钟阳, 张永山. 四边固支弹性矩形薄板的自由振动[J].动力学与控制学报, 2005, 3(2): 66−70.ZHONG Yang, ZHANG Yongshan. Free vibration of rectangular thin plate with completed clamped supported[J]. Journal of Dynamics and Control, 2005,3(2): 66−70.

