全长黏结式注浆锚杆侧摩阻力分布实用简便计算

熊辉，皮乐

(湖南大学 土木工程学院，湖南 长沙 410082)

锚杆是一种有效的地下、边坡支护技术，具有结构受力均匀合理、施工便捷、工期短、造价低等优点，已在国内外得到广泛应用[1]。锚杆从加载到失效需要经历弹性加载和滑移破坏2个阶段[2]；随着外部荷载加大，锚杆变形逐渐加大，锚固力也随之加大；直至达到抗拔极限承载力，锚杆开始出现滑移并失效。目前，国内外学者对锚杆抗拔机理作了大量实验及理论研究：周勇等[3]通过引入锚杆预应力损失剩余系数的概念，推导出了锚杆变形的计算公式、锚杆预应力的确定方法。对工程算例分析后，提出了确定锚杆设计参数合理的建议。REN等[4]假定锚固界面剪切应力与位移呈3折关系，建立了弹性、弹塑性以及全塑性状态下锚固段界面摩擦应力分布解。黄明华等[5]从锚杆拉拔试验的荷载位移曲线出发，建立锚固界面的非线性剪切滑移模型以及锚杆锚固段荷载传递的非线性微分方程，获得了锚杆锚固段的轴力和界面剪应力解析解。现有理论研究普遍存在推导过程复杂，结果采用隐函数等问题，对工程人员来说有一定的运算困扰。因此本文在对锚杆进行分段分析时，运用基本的材料及理论力学知识对其进行分析求解，得到了锚杆摩阻力分布的2重级数数学表达式。

1　侧摩阻力计算公式的建立

1.1　锚杆受力变形机理

锚杆体、注浆体及岩土体三者耦合作用[6]状态时，综合形成一个变形协调体。将其整体切出来，分成n个微段，每个微段都由l长度的锚杆体、注浆体和岩土体组成(如图 1所示)，后者可以根据其抗剪刚度简化为切向弹簧，刚度系数为 K=SK2=2πrlK2。王伟的试验研究结果表明砂浆抗剪刚度约为3 GPa/m[7]；Odah等[8]给出了不同岩体的抗剪刚度K2，对比可知：对于土体锚杆，砂浆的抗剪刚度远大于土体的抗剪刚度。因此在设计中常常忽略锚杆和注浆体的相对位移，将锚杆体和注浆体组成的复合杆体作为锚固体[9]，锚固体弹性模量为两者按截面面积加权：E=(EgAg+EaAa)/(Ag+Aa)[10]，锚杆体与注浆体弹性模量和横截面积分别为 Eg，Ea，Ag和Aa。按前人研究的理论成果，三者受力变形分布沿锚杆长度近似成指数[11−12]或双曲线[13]变化，锚端受力变形明显，底部不明显。

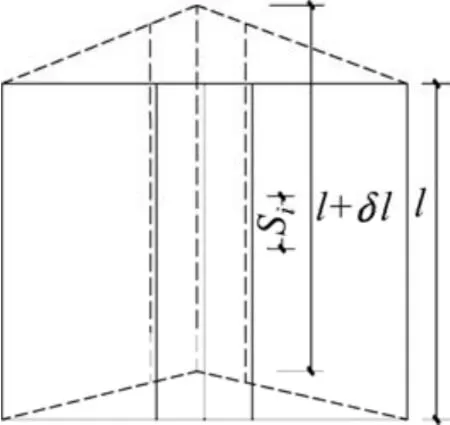
图1　分段变形示意图Fig. 1　Schematic diagram of sectional deformation

2.2　荷载传递基本方程

一注浆锚杆长为 L，半径为 r；岩土体为密实均质黏结性能较好的土体；对变形协调体进行n段划分，每一段长度为l，即l=L/n。

对于任一锚杆分段 i，侧面受到总摩阻力为 Pi的均匀分布力作用，下端受到其下方所有分段外侧摩阻力之和作用，上端则受到包括自身在内的所有分段外侧摩阻力之和作用，分段受力分析图及轴力图分别如图2和图3所示。

图2　分段锚固体受力分析图Fig. 2　Stress analysis diagram of segmented anchor

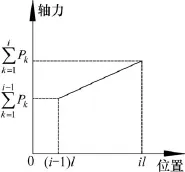
图3　第i段锚杆轴力图Fig. 3　Section i anchor solid shaft

由于锚固体的受力变形为线性关系，因此第 i段锚固体的变形图也是线性变化，如图4所示。

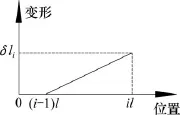
图4　第i段锚固体变形图Fig. 4　Section i anchor solid deformation diagram

锚固体分段i变形长度为δli；分段锚固体中点位移值为Si；与此对应的岩土体变形为Δi，等于分段锚固体中点位移值Si，即：Δi=Si；受力分析如图5所示。

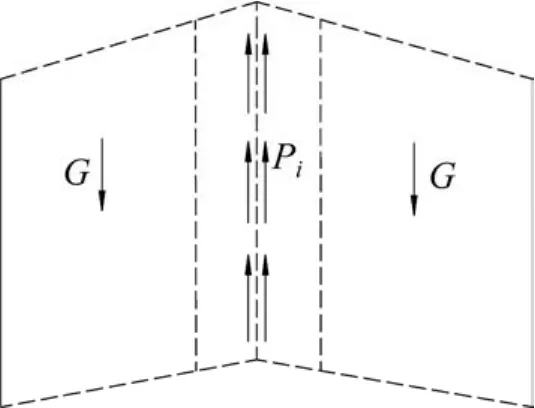
图5　分段对应岩土体受力变形图Fig. 5　Sectional stress and deformation map of rock and soil

由上述分析有如下式：

式中：P为张拉端总荷载；Pi为第i段锚固体外侧所受侧摩阻力值。

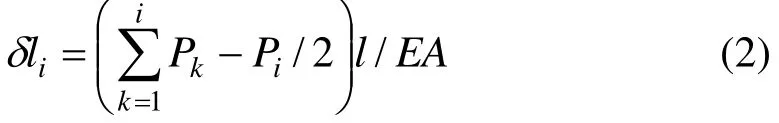
式中：ilδ为第i段锚杆变形值；l为分段长度；EA为锚杆等效拉压刚度。

式(2)：由于分段内轴力是线性变化(如图 3)，故其应变值也是线性变化。因此可用中点应变值与第i段锚杆长度乘积得到i段锚杆变形值。

式中：Si为第i段锚固体位移值。

式(3)：由于分段内变形的线性变化，故考虑取该分段锚固体中点变形值——平均值作为分段位移值较合理。因此其值为包括该分段在内的下部所有分段变形值之和减去该分段自身变形值的一半。

式中：Δi为岩土体变形值；K为分段岩土体变形刚度系数。

2.3　摩阻力计算结果推导及分析

由式(2)，(3)和(5)有：

式中：B和D为表达式简化参数；r为注浆锚杆体半径；K2为岩土体抗剪刚度。

为简化计算对锚杆进行5段划分，如图6所示。

图6　锚杆5段划分示意图Fig. 6　Sketch map of five section of anchor bolt

由式(1)及式(6)计算得：

2　实例验证

杨庆等[13]建立了注浆锚杆界面剪应力计算方程，并对影响锚杆锚固效果的参数进行分析，合理地得到了全长注浆锚杆的界面剪应力和轴向载荷的双曲线分布函数。该文对岩体的适用范围包括岩石、砂砾以及黏土等，因此，选择该文理论作实例验证。

一锚杆长3 m，直径0.2 m；采用M7强度水泥砂浆，内置3根Φ20钢；岩体为黏土，抗剪强度取600 MPa/m；张拉端荷载P=180 kN。

由文献[13]和本文分别计算的分段侧摩阻力 Pi及位移Δi结果如下表所示：

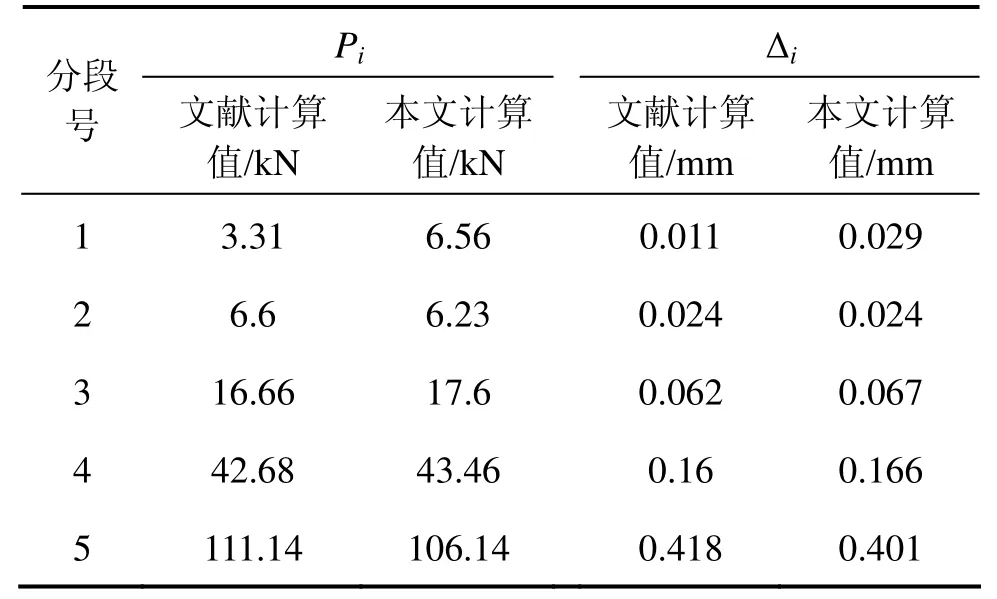
表1　锚杆5分段时，文献[13]与本文公式计算的侧摩阻力和位移值对比表Table 1　When the anchor is in the fifth section, the comparison of the side friction and displacement calculated by the formula [13]

对比可知，除底部第一分段外，由本文计算出的摩阻力分布结果和分段锚固体位移值计算结果与文献相应计算结果符合度都非常高。其中分段摩阻力分布相差不超过 5%；位移计算值相差不超过7%，精度满足工程计算要求。

图7　5分段锚杆摩阻力分布与位移计算值与文献计算值对比Fig. 7　Comparison of calculated values of displacement distribution and displacement of five section anchor bolt with calculated value of literature

3　对计算结果影响因素的分析

在实例中各参数的基础上控制变量，分别对侧摩阻力计算的影响因素进行分析，得到 4.1~4.5节中的结论。

3.1　不同分段情况对计算结果的影响

将变形协调体分为3段，其他参数不变，进行分析，由式(1)及式(6)得：

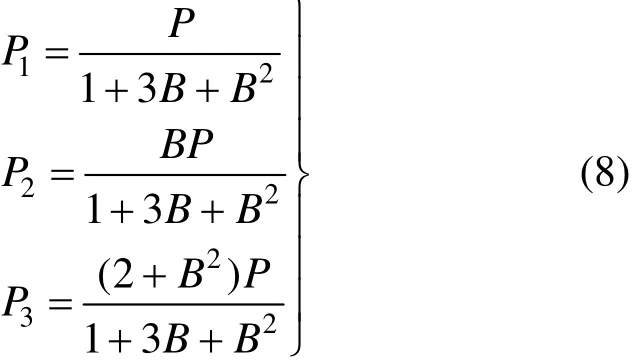
由文献[13]和本文分别计算的分段侧摩阻力 Pi及位移Δi结果如下表所示：

对比可知由本文计算出的摩阻力分布结果与文献计算出的摩阻力分布结果符合度也较高，相差不超过10%；位移计算结果相差较大，达到了20%。

将变形协调体分成7段进行分析：

表2　锚杆3分段时，文献[13]与本文公式计算的侧摩阻力和位移值对比表Table 2　When the anchor is in the three section, the comparison of the side friction and displacement calculated by the formula [13]

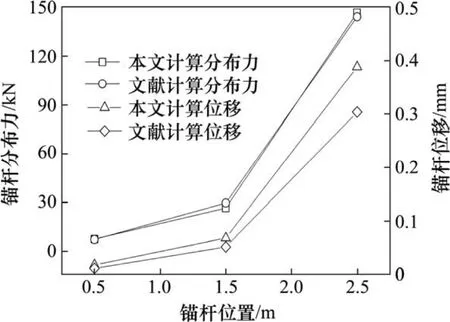
图8　3分段锚杆摩阻力分布与位移计算值与文献计算值对比Fig. 8　Comparison of calculated values of displacement distribution and displacement of three section anchor bolt with calculated value of literature

由式(1)及式(6)得：

由文献[13]和本文分别计算的分段侧摩阻力及位移结果如表(3)所示。

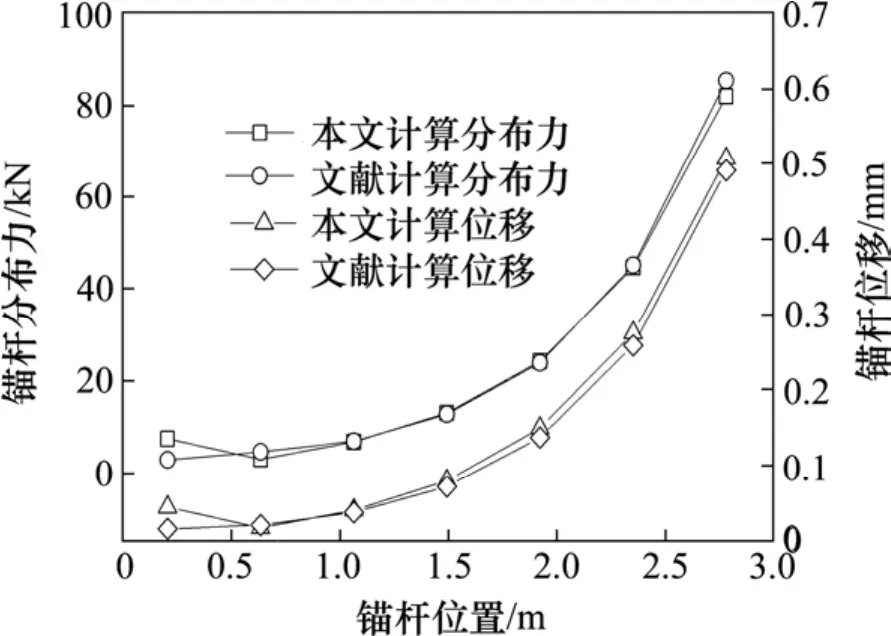
图9　7分段锚杆摩阻力分布与位移计算值与文献计算值对比Fig. 9　Comparison of calculated values of displacement distribution and displacement of seven section anchor bolt with calculated value of literature

对比可知，除底部两段外，由本文计算出的摩阻力分布结果和分段锚固体位移值计算结果与文献相应计算结果符合度都非常高。其中分段摩阻力分布相差不超过4%；位移计算值相差不超过6%，精度满足工程计算要求。

综上所述，用本文方法计算锚杆侧摩阻力分布，分段3，5和7段时，结果与文献计算结果符合度逐渐提高，分段越多，精确度越高。

3.2　锚固体直径D对计算结果的影响分析

假定锚杆直径分别为0.1，0.17，0.24，0.3，0.34和 0.4 m，其他参数不变，通过计算得到各分段总侧摩阻力占比情况，如图10所示。

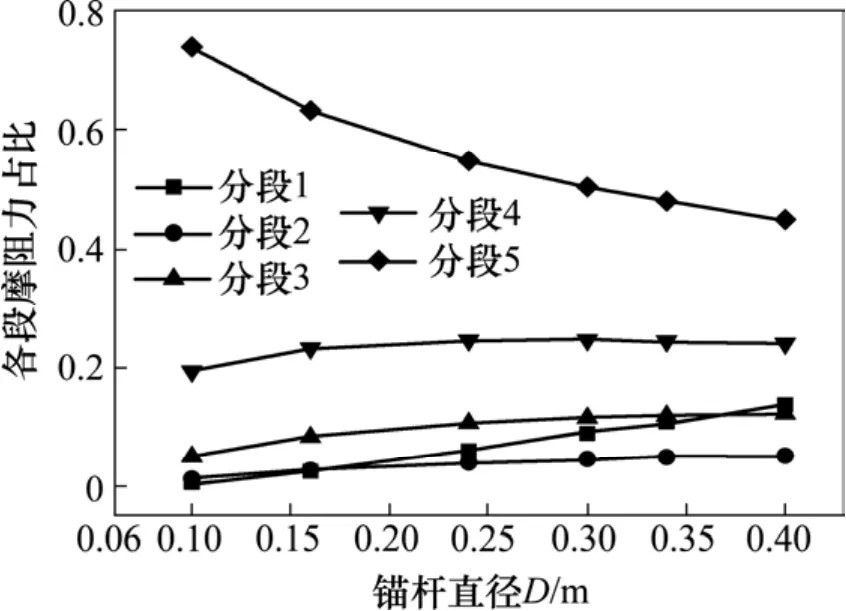
图10　5分段时，锚杆直径D对各分段侧摩阻力分布影响Fig. 10　When the five segments the influence of bolt diameter D on the distribution of lateral friction resistance

由图得出的是随锚杆直径增大锚杆各分段侧摩阻力抵抗荷载比例情况，可看出分段5侧摩阻力占比随锚杆直径增大而减小，其他分段占比逐渐缓慢增加，分段1增加最快。

4.3　土体抗剪刚度K2对计算结果的影响分析

假定土体抗剪刚度分别为 2，4，6，8，10和12(×108Pa)，其他参数不变，通过计算得到各分段总侧摩阻力占比情况，如图11所示。

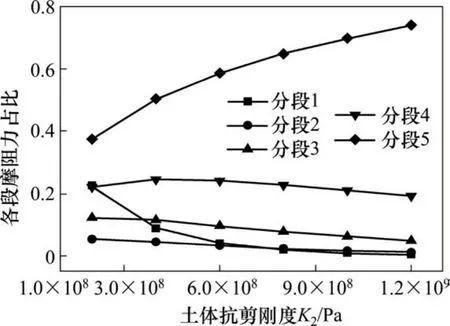
图11　5分段时土体抗剪刚度K2对各分段侧摩阻力分布影响Fig. 11　When the five segments the influence of shear stiffness K2 of soil on the distribution of lateral friction resistance

由图得出的是随土体抗剪刚度增大锚杆各分段侧摩阻力抵抗荷载比例情况，可看出分段5侧摩阻力占比随土体抗剪刚度增大而增大，其他分段占比逐渐缓慢减小，分段1减小最快。

4.4　锚固体等效弹性模量 E对计算结果的影响分析

假定锚固体等效弹性模量分别为 4.04，5.11，6.31，12.6和19.7 GPa，其他参数不变，通过计算得到各分段侧摩阻力占比情况，如图12所示。

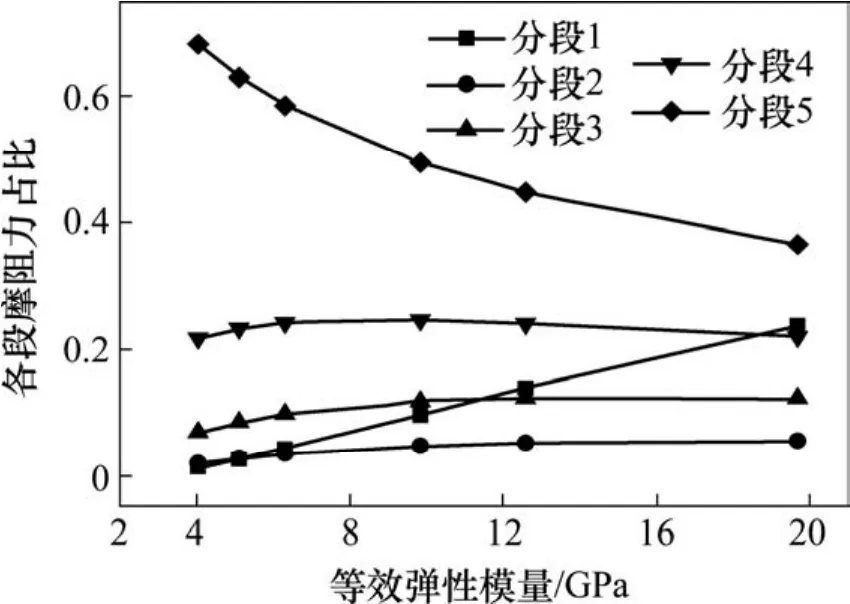
图12　5分段时等效弹性模量对各分段侧摩阻力分布的影响Fig. 12　When the five segments the influence of equivalent elastic modulus on the distribution of lateral friction resistance

由图得出的是随等效弹性模量增大锚杆各分段侧摩阻力抵抗荷载比例情况，可看出分段5侧摩阻力占比随等效弹性模量增大而减小，其他分段占比逐渐缓慢增大，分段1增大最快。

4.5　参数B对计算结果的影响分析

由式(6)可知参数B是一个综合参数。影响参数B的因素有：锚杆分段数、锚固体直径D、土体抗剪刚度K2及锚固体等效弹性模量E。前面已分别单独分析了各因素对侧摩阻力分布计算的影响，但实际中经常多因素同时作用，所以本节通过分析综合参数B对侧摩阻力分布的影响来分析多因素同时作用时对计算结果的影响，如图13所示。

可以看出，当0＜B＜0.17时：侧摩阻力占比由大到小顺序依次为：第1段(底部分段)、第5段(靠近端部分段)、第4段、第3段和第2段。当B≥0.17时，第5段占比最大，第1段则随B值的增大而减小，当B≥1时，第1段占比小于第2段。

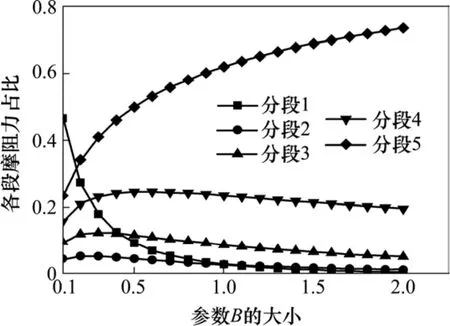
图13　5分段时参数B的值对锚杆各分段摩阻力占荷载的比例的影响Fig. 13　When the five segments the influence of the subsection parameter value of B on the proportion of the frictional load of each segment of the anchor

4　结论

1) 锚杆侧摩阻力从底部到端部呈 2重级数分布，靠端部长度的40%消耗了张拉荷载的85%，靠近底部几乎为 0；位移的分布与摩阻力的分布形式一致。

2) 锚杆分段数越多，计算结果精确度越大。当分 3段计算时，计算结果与文献[13]计算值相差达到10%~20%；当分5段计算时，结果相差5%~6%；当分7段计算时，结果相差4%~5%。分段数越多，计算量越大，具体分多少段需要根据实际工程精度需求而定。

3) 锚杆直径 D(注浆体)与等效弹模 E(配筋)越大，摩阻力的分布集中于杆端现象趋向弱化，下部各分段占比上升；土体抗剪刚度K2越大，摩阻力的分布集中于杆端现象加强，下部摩阻力分布占比减少。

4) 表达式中参数 B的值越小，锚杆底部分段抵抗张拉荷载的贡献值越大。当B＜0.17时，底部分段贡献值最大；0.17≤B＜1时，靠近端部分段贡献值最大，底部分段贡献值还是大于倒数第2段；当B≥1时，底部分段贡献值最小。

5) 对于边坡稳定加固以及基础抗浮设计，本文提供了一种实用的计算方法。

参考文献：

[1] 张明义, 张健, 刘俊伟, 等. 中风化花岗岩中抗浮锚杆的试验研究[J]. 岩石力学与工程学报, 2008, 27(增 1):2741−2746.ZHANG Mingyi, ZHANG Jian, LIU Junwei, et al.Experimental investigation on anti-floating anchor in moderatery weathered granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(Suppl 1):2741−2746.

[2] 黄明华, 周智, 欧进萍. 拉力型锚杆锚固段拉拔受力的非线性全历程分析[J]. 岩石力学与工程学报, 2014,33(11): 2190−2199.HUANG Minghua, ZHOU Zhi, OU Jinping. Nonlinear full-range analysis of load transfer in fixed segment of tensile anchors[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(11): 2190−2199.

[3] 周勇, 朱彦鹏, 任永忠. 预应力锚杆柔性支护体系中锚杆的变形[J]. 中国铁道科学, 2015, 36(3): 58−65.ZHOU Yong, ZHU Yanpeng, REN Yongzhong. Anchor deformation of flexible supporting system with prestressed anchors[J]. China Railway Science, 2015,36(3): 58−65.

[4] REN F F, YANG Z J, CHEN J F, et al. An analytical analysis of the full-range behavior of grouted rock bolts based on atri-linear bondslip model[J]. Construction and Building Materials, 2010, 24(3): 361−370.

[5] 黄明华, 周智, 欧进萍. 全长黏结式锚杆锚固段荷载传递机制非线性分析[J]. 岩石力学与工程学报, 2014,33(增 2): 3992−3997.HUANG Minghua, ZHOU Zhi, OU Jinping. Nonlinear analysis on load transfer mechanism of wholly grouted anchor rod along anchoring section[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Suppl 2):3992−3997.

[6] 漆泰岳, 陆士良. 锚杆单元模型及其应用[J]. 中国矿业大学学报, 2003, 32(5): 524−529.QI Taiyue, LU Shiliang. Model of bolt element and its application[J]. Journal of China University of Mining &Technology, 2003, 32(5): 524−529.

[7] 王伟. 砂浆抗剪强度参数的试验研究[J]. 水利与建筑工程学报, 2005, 3(4): 30−32.WANG Wei. Test study on shear strength parameters of mortar[J]. Journal of Water Resources and Architectural Engineering, 2005, 3(4): 30−32.

[8] Odah, ZHANG M L, Skimayanmam. Study on load-dispersive anchorage and shear stress in surrounding soils[C]// Proceedings of International Conference on Application and Development of Rock-Soil Anchoring Technology. Liuzhou, 1997: 237−244.

[9] 高德军, 李元松. 拉力型锚杆锚固力学性能试验研究[J]. 人民长江, 2016, 47(4): 58−63.GAO Dejun, LI Yuansong. Experimental research on the mechanical properties of tensile-type anchoring[J].Yangtze River, 2016, 47(4): 58−63.

[10] 张培胜, 阴可. 拉力型锚杆锚固段传力机理的全过程分析方法[J]. 地下空间与工程学报, 2009, 5(4): 716−723.ZHANG Peisheng, YIN Ke. An analysis method of the whole working course for the force transferring mechanism in fixed segment of tensile-type anchor bar[J].Chinese Journal of Underground Space and Engineering,2009, 5(4): 716−723.

[11] 尤春安. 全长黏结式锚杆的受力分析[J]. 岩石力学与工程学报, 2000, 19(3): 339−341.YOU Chunan. Mechanical analysis on wholly grouted anchor[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(3): 339−341.

[12] 陈昌富, 汤宇, 梁冠亭. 剪切模量随深度呈指数函数增大地基中锚杆弹塑性分析[J]. 中南大学学报, 2016,47(3): 905−912.CHEN Changfu, TANG Yu, LIANG Guanting.Elastic-plastic analysis for bolts in ground with shear modulus increasing following an exponential function with depth[J]. Journal of Central South University, 2016,47(3): 905−912.

[13] 杨庆, 朱训国, 栾茂田. 全长注浆岩石锚杆双曲线模型的建立及锚固效应的参数分析[J]. 岩石力学与工程学报, 2007, 4: 692−698.YANG Qing, ZHU Xunguo, LUAN Maotian.Development of hyperbolic model for fully grouting rock bolt and parameters analysis for anchoring effect[J].Chinese Journal of Rock Mechanics and Engineering,2007, 4: 692−698.