基于一维河网非恒定流模型的河道洪水位计算研究

李志勇 ，付子刚 ，李 明

河道洪水位的设计计算对于水利工程的设计至关重要，因此，近年来，研究者在此方面做了大量工作，如王伟义等人[1]基于库尔勒城市供水二期工程水源地区域水文地质参数的分析基础进行洪水位的设计；王高英[2]通过预测预报模型对渭、洛河下游洪水位进行了相关的预测性计算；肖念婷[3]利用实例对各常用设计洪水流量计算方法进行比较分析；黄国如,芮孝芳[4]通过频率组合法对感潮河段设计洪水位进行了计算；伍成成等人[5]基于数值模拟的方式对盘锦双台子河汛期防洪水位进行了数值计算；吴劭辉等人[6]基于分形理论在姚江丈亭站进行了洪水位的分析计算，以上的研究取得了众多成果，丰富了洪水位的设计计算，但在计算速度和计算时间上，还有较大的提高余地。本文基于一维河网非恒定河流模型，用于洪水设计计算，为了方程求解，采取Preissman四点隐式差分格式离散求解流程。

1 一维河网非恒定流模型

在水位和流量未知的情况下，将一维非恒定流圣维南方程组引入，该方程组以河道漫滩与旁侧入流为基础，流量用 Q（x,t）表示，水位用 Z（x,t）表示，则一维非恒定流圣维南方程组为：

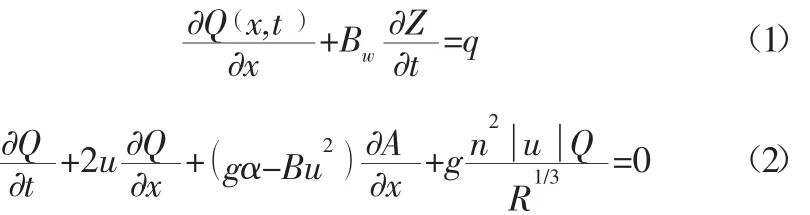
在（1）、（2）式中，坐标标度用来 x表示，单位为 m；水面宽度用Bw来表示，单位为m，这里的水面宽度不仅包括主流宽度，也包括具有调蓄作用的附件宽度，而主流断面宽度用B来表示，单位为m；时间用t来表示，单位为s；旁侧入流流量用q来表示，其单位为m3/s；主流过水断面面积用A来表示，单位为m2；另外，水力半径用R表示，糙率用表示n，重力加速度为g，单位皆为国际单位制。

（1）、（2）式为一阶双曲线型拟线性偏微分方程组，该方程组根据普通数学解析方法无法求出准确的解析解，因此需要通过近似逼近的方法进行求解，四点隐式差分格式离散方程组对于该类方程组可以求得较好的结果，即Preissman方法，因此，该文通过此方法进行求解。

2 Preissman四点隐式差分格式离散求解

2.1 求解思路

方程组的求解是Preissman四点隐式差分格式离散方程组中占用求解成本最大的环节，是占用求解时间最多的环节，而水位方程组的一种并行求解方法，可以极大地缓解求解的成本问题，可较大地缩短求解的时间，这可以成为一个高效求解方程组的思路，而在该思路的基础上，以分解型并行和递归型并行可以实现模型的编译与编程。

主程序在服务器上进行递推，若进行到求解河网方程组时，系统可以立刻实现对河网的划分，客户端可以自动接收划分之后的最终结果，接收之后，会将划分后的结果文件向各个客户端进行传递，直至客户端完全计算完毕。之后，服务器将收到最终的方程求解结果，然后进行比较以及下一步的计算。

2.2 求解流程

用如下框图表示求解流程：

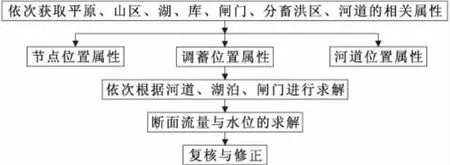
图1 求解流程框图

根据图1所示的求解流程框图，如每一行只有一个框图的则必须进行完这个框图，才可以进行下一个框图的计算，而每一行有多个框图的，如第二行，则可以同时进行，其遵循如下流程：

（1）依次获取平原、山区、湖、库、闸门、分畜洪区、河道的相关属性，其是在基于该模型的主线程的基础上，所建立的六个子线程，即平原、山区、湖、库、闸门、分畜洪区、河道的主线程。

（2）同时可以获取节点位置属性、调蓄位置属性、河道位置属性。此过程是将（1）中的六个子线程关闭，而后创建三个子线程，即节点位置属性、调蓄位置属性、河道位置属性。

（3）依次根据河道、湖泊、闸门进行求解。将（2）中创建的三个子线程关闭，然后，可以按照河道、湖泊、闸门进行求解，求解中只用到所求解位置的数据，不会影响其他的数据，如求解河道属性时，便与其他属性无关。

（4）断面流量与水位的求解。这里采用超松弛不断迭代的方式进行求解。

（5）复核与修正。由于迭代算法难免存在误差，因此，需要进行复核与修正，修正的前提是节点水位流量保持平衡，平衡之后，可不需再修正。之后进行下一周期的迭代。

2.3 求解算法效率

为了表征该求解算法的求解效率，需要用一个特定参数来进行相关度量，在计算数学里，可采用加速比进行度量，其是一个评价在一个系统里获得多大利益的一个参数，其定义为：

在（3）式中，计算器所处理数据所用得时间成本为Ts，而处理器所用的时间成本为Tp，即为p个处理器。

此外，还可通过效率比，来表征每个处理所处理数据的效率与能力，是处理器发挥能力的度量，效率比用表示Ep，有：

Ep是介于0与1之间的数，就处理器数为p而言，Ep值越接近1，即100%，则效率越高，而100%的效率是最理想型的效率。

3 实例应用

3.1 概况

石碛河为长江南京段北岸支河，发源于浦口境内西南山丘区的天井山和三岔水库上游，流经桥林街道集镇至七坝入长江，被列入《江苏省骨干河道名录》。石碛河三岔水库以下干河长度约16 km，其中由候家坝至江口段长约7.65 km，流域总汇水面积约125 km2，其中桥林镇区段以上为山丘区，总面积约107 km2。

石碛河桥林街道集镇至入江口段堤防，通过2000年的除险加固工程、2007年水利血防工程及2010～2012年南京市长江干堤防洪能力提升工程等历年建设加固治理，堤防情况较好，堤顶高程基本达标。本次桥林镇区段堤防由于两岸堤后民房密布，治理所需拆迁经费巨大，因此以往工程中并没有对该段堤防进行达标整治，堤防防洪标准不足20年一遇，堤顶高程偏低，无防汛道路。

根据现状地形、山丘区洪水流向将流域山丘区划分了10个水文分区。各水文分区见图2，各水文分区流域特征值见表1。

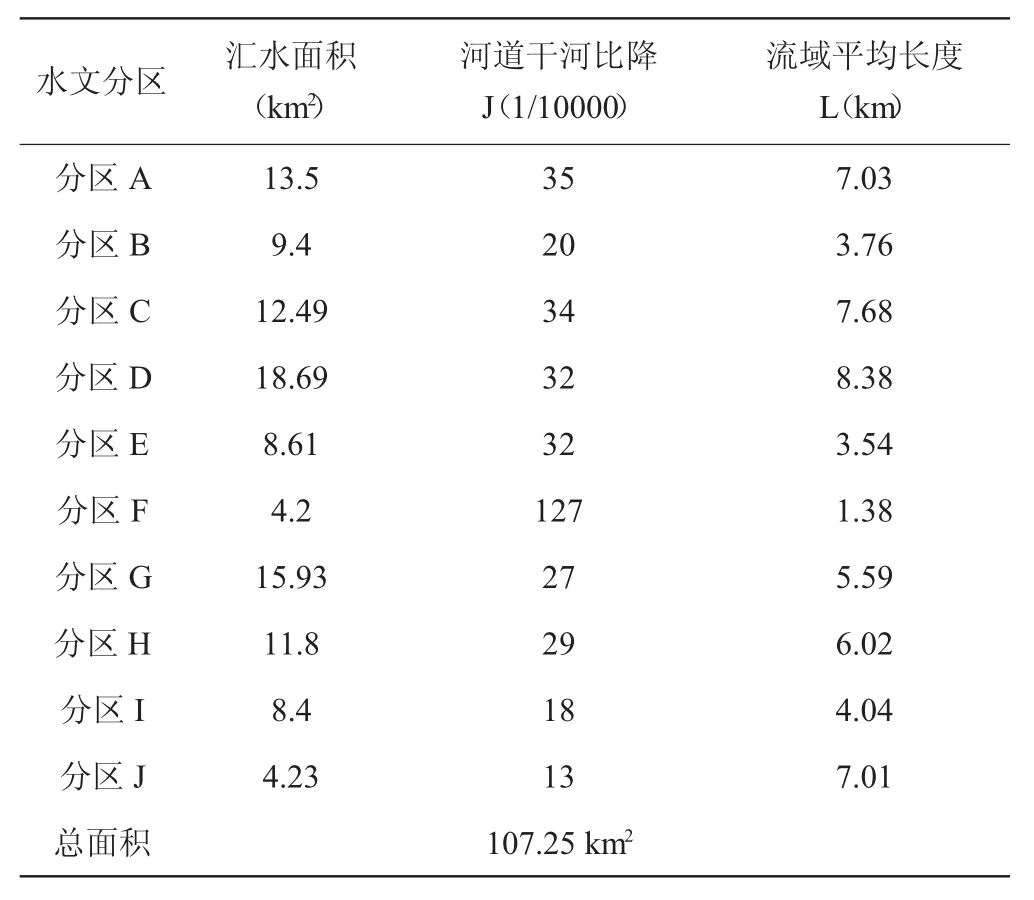
表1 各分区流域特征值表

3.2 河道防洪水位计算

将上所述的一维河网非恒定流模型通过计算机编程，建立石碛河一维河网非恒定流模型，通过模型计算水位、流量。模型按照确定的两个口门（上边界、下边界）边界条件进行控制，模拟洪季大潮上边界为流域各分区支河入流过程，下边界遭遇河口长江潮位。计算所需的洪水组合如下(1)和（2）：

（1）50年一遇防洪水位：流域50年一遇降雨遭遇河口长江“91.7”高潮位10.16m所得河道设计水位与“长流规”潮位11.03m回水取外包线；

（2）20年一遇防洪水位：流域20年一遇暴雨遭遇长江“91.7”高潮位10.16m。

最终系统算出的水位结果绘入图3中，并进行比较，其为现状20、50年一遇水位与两岸高程比较图。

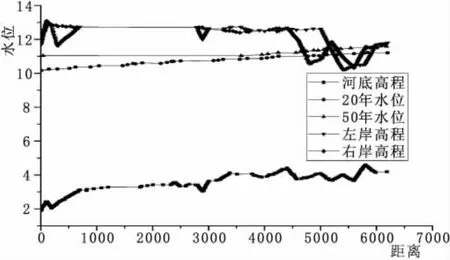
图3 现状20、50年一遇水位与两岸高程比较

由图3计算内容并采用内插法可得，石蹟河桥林镇区段堤防（K5+700～K4+560）断面设计水位为11.54～11.33m。

通过分析发现，现状条件下石碛河水利血防工程整治段（K3+000～河口）满足50年一遇防洪标准，左、右岸堤防高于50年一遇水位约1.6m以上；左、右岸堤防高于高于50年一遇防洪水位1.4m～1.5m；而堤防工程位于桥林桥林镇区段K4+200～5+800之间，除右岸K4+400～K4+800外，防洪标准不足20年一遇。

3.3 计算效果分析

系统采用两台计算机进行计算，即处理器数为2，p值为2，将系统内部的耗时数据读出，可得，计算器所处理数据所用的时间成本为342 s，而处理器所用的时间成本为183 s。

将数据带入（3）和（4）得，加速比为 1.86 s，将其除以 2，可得出效率比，经计算，效率比值为93%，由效率比可以看出，该文的系统程序运行效率较高，说明方法与配置比较合理，可供相关工程技术人员提供参考。

4 结论

（1）基于一维河网非恒定河流模型，用于洪水设计计算，为了方程求解，采取Preissman四点隐式差分格式离散求解流程，并可通过加速比和效率比对算法的效率进行校验，极大地提高了计算效率，该方法流程可为相关工程人员进行洪水设计时提供参考。

（2）将所述模型与算法流程用于石碛河的洪水位设计，所得结果为：现状条件下石碛河水利血防工程整治段满足50年一遇防洪标准，左、右岸堤防高于50年一遇水位约1.6m以上；左、右岸堤防高于高于50年一遇防洪水位1.4m～1.5 m。

[1]王伟义,杨美娥.库尔勒城市供水二期工程水源地区域水文地质参数的分析[J].甘肃水利水电技术,2014,50(07):43-46.

[2]王高英.渭、洛河下游洪水位预报模型初探[J].陕西水利,1995,(02):27.

[3]肖念婷.小流域设计洪水计算方法的探讨 [J].水科学与工程技术,2013,(05):14-16.

[4]黄国如,芮孝芳.感潮河段设计洪水位计算的频率组合法[J].水电能源科学,2003,(02):72-74.

[5]伍成成,郑西来,林国庆.盘锦双台子河汛期防洪水位的数值计算[J].水力发电,2011,37(07):12-14.

[6]吴劭辉,张彦芳,夏梦河.分形理论在姚江丈亭站洪水位分析计算中的应用[J].浙江水利科技,2003,(04):28-30.