基于GAC的局部自适应海岸线亚像元定位算法

陈飞宇，胡友彬，施恩

（国防科技大学气象海洋学院，南京 211101）

0　引言

海岸线是陆地与海洋相互交汇的部位，包括大陆海岸线和岛屿海岸线，不仅标识了沿海地区的水陆分界线，而且蕴含着丰富的环境信息，并对沿海的滩涂面积、湿地生态系统的兴衰等具有重要的指示作用。近些年来，遥感技术以其观测范围广、信息量大、获取信息快、更新周期短等优点，逐渐成为海岸线提取的重要方法和手段。

混合像元是指在传感器的瞬时视场中包含多种地物类别的像元（如图1所示），是遥感影像所固有的特征[1-2]。硬分类方法将混合像元完全归为某一种地物类型，会导致分类结果不准确。如何对遥感影像中这种广泛存在的混合像元问题进行处理已经成为定量遥感分析中最为关键的问题[3-4]。亚像元定位（Sub-Pixel Mapping，SPM），也称超分辨率制图（Super-Resolution Mapping，SRM），是目前解决混合像元问题的常用手段，其目的是确定混合像元中不同地物类型的具体空间位置，获取更高空间分辨率的地物分类图。因此，亚像元定位可以看作是一种提高遥感影像空间分辨率的技术，即将低分辨率遥感影像的混合像元分解转换成高分辨率的地物分类图。海岸线的亚像元定位是指在混合像元内部确定水、陆的空间分布，国内外学者对此做出了深入地研究，取得了丰硕的成果。张旸等[5]使用黄河三角洲海岸Landsat卫星遥感数据，基于研究区域低分辨率6波段的海陆类型软分类结果及其变差函数，以高分辨率8波段的指示变差函数为精细尺度先验信息模型，采用地统计学方法生成海陆类型发生概率模拟图像，通过等值线法提取海岸线空间分布特征。凌峰等[6]考虑到亚像元定位是一个欠定反演问题，其约束条件远远少于求解参数，采用高分辨率的数字高程模型作为海岸线亚像元定位的辅助信息，有效提高了海岸线亚像元定位的精度。Foody等[7]详细分析了对海岸线提取进行亚像元定位分析的必要性，分别通过拟合软分类的类别成员轮廓法和地统计学法进行海岸线的亚像元定位，并与硬分类方法的提取结果进行了对比。Muslim等[8]认为在同类地物光谱差异较大的遥感影像中选取全局的陆地端元和水体端元，缺乏代表性，误差较大，提出了基于局部软分类的海岸线亚像元定位技术，该方法根据光谱差异，选取若干个样本区域，再将提取的海岸线分成若干段，每段海岸线就近选取地类端元，并将该思想分别应用到两点直方图法和像元交换法中，取得了较好的效果。Muad等[9]以多幅时间序列的遥感影像为数据源，采用Hopfield神经网络方法对湖泊边界进行亚像元定位，与单幅影像相比，精度显著提高。

然而，海岸线的亚像元定位结果受地类组分误差的影响较大，采用全局端元进行光谱分解得到地类组分的亚像元定位方法并未考虑遥感影像中属于同类地物的不同像元可能存在的较大光谱差异的情况。例如，在现实生活中，陆地可能是淤泥、岩石或者植被等多种地物，反映在遥感影像上就是光谱值的多种多样，同样，海水随着温度、盐度等的变化，其反射率的值也各不相同。因此，选取全局的陆地和海水的端元，不能充分反映属于同类地物的不同像元之间存在的较大的光谱差异，从而造成混合像元分解误差，影响海岸线亚像元定位的精度。

针对上述问题，本文提出了基于GAC的局部自适应海岸线亚像元定位（Locally Adaptive Sub-Pixel Shoreline Mapping based on GAC algorithm,LA_SPSMG）算法。该算法首先采用GAC模型提取初始海岸线，然后通过数学形态学腐蚀和膨胀操作，得到需要进行亚像元定位的混合像元，最后采用局部自适应选取地物端元、融合光谱信息的亚像元定位方法提取海岸线，减缓了采用全局端元引起的光谱分解误差的影响，提高了海岸线亚像元定位的精度。

图1　纯像元与混合像元示意图

1　基于GAC的初始海岸线提取和混合像元确定

对海岸线进行亚像元定位，首先要确定需要进行亚像元定位的混合像元集合。根据水、陆的空间位置关系可知，海陆交界处的像元最有可能为混合像元。因此，本文利用GAC模型得到初始的海岸线，然后通过形态学膨胀和腐蚀等操作可得到以初始海岸线为中心的向水、陆两侧扩展一定宽度的带状区域，假设该带状区域内的像元为混合像元，这个带状区域之外的像元为纯水像元或者纯陆像元。

1.1　初始海岸线提取

测地线活动轮廓（Geodesic Active Contour,GAC）模型[10]是一种基于变分原理的图像分割方法，其主要思想是利用黎曼空间中的测地线概念，把寻找图像中的边界线问题转化为寻找一条加权弧长最小值问题，利用能量泛函，结合图像低层数据和高层信息（如目标边缘轮廓的连续性、闭合性、形状先验信息等）来完成分割。该模型具有对噪声不敏感、检测精度高等优点，所得到的光滑连续曲线可弥补目标轮廓上的噪声、间隙以及其它不规则形状，非常适合于海岸线这类具有复杂特征地物的轮廓提取。因此，本文以遥感影像为数据源，采用GAC模型得到初始的海岸线。

设γ(q):[0,1]→R2为平面参数曲线，I:[0,a]×[0,b]→R+为待检测图像，定义能量泛函

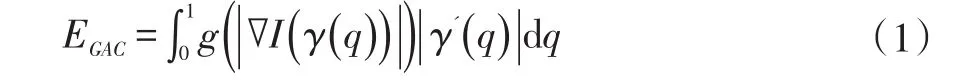
其中，g(·)为停止函数：

其中，Gσ是方差为σ的高斯核函数，因此，g为关于图像梯度强度的递减函数。

计算能量泛函式的变分，曲线演化的梯度下降流为：

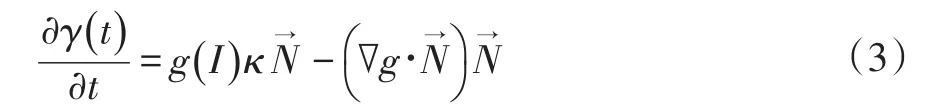
其中，κ是欧氏空间曲率，N→是单位内法向量。

利用差分法对式（3）进行离散化求解，经过若干次的迭代演化，可得到海岸线轮廓。

1.2　混合像元的确定

数学形态学的基本原理是将结构元素在图像范围内平移，同时施加交、并等基本集合运算，从而保留主要形状，删除不相干形状（如噪声、毛刺等）。设初始海岸线的二值化图像为A，模板（结构元素）为B，则A被B膨胀表示为A⊕B，得到的膨胀后的图像为：

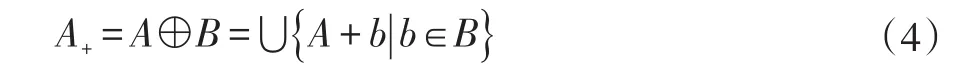
A被B腐蚀表示为 AΘB，得到的腐蚀后的图像为：

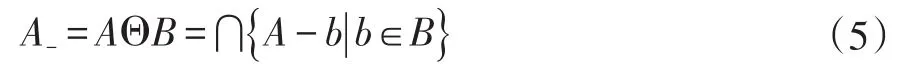
则需要进行亚像元定位的混合像元集合表示为：

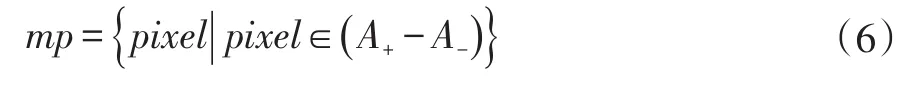
通过纯陆像元、混合像元和纯水像元三者之间的空间位置关系，可进一步得到纯水像元集合pw和纯陆像元集合pl。

如图2所示，图2（a）中的研究区域是一个小岛，提取初始海岸线后，将得到的二值化图像进行膨胀和腐蚀，中间的带状区域（图2（b））即为需要进行亚像元定位的混合像元的集合，再根据海陆之间的空间关系，易知混合像元带状区域往里的部分是纯陆像元的集合，往外的部分是纯水像元的集合，这样就得到了混合像元集合mp、纯水像元集合pw和纯陆像元集合pl。

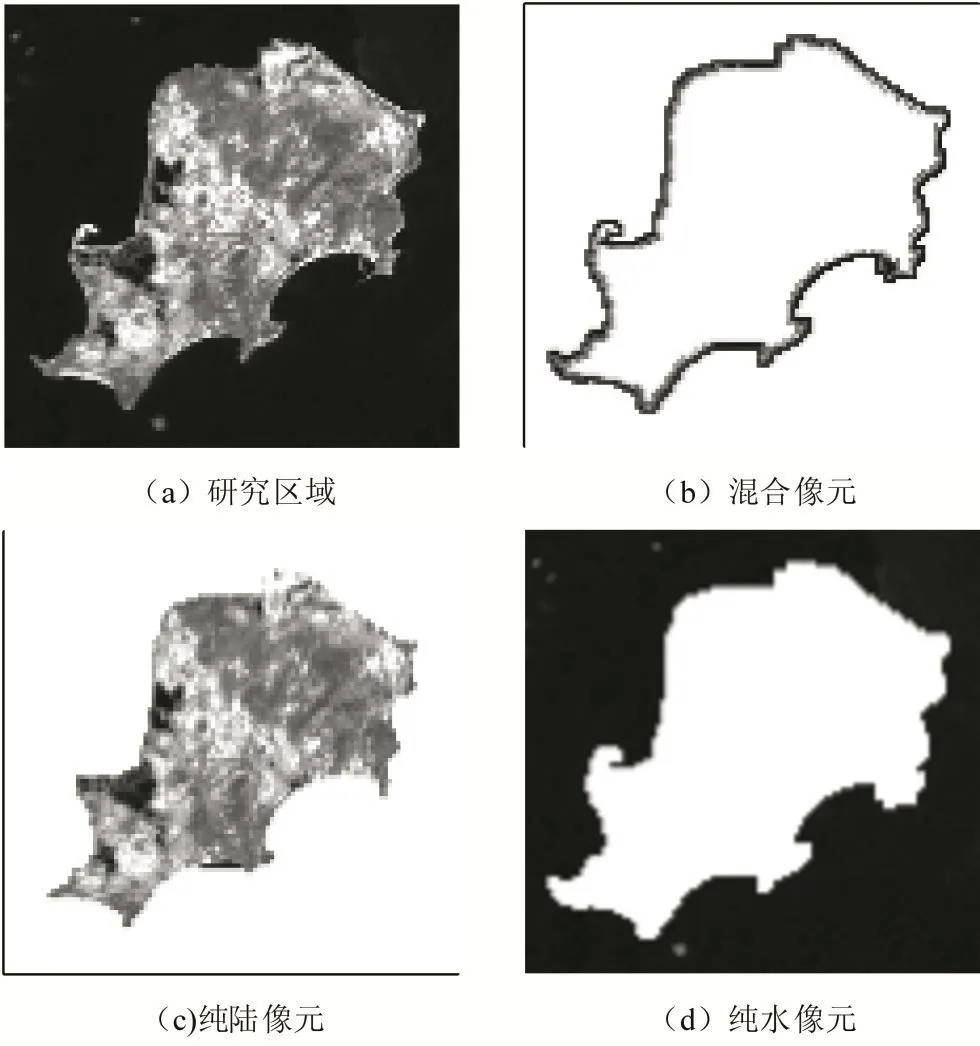
图2　混合像元集合、纯水像元集合和纯陆像元集合的确定

2　基于全局端元的亚像元定位方法

假设进行亚像元定位的低分辨率遥感影像Y共有L(L≥1)个波段，Y的每个波段图像共包括M×N个像元，放大因子为s，Y的每个像元被分割为s2个亚像元。输入数据为低分辨率遥感影像Y，输出数据为亚像元定位图像X，X包含(M×s)×(N×s)个亚像元。li(j)∈{1,…,K }代表第i个混合像元中第 j个亚像元的地物类别，其中i∈mp，1≤j≤s2，K表示地物类别数，在海岸线的亚像元定位过程中，一般取K=2，即水和陆两种地物类型。融合光谱信息的亚像元定位模型表述如下：

其中，E是求取X的能量函数，Espectral是光谱能量函数，用于通过Y对X进行光谱约束；Espatial是空间能量函数，通过空间相关性原理对X进行空间分布上的约束；β是平衡参数，用于控制光谱能量函数和空间能量函数的权重。依据最大后验概率理论，最有可能的亚像元定位结果：

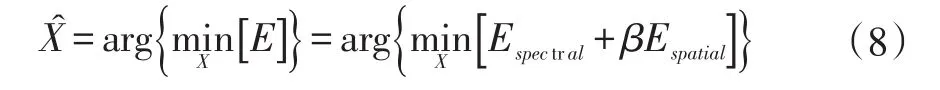
由式可知，求解X，最关键的是确定Espectral和Espatial。

2.1　光谱能量函数

光谱能量函数的主要作用是确保亚像元定位结果满足组分约束，假设低分辨率遥感影像的光谱值服从正态分布，采用最大似然估计构建光谱能量函数[11]。Ri表示低分辨率遥感影像Y的第i个混合像元的光谱向量，μk代表第k类地物的光谱向量，θi(k)代表第i个混合像元中第k类地物所占的组分，其定义如下：

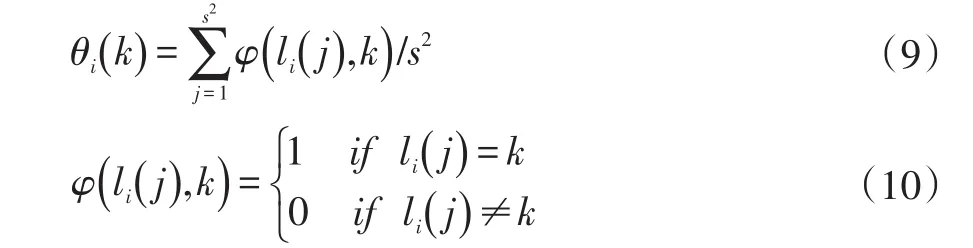
其中，1≤k≤K，li(j)∈{1,…,K }代表第i个混合像元中第 j个亚像元的地物类别。

由上述可知，第i个混合像元的光谱能量值可表达如下：

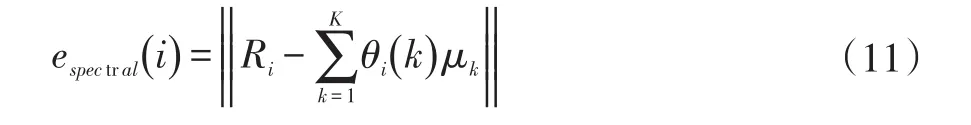
总的光谱能量值计算如下：

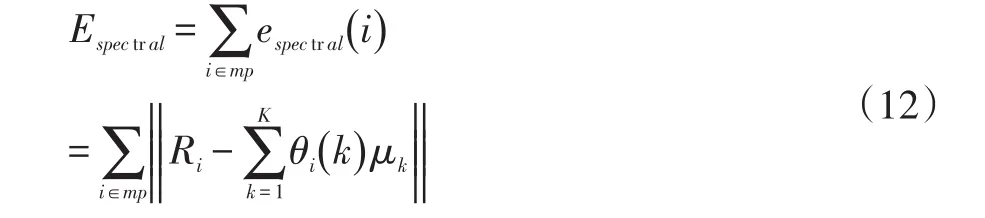
2.2　空间能量函数

空间能量函数主要是为了亚像元定位提供地物的空间分布信息。根据空间相关性原则，距离较近的亚像元和距离较远的亚像元相比，更加可能属于同一种类型，这一理论已经被广泛应用于各类亚像元定位算法中。根据这一原则，本文为待确定地物类别的亚像元选取一邻域，根据邻域中其他亚像元的地物类别来确定该亚像元的地物类别，具体模型如下：

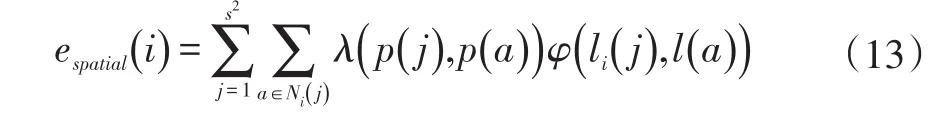
其中，espatial(i)代表第i个混合像元的空间能量值，Ni(j)表示以第i个混合像元中第 j个亚像元为中心，选取大小为w×w的方形窗口所包含的亚像元组成的邻域集合；p(·)表示亚像元的位置，λ(p(j),p(a))是各向同性空间权重函数，定义如下：

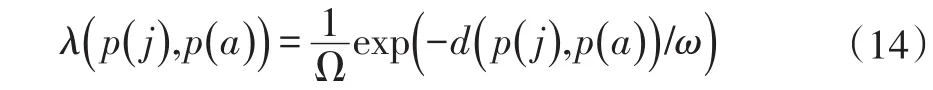
l(·)表示亚像元的地物类别，函数φ定义如下：

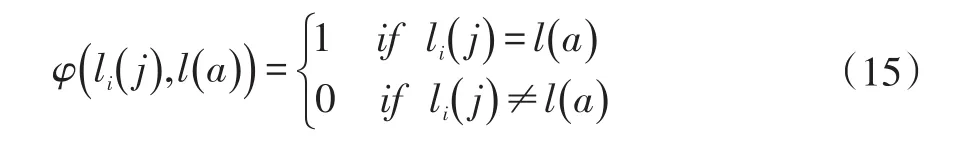
因此，总的空间能量值定义如下：

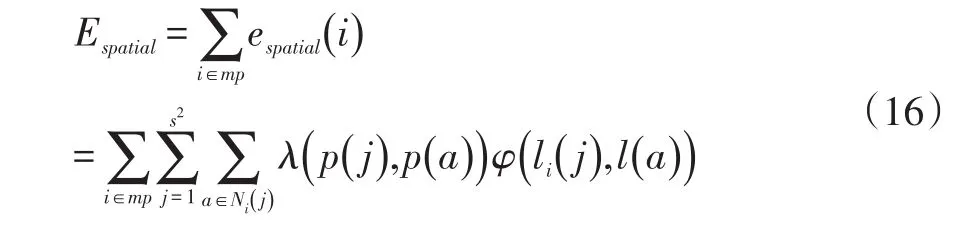
3　LA_SPSMG算法

3.1　模型的建立

由式可知，μk代表第k种地物的光谱向量，一般是通过在遥感影像上选取的若干个该类别的纯像元的光谱向量，然后求均值得到的，并且在之后对每一个像元的光谱能量计算过程中不发生改变。然而，遥感影像上同种地类不同像元的光谱值可能差异较大，选取全局的陆地和海水的端元，不能充分反映这种属于同类地物的不同像元之间的光谱差异性，会造成混合像元分解误差，进而影响海岸线亚像元定位的精度。

针对上述问题，本文提出了局部自适应选取端元的亚像元定位模型。对任意混合像元i(i∈mp) 计算其陆地或海水端元光谱的过程如下：以该混合像元为中心，选取窗口（预设定大小W×W）范围内（如图3所示）第k类地物的纯像元，如果该窗口内没有该类地物的纯像元，则增大W，扩大窗口范围，直至找到；记选取到的纯像元为 pjk，相应的光谱向量为R(pjk)，其中1≤j≤n，n为窗口内所包含的该类地物纯像元的个数，则对于混合像元i，第k类地物的端元光谱可表示为：

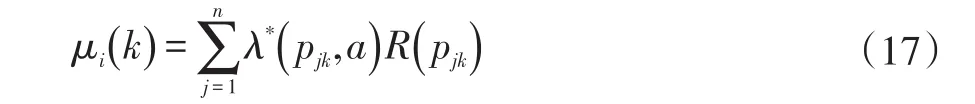
λ*()

pjk,i代表空间权重函数，其定义如下：

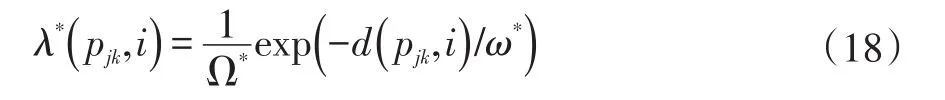
其中，Ω*为使的归一化常数，d(pjk,i)代表纯像元pjk与混合像元i之间的欧式距离，ω*为非线性参数，1≤k≤K。

将计算得到的混合像元i中第k类地物的光谱向量μi(k)带入到亚像元定位模型中，因此，LA_SPSMG模型可表示为：

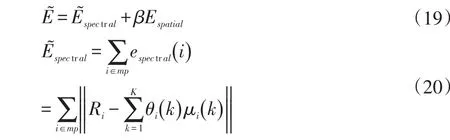
Espatial的表达式见式（16）。

3.2　模型的求解

根据式（16）、（19）和（20），最终的亚像元定位结果可计算如下：

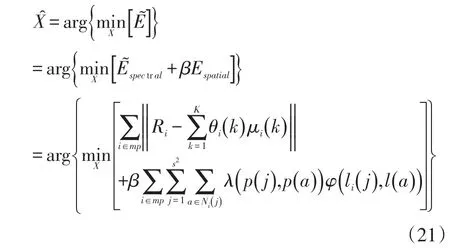
采用模拟退火算法[12]对式（21）进行求解。温度T随着迭代次数的变化如下：

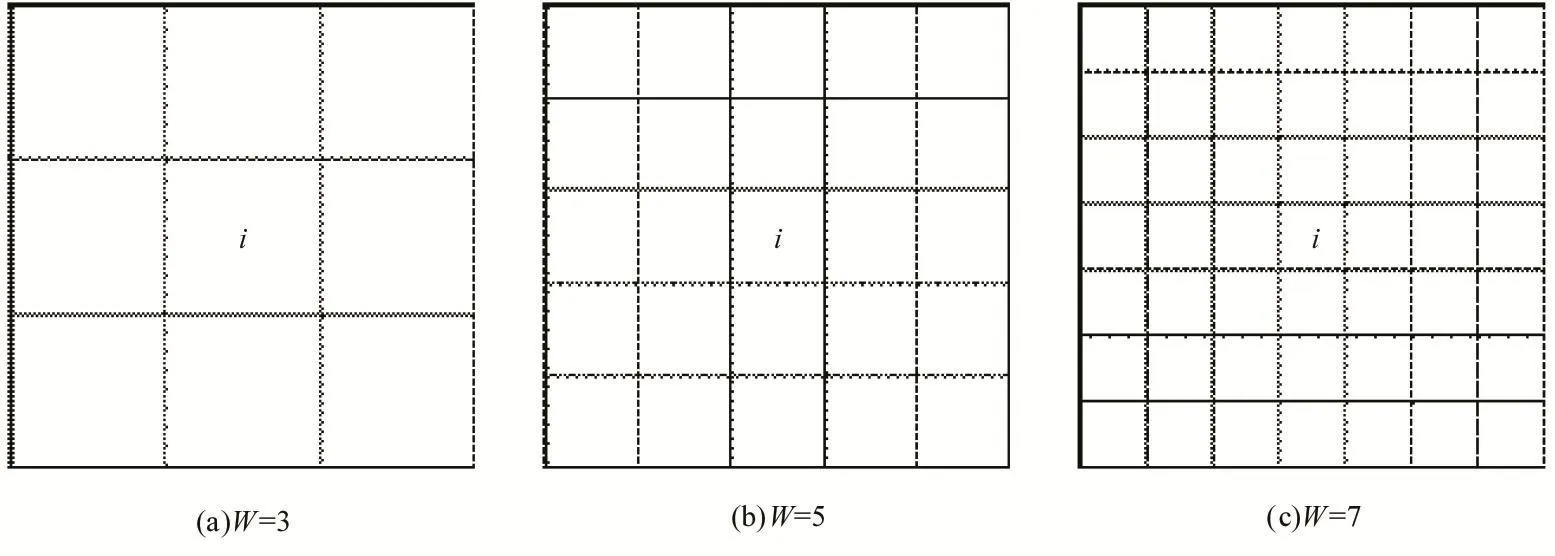
图3　邻域窗口

其中参数σ∈(0,1)控制温度下降的速率。

在初始化过程中，根据低分辨率遥感影像Y得到纯陆像元集合pl、混合像元集合mp和纯水像元集合pw，对每一个属于mp的混合像元，在高分辨率亚像元定位结果图X中对应的s×s个亚像元，随机分配地物类别。在每一次迭代过程中，如果该亚像元的类别改变使目标函数值降低，则接受这次改变；否则，根据当前的温度，以一定的概率接受这次改变。当达到最大的迭代次数后，算法运行停止。整个模型求解的算法流程如下：

算法1 LA_SPSMG算法

输入：低分辨率遥感影像Y，波段数L，地物类别数K=2，放大因子s，窗口大小w和W，非线性参数ω和ω*，平衡参数 β，初始温度T0，温度递减率σ，迭代次数t。

I）初始化：依据低分辨率遥感影像Y分别确定纯陆像元集合 pl、混合像元集合mp和纯水像元集合pw；然后依据pl、mp和 pw对高分辨率亚像元定位图X进行初始化，其中混合像元部分，在X中随机分配亚像元的地物类别。

II）生成高分辨率亚像元定位结果图

Forn=1:t

Fori=1:M×N

Ifi∈mp

a）以混合像元i为中心，构建W×W的像元窗口，分别选取低分辨率遥感影像Y中的纯陆像元和纯水像元，并计算混合像元i中第k类地物的均值向量μi(k)(1≤k≤K )；如果窗口中没有纯像元，则扩大W的值，直到找到纯像元为止。

4　实验设计与结果分析

4.1　实验设计

为了验证LA_SPSMG算法的有效性，选取两个不同研究区域分别进行海岸线的亚像元定位，并对实验结果进行定量评价。

实验1的研究区域是位于青藏高原上的一个湖泊，如图4所示。实验选用Landsat ETM+遥感影像作为实验数据，Landsat ETM+共有8个波段，其中第1～5波段以及第7波段空间分辨率为30m，第6波段空间分辨率为60m，第8波段空间分辨率为15m，多尺度的分辨率信息为实验提供了丰富的数据资源。实验所用的遥感影像成像时间为2001年9月22日，采用第6波段（空间分辨率为60m）包含目标研究区域、141×142像元大小的遥感数据作为输入的原始图像Y，放大因子s=4，最终得到的亚像元定位结果为X（空间分辨率为15m），并利用空间分辨率同样为15m的第8波段（全色波段）遥感影像作为验证数据评价定位结果的精度。实验中的其他参数如下：地物类别K=2，亚像元邻域窗口大小w=7，搜寻纯像元的窗口大小W=7，非线性参数ω=ω*=10，模拟退火初始温度T0=0.2，温度递减率σ=0.982，迭代次数t=150。实验结果如图5所示，图中黑色像素代表水，白色像素代表陆地；（a）为输入的遥感影像Y；（b）为对Y通过阈值分割得到的提取结果；（c）为对Y利用基于全局端元的亚像元定位方法得到的提取结果；（d）为空间分辨率为15m的参考影像；（e）为利用LA_SPSMG算法得到的亚像元定位结果X；（f）为从参考影像中得到的提取结果。

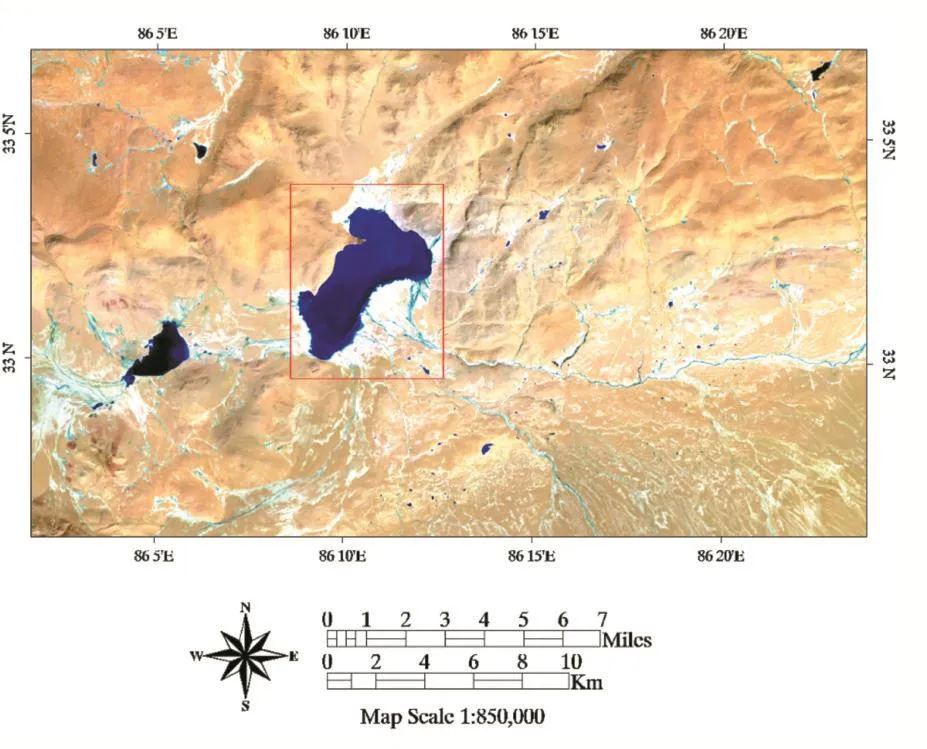
图4　实验1研究区域

实验2的研究区域是小金门岛（如图6所示），选用的Landsat ETM+遥感影像成像时间为1999年9月7日，将第3、4和5波段合成多光谱数据（空间分辨率为30m），并通过重采样将其空间分辨率降为60m，截取包含目标研究区域、105×108像元大小的多光谱数据作为输入的原始数据Y，放大因子s=4，最终得到的亚像元定位结果为X（空间分辨率为15m），并利用第8波段（全色波段，空间分辨率为15m）遥感影像作为参考数据评价定位结果的精度。实验中的其他参数设置与实验1相同。实验结果如图7所示，图中黑色像素代表水，白色像素代表陆地；（a）为输入的遥感影像Y；（b）为对Y通过阈值分割得到的提取结果；（c）为对Y利用基于全局端元的亚像元定位模型得到的提取结果；（d）为空间分辨率为15m的参考影像；（e）为利用LA_SPSMG算法得到的亚像元定位结果X；（f）为从参考影像中得到的提取结果。

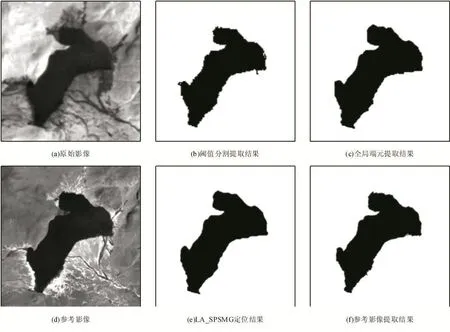
图5　实验1结果图

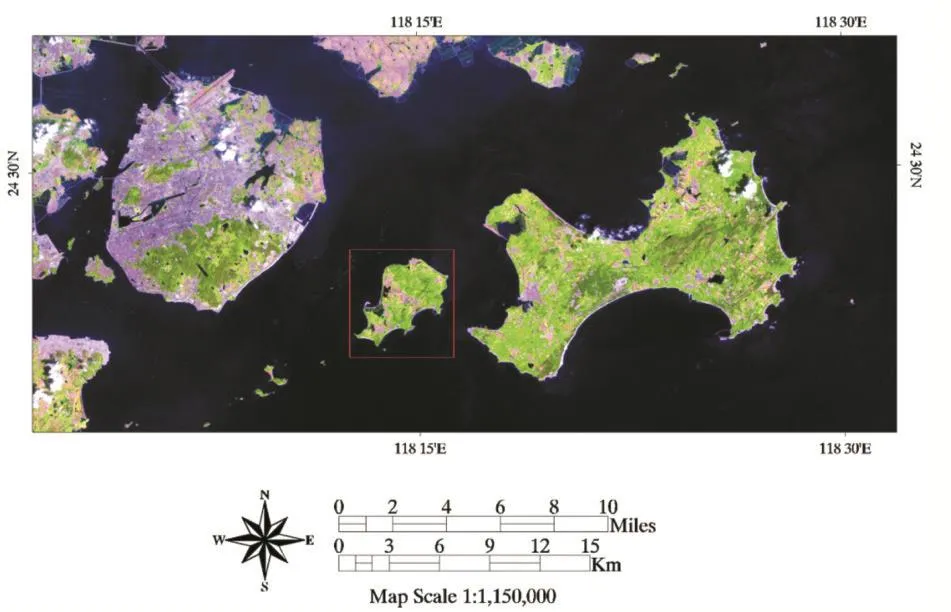
图6　实验2研究区域

5.2　结果分析

如图5所示，图（a）是空间分辨率为60m的研究区影像，在水陆边界处存在着大量的混合像元；图（b）是采用阈值分割的方法得到的水陆边界图，阈值方法将整个混合像元全部划分为水体或陆地，导致边界呈锯齿状；图（c）是采用基于全局端元的亚像元定位方法得到的提取结果；图（d）是空间分辨率为15m的参考影像，相较于原始影像，其水陆边界更加清晰；图（e）是采用LA_SPSMG算法得到的亚像元定位结果，相较于阈值分割方法的结果，水陆边界更加平滑，相较于基于全局端元的亚像元定位方法得到的提取结果，细节部分的保留更加完整；图（f）是对参考影像利用GAC模型得到的水陆边界结果。

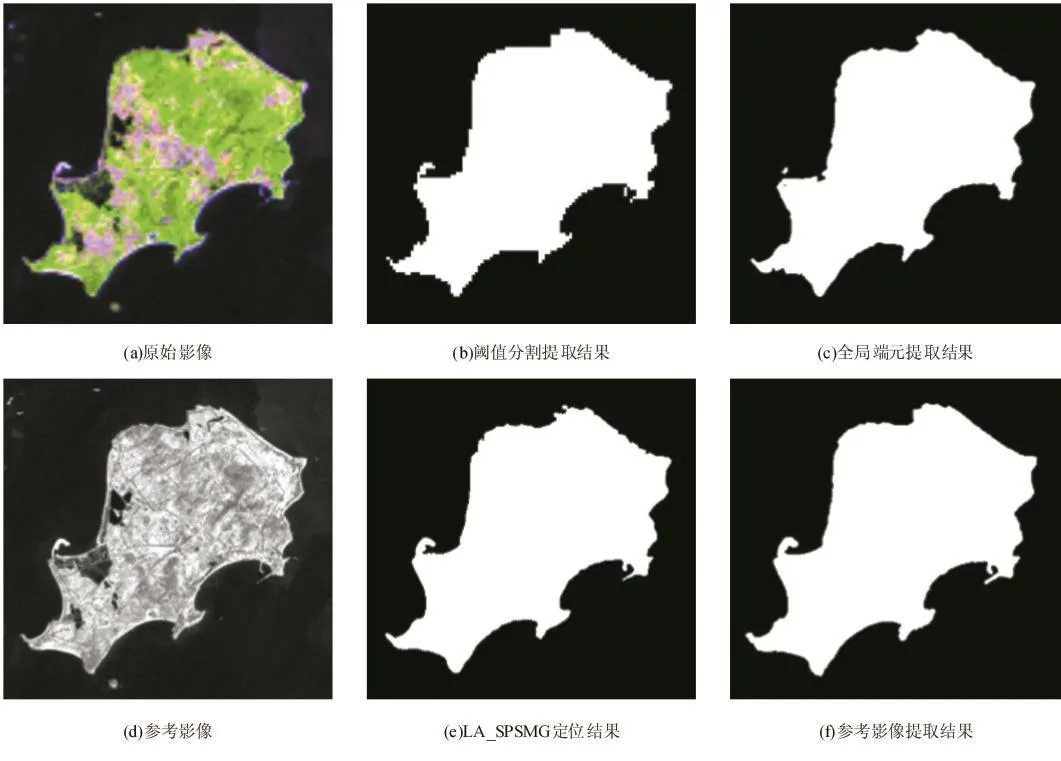
图7　实验2结果图

如图7所示，图（a）是研究区543波段合成的伪彩色图，分辨率为60m，在海水和岛屿边界处存在着大量的混合像元；图（b）是采用阈值分割的方法得到的水陆边界图，边界存在着许多毛刺，呈锯齿状；图（c）是采用基于全局端元的亚像元定位方法得到的提取结果；图（d）是分辨率为15m的参考影像，相较于原始影像，边界混合像元较少，水陆边界更清晰；图（e）是LA_SPSMG算法的亚像元定位结果，其水陆边界更加平滑，通过与参考影像的对比可知，该结果更接近于真实的水陆边界；图（f）是对参考影像利用GAC模型得到的水陆边界结果。

为了定量评价海岸线提取的精度，将利用原始影像得到的海岸线结果与高空间分辨率的参考影像对比，采用总差异（Total Disagreement，TD）、数量差异（Quantity Disagreement，QD）、分配差异（Allocation Disagreement，AD）和地物百分比均方根误差（Root Mean Square Error，RMSE）四个指标对结果进行评价。QD用于评价定位图与参考图之间由于地物百分比误差造成的差异，AD用于评价定位图与参考图之间由于地物空间匹配误差造成的差异，TD用于评价定位图与参考图之间的总体差异，其值为QD与AD之和。

QD计算如下：

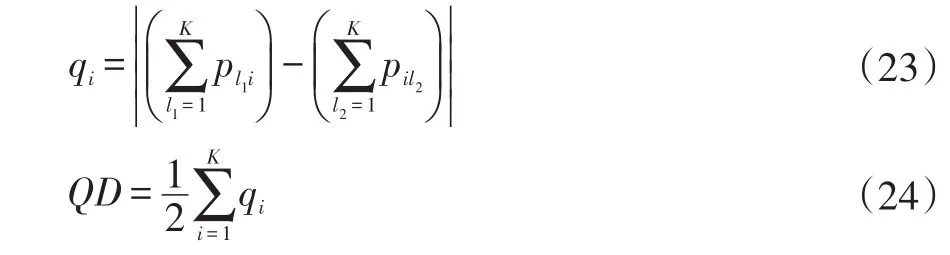
其中，pli表示在被评价图像（亚像元定位或硬分类图像）上地物类别为l，而在参考图像上地物类别为i的亚像元占总体亚像元数目的百分比。

AD的计算为：

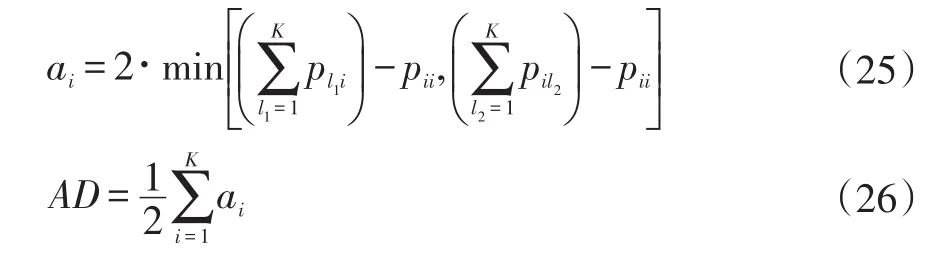
TD的计算为：

地物百分比均方根误差的计算为：

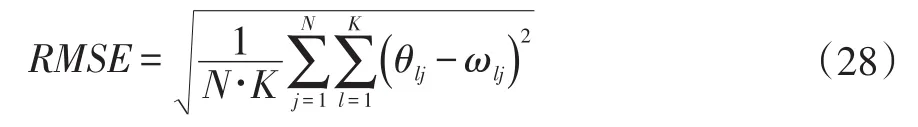
式中，N为像元总数，K为地物类别数，θlj为亚像元定位结果中第l(l∈(1,…,K))类地物在第 j(1≤j≤N)个像元中所占的百分比，ωlj为参考影像中第l(l∈(1,…,K))类地物在第 j(1≤j≤N )个像元中所占的百分比。

由表1和2可知，相比于阈值分割算法和基于全局端元的亚像元定位算法，LA_SPSMG算法无论是TD还是RMSE均最小，证明该算法在进行海岸线亚像元定位时误差更小、更有效。这主要是因为，LA_SPSMG算法局部自适应地选取端元，每一个要进行亚像元定位的混合像元都能在较小的空间范围内找到属于自己的地类端元，在一定程度上减少了全局端元带来的光谱分解误差，提高了定位精度。

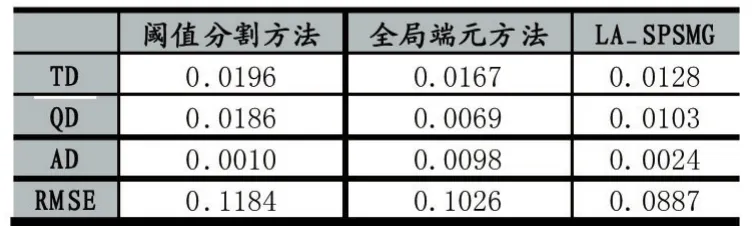
表1　实验1各算法的误差

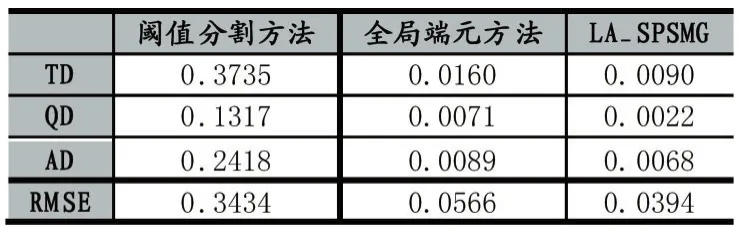
表2　实验2各算法的误差

5　结语

本文提出了基于GAC的局部自适应海岸线亚像元定位算法，该算法利用GAC模型提取初始海岸线，通过数学形态学的膨胀和腐蚀操作获取需要进行亚像元定位的混合像元集合，采用局部自适应选取端元的海岸线亚像元定位算法对得到的混合像元集合进行亚像元定位。实验表明，该算法相比于采用全局端元的亚像元定位算法定位结果误差更小、更准确。

参考文献：

[1]Li X,Ling F,Du Y,et al.A Spatial-Temporal Hopfield Neural Network Approach for Super-Resolution Land Cover Mapping with Multi-temporal Different Resolution Remotely Sensed Images[J].Isprs Journal of Photogrammetry&Remote Sensing,2014,93(7):76-87.

[2]凌峰,吴胜军,肖飞,等.遥感影像亚像元定位研究综述[J].中国图象图形学报,2011,16(8):1335-1345.

[3]Campbell J B.Introduction to Remote Sensing,3rd Edition[J].Crc Press,2002.

[4]Richards J A.Remote Sensing Digital Image Analysis:An Introduction[M].Springer Berlin Heidelberg,2006.

[5]张旸,陈沈良.结合遥感数据与地统计学方法的海岸线超分辨率制图[J].遥感学报,2010,14(1):148-164.

[6]Ling F,Xiao F,Du Y,et al.Waterline Mapping at the Subpixel Scale from Remote Sensing Imagery with High-Resolution Digital Elevation Models[J].International Journal of Remote Sensing,2008,29(6):1809-1815.

[7]Giles M.Foody,Aidy M.Muslim,Peter M.Atkinson.Super Resolution Mapping of the Waterline from Remotely Sensed Data[J].International Journal of Remote Sensing,2005,26(24):5381-5392.

[8]Aidy M.Muslim,Giles M.Foody,Peter M.Atkinson.Localized Soft Classification for Super-Resolution Mapping of the Shoreline[J].International Journal of Remote Sensing,2006,27(11):2271-2285.

[9]Muad A M,Foody G M.Super-Resolution Mapping of Lakes from Imagery with a Coarse Spatial and Fine Temporal Resolution[J].International Journal of Applied Earth Observation&Geoinformation,2012,15(1):79-91.

[10]Kass M,Witkin A,Terzopolos D.Snakes:Active Contour Models.Int.J.Comput.Vis.,1998,(1):321-331.

[11]Kasetkasem T,Arora M K,Varshney P K.Super-Resolution Land Cover Mapping Using a Markov Random Field Based Approach[J].Remote Sensing of Environment,2005,96(3–4):302-314.

[12]Tolpekin V A,Stein A.Quantification of the Effects of Land-Cover-Class Spectral Separability on the Accuracy of Markov-Random-Field-Based Superresolution Mapping[J].IEEE Transactions on Geoscience&Remote Sensing,2009,47(9):3283-3297.