基于ASIFT算法的图像特征匹配

张振宁

（四川大学计算机学院，成都 610065）

0　引言

近年来，随着信息技术的飞速发展，数字图像技术有了很大的进步，而与之关联密切的计算机视觉技术，也引起人们越来越多的关注。计算机视觉的相关研究成果已经被应用到很多领域，给人们的生活带来了极大的便利，但这离人们的最终目标还有很大差距，人们对计算机视觉技术的研究任重而道远。图像匹配技术作为计算机视觉不可或缺的重要技术之一，对其进行深入的探索与研究，将有助于推进计算机视觉的发展。

图像匹配主要衡量图像之间的相似度和一致性，是计算机视觉诸多应用的基础，例如图像检索[1]、图像拼接[2-4]、图像配准[5]、三维重建[6-8]等。如上所述的应用领域中都离不开图像匹配技术，图像匹配技术是这些技术中一个基础并且相当重要的过程。以3D打印机为例，3D打印机一般先要生成需要打印物体的模型，然后对生成的模型进行打印。其中模型可用3D Max技术生成，也可以通过拍摄实际物体各个方向的多帧图像，然后应用这些图像进行三维表面重建，生成一个实际的三维物体模型。三维表面重建过程包括图像采集、图像匹配、摄像机标定和三维位置恢复和显示。也就是说一般都是先对物体表面的各个方向进行拍摄获取多帧图像，然后对多帧图像进行匹配，进而摄像机参数标定和最后三维位置恢复和显示。其中在匹配过程中，一旦选择了不合理的图像匹配算法或者匹配算法出现问题，就会造成错误的位置匹配，从而导致后边摄像机参数计算错误，进而最后重建的三维表面和实际不一致。同样在机器人定位、车牌识别都离不开匹配，由此可见图像匹配技术的重要性。针对相同物体在不同条件下的多幅图像，由于摄像机参数、光照情况、视角变化、模糊程度等均存在差异，使得相同物体的同一区域也会表现出各种不同的形态，而图像匹配技术就是要在同一原像不同形态的像之间建立对应关系。现如今，已经产生了许多经典的图像匹配算法。2009年Jean-Michel Morel和Guoshen Yu在SIFT[9]算法的基础上提出了ASIFT[10]算法。ASIFT算法通过以一定间隔模拟相机拍摄方向的经度角（旋转角）、纬度角（倾斜角）生成两组模拟图像，最后把生成的两组模拟图像分别进行SIFT匹配。与之前的仿射不变方法相比，由于模拟了所有可能的仿射形变，ASIFT算法是一种充分的仿射不变方法。

1　ASIFT原理

在SIFT的基础上，2009年Jean-Michel Morel和Guoshen Yu提出了ASIFT算法，相比以前的算法而言，ASIFT算法是唯一的充分的仿射不变算法。

ASIFT提出经度角和维度角的概念，来描述相机的旋转角和倾斜角。ASIFT算法相比SIFT类算法具有匹配兴趣点多，能够适应非常大的视角改变等优点。

因为一个仿射变换矩阵需要六个参数，通过简单的模拟这六个参数，然后比较模拟图像是不可能实现的。一个可供替代的方法是归一化方法，已经被以往很多论文中通过不同的尝试过。一个标准的仿射变换有六个参数，由于现有的局部特征算法都能很好地适应平移不变性，我们只给其中四个参数的形式，任意一个仿射变换矩阵可以唯一的表示为：

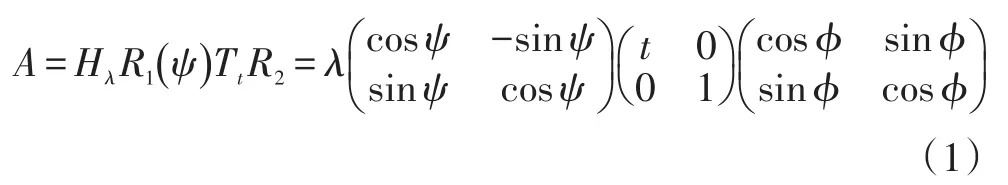
其中 λ＞0，λ代表相机的焦距，Ri是旋转，ϕ∈[0,π)，Ti是倾斜，也就是，一个对角矩阵第一个特征值是t，第二个特征值是1。

图1显示了一个仿射相机模型：ϕ和θ=sin-11 t代表观察的角度，ψ代表相机的旋转，λ对应放缩。正面拍摄的图像的参数应为λ=1，t=1,ϕ=ψ=0。

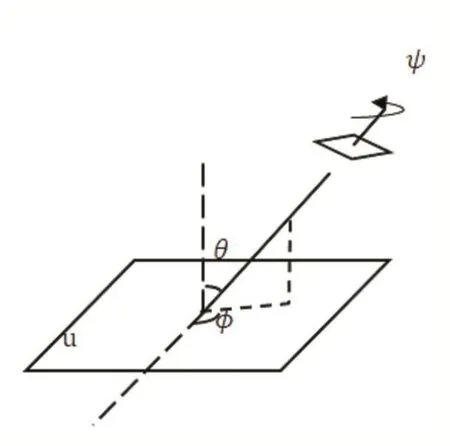
图1　相机光轴经纬度角

SIFT算法模拟了一个仿射变换矩阵的四个参数，包括相机围绕光轴的旋转，相机拍摄时候的焦距，平移和旋转。ASIFT算法模拟了仿射矩阵的两个参数，相机与图像法线的倾斜角θ和旋转角ϕ。

SIFT算法的主要思想是将模拟和归一化结合在一起。SIFT描述符归一化了平移和旋转并且通过缩放图像模拟出了所有需要查询和检测的图像。这是由于此，SIFT算法是完全尺度不变的。ASIFT精确的模拟出来所有由相机光轴方向改变所造成形变的图像，然后通过SIFT算法进行匹配这些模拟图像。换句话说，ASIFT算法模拟了一个三个参数：相机的倾斜角θ、相机的旋转角ϕ和焦距λ。尽管相机的倾斜角θ所带来的形变是不可逆的，但是可以通过在其正交方向来模拟相同数量的倾斜来补偿来模拟这一形变。与归一化方法相比，ASIFT通过这个方法模拟，实现了完全仿射不变。

2　ASIFT算法步骤

（1）针对参考图像和测试图像，首先对每帧图像在x方向进行一个标准差为c t2-1模糊.其中Lowe在SIFT论文中建议c=0.8，并证明了在c=0.8情况下只会有一个很小的走样误差。对每帧图像模拟所有因为相机光轴方向改变所造成的形变，生成模拟图像需要依赖两个参数：经度角ϕ和纬度角θ。需要同时模拟经度角ϕ和纬度角θ所照成的图像形变，纬度角θ和斜度t之间的关系为：t=|1 cosθ|(图像u(x,y)在x方向的发生斜度为t的形变，此时u(x,y)→u(tx,y))。在数字图像上，经度角ϕ是通过对图像旋转ϕ来实现，在某个方向的斜度t是通过在相对方向上进行一个t倍降采样来实现。

（2）旋转和倾斜是通过一个有限的且数量很小的经度角和纬度角来进行采样模拟实现的，采样步长尽可能的保证模拟图像可以覆盖所有不同的ϕ和θ。

（3）对参考图像和测试图像生成的一系列模拟图像，使用SIFT算法提取描述符并进行匹配。

3　经度角和纬度角的采样

（1）纬度角θ的采样时要保证其相关的斜度t满足一个几何级数序列：1,a,a2,…,an，其中a＞1.在ASIFT论文中，Morel指出a=2是一个不错的选择，此时ASIFT算法在模拟的准确度和稀疏度上都能取得很好的效果。此时n的取值可以是5或者更大，此时的相对斜度值可以达到32。

（2）经度角ϕ相对于每一个斜度t是一个等比级级数序列：0,b t,…,kb t，其中 ASIFT论文中指出b≈72°是一个不错的选择，k是一个满足kb t＜180°的最大整数。

图2显示了ASIFT算法匹配的一个直观图，其中图中的正方形A，B是参考图像和模拟图像，图中的平行四边形表示模拟图像，他们都是通过SIFT算法进行匹配的。

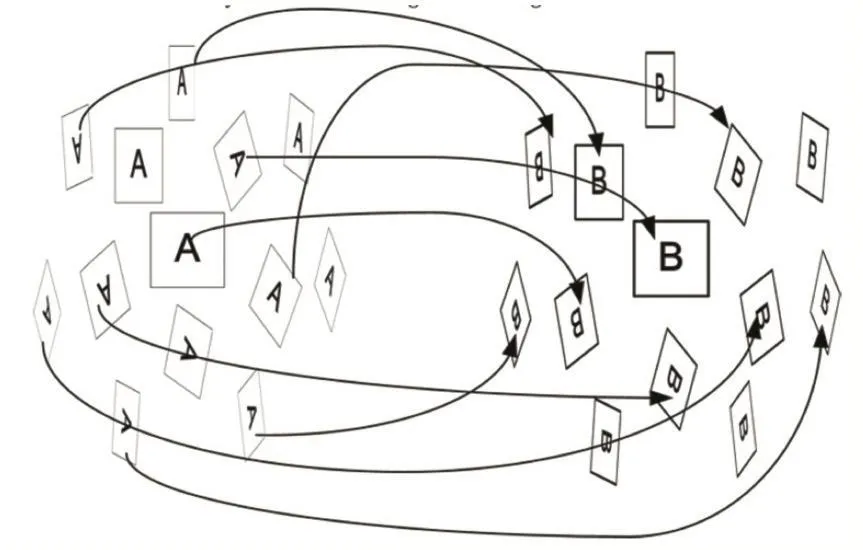
图2　ASIFT算法匹配直观图[22]

4　ASIFT采样范围和采样步骤

ASIFT采样范围：

ASIFT的采样范围由实验决定，经度角的变化范围由图1可知为0°到2π。但是从公式1我们知道，在实际中对ϕ进行采样时，范围只需要从0°到π就已经可以完全覆盖所有的仿射变换。

斜度参数t的采样范围非常关键。ASIFT假设物体表面一个很小的局部范围可以近似为一个平面结构，在确定斜度参数t时，通过用室内拍摄的图像集和室外拍摄的图像集进行多次比较分析来确定。在ASIFT论文中，其给出斜度t的一个实验得出来的上限为，其对应的最大视角值为θmax=cos-11 tmax=80°。意味着 ASIFT算法可以在=32的相对斜度下匹配两幅图像。

采样步骤：

为了使ASIFT算法对任何发生仿射形变的图像都具有仿射不变性，其斜度t和旋转角ϕ必须具有相当高的经度。其采样间隔的确定过程中需要做各种场景的大量实验。

在较大的纬度角θ下，较小的增量Δθ能使图像产生比较大的形变。对斜度t进行几何级数的采样可以满足这一要求。通常来说，采样比率Δt=tn+1tn应该与经度角ϕ是无关的。Morel在ASIFT论文中指出，斜度t的最佳采样间隔为

同样，对于经度角ϕ来说，当θ=cos-11 t增加时，在较大的纬度角θ下，图像的经度角的一个很小的增量Δϕ能够使图像发生比较大的形变。在ASIFT论文中，Morel经过大量的实验得出，Δϕ=72°t为一个比较好的选择，其中t为斜度。

图3中，按照参数θ=cos-11 t和ϕ进行采样，黑色点为采样点，左图为半球体在沿Y轴方向的透视图，右图为半球体在沿Z轴方向的透视图。

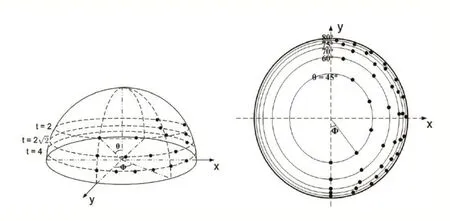
图3　　采样参数θ=cos-11 t和ϕ，黑色点为采样点

5　实验结果

实验图集选用ASIFT图像集，测试图像由图4所示的油画图像，在焦距为1倍和10倍条件下，拍摄角度在0°（正面）到80°之间生成两组图像。

图4　用做实验的图像

在焦距为1倍和10倍条件下，ASIFT匹配点的量的实验结果如表1所示：

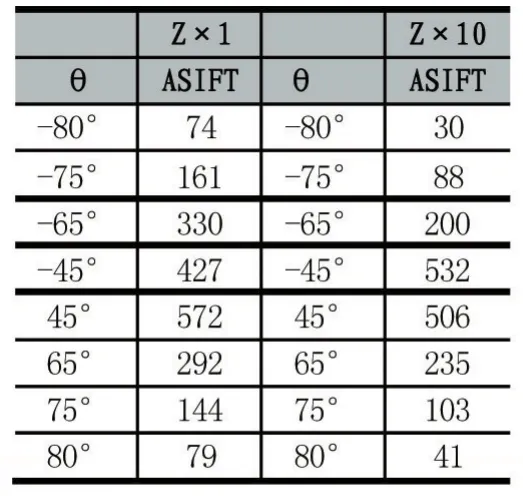
表1　

其中在1倍焦距下的，绝对倾斜θ为65°的实验效果图和在10倍焦距下，绝对倾斜为80°的实验效果图如图 5，图 6。

图5：1倍焦距下，绝对倾斜65°的实验效果图（左图）为竖直方向匹配效果（右图）为水平方向匹配效果图。

图5　

图6：10倍焦距下，绝对倾斜80°的实验效果图（左图）为竖直方向匹配效果（右图）为水平方向匹配效果图。

6　结语

根据理论描述以及实验的结果显示，ASIFT算法是一种完全仿射不变图像匹配算法。ASIFT算法不但具有旋转不变性和尺度不变性，对光照强度改变、视角变化也具有一定程度的稳定性，同时由于ASIFT算法通过以一定间隔模拟相机拍摄方向的经度角（旋转角）、纬度角（倾斜角）生成两组模拟图像，最后把生成的两组模拟图像分别进行SIFT匹配。与之前的仿射不变方法相比，由于模拟了所有可能的仿射形变，ASIFT算法是一种充分的仿射不变方法。

图6　

参考文献：

[1]K.Mikolajczyk，C.Schmid.Indexing Based on Scale Invariant Interest Points[C].Proceedings of the IEEE International Conference on Computer Vision,2001,1:525-531.

[2]M.Brown，D.Lowe.Recognising Panoramas[C].In Proceedings of the IEEEInternational Conference on Computer Vision,2003,2:1218-1225.

[3]M.Brown,S.Richard，S.Winder.Multi-Image Matching Using Multi-Scaleoriented Patches[C].In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2005,1:510-517.

[4]S.Richard.Image Alignment and Stitching:a Tutorial[J].Foundations and Trends in Computer Graphics and Vision,2006,2:101-104.

[5]J.Kybic.High-Dimional Mutual Information Estimation for Image Registration[C].IEEE 2004 International Conference on Image Processing,2004,3:1779-1782.

[6]N.Snavely,I.Simon and S.M.Seitz.Building Rome in a Day[C].In Proceedings of the IEEE International Conference on Computer Vision,2009,9(29):72-79.

[7]N.Snavely,M.Seitz Steven,S.Richard.Photo Tourism:Exploring Photocollections in 3D[J].ACM Transactions on Graphics,2006,25:835-846.

[8]Y.Furukawa，J.Ponce.Accurate,Dense,and Robust Multi-View Stereopsis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(8):1362-1376.

[9]Lowe D.Distinctive Image Features from Scale-Invariant Keypoints[J].Int.J.Comput.Vis.,2004,60(2):91-110.

[10]J.M.Morel，G.Yu.ASIFT:A New Framework for Fully Affine Invariant Image Comparison[J].SIAM Journal on Imaging Sciences,2009,2(2):438-469.