基于单目悬停相机的定轴慢旋空间非合作目标三维表面重建∗
谢朝毅 田金文 张 钧
1 引言
基于序列图像的三维表面重建是计算机视觉的一个重要的分支,在军事、工业、航天、医学等许多领域中具有广泛的应用,比如航天方面的卫星回收,军事方面的打击敌方重要军事目标,工业领域中的无人机与无人驾驶汽车,医学人体器官三维结构等。本文主要研究的是基于单目悬停相机的定轴慢旋空间非合作目标三维表面重建。下面是近年来国内外学者在三维重建领域中的研究与应用。
1992年卡内基梅隆大学的Tomasi和Kanada等[1]在假定相机正交投影的条件下通过仿射变换解算出物体三维结构和相机位姿,他们通过光流跟踪法进行特征匹配,但是这一模型的前提是目标尺寸远小于目标到相机的距离,光流法提取的特征点是稀疏点,所以重建结果整体感不强。1996年Debevec等[2]通过先验的粗略目标几何模型和相机运动参数,通过使得反投影像素误差最小化得到目标的精确三维结构,并且通过相关的纹理技术增强了视觉效果,但是先验的目标几何模型和相机运动参数是它的不足之处。2003年Yi Ma等[14]出版了一本三维重建的书籍,详细介绍了运动恢复结构算法(SFM)的各个过程;2015年Changchang Wu等[13]开发了一个名叫VisualSFM的软件系统,将SFM算法生成一个人机交互的软件,在无需相机标定的情况下,即可对无序图像进行三维重建,主要的不足之处在于耗时太长,算法的稳定性不够。2007年,SLAM(simultaneous localization and mapping)方向研究先驱A.J.Davison等[8]提出了基于EKF的实时性单目相机定位与地图构建(MonoSLAM);其最大的优点是基于视频实时三维重建,不足之处是精度不高,且是稀疏点重建。2015年Artal等[10]提出了ORB-SLAM,是现代特征点SLAM的一个高峰,提取的是ORB点特征,并提出了回环检测的环节提高了重建精度,但是ORB-SLAM是需要三个线程同时进行所以移植到嵌入式端有一定的困难,另一个不足之处就是建立的是稀疏三维点;2014年J.Engle等[10~11]提出了LSD-SLAM,标志着单目直接法在SLAM领域中的成功应用,作者有创见地提出了像素梯度与直接法的关系,以及像素梯度与极线方向在稠密重建中的角度关系,实现了半稠密化地图重建。
本文的主要工作分为两个部分:一是三维表面重建;二是重建精度分析。三维表面重建是根据运动恢复结构算法(SFM)解算相机位姿和重构自旋目标三维表面,然后根据解算的结果与真值之间进行比较,创新性地提出了边缘完整度的概念,得到三维重建算法精度评判标准。
2 方法介绍
2.1 引言
通过单目悬停相机对失稳慢旋非合作目标(主要是不可控的卫星等)拍摄的序列图像,首先解算出该目标的运动状态,然后重建出目标的三维表面,要求运动状态中旋转角度的误差不能超过0.5°,表面重建完整度达到80%以上。因为受到光照和运动噪声等因素的影响,原始序列图像首先需要进行预处理,这样得到的图像可以更精确、更多地提取到目标的特征信息用于三维重建。然后根据序列图像的先后次序提取各图像上的特征点,并进行相邻图像之间的两两匹配,通过基础矩阵得到两两之间的相对运动关系并求解出相应的三维稀疏点。接着通过使得反投影误差平方最小化迭代得到目标的稀疏点云与相机相对于目标的运动参数估计。最后通过点片面扩展模型(PMVS)获得目标的稠密点云,然后通过PCL库中泊松表面和贴纹理等技术得到目标的三维表面。本文的流程示意图如图1。
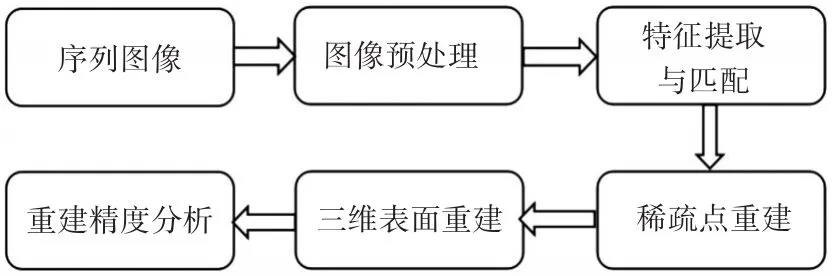
图1 三维重建过程示意图
2.2 图像预处理
图像预处理主要包括图像直方图均衡化,图像分割,图像去噪等过程,本文采用局部直方图均衡化增强图像对比度,然后进行中值滤波去噪。
2.3 图像匹配
1999年David Lowe提出 SIFT(Scale Invariant Feature Transform)算法[13]。基于SIFT提取的特征点具有尺度不变性、旋转不变性和光照条件不变性。SIFT算子首先利用尺度空间寻找极值点,并计算极值点的精确位置和所在的尺度。然后确定主方向,从而实现对尺度和旋转的不变性。最后,利用梯度方向直方图构造特征向量,从而保证光照条件不变性。当然SIFT直接匹配是需要消耗大量匹配时间的,所以选取的是k-dtree进行匹配,然后再利用周华兵博士提出的SIFT误匹配消除方法[14]可用于SIFT特征点的筛选。
2.4 相机位姿估计
目标上一特征点P在t1时刻坐标为P1,其像点坐标为(u1,v1);目标上同一特征点P在t2时刻坐标为P2,其像点坐标为(u2,v2)。O为目标旋转轴上的一定点,根据目标点绕自转轴旋转建立运动方程如下
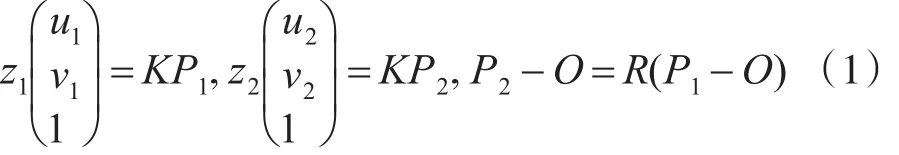
其中z1,z2分别为目标上同一特征点P在t1和t2时刻相机坐标系下的Z轴坐标值;K为摄像机的内参数矩阵;R表示自旋目标从t1时刻到t2时刻绕旋转轴的旋转变换矩阵。
根据式(1)可以求解旋转矩阵和旋转轴上的不动点O,令
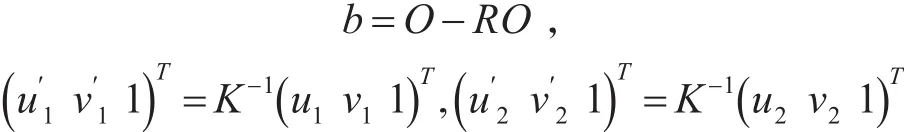
则式(1)可以转化为
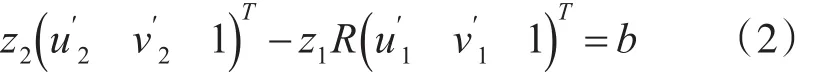
由式(2)可得:
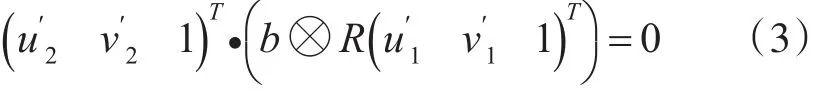
令C=b⊗R,由于目标物上提取的n个特征点,再通过图像匹配得到相应的一对对匹配点,然后可以得到如下方程:
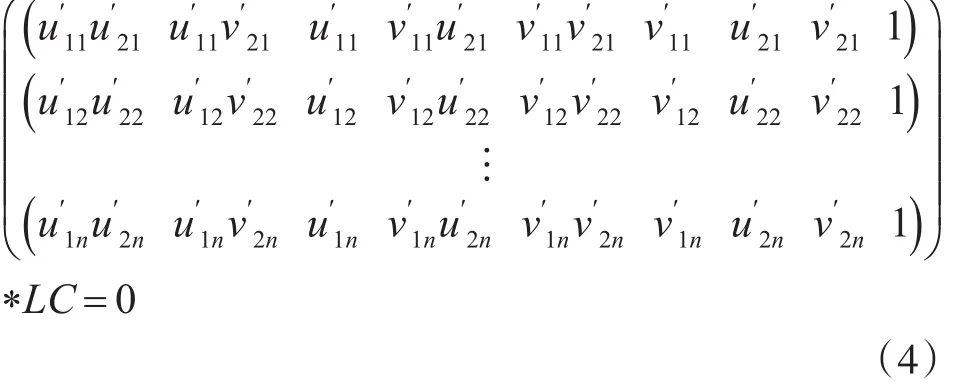
其中LC表示将矩阵C按照行优先拉伸为9×1的矩阵。
式(4)可以通过SVD分解得到相机的旋转矩阵和平移向量,但是SVD得到的结果有二组解,所以需要通过统计三维点Z轴数值大于零的个数,最大的那组解为真解。
2.5 三维稠密重建
通过2.3的步骤,我们得到了一系列不同坐标系下的三维点和相机的位姿参数,现在需要做的是将这些三维点云融合在同一个坐标系下,我们采用的是反投影误差最小化,优化相机位姿参数和三维点坐标,然后根据修改后的三维点和相机位姿通过ICP算法进行三维点融合。最小化反投影误差如下式所示:
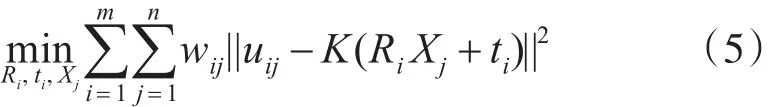
其中m,n分别表示相机的个数和三维点总个数,uij表示第 j个点在第i个相机中的像点坐标,wij表示第 j个点在第i个相机中是否有投影点,有的话为 1,否则为 0,Ri,ti,Xj分别表示第 i个相机的相对于基础坐标系(一般情况下以初始的图像对中左图相机为基础坐标系)的旋转矩阵和平移向量,第 j个三维点在基础坐标系下的坐标值。令eij=uij-K(RiXj+ti),∑-1[ ]wij即所有的wij组成的m×n的矩阵,则式(5)可以改写成:
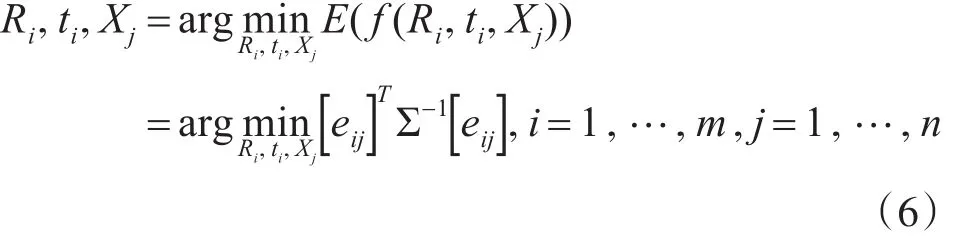
对 eij利用李群李代数的知识,即eij=uij-K exp(ξi∧)Pj,求偏导,令 P′=(RiXj+ti),得到如下两个等式:
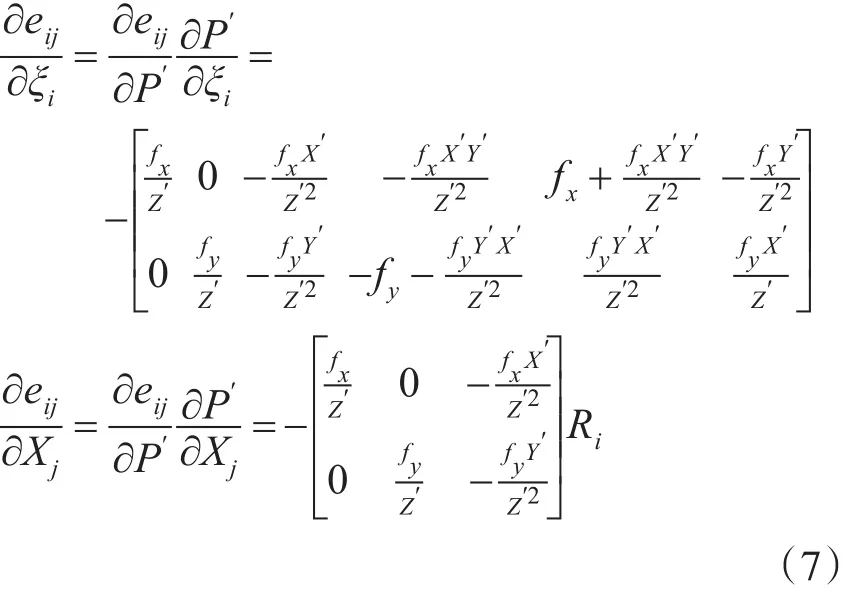
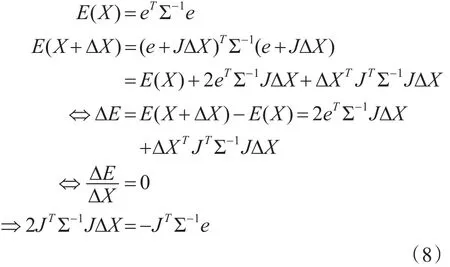
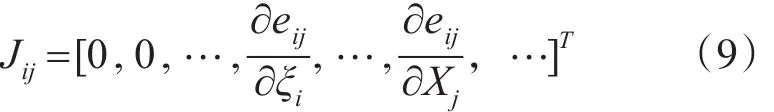
然后这个迭代问题可以通过LM算法或者高斯牛顿法等迭代优化算法求解。
3 实验结果及分析
本文通过第2章中的五个步骤得到的最终结果如图2~3。

图2 密集重建三维点云图

图3 密集重建后泊松表面三维重建图
通过上述两图可以看出,该目标的三维表面可以说重建得非常好,不管是主体框架还是纹理等特征都与真实的物体相差不多。下面是对重建的结果进行定量分析的过程和结果。
3.1 位姿精度分析
自转即空间中一点P绕着空间中任意一条转轴A旋转θ变成点P′。根据自旋理论,构建旋转矩阵如下:
最终可得旋转矩阵与旋转角度的关系:1+2cosθ=tr(G)。
统计连续的前31张图像,总共旋转的角度为55°,可以知道相邻两帧图像之间的旋转角度实际值为1.83°。表1是所有参与解算的相机旋转角度解算的结果。
3.2 表面重建精度分析
根据图像所给参数,图像的尺寸大小为2592×1944(实际图像为中心对称裁剪,实际大小为1793×921),相机焦距为25mm,像元尺寸为2.2μm,相机到旋转中心的距离为10.5m(理论上此时电池板应该平行于成像面)一个像元对应一个像素,因此一个像元对应的物体尺寸即为一个像素所表示的物理尺寸。根据三角关系。则一个像素所代表的物理尺寸为:D=d(f+L)f,代入上述数值,可计算出:D=0.00092422m。
假设点P1重建后的点为点P1′,点P2重建后对应的点为点P2′。首先统计原始图像上直线P1P2上的所有像素点数sum1,然后统计重建点云图中直线P1′P2′上的所有像素点数sum2。图像上分辨率为 N m/像素。则重建前后像素点差为sum=sum2-sum1,重建前后的直线长度相差距离为:dis=sum×N,直线上每一像素点引起的距离误差为:AveDis=dis/sum1;若重建后,两直线上的像素点数相同,那么重建后像素点数相差sum=0.5。则通过计算得到三个方向上的重建精度:水平向:0.000055m;竖直向:0.00075m;距离向:0.000055m。
3.3 边缘完整度分析
边缘完整度是指重建后的边缘上的点个数占实际图像中边缘上的像素总个数的百分比,我们通过Canny算法获取图像边缘,然后统计某个矩形区域内目标边缘点的像素个数,得到1089个边缘点,而泊松表面重建后的图Canny边缘检测在相同矩形区域的边缘点个数为876,所以得到边缘完整度为80.44%。
4 结语
本文主要介绍了基于视觉的三维重建算法研究与评估。包括空间目标图像分割与图像增强的图像预处理方法,介绍了稳定的点特征提取与匹配跟踪技术——SIFT和相应的误匹配消除方法,最后得到了基于单目悬停相机的定轴慢旋目标三维深度解算及表面重建结果,并对三维表面重建的精度进行了评估。
[1]Carlo Tomasi,Takeo Kanade.Shape and motion from im⁃age streams under orthography:a factorization method[J].International Journal of Computer Vision.1992,9(2):137-154.
[2]Y.Gao,A.L.Yuille.Exploiting Symmetry and/or Manhattan Properties for 3D Object Structure Estimation from Single and Multiple Images[C]//In CVPR,2017:724-731.
[3]P.E.Debevec,C.J.Taylor,and J.Malik.Modeling and ren⁃dering architecture from photographs:A hybrid geometry⁃and image-based approach[C]//In SIGGRAPH96,Au⁃gust 1996:11-20.
[4]Y.Gao and A.L.Yuille.Symmetry non-rigid structure from motion for category-specific object structure estimation[J].In ECCV,2016,26(5):25-45.
[5]Olivier Faugeras,Luc Robert.3-D Reconstruction of Ur⁃ban Scenes from Image Sequences[J].Computer Vision and Image Understanding.1998,69(3):292-309.
[6]M.Pollefeys,D.Nister.Detailed Real-Time Urban 3D Re⁃construction from Video[J].International Journal of Com⁃puter Vision.2008,78(2):143-167.
[7]S.Vallerand.system withpositions.M.Kanbara,N.Yokoya.Binocular vision-based augmented realityan increased reg⁃istration depth using dynamic correction of feature Virtual Reality[C]//2003.Proceedings.IEEE,2003,271-272.
[8]A.Davison,I.Reid,N.Molton.Monoslam:Real-time sin⁃gle camera SLAM[J].IEEE Transactions on Pattern Anal⁃ysis and Machine Intelligence.2007,29(6):1052-1067.
[9] A.Krull,E.Brachmann,S.Nowozin.PoseAgent: Bud⁃get-Constrained 6D Object Pose Estimation via Reinforce⁃ment Learning[J].arXiv preprint arXiv:1612.03779,pag⁃es 1-9,2017.
[10]R.Mur-Artal,J.Montiel,and J.D.Tardos,Orb-slam:a versatile and accurate monocular slam system[J].IEEE Transactions on Robotics, 2017 ,31(5):1147-1163.
[11] J.Engel, T.Schöps, and D.Cremers,Lsd-slam:Large-scale direct monocular slam[M].Springer Interna⁃tional Publishing,2014,8690:834-849.
[12]J.Engel,J.Sturm,and D.Cremers,Semi-dense visual odometry for a monocular camera[C]//in Proceedings of the IEEE International Conference on Computer Vision,2013:1449-1456.
[13]Enliang Zheng,Changchang Wu,Structure from Motion using Structure-less Resection[C]//IEEE International Conference on Computer Vision ,2015:2075-2083.
[14]Yi Ma,Stefano Soatto.An Invitation to 3-D Vision From Images to Geometric Models[J].SpringerVer⁃lag,2003,19(108):415-416.
[15]R.Hartley and A.Zisserman,Multiple View Geometry in Computer Vision[J].Kybernetes,2003 ,30(9/10):1865-1872.
[16]D.Lowe.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60:91-110.

