基于模型预测控制的开关电感准Z源逆变器研究
毛人杰 李 媛
(四川大学电气信息学院,成都 610065)
自2003年Z源逆变器(Z-source inverter, ZSI)被提出以来[1],ZSI已经成为了最具前景的电力电子变流器之一。ZSI利用直通状态来实现升压的目的,在UPS系统应用中获得广泛关注[2]。与传统的电力电子逆变器相比,ZSI具有以下优点:①能够实现单级升降压;②无需死区时间,能够消除传统逆变器死区时间带来的输出畸变;③直通状态下,同桥臂的开关管能同时导通,增加了逆变器的抗干扰能力;④元件数量较少,因此降低了系统的成本、体积,提高了系统的整体效率。然而,ZSI的升压能力仍然较差。为了解决Z源逆变器升压能力较差的缺点,文献[3-7]提出了4种不同的拓扑结构有效地解决了Z源逆变器升压能力不足的缺点。开关电感型准 Z源逆变器(switched-inductor quasi Z-source inverter, SL-qZSI)是2011年提出的一种新型的逆变器[8],以其优良的性能得到了广泛的应用。与传统的 Z源逆变器相比,SL-qZSI具有以下优点:①与ZSI和qZSI相比,在直通占空比D相同的情况下,SL-qZSI有着更高的电压增益;②输入端电流连续;③流过电感和二极管的电流应力较低,电容两端的电压应力较低。
与此同时,对Z源逆变器控制方法的研究也取得了巨大的进展。文献[9]提出了直流侧电压的直接控制方法。文献[10]提出了直流侧电压的间接控制。此外,一些学者提出了对电容电压的控制[11-12]。上述控制方法大多是通过PID控制,模糊控制,神经网络控制以及滑模控制等来实现的。
模型预测控制(MPC)从20世纪70年代问世以来,已经从最初在工业过程中应用的启发式控制算法发展成为一个具有丰富理论和实践内容的新的学科分支[13]。MPC针对的是有优化需求的控制问题,40多年来MPC在复杂工业过程中所取得的巨大成就,已充分显现出其处理复杂约束优化控制问题的巨大潜力。进入21世纪以来,随着科学技术的进步和人类社会的不断发展,人们对控制提出了更高的要求,不再满足于传统的镇定设计,而希望控制系统能通过优化获得更好的性能。与传统控制方法相比,模型预测控制(MPC)是一种简单而又有效的控制方法。MPC不需要额外的调制方法和控制内环。而且,通过MPC能同时控制不同的变量。此外,模型预测控制具有动态响应快和鲁棒性强的特点,已被应用于三相光伏并网逆变器的高性能控制等场合[14]。
1 开关电感准Z源逆变器及其工作原理
开关电感准Z源逆变器的主电路拓扑如图1所示。它由 3个电感(L1、L2和 L3),两个电容(C1和 C2)以及 4个二极管组成(Din、D1、D2和 D3)组成。由 L2、L3、D1、D2和 D3这 5个元件所组成的电路是一个开关电感单元。

图1 基于模型预测控制的开关电感准Z源逆变器
在输出侧,通过微分方程来表示输出电流:
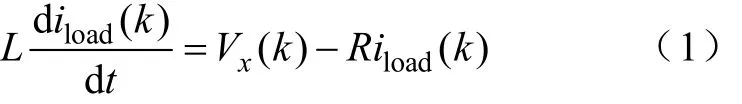
用后退欧拉公式将上式化简,由式(1)得

式中,Vx表示逆变器的输出电压,当逆变器的开关状态发生变化时,Vx的数值也会发生变化,Vx在不同开关状态下的数值见表1,Ts为采样时间,R和L分别表示负载的电阻和电感,iload为负载电流。

表1 Vx在不同开关状态下的数值
与传统的 ZSI类似,SL-qZSI也分为非直通状态和直通状态。
1.1 非直通状态
图2为SL-qZSI在非直通状态下的等效电路图。在非直通状态下,Din和D1导通,而D2和D3关断。L2和L3串联,电容C1和C2充电,而电感L1、L2、L3从直流侧向主电路转换能量。通过微分方程来表示电感电流IL1(k)和电容电压VC1(k)
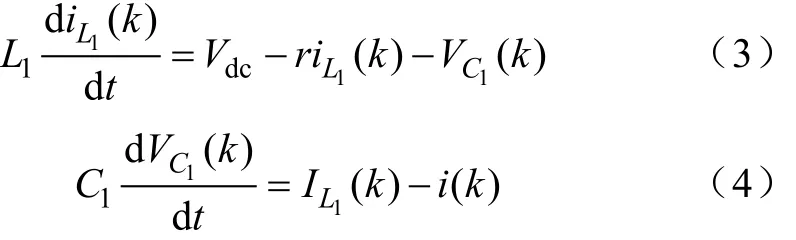
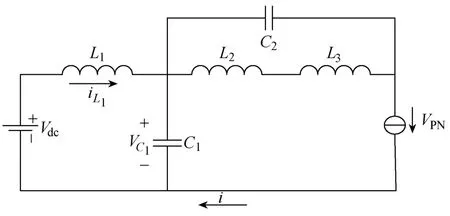
图2 SL-qZSI在非直通状态下的等效电路
同理,应用后退欧拉公式,有

式中,r为电源内阻。
1.2 直通状态
图3为SL-qZSI在直通状态下的等效电路图。在直通状态下,逆变器一侧被短路。Din和D1关断,而 D2和 D3导通,L2和 L3并联。电感 L1、L2和 L3储存能量,而电容 C1和 C2放电。通过微分方程来表示电感电流IL1(k)和电容电压VC1(k)
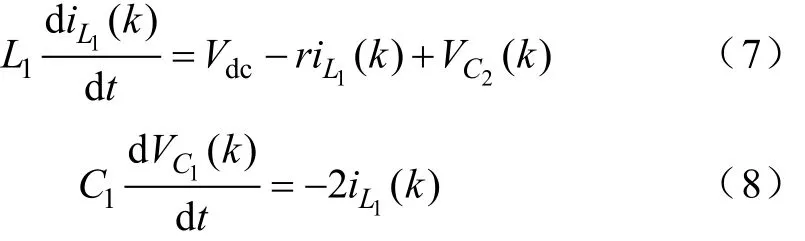
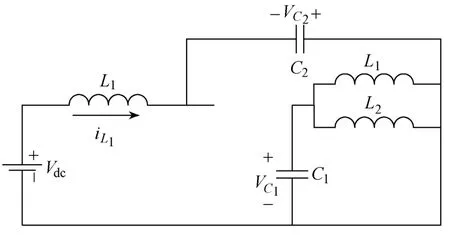
图3 SL-qZSI在直通状态下的等效电路
同理,应用后退欧拉公式,有

式中,r为电源内阻。
2 模型预测控制及其原理
模型预测控制的主要目的是通过离散化模型来预测系统控制变量未来的行为。算法首先要测量控制变量当前的数值。通过所建立的数学模型预测控制变量在下一时刻的数值。然后将所有的预测值与参考值相比,比较所有可能的方案,取最接近的一个为最优方案。其控制原理如图4所示。图中,xref表示参考信号,x为系统中的控制变量;P1, P2,…, Pn代表不同的控制方案;Xp1(k+1), Xp2(k+1), …, Xpn(k+1)各方案在下一时刻的预测值。

图4 模型预测控制原理图
模型预测控制首先利用系统在 t=tk时控制变量的值 xk预测出下一时刻 t=tk+1时控制变量的值。不同控制方案的预测值不同,在其中选取最接近参考值的预测值,并取对应的控制方案作为系统在(tk,tk+1)时间段内的控制方案。以后时间段内系统的控制方案的选取与上述方法类似[15]。
模型预测控制不仅应用在单个控制变量的系统中,在多控制变量的系统,MPC也得到了广泛的应用。这时,需要选择变量的权重因子并搭建相应的损失函数,通过比较损失函数的大小来确定控制方案。通常,取损失函数最小的为控制方案。在本文中选取VC1、iL1、iload为控制变量。定义如下的损失函数:
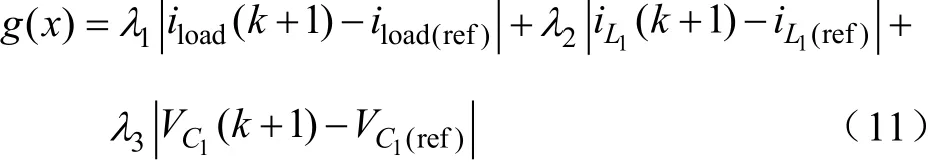
式中,iload(ref)和iload(k+1)分别表示负载电流的参考值和预测值;VC1(ref)和 VC1(k+1)分别表示电容 C1的参考值和预测值;iL1(ref)和 iL1(k+1)分别表示电感 L1的参考值和预测值,iL1(ref)基于 iload(ref)确定。λ1、λ2、λ3分别表示负载电流,电感电流和电容电压的权重因子。权重因子反应了控制变量在损失函数里的重要性。
本文模型预测控制框图如图5所示。首先,通过上文推导的式(2),式(5)、式(9)和式(6)、式(10)得出iload,iL1和VC1在5个不同开关状态下的预测值。通过所建立的损失函数式(11),得出损失函数在5个不同开关状态下的数值。在比较它们的数值之后,选择最小值所对应的开关状态作为下一个开关状态。
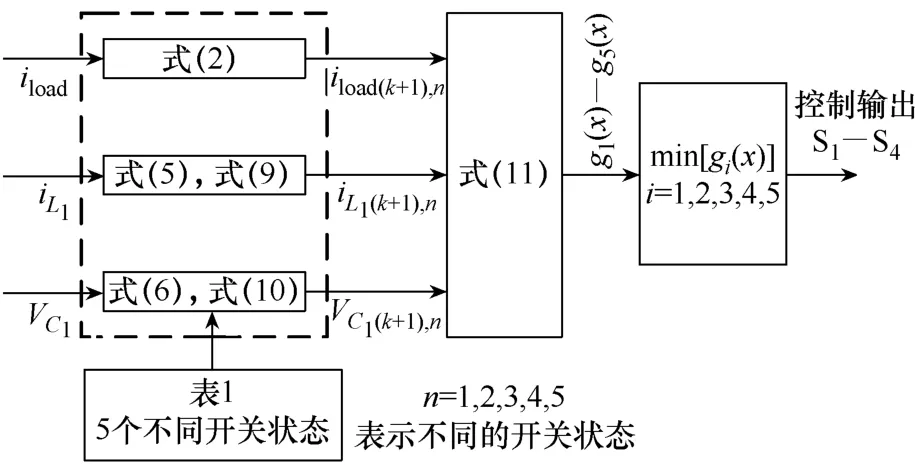
图5 SL-qZSI模型预测控制系统框图
3 仿真分析
为验证所研究的MPC的有效性和可实施性,对基于MPC的SL-qZSI在Matlab平台进行仿真研究。具体仿真参数如下:
1)L1=L2=L3=1mH,C1=C2=2000μF。
2)滤波器:Lf=4mH,Cf=12μF。
3)开关频率:f=10kHz。
4)负载:R=5.6Ω,L=0.5mH。
5)电源:Vdc=60V,r=4Ω。
6)权重因子:12.5λ=,21.2λ=,31λ=。
负载参考电流在t=0.5s时从3.5A跳变到4.2A。图6所示的是在负载参考电流跳变过程中电容电压VC1的实际波形及参考值。由仿真波形得知,尽管负载的功率发生变化,但是电容电压VC1在40V附近,能很好地跟踪参考值。这就表明MPC对于SL-qZSI中电容电压具有良好的控制作用。图7表示的是电感电流的参考值和实际值。仿真结果表明,电感电流能较好的跟踪给定的参考值。这就表明MPC对于电感电流有良好的控制作用。图8所示的负载电流也能很好的跟踪其参考值。这就表明 MPC对于SL-qZSI负载端电流有较好的控制作用。

图6 电容电压VC1的波形

图7 电感电流IL1的波形
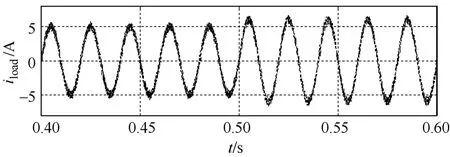
图8 负载电流iload的波形
4 结论
本文研究开关电感型准Z源逆变器的模型预测控制(MPC)方法。首先基于开关电感型准Z源逆变器工作原理建立预测模型,通过所建立的数学模型预测电容电压、电感电流和负载电流下一时刻的数值。基于多变量控制目标定义损失函数,通过损失函数的值来确定下一控制时刻的开关状态。MPC能够精确地跟踪控制变量的参考值,并快速达到稳态。此外,与传统的PID控制方法相比,其控制原理也较为简单。本文中,通过MPC能精确地控制电感电流、电容电压和负载电流。仿真结果验证了所提出方法的有效性。
[1] Peng F Z. Z-source inverter[J]. IEEE Trans. on Industry Applications, 2003, 39(2): 504-510.
[2] 王剑, 孙松松, 王传辉, 等. 基于Z源网络的UPS逆变器的研究[J]. 电气技术, 2016, 17(7): 31-35.
[3] 蔡春伟, 曲延滨, 盛况. 增强型Z源逆变器[J]. 中国电机工程学报, 2011, 31(Z1): 259-266.
[4] 侯世英, 黄哲, 肖旭, 等. 改进型Z源并网逆变器[J].电机与控制学报, 2012, 16(12): 47-53.
[5] 周玉斐, 黄文新, 赵健伍, 等. 一种高升压比的Z源逆变器[J]. 电工技术学报, 2013, 28(9): 239-246.
[6] 周玉斐, 黄文新, 赵健伍, 等. 开关耦合电感准Z源逆变器[J]. 电工技术学报, 2014, 29(6): 31-39.
[7] 赵健伍, 黄文新, 周玉斐, 等. 带抽头电感的准Z源逆变器建模与特性分析[J]. 电工技术学报, 2014,29(6): 7-16.
[8] M K Nguyen Y C, Cho G B. Switched inductor quasi-Z source inverter[J]. IEEE Transactions on Power Electronics, 2011, 26(11): 3183-3191.
[9] X Ding Z Q, Peng F. A direct peak DC-link boost voltage control strategy in Z-Source inverter[C]//APEC 07-Twenty-Second Annual IEEE Applied Power Electronics Conference and Exposition. Anaheim, CA,USA, 2007: 648-653.
[10] Tang Yu, Xie Shaojun, Zhang Chaohua. Feed-forward plus feedback control of the improved Z-source inverter[J]. 2009IEEE Energy Conversion Congress and Exposition, San Jose, CA, 2009: 783-788.
[11] Rostami H, Khaburi D A. Neural networks controlling for both the DC boost and AC output voltage of Z-source inverter[J]. 20101st Power Electronic &Drive Systems & Technologies Conference (PEDSTC),Tehran, Iran, 2010: 135-140.
[12] Shen M, Tang Q, Peng F Z. Modeling and Controller Design of the Z-Source Inverter with Inductive Load[C]//2007IEEE Power Electronics Specialists Conference, Orlando, FL, 2007: 1804-1809.
[13] 陈宁宁, 宋子豪, 汪泽州. 模型预测控制在光伏并网逆变器中的应用[J]. 电气技术, 2017, 18(4): 79-83.
[14] Qin S J, Badgwell T A. A survey of industrial model predictive control technology[J]. Control Engineering Practice, 2003, 11(7): 733-764.
[15] W Mo PC F. Model predictive control for Z-source power converter[C]//8th International Conference on Power Electronics-ECCE Asia, 2011: 3022-3028.

