机床丝杠热误差的测量与补偿研究*
刘宏伟 陈吉红 向 华
(华中科技大学机械科学与工程学院国家数控系统工程技术研究中心,湖北 武汉 430074)
随着制造业的快速发展,各个行业对数控机床加工精度提出了更高的要求。导致机床精度下降的原因有很多,由于热变形产生的误差在机床总误差中占60%左右[1]。机床在内外热源的作用下开始膨胀,使得机床在加工过程中刀具和工件产生相对位移,进而导致加工精度下降[2]。
机床温升变形是指机床运动部件的摩擦发热引起的局部结构变形,而这种变形又导致温度急剧升高, 这两个方面是相互作用的。丝杠作为细长杆由温升变形所产生的热误差占有很大的比重。为了减小误差,提高机床的加工精度通常的解决办法是降温和补偿两种方法。降温的方法是将机床放置在恒温车间保持环境温度恒定,另外一种办法是给发热部件加装冷却系统,但这两种办法的成本都相当高,对丝杠的误差控制不明显,特别是丝杠在开机预热时变形量较大,即使在恒温车间内对于南方北方不同的地域、冬天夏天不同的季节所产生的变形量也不一样。所以,对热误差进行补偿是提高工件加工精度较为有效的方法[3]。
本文对工作台下的丝杠进行误差的测量分析,采用线性拟合的方法建立机床热误差的数学模型,将该模型集成在华中数控HNC-848的数控系统中对丝杠温度和误差数据进行采集和分析,实现机床的热误差补偿。
1 丝杠热误差的数据采集
依据三轴机床的X轴为例作为研究对象,与之相匹配的丝杠长度为500 mm。将两个温度传感器分别布置在与伺服电动机相连接的丝杠轴承座上和离远端轴承座40 mm处的位置上。机床在初始运行时,电动机的转速为3 000 r/min,环境温度为19.7 ℃,经过30 min预热,这时检测到丝杠温度升高了5 ℃。为研究丝杠的热变形规律,应用了Ansys软件进行了相应的热变形分析,如图1所示。可以看出丝杠靠近伺服电动机的一侧发热量最大,丝杠螺母处的发热量次之,故在发热量最大的热源点埋一个温度传感器,为了能够准确地测量出丝杠在不同温度下的伸长量,在远离伺服电动机460 mm处的丝杠中埋进了另一个温度传感器,该点的温度在整个丝杠中发热量最小。为测量丝杠在不同温度下的伸长量,采用了API激光干涉仪进行了现场测试。当时的环境温度为19.7 ℃,每升高1 ℃记录下丝杠的膨胀量,并计算出相邻两点间的斜率值,如表1所示。X轴的行程范围是[0,500 mm],测量起点为数控机床的坐标零点,测量的终点为数控机床的X轴坐标点460 mm处。

表1 温升与斜率统计表
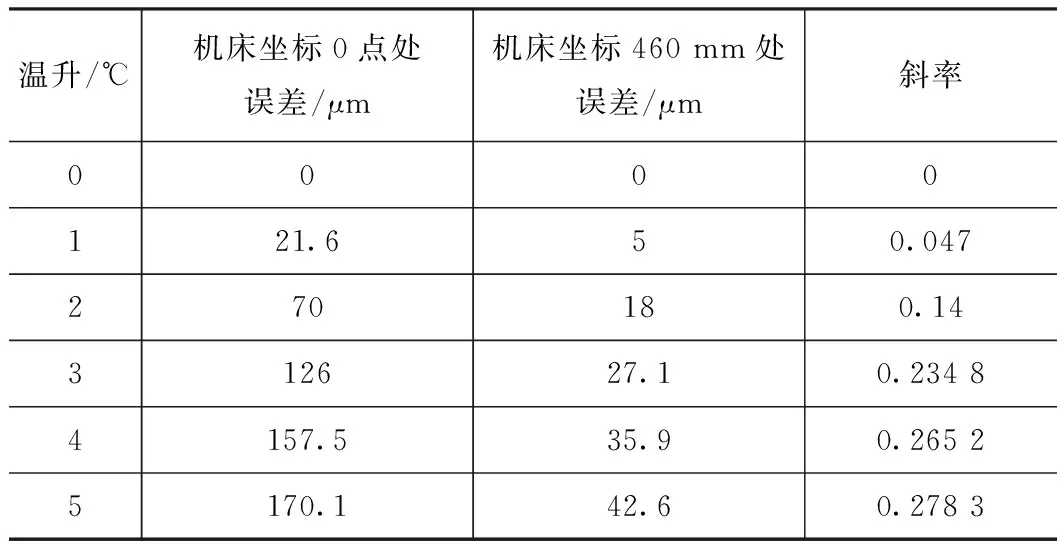
温升/℃机床坐标0点处误差/μm机床坐标460mm处误差/μm斜率0000121.650.047270180.14312627.10.23484157.535.90.26525170.142.60.2783
2 热误差建模
在约束条件下,丝杠的受热变形公式为
(1)
式中:L为丝杠的原始长度;ΔL为丝杠的热伸长;αT为线性膨胀系数;ΔT为温升;σ为热应力;E为弹性模量。ΔL/L用ε表示,由弹性力学可知ε=df(x)/dx,由此得出丝杠的一维变温热误差的微分方程为:
(2)
解式(2)得:
(3)
式中:T(x)为温度场函数,T=k1x+k2;C1=σ/E
根据边界条件可得式(2)的解。利用最小二乘法,对丝杠的温升和产生的热误差曲线进行拟合,拟合结果见图2。
根据以上的分析可得出以下表达式:
f(x)=0.1386x2+5.103x+2.779
式中:x为温升值,℃;f(x)为误差补偿值,μm。

3 热误差补偿分析

热误差补偿是指人为地创建一个新的误差来抵消当前成为问题的原始误差[4]。机床开始起动时会经历一个从冷态到热态的过程,此次机床的热变形最严重,丝杠的热伸长最快,以后逐渐减少并趋于稳定,停机后机床温度下降丝杠开始回缩,为了减小温度变化带来的加工误差,可采用预热机床减少停机来保持机床的热平衡[5]。
由于丝杠在环境温度高的情况下伸长量较大,可采取的措施是利用丝杠上所埋的两个温度传感器采集的温度差值作为热膨胀补偿的起点。机床开机运行60 s后开始实验,在华中数控HNC-848的数控系统中进行参数设定,如表2。
将计算得到的热误差值通过外部机床坐标系偏移(原点平移)叠加到位置控制信号中,从而实现热误差的实时补偿,其补偿原理见图3。在加工开始后,打开HNC-848系统的温度补偿模块,数控系统会每隔一分钟读取一次温度值,通过集成在内的补偿模型计算热误差的补偿值,再发出相应的控制指令以实现在线实时补偿。
表2 华中数控HNC-848系统参数设置表
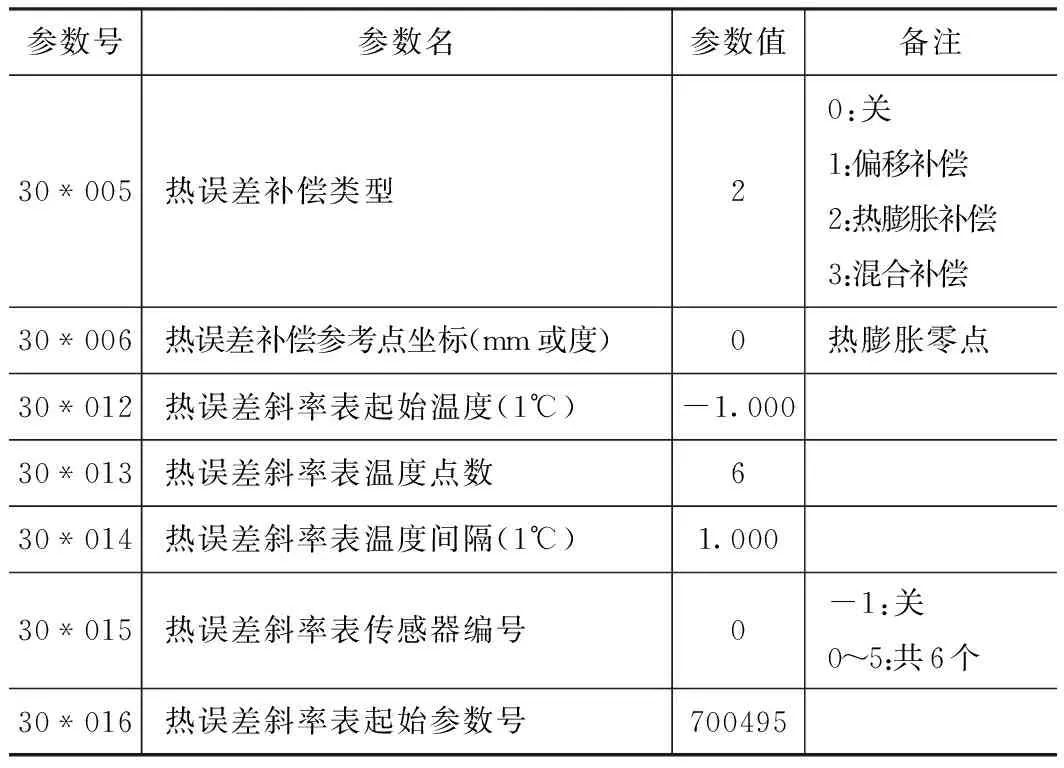
参数号参数名参数值备注30*005热误差补偿类型20:关1:偏移补偿2:热膨胀补偿3:混合补偿30*006热误差补偿参考点坐标(mm或度)0热膨胀零点30*012热误差斜率表起始温度(1℃)-1.00030*013热误差斜率表温度点数630*014热误差斜率表温度间隔(1℃)1.00030*015热误差斜率表传感器编号0-1:关0~5:共6个30*016热误差斜率表起始参数号700495

4 热误差补偿效果验证
在数控系统的热误差补偿关闭时,测试一组数据;然后打开热误差的补偿再测试一组数据。这两组数据为补偿前后的值,所使用的测量仪器为API激光干涉仪,测量环境为机床热机30 min后对三轴机床的X轴进行检测,补偿前后的效果如图4所示。图中虚线表
示正向和反向的平均值,由此可以得出补偿前机床的正反向误差范围是[-7 μm +6 μm],补偿后机床的正反向误差范围是[-1μm +9μm],公差范围由13 μm减小到10 μm,误差减小了23.1%,补偿效果较为显著,机床的精度有了较明显的提高。
5 结语
在华中数控HNC-848的数控系统中,这种补偿方法是依据所建立的数学模型和相应的处理软件集成在数控系统中实现的。通过此方法可在丝杠的不同温度状态下进行实时补偿从而达到提高数控机床精度的目的。
针对机床热误差补偿技术仍有以下两个方面有待进一步研究:
(1)当前的测量和建模是基于升温的基础上进行的,如果将机床的温度升到最高点,每下降1 ℃采集一次数据,这样建立的模型是否更优。
(2)温升范围扩大,所产生的拟合曲线是否更精确,补偿的效果是否会更好。
[1]Pekienik J, Jerele A. Some basic relationships for identification of the machining process[J]. CIRP Annals-Manufacturing Technology, 1992, 41(1):155-159.
[2]E Creighton, A Honegger, A Tulsian, et al. Analysis of thermal errors in a high-speed micro-milling spindle[J]. International Journal of Machine Tools & Manufacture, 2010(50): 386-393.
[3] Xu Z Z, Liu X J, Kim H K, et al. Thermal error forecast and performance evaluation for an air-cooling ball screw system[J]. International Journal of Machine Tools & Manufacture, 2011(51):605-611.
[4] 杨建国,任永强,朱卫斌,等. 数控机床热误差补偿模型在线修正方法研究[J]. 机械工程学报,2003,39(3):81-84.
[5]Josef Mayr,J Jedrzejewski,E Vhlmann, et al. Thermal issues in machine tools[J]. CIRP Annals-Manufacturing Technology, 2012(61):771-791.

