基于振动信号频域分析法的铣齿机故障诊断*
王志永 杜伟涛 王习文 陈 杨
(中南林业科技大学机电工程学院, 湖南 长沙 410000)
随着汽车工业、航空航天、工程机械等领域的快速发展,以及机械制造行业对产品质量标准的快速提升,市场对螺旋锥齿轮的需求越来越大,对其制造精度要求也越来越严苛。螺旋锥齿轮的制造精度、加工质量一直是业内所关注的焦点,而螺旋锥齿轮的制造水平取决于数控螺旋锥齿轮铣齿机的精度、稳定性及可靠性等技术指标[1]。目前,国产铣齿机在加工螺旋锥齿轮时存在明显的振动现象,所加工的齿轮齿面存在明显的振纹,切屑也呈现出异常的“屑花”状。这些故障的出现不但严重制约了齿轮精度的提升,而且极大地削弱了机床和刀具的使用寿命[2]。研究表明,异常振动是旋转机械产生故障的重要因素,机械振动信号的时域波形特征、数理统计数据、频谱特性能反映机械故障的类型和程度[3],通过对其振动信号的分析处理是进行机械故障诊断、衡量机械运行状态的重要手段[4-6]。
在基于振动信号的机械故障诊断技术中,常用的特征信号提取算法包括时域分析、频域分析和时频分析3种[7-8]。李舜铭等对振动信号处理方法进行了综述,阐明了频域分析法在机械故障诊断中的重要作用[9];王金福和李福才对时域分析、频域分析和时频分析的方法分别进行了理论阐释[7, 10];Vikas Sharma和Anand Parey利用频域均值法对齿轮箱的故障信号进行了处理,削弱了脉动速度对信号的影响,并提取了微弱的特征信号[11];Tristan Plante等利用振动信号的频域特征对旋转机械的运行状态异常与否进行了辨识[12];陈虹微对离心压缩机的振动信号利用频域分析法进行了处理,对转子不平衡的特征频率进行了提取,对转子不对中的波形特征进行了阐述,并利用故障诊断技术对离心压缩机的转子不平衡和不对中故障进行了诊断[13];时修丽等基于LMS Test lab对数控转台系统的工作状态进行了振动测试,并对测试信号进行了频域分析[14];朱培鑫对振动信号的频域分析法进行了描述,介绍了频域分析中的数理统计特征的算法,描述了振动信号统计数据与机械故障诊断的一般规律[15]。
频域分析法作为利用振动信号进行机械故障诊断的一种常用方法,目前主要是对机械故障进行定性诊断,鲜见利用频域分析法对机械振动信号的精确分析和故障识别。本文以H650C高速干切数控螺旋锥齿轮铣齿机为研究对象,通过振动信号的采集,并利用频域分析法对振动信号进行分析处理,将信号分析处理结果与关键部件的特征频率进行对比分析,从而实现对铣齿机刀具主轴系统的故障进行精确识别的目的。
1 铣齿机结构和受力分析
铣齿机作为螺旋锥齿轮的核心制造装备,其性能的优良直接影响着螺旋锥齿轮的制造水平,反映着一个国家的制造业水平。为了摆脱国外工业强国对螺旋锥齿轮的技术垄断,国内学者于上世纪七十年代对螺旋锥齿轮的制造原理展开了技术攻关,并在制造理论方面取得了重大突破。但是,由于齿轮制造装备技术积累有限,国产螺旋锥齿轮铣齿机在加工精度、可靠性、稳定性等方面与国外同类产品仍存在一定的差距。
1.1 铣齿机结构
H650C数控螺旋锥齿轮铣齿机是六轴五联动高档数控机床,能够实现Gleason齿制和Oerlikon齿制螺旋锥齿轮的高速干切工况加工。机床结构如图1所示,图中A轴是工件主轴,C轴是刀具主轴。

1.2 铣齿原理及受力分析
由螺旋锥齿轮的铣削方法可知,在螺旋锥齿轮的铣削加工中,刀具切削工件的过程是一个进给量不恒定的分层铣削过程,其切削原理如图2所示。



依据铣齿机铣削齿轮时的实际工况可得出:图3所示的刀具主轴和工件主轴的铣削位置关系,图中wA、wc分别代表工件主轴和刀具主轴的转向,β是工件主轴轴线与刀具主轴轴线的夹角。经过前期理论推导和实验测试结果表明,可将工件主轴上的铣削力矩关系等效到刀具主轴上,如图4所示。在图4中,Tc为刀具主轴上的铣削力矩,TA1和TA2分别为工件主轴上的切向铣削力矩与轴向铣削力矩。
1.3 刀具主轴系统的振动模型
在对机械设备进行振动分析时,需抽象出该机械设备的数学模型,尤其是对于精密机械设备,在构建其数学模型的过程中,更应将机械设备的细节和工况考虑详尽。一个振动系统的数学模型由机械设备的基本元件组成,振动系统中的元件一般分为刚性件、弹簧件和阻尼件三类[15]。
根据1.1和1.2节中铣齿机在工作过程中受力方式和铣齿机的机械结构进行综合分析,可知支撑主轴系统的轴承部分应重点考虑。其中轴承在运动过程中的内外圈间的相对运动关系,及运动过程中的阻尼特性,轴承外圈与轴承座之间的接触刚度,对主轴系统的振动特性具有一定的贡献。最后,依据振动模型的转换规则[16],可对刀具主轴系统的受力部件和运动部件进行等效处理,并构建如图5所示的H650C刀具主轴系统的振动模型。
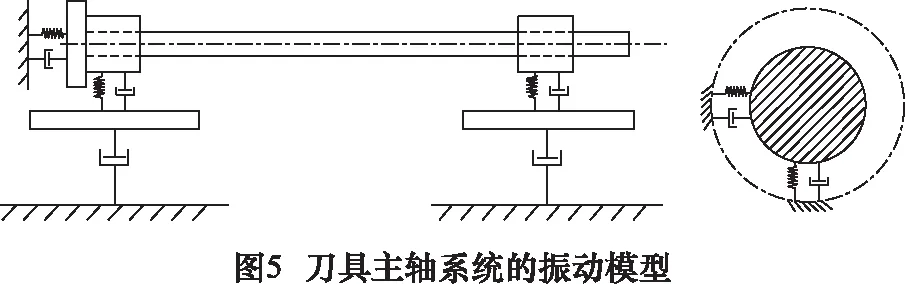
依照所建立的刀具主轴系统的振动模型的方法,同样可建立工件主轴系统的振动模型。从而可以设计基于铣齿机振动模型的振动测试实验,进而对铣齿机进行振动监测。
2 振动测试实验方案
根据刀具主轴系统的振动模型,可以通过实验方法对铣齿机进行振动性能的监测与分析,这属于典型的振动系统动力响应分析问题,即已知振动系统的激励和部分振动系统特性,分析验证振动系统的动力响应是否符合设计要求[15]。通过对系统进行振动实验是解决该问题的必要手段,因此,振动实验的设计直接决定了机械设备运行状态监测和故障诊断的结果是否可靠,是否准确。
2.1 仪器配置及选择
考虑到监测对象属于精密机械装备,因此在实验设备的选择上应力求实验数据的精确性和实验的可操作性。在传感器的选择上,选择综合性能较好的压电式加速度传感器,与速度传感器和位移传感器相比,其具有体积小,重量轻,频率响应范围宽,便于安放,成本低,适于测量高频、冲击信号,且耐温耐腐蚀性较好,不易损坏,可满足实验测试需求;信号采集装置利用具有多通道,高分辨率的Siemens公司的LMS Test lab数据采集前端主机,并采用低噪声级传感器专用连接电缆。
2.2 测点的优选
传感器布置位置的选择直接影响到振动测试信号的准确性,因此,传感器测点的选择应根据振动模型和测点位置的选取规则综合确定。一般传感器的测点位置选取应遵循如下的准则[17]:
(1)测点应选择在振动信号传递的通道上且路线最短捷的位置,尽量减少中间界面(近轴端)。
(2)选择能够反映机器工作状态,信号反应比较敏感部位做测点:轴承座、机座一般为典型测点。
(3)选定测点的同时,做好测点的定位标记,以保证测量信号的稳定性和可比性。因为即使在一个测点上,如位置稍有变化,其振动测量结果可能不相同。
(4)一般都要选定3个方向来评定振动,特别对低频振动,更要强调其方向性(高频振动无方向性)。
(5)对于大型机械设备,应作比较全面的规划,合理布置测点,精密诊断时还应考虑增加临时测点,多参数测振。
依据传感器布点规则和数控螺旋锥齿轮铣齿机的结构,建立如表1所示的传感器布置方案。
表1 传感器测点位置布置方案
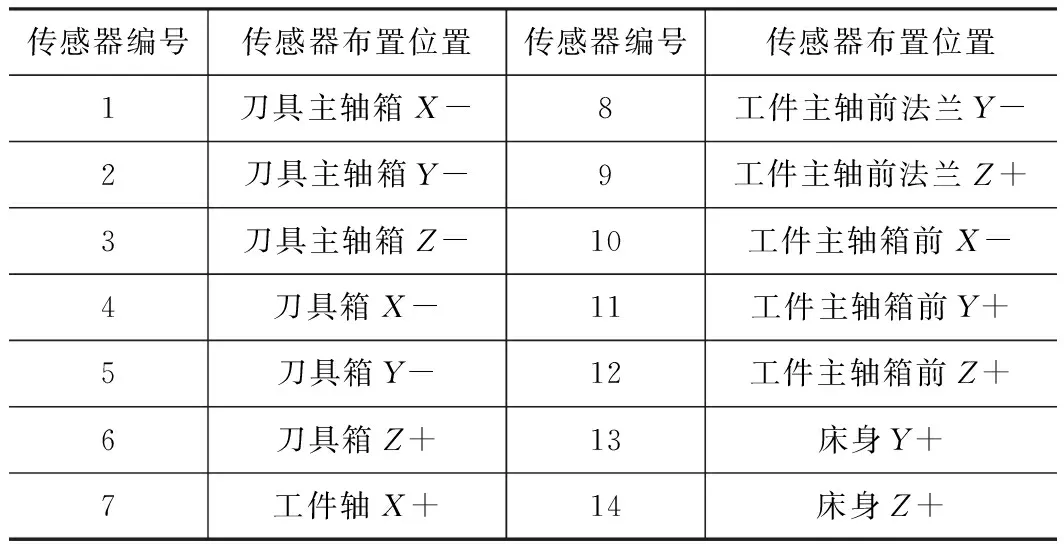
传感器编号传感器布置位置传感器编号传感器布置位置1刀具主轴箱X-8工件主轴前法兰Y-2刀具主轴箱Y-9工件主轴前法兰Z+3刀具主轴箱Z-10工件主轴箱前X-4刀具箱X-11工件主轴箱前Y+5刀具箱Y-12工件主轴箱前Z+6刀具箱Z+13床身Y+7工件轴X+14床身Z+
铣齿机三维模型和传感器布点方案配置如图6所示。
2.3 测试方案
根据铣齿机在工作过程中的实际故障情况和测点的选择,分为以下5种工况分别进行振动测试。
工况1:采集机床所在环境下的背景噪声。
工况2:刀具主轴空转,工件主轴不动,并实现转速分级。
工况3:工件主轴空转,刀具主轴不动,并实现转速分级。
工况4:工件主轴和刀具主轴联动,并实现铣削下的不同铣削速度。
工况5:刀具主轴和工件主轴联动,对工件进行正常工况下的铣削,实现不同齿制齿轮,不同规格齿轮的铣削。
按上述实验方案对铣齿机主轴系统进行振动实验,加速度传感器将振动信号采集后经数采前端保存到计算机中进行存储,从而得到被监测设备的振动信号。

3 振动信号的频域特征信息处理
机械设备故障的发生、发展通常会造成振动信号的频率发生变化,由机械故障(尤其是早期故障,轻微故障)所引起的振动,其特征信号很难从时域信号中提取出来,但振动故障在振动信号中会存在对应的频率成分[10]。在振动信号的处理过程中,将振动信号从时域转换至频域并做分析,在频域中以去粗取精的方式——使用不同方法对振动信号进行处理,从振动信号中提取出感兴趣的频率成分,对振动信号的特征进行识别,以实现机械故障诊断的目的。
3.1 时频转换方法
频域分析主要是建立在Fourier级数和Fourier变换基础上的振动信号分析方法,处理得到的结果是以频率为自变量的函数,称之为谱函数。由于实验采集到的信号为离散时域信号,离散时域信号的Fourier变换采用DFT方法。对于离散时域信号x[n](0≤n≤N)的Fourier变换X[k]如式(1)所示[18]。
(1)
利用DFT方法将振动信号从时域转换到频域后,即可得到振动频率和振动幅值大小关系的频谱图。通过对幅值谱的分析可以解决以下问题[10]:(1)得出频率分布的范围和振动频率成分。(2)得出各个振动频率成分和幅值之间的大小关系,据此可分析出对设备运行状态贡献较大的频率值及幅值大小。
在频谱分析中,截断和泄漏是在DFT变换中不可避免的。通常,使用窗函数对信号进行截断,截取有限的振动信号进行数据分析处理,这样便会产生能量的泄漏。为了减少能量的泄漏,通常依据表2中窗函数的修正系数K及其特点进行选取。
加窗处理时选用窗函数一般要求:主瓣宽度尽可能窄,且旁瓣高与主瓣高之比尽可能小,旁瓣幅值衰减速度快。对于一个振动信号,如果不作任何加窗处理而直接进行频谱分析,则实际上就是加了Rectangular窗。所以,在处理机械振动信号时,窗函数的选用一般遵循如下规则:对随机和周期激振信号,多用Hanning窗;对瞬态激振、自由衰减的信号,多用Gauss窗[18]。
表2 常用窗函数的修正系数及特点
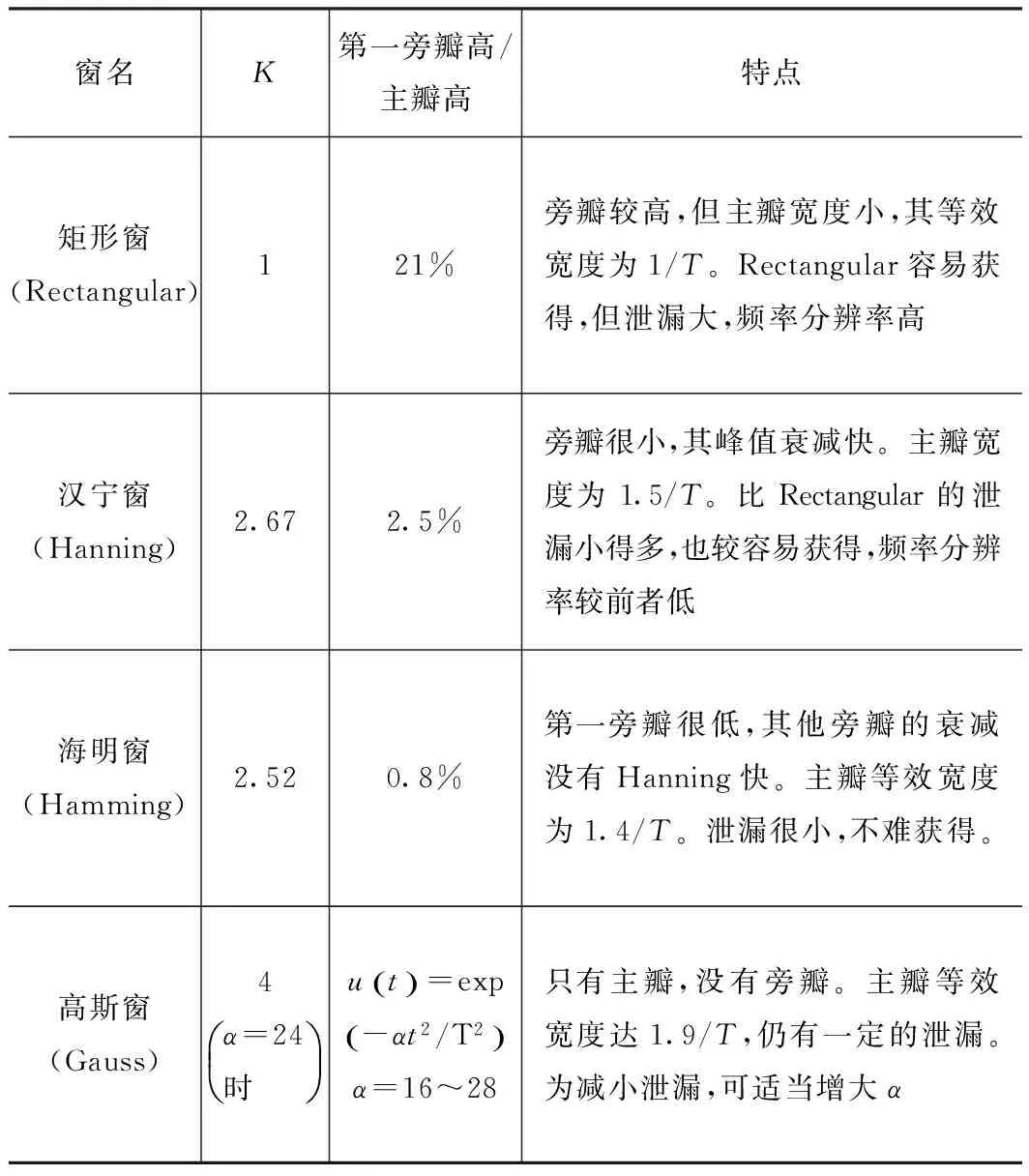
窗名K第一旁瓣高/主瓣高特点矩形窗(Rectangular)121%旁瓣较高,但主瓣宽度小,其等效宽度为1/T。Rectangular容易获得,但泄漏大,频率分辨率高汉宁窗(Hanning)2.672.5%旁瓣很小,其峰值衰减快。主瓣宽度为1.5/T。比Rectangular的泄漏小得多,也较容易获得,频率分辨率较前者低海明窗(Hamming)2.520.8%第一旁瓣很低,其他旁瓣的衰减没有Hanning快。主瓣等效宽度为1.4/T。泄漏很小,不难获得。高斯窗(Gauss)4α=24时æèçöø÷ut()=exp-αt2/T2()α=16~28只有主瓣,没有旁瓣。主瓣等效宽度达1.9/T,仍有一定的泄漏。为减小泄漏,可适当增大α
对采集到的H650C铣齿机的振动信号,利用FFT方法并加Hanning窗将信号从时域转换到频域上。据此可以得出各传感器采集到的振动信号的频谱图,如图7所示(1#传感器测得信号),从此频谱图中可以辨识出信号中较为明显的频率信息和幅值大小。

从图4所示的力矩关系图中可得出,刀具主轴径向和轴向承受的周期性铣削力方向、大小均不同。将监测到的两组振动信号(刀具主轴径向和轴向)转换至频域,得到图8所示的频谱图。从图8中可观察出主轴的径向和轴向各阶工频及其所受冲击的大小。图8中的频谱信息显示,主轴径向监测到的信号振幅较主轴轴向的大,故主轴径向的刚度劣于主轴轴向的刚度。

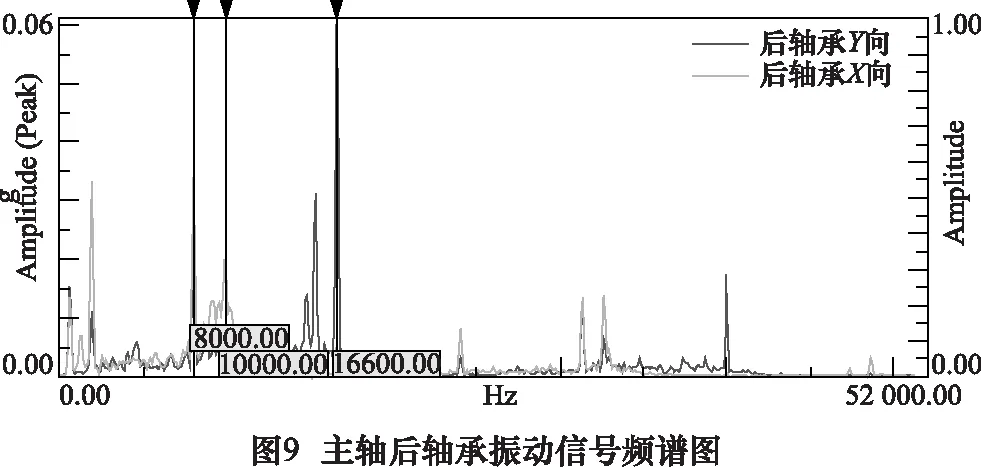
在刀具主轴系统中,刀具主轴由一对圆锥滚子轴承支撑,这对轴承性能优劣及装配是否合理直接影响着刀具主轴系统的刚度和阻尼特性,通过对振动信号分析可以看出轴承的运行状况。通过振动信号的频谱图可以对主轴前后轴承的运行状况进行分析,以解读出其频率信息。主轴前后轴承的频谱图如图9和图10所示。从图9和图10中可知主轴前后轴承的各阶工频和所受冲击的大小,对比观察两幅图可知,在低频范围内,主轴前轴承对振动信号更敏感,因此主轴前轴承的刚度较主轴后轴承略差,而且主轴后轴承X向和主轴前轴承Y向在8 kHz、10 kHz和16.6 kHz处存在明显的冲击信号。
将振动信号从时域转换到频域,可以从宏观角度分辨出,机械设备刚度薄弱环节,及主要的频率成分。
3.2 相关分析诊断
在振动信号的分析处理中,利用自相关函数与互相关函数对信号进行分析,可以对信号的某种内在联系进行诠释。对于一个随机振动信号,为了评价振动信号在不同时间的幅值变化相关程度,可以采用自相关函数;对于两个随机振动信号,可以定义相应的互相关函数用以表征其幅值之间的互相依赖关系。

在统计中,两个随机变量X、Y的相关函数定义如式(2)所示。
(2)
若X[n]是一个时域上的随机变量序列,将不同时间起始点的两个序列Xt1、Xt2看成两个随机变量,则相关函数表示为如式(3)形式。
(3)
如果X[n]是一个二阶稳态过程,即均值和方差不随时间而变化,此时相关函数只是时间差τ=t1-t2的一个函数,则式(3)可变为式(4)所示的自相关函数。
(4)
在信号处理中,随机信号x(t)可用式(5)所示的两时差函数的卷积来表示。
(5)
同理,对于两个振动信号x(t)和y(t),根据式(4)和式(5)可以得到其互相关函数Rxy(τ),如式(6)所示。
(6)
为了反映随机信号各频率成份功率能量的分布关系,揭示信号中隐含的周期性及靠得很近的谱峰等信息,通常采用具有统计特性的功率谱密度(PSD谱)对频域信号进行分析。根据式(6)和重积分性质,可推导出式(7)所示的自相关功率谱密度Rx(ω)。
(7)
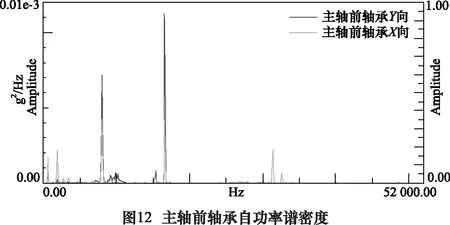
利用式(7)描述的自相关功率谱密度关系,对主轴前后轴承的振动信号求其自功率谱密度,可识别振动信号的频率成份及相应频率处的振动能量,结果如图11和图12所示。
根据图11和图12可得出,在低频处,主轴前后轴承X向的振动能量较大,在中高频处,主轴前后轴承Y向的振动能量较大。

3.3 对数谱分析
对数谱的实质是加权幅度谱,即对强信号采用小的加权,对弱信号采用大的加权[18]。幅值谱和功率谱都是所研究物理量的线性谱,由于许多微弱故障信号往往反映在振动信号的边带分量和谐波分量上,虽然其变化量级可以很大,但与其基波分量(往往是转频)相比,幅值仍然较小,甚至是相当微弱的。因此,在幅值谱或者功率谱上不容易观察到微弱信号的变化程度,这时常采用对数谱进行分析。通过对各频率分量的幅度取对数变为分贝(dB)量度单位的幅度谱,即为对数谱。转换关系如式(8)。
A(ω)(dB)=20lgA(ω)
(8)
根据图13所示的主轴径向和轴向振动信号的对数谱可明显看出,主轴径向振动信号波动幅度更大,表明主轴径向对冲击信号更为敏感,主轴轴向刚度优于主轴径向刚度;且主轴轴向信号的削弱速度较快,这也表明主轴轴向的阻尼较主轴径向的大。

3.4 特征信号的细化
通常对于随机振动信号,若要求某段频带有较高的频率分辨力时(如小阻尼、模态密集及耦合强的复杂系统),需通过增加数据的采样点数N,或增大采样步长Δt来提高Δf。在频域法分析中,常采用频谱细化技术提高信号处理的频率分辨力[19]。
频谱细化亦称为选带傅里叶分析。其基本原理是对需细化频段的信号进行移频、滤波、重采样处理[19],使该频段内的谱线变密。它是在采样点数N不变的条件下,在目的频段内提高Δf,使得选定频段的动态范围和分辨率都提高,便于识别振动信号细节处的频率特征。
基带Fourier分析是在0 ~fc频带内谱线均匀分布,所以,其频率分辨率为。
(9)
选带Fourier变换是为了提高分析谱线的分辨率,使分析的谱线在所选择的频带Δf内分布更清晰、特征更直观。此时的频率分辨力为。
(10)
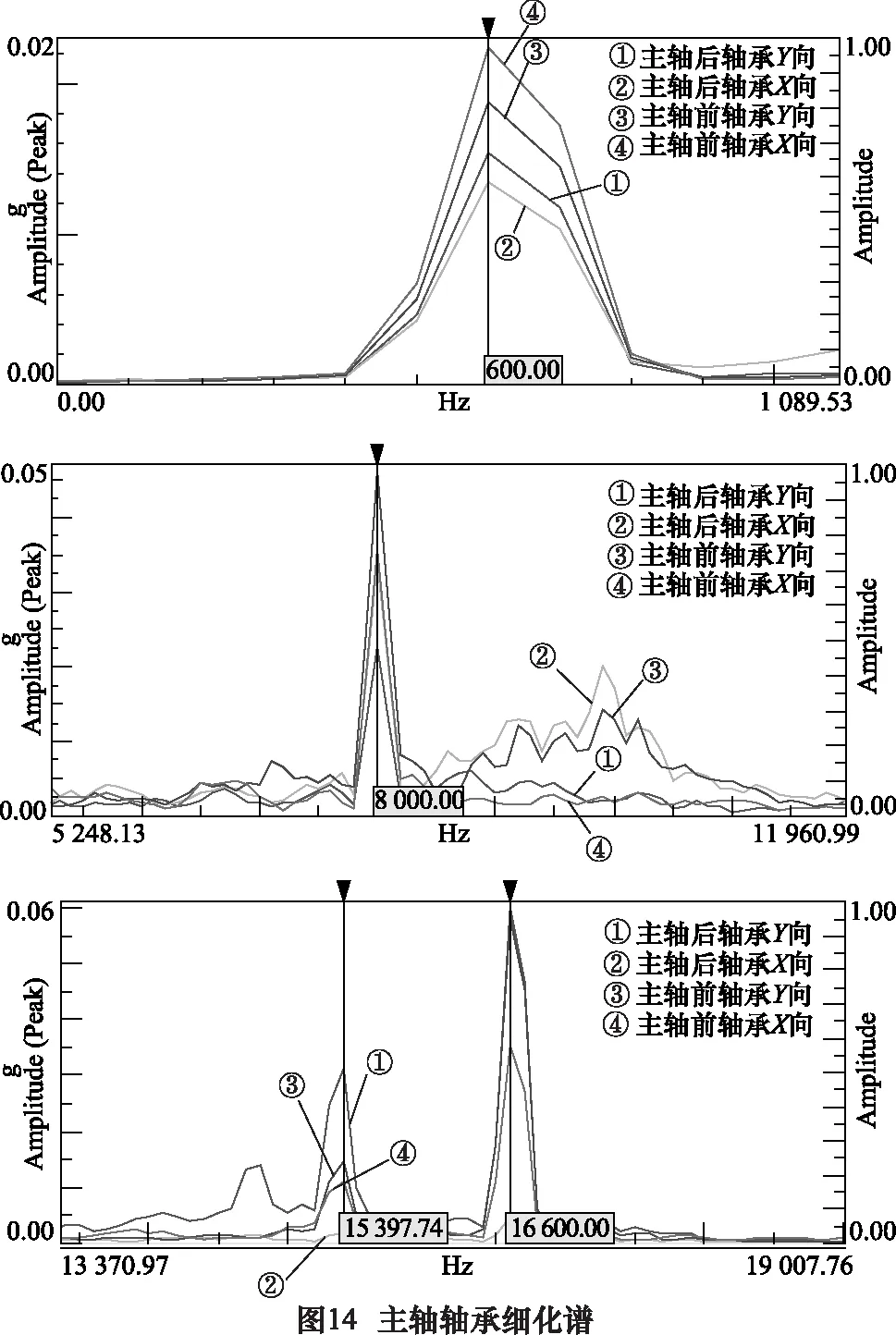
根据频谱细化方法,前述的分析结果,重点对主轴前后轴承X向和Y向振动信号进行频谱细化分析,得到图14所示的不同频率处的频谱特征细节。
根据图14所示的频谱细化图可以得出,主轴前后轴承在中低频处的振动频率及振幅大小关系。图14中所示,刀具主轴的前后轴承不同振动频率处的振幅却出现了明显的不同,且大小关系不一致,表明了刀具主轴存在动不平衡,刀具主轴的前后轴承装配刚度不一致引起刀具主轴工作过程中产生了复杂的偏心运动。
3.5 关键部件故障精确识别
对于机械设备而言,确定其固有特征频率是对设备进行精确故障诊断的基础。理想状态下机械振动信号的固有频率谱线是离散的,若机械设备的振动信号与其自身固有频率重叠,则会产生共振现象。由于共振现象的出现意味着在相应的固有频率处具有很大的能量,因此共振处峰值将会异常增大;对于大部分机械故障而言,并不会出现机械设备的共振现象,因此,若在设备固有频率谱线处的旁瓣较多,则意味着该固有频率处或该零部件处存在机械故障。
H650C铣齿机刀具主轴系统的回转零部件只有主轴和轴承。在正常工作过程中,刀盘铣削工件时的铣削力对刀具主轴造成冲击振动,本文铣削加工实验中所用的刀盘装有17组刀齿,在铣削过程中会产生铣削力冲击频率;轴承的结构也决定了其在工作过程中会产生振动冲击。
实验中刀具主轴系统采用的轴承为圆锥滚子轴承,精度P5级,滚子数量为35个,如图15所示。该轴承的关键技术参数如表3所示。
对于H650C铣齿机的刀具主轴系统,可根据表4计算得到主轴系统振动模型各零部件的固有特征频率[20]。
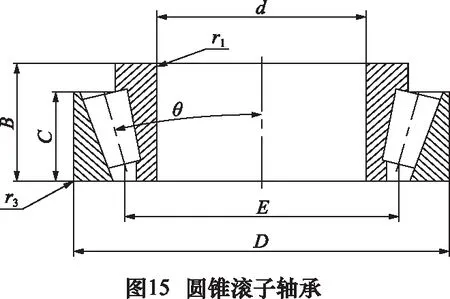
表3 轴承关键技术参数

D/mmd/mmB/mmC/mmE/mmθ/(°)230170393118829
表4 主轴系统固有特征频率

编号频率/Hz工况N1f=n/60轴的旋转频率N2f=n/120()1-d/D()cosθ[]外圈固定,保持架的旋转频率N3f=n/120()1+d/D()cosθ[]内圈固定,保持架的旋转频率N4f=n/120()Dd()1-d/D()2cos2θ[]外圈固定时滚动体的旋转频率N5f=z×n/120()1-d/D()cosθ[]外圈固定,外滚道上一固定点和滚动体之间的接触频率N6f=z×n/120()1+d/D()cosθ[]内圈固定,内滚道上一固定点和滚动体之间的接触频率N7f=n/60()Dd()1-d/D()2cos2θ[]滚动体上一个固定点和内外滚道的接触频率N8f=n/60()1-121-d/D()cosθ[]{}外圈固定,内滚道和保持架之间的相对旋转频率N9f=n/60()1-121+d/D()cosθ[]{}内圈固定,外滚道和保持架之间的相对旋转频率N10f=z×n/60()1-121-d/D()cosθ[]{}外圈固定,滚动体和内滚道上一固定点的接触频率N11f=z×n/60()1-121+d/D()cosθ[]{}内圈固定,滚动体和外滚道上一固定点的接触频率N12f=z×RPM轴承滚动体通过频率注:n—轴的转速,r/min;z—滚动体数目;d—滚动体的平均直径;D—滚动轴承的平均直径(滚动体中心处直径);θ等于节圆锥一半,对于向心球轴承或滚子轴承θ为零,对于向心推力轴承,θ是接触角。
根据表3和表4可以计算得出表5所示的主轴关键部件的固有频率。
表5 刀具主轴系统关键部件固有频率

项目铣削冲击频率N1N2N4N5N7N8N12频率/Hz150.174.4217.8619.77623.9939.544.189275
综合图14中的频率信息与表5中的计算结果分析可知,滚动体与轴承外圈某固定点的接触频率在低频处有体现,但是系统整体而言冲击作用不明显。轴承的滚动体通过频率在图14中无明显信息,但是在8 kHz和16 kHz处存在较强的冲击振动,对于本研究对象,主轴的不对中易引起这一情况。根据这两处的振幅情况可判断出,轴承和主轴均存在刚度不足的情况,因此冲击振动对系统作用效果明显,有较大的振幅;从波峰削弱趋势看,波峰衰减速度较快,表明系统的阻尼较大,有利于保持主轴系统的稳定运行。
机床制造企业根据上述分析结果,对刀具主轴做了动平衡校正,更换了轴承,对轴承的预紧力进行了重新设计,对影响主轴不平衡和轴承刚度的装配因素进行了严格控制。重新装配后的铣齿机,铣削加工齿轮时切屑不再成“屑花”状,所加工的齿轮表面质量有很大改善,机床的加工性能可满足工程实际的需求。
4 结语
本文以H650C高速干切数控螺旋锥齿轮铣齿机为研究对象,通过对铣齿机的力学分析,建立了铣齿机刀具主轴系统振动模型,依据振动系统模型对铣齿机进行了振动测试实验。
对采集到的振动信号进行了频域分析,在频域分析中利用多种信号分析方法实现了相关故障信号的特征识别。并将振动信号分析结果与刀具主轴系统关键零部件固有频率进行了对比分析。结果表明刀具主轴存在轻微不平衡,主轴前后轴承刚度不同,且主轴X向和Y向对振动信号的敏感程度也不一样,尤其主轴前轴承刚度欠佳。
本文所构建的机械设备振动模型、振动信号的监测和振动信号的处理方法,对于复杂机械结构进行基于振动信号分析的故障诊断具有借鉴价值。所引入的故障精确识别方法,可提高频域分析法在机械设备故障识别中的准确率。
[1]Wang Z. Correction of tooth flank errors of spiral bevel gear based on proportional change parameters[J]. Journal of Mechanical Engineering, 2010, 46(1): 43-47.
[2]Wang G. Basic research on machinery fault diagnosis—what is the prescription[J]. Journal of Mechanical Engineering, 2013, 49(1): 63-73.
[3]郝瑞卿. 基于振动信号分析的机械设备故障诊断研究[J]. 自动化与仪器仪表, 2016(5): 86-87.
[4]张君, 王金平, 朱波. 旋转机械振动信号处理中的滤波及特征提取技术[J]. 南京工程学院学报:自然科学版, 2009, 7(3): 14-21.
[5]Guo D, Peng Z K. Vibration analysis of a cracked rotor using Hilbert-Huang transform[J]. Mechanical Systems and Signal Processing, 2007, 21(8): 3030-3041.
[6]Plante T, Stanley L, Nejadpak A, et al. Rotating machine fault detection using principal component analysis of vibration signal [M]. IEEE Autotestcon. IEEE. 2016: 1-7.
[7]王金福, 李富才. 机械故障诊断技术中的信号处理方法:时域分析[J]. 噪声与振动控制, 2013( 2): 128-132.
[8]LEI Y. 2 - Signal processing and feature extraction [M]. Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery. Butterworth-Heinemann. 2017: 17-66.
[9]李舜酩, 郭海东, 李殿荣. 振动信号处理方法综述[J]. 仪器仪表学报, 2013, 34(8): 1907-1915.
[10]王金福, 李富才. 机械故障诊断的信号处理方法:频域分析[J]. 噪声与振动控制, 2013( 1): 173-180.
[11]Sharma V, Parey A. Frequency domain averaging based experimental evaluation of gear fault without tachometer for fluctuating speed conditions[J]. Mechanical Systems and Signal Processing, 2017, 85:278-295.
[12]Plante T, Stanley L, Nejadpak A, et al. Rotating machine fault detection using principal component analysis of vibration signal [M]. IEEE Autotestcon. IEEE. 2016: 1-7.
[13]陈虹微. 旋转机械振动特征及诊断方法[J]. 噪声与振动控制, 2009(1):134-137.
[14]时修丽, 黄筱调, 袁鸿, 等. 基于LMSTest_lab的数控转台振动测试研究[J]. 现代制造工程, 2012(9): 9-12.
[15]朱培鑫. 基于振动信号的旋转机械故障特征提取方法研究[D]; 哈尔滨:哈尔滨工程大学, 2014(3).
[16]张力, 刘斌. 机械振动实验与分析[M]. 北京:清华大学出版社, 2013.
[17]Singiresu S. Rao.机械振动[M].李欣业, 张明路,编译.北京:清华大学出版社, 2009(8).
[18]杨琴, 周亚丽, 张奇志. 在线参数辨识的脉冲噪声有源控制[J]. 噪声与振动控制, 2013(2): 138-143.
[19]徐平, 郝旺身. 振动信号处理与数据分析[M]. 北京:科学出版社, 2016(8).
[20]高大诚. 基于支持向量机的齿轮箱故障诊断系统开发[D]. 沈阳:东北大学, 2010.
[21]林选. 基于小波包和EMD相结合的电机轴承故障诊断[D]. 太原:太原理工大学, 2010.

