考虑非达西渗流的复合页岩气藏试井模型

王海涛, 彭 倩, 张烈辉, 郭晶晶, 聂 权

( 1. 西南石油大学 油气藏地质及开发工程国家重点实验室,四川 成都 610500； 2. 西南油气田公司 蜀南气矿,四川 泸州 646000 )

0 引言

随常规油气资源开采趋紧,包括页岩气在内的非常规资源的开发逐渐成为研究的热点[1-6]。页岩气藏作为自生自储式气藏[7],无论是在成藏机理、赋存方式方面,还是在渗流机理、渗流特征方面,都与常规气藏差异较大。页岩基质孔隙的大小从纳米到微米,页岩气赋存状态包括游离态、吸附态和溶解态,在页岩中具有多重运移机制：吸附—解吸、扩散、渗流等[8-9]。人们研究页岩气藏不稳定试井问题,建立多种动态模型[10-16],促进页岩气渗流理论的发展。其中压力和产量动态模型几乎没有考虑气体在近井地带渗流规律的变化,因此很难准确地描述气体的渗流特征。页岩储层压裂实践表明,受剪切和滑移效应影响,页岩储层压裂时形成的不再是有限的数条压裂缝,而是纵横交错的裂缝网络。在近井地带缝网改造区,受裂缝网络的高导流能力及过流断面面积剧减的双重作用影响,可能出现非达西效应。在综合考虑吸附—解吸、扩散、非达西渗流(内区)和达西渗流(外区)等运移机制的基础上,笔者建立更接近实际生产的页岩气藏试井解释模型,并采用半解析法对模型进行求解。

1 非达西渗流

在对页岩储层压裂时,受剪切滑移作用影响,在压裂改造区形成的不再是有限条人工裂缝,而是纵横交错的裂缝网络。在近井地带缝网改造区,裂缝网络导流能力极高,加之近井区过流断面面积急剧减小,导致流体流动时流速过高,偏离达西渗流规律。

有关非达西渗流研究多基于两种方程。Forchheimer P[17]提出包含速度一次方和平方项的Forchheimer方程(二项式非达西运动方程),描述非达西流动现象：

(1)

式中：p为孔隙压力；L为多孔介质长度；μ为流体黏度；k为储层渗透率；v为流速；α为非达西渗流系数；ρ为流体密度。

Izbash S提出指数式方程,描述速度与压力梯度之间的非线性关系[18]：

(2)

式中：c为渗流系数,与流体及多孔介质的性质有关；n为渗流指数,0.5≤n≤1。

指数式方程是通过实验和工程实践总结出来,虽然不像二项式非达西运动方程那样有明确的力学意义,但是从数值特征上描述流体速度变化的全过程,且形式简单,便于推导应用,因此文中采用指数式方程表达非达西渗流现象。

2 物理模型

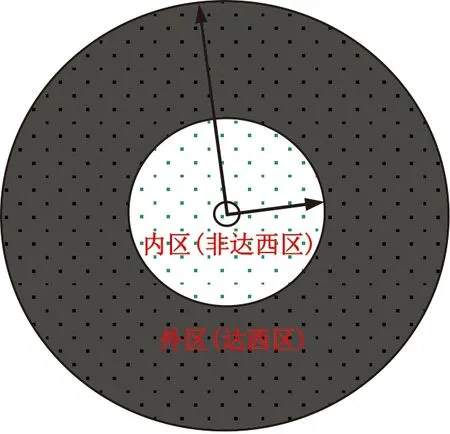
图1 考虑多重机制的双区复合页岩气藏模型

Fig.1 Schematic of a composite model in shale gas reservoirs with consideration of multiple migration mechanisms

考虑的页岩气藏渗流物理模型见图1。根据由缝网压裂等导致的孔渗物性差异,将页岩气藏的流动区域分为内区(1区)和外区(2区)。

基本假设：

(1)内区半径为R,外区考虑无限大外边界；

(2)气层厚度为h,气藏中各处原始地层压力为pi；

(3)内区服从非达西渗流,外区服从达西渗流,且存在吸附—解吸和扩散效应；

(4)页岩气吸附—解吸满足Langmuir吸附方程,扩散满足Fick第一扩散定律；

(5)气井以定产量qsc生产,忽略重力和毛细管力。

3 数学模型

借鉴Ikoku-Ramey对非牛顿流体渗流时的处理方法[19],扩展至高速非达西渗流：

(3)

(4)

式中：rw为井眼半径；psc为地面标况压力；T为气藏温度；Zi为原始条件下的天然气偏差因数；Tsc为地面标况温度。

式(3)实际上是将非达西渗流时惯性阻力的影响等效为表观渗透率k1a的变化：地层近井地带流速大,惯性阻力大,表观渗透率与地层本身渗透率(达西渗透率)相比下降幅度也大,因此表观渗透率小；反之,逐渐远离井壁时,地层渗流速度变小,惯性阻力变小,表观渗透率与地层本身渗透率相比下降幅度变小。假设在非达西渗流区域的外边界(内、外区的衔接面),非达西效应非常微弱,表观渗透率非常接近于地层本身渗透率：

(5)

其他无因次变量定义为

无因次拟压力

无因次时间

流度比

储容比

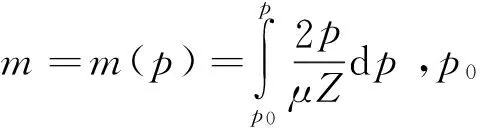
联立质量守恒方程、状态方程和指数式方程,经过拟压力化及无因次化,得到无因次复合页岩气藏内区渗流微分方程：

(6)

联立质量守恒方程、状态方程、运动方程、Langmuir等温吸附方程,经过拟压力化及无因次化,得到无因次复合页岩气藏外区渗流微分方程[16,20]：

(7)

其他定解条件：

m1D|tD=0=0,

(8)

m2D|tD=0=0,

(9)

(10)

m2D(∞,tD)=0,

(11)

m1D|rD=RD=m2D|rD=RD,

(12)

(13)

式(6-13)构成完整的考虑高速非达西渗流、达西渗流、吸附—解吸、扩散等机制作用的复合页岩气藏试井数学模型。

式(6)经过Laplace变换后将变为υ阶虚宗量贝塞尔方程,在Laplace空间的通解[19]为

(14)

式(7)经过Laplace变换后将变为零阶虚宗量贝塞尔方程,在Laplace空间的通解为

(15)

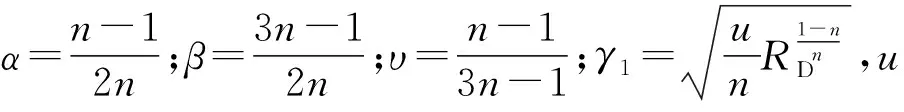
利用边界条件式(10-13),可以确定式(14-15)的4个未知数,计算井底压力需要确定系数A1和B1。为了简便起见,只给出井底压力解及必要的A1和B1的表达式：

(16)

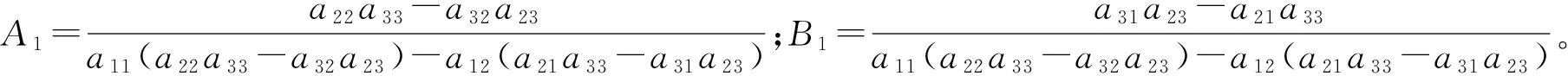
若考虑井筒储集效应和表皮效应,则关系式[21-22]为

(17)

式中：S为表皮因数；CD为井储因数。

4 模拟结果

4.1 典型曲线特征

考虑非达西效应等多重运移机制的复合页岩气藏试井典型曲线见图2,其中曲线参数CD=20,S=2.5,RD=300,M12=3,ω12=1.2,n=0.7。

根据曲线的形态,可划分流动阶段：(1)纯井筒储集影响阶段。该阶段双对数压力和压力导数曲线合二为一,呈斜率为1的直线,表明受续流段的影响。(2)过渡阶段。该阶段是从纯井筒储集效应向内区径向流阶段的过渡,导数曲线出现“驼峰”。(3)内区径向流阶段。该阶段压力导数曲线逐渐下降,原因是逐渐远离井筒时,惯性阻力逐渐减小,内区表观渗透率逐渐增大。(4)内区径向流向外区径向流的过渡阶段。由于内外区流度比M12>1,表明外区物性差,导数曲线上升。(5)外区径向流阶段。由于内外区流度比M12=3>1,表明外区物性差,压力导数曲线上升一个台阶后呈一条水平直线。

另外,为进行对比,假设渗流指数取为一个趋近于1的数,如n=0.999 9,流度比M12=1,储容比ω12=1,可以模拟内、外区为达西流的均质气藏的情形,并将它与传统的均质气藏模型进行对比(见图3)。由图3可以看出,两种模型计算的试井曲线基本重合,验证文中复合页岩气藏试井模型的正确性。

4.2 敏感性分析

4.2.1 渗流指数

不同渗流指数n时复合页岩气藏的压力和压力导数曲线见图4。由图4可看出,渗流指数对压力和压力导数曲线有较大的影响：n越大,越趋近于达西渗流,过渡段和内区径向流段的压力及压力导数曲线位置越低,表明达西渗流比非达西渗流消耗更少的能量。

4.2.2 内区半径

不同内区半径RD时复合页岩气藏的压力和压力导数曲线见图5。由图5可看出：RD越大,内区非达西渗流段持续时间越长,外区达西径向流段出现时间越晚。

4.2.3 内外区流度比

不同内外区流度比M12时复合页岩气藏的压力和压力导数曲线见图6。由图6可看出,导数曲线在“凹子”最深处向上抬升,然后逐渐变得平缓,形成另一条径向流水平线(外区径向流)。原因是压力波从内区传播到达外区后,外区的渗透性变差,从而导致压力损失加大。M12越大,压力导数曲线抬升幅度越大。

图2 复合页岩气藏的压力及压力导数曲线Fig.2 Pressure and pressure derivative responses of composite shale gas reservoirs

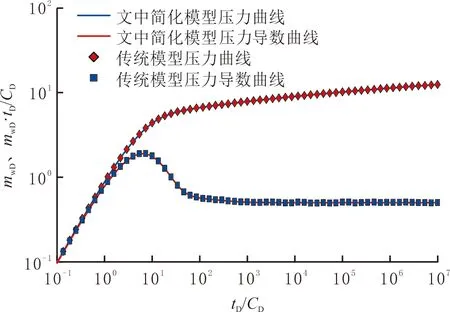
图3 文中简化模型与传统模型曲线

Fig.3 Comparison of transient pressure responses calculated by the reduced form of the proposed model in this paper and the typical model

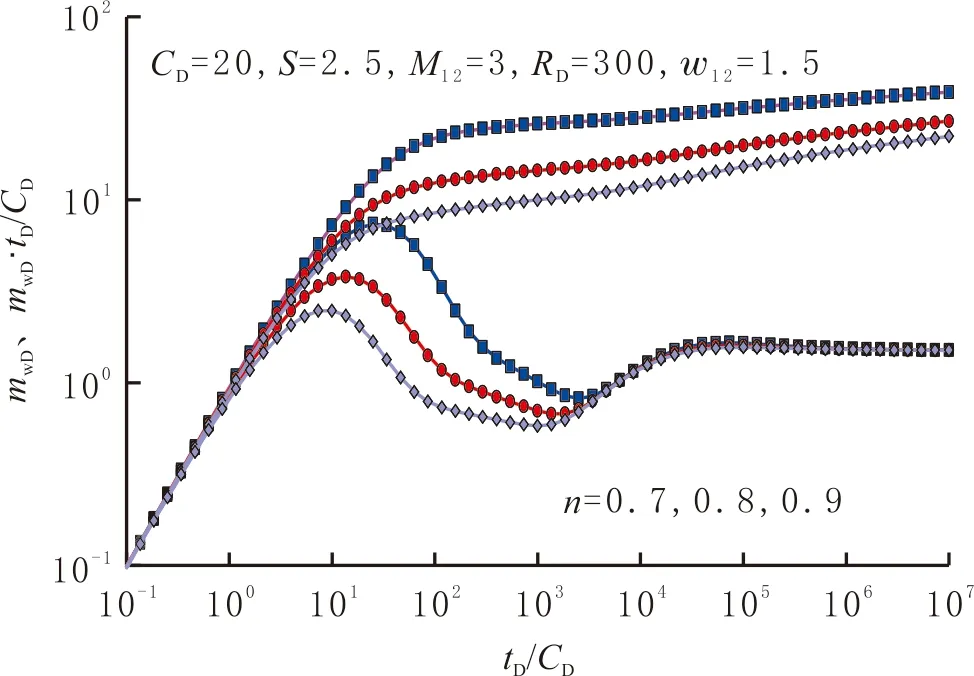
图4 渗流指数对复合页岩气藏压力响应特征曲线的影响Fig.4 Effect of seepage index on transient pressure behavior

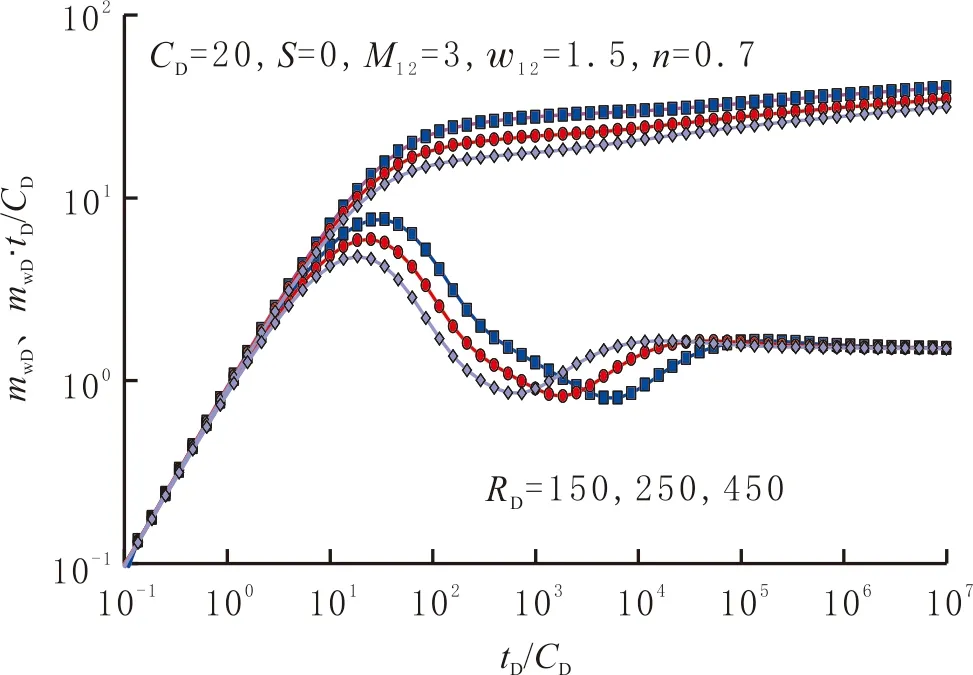
图5 内区半径对复合页岩气藏压力响应特征曲线的影响Fig.5 Effect of inner region radius on transient pressure behavior

4.2.4 储容比

不同储容比ω12时复合页岩气藏的的压力和压力导数曲线见图7。由图7可看出,改变储容比ω12,内外区过渡段后期出现峰值不同的小“驼峰”,ω12越大,“驼峰”的峰值越大。

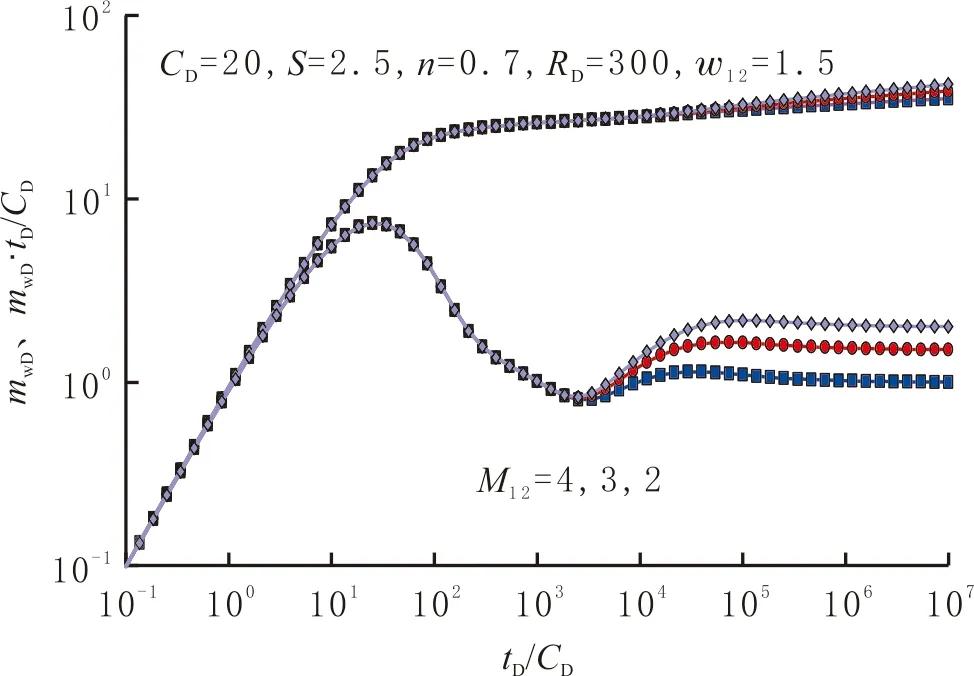
图6 流度比对复合页岩气藏压力响应特征曲线的影响

Fig.6 Effect of Mobility ratio between inner region and outer region on transient pressure behavior

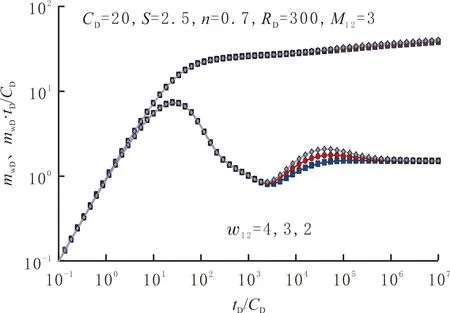
图7 储容比对复合页岩气藏压力响应特征曲线的影响Fig.7 Effect of storativity ratio on transient pressure behavior

4.2.5 扩散系数

不同扩散系数D时复合页岩气藏的压力和压力导数曲线见图8,其中k1=2×10-18m2,k2e=0.001×10-18m2,μ1=μ2=2×10-5Pa·s,φ1=0.04,φ2=0.02,ct1=ct2=3×10-8Pa-1,Ti=383K,Tsc=293 K,psc=105Pa,pL=2×107Pa,pi=3×107Pa,Zi=0.91。由图8可看出,D越大,外区径向流压力导数曲线位置越低。原因是随扩散系数的增大,外区等效渗透性变好,导致压力损失减小。

4.2.6 Langmuir吸附体积

在其他参数不变的情况下,不同Langmuir吸附体积VL时的压力和压力导数曲线见图9,其中k1=2×10-18m2,k2e=0.001×10-18m2,μ1=μ2=2×10-5Pa·s,φ1=0.04,φ2=0.02,ct1=ct2=3×10-8Pa-1,Ti=383 K,Tsc=293 K,psc=105Pa,pL=2×107Pa,pi=3×107Pa,Zi=0.91。由图9可以看出,改变VL,内外区过渡段后期出现峰值不同的小“驼峰”,VL越大,小“驼峰”位置越低,即与储容比ω12的影响结果相反。

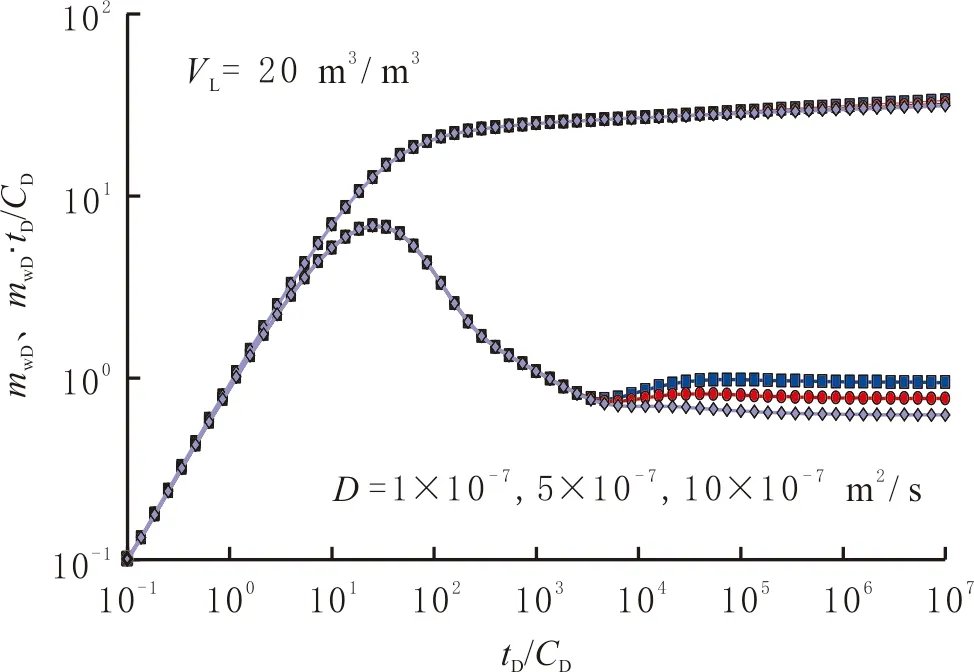
图8 扩散系数对复合页岩气藏压力响应特征曲线的影响Fig.8 Effect of diffusion coefficient on transient pressure behavior

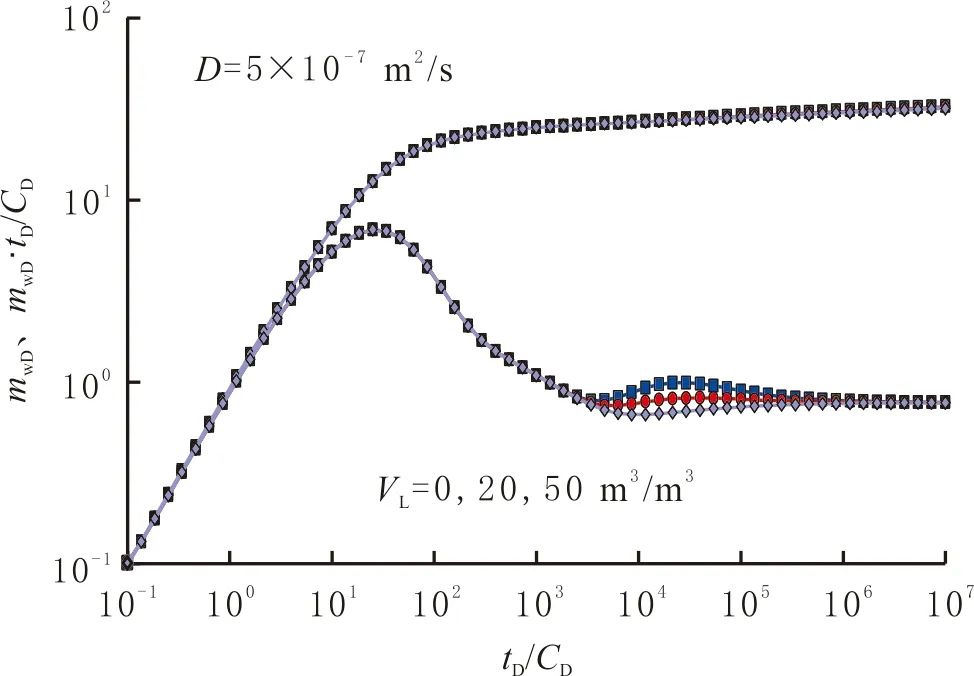
图9 Langmuir吸附体积对复合页岩气藏压力响应特征曲线的影响Fig.9 Effect of Langmuir volume on transient pressure behavior

井储因数CD与表皮因数S对典型曲线的影响与达西流的相同[23-25],不再赘述。

5 结论

(1)建立考虑非达西渗流的复合页岩气藏试井模型,在采用指数式方程描述近井地带非达西渗流现象同时,还考虑页岩气解吸、扩散和渗流运移机制。

(2)采用半解析法对模型进行求解,编程绘制试井典型曲线,并划分为纯井筒储集影响阶段、过渡阶段、内区径向流阶段、内区径向流向外区径向流的过渡阶段、外区径向流阶段5个典型的流动阶段。

(3)渗流指数越大,过渡段和内区径向流段的压力及压力导数曲线位置越低；内区半径越大,内区非达西渗流段持续时间越长；内外区流度比越大,外区径向流压力导数曲线抬升幅度越大；储容比越大,内外区过渡段后期出现的小“驼峰”的峰值越大；扩散系数越大,外区径向流压力导数曲线位置越低；Langmuir吸附体积越大,内外区过渡段后期出现的小“驼峰”位置越低。

[1] 邱振,邹才能,李建忠,等.非常规油气资源评价进展与未来展望[J].天然气地球科学,2013,24(2):238-246.

Qiu Zhen, Zou Caineng, Li Jianzhong, et al. Unconventional petroleum resources assessment: Progress and future prospects [J]. Natural Gas Geoscience, 2013,24(2):238-246.

[2] 闫存章,黄玉珍,葛春梅,等.页岩气是潜力巨大的非常规天然气资源[J].天然气工业,2009,29(5):1-6.

Yan Cunzhang, Huang Yuzhen, Ge Chunmei, et al. Shale gas: Enormous potential of unconventional natural gas resources [J]. Natural Gas Industry, 2009,29(5):1-6.

[3] 王公昌,姜瑞忠,徐建春.当前页岩气资源开发的瓶颈及建议[J].复杂油气藏,2012,5(2):10-14.

Wang Gongchang, Jiang Ruizhong, Xu Jianchun. Analysis and advice for shale gas development [J]. Complex Hydrocarbon Reservoirs, 2012,5(2):10-14.

[4] 江怀友, 鞠斌山, 李治平, 等.世界页岩气资源现状研究[J].中外能源,2014,19(3):14-22.

Jiang Huaiyou, Ju Binshan, Li Zhiping, et al. A study on the world's shale gas resources today [J]. Sino-Global Energy, 2014,19(3):14-22.

[5] 王世谦.页岩气资源开采现状、问题与前景[J].天然气工业,2017,37(6):115-130.

Wang Shiqian. Shale gas exploitation: Status, issues and prospects [J]. Natural Gas Industry, 2017,37(6):115-130.

[6] 曹园.页岩气资源开发的经济性评价[J].科技和产业,2017,17(4):73-75.

Cao Yuan. Economic analysis of shale gas development [J]. Science Technology and Industry, 2017,17(4):73-75.

[7] 王伟锋,刘鹏,陈晨,等.页岩气成藏理论及资源评价方法[J].天然气地球科学,2013,24(3):429-438.

Wang Weifeng, Liu Peng, Chen Chen, et al. The study of shale gas reservoir theory and resources evaluation [J]. Natural Gas Geoscience, 2013,24(3):429-438.

[8] 魏明强,段永刚,方全堂,等.页岩气藏孔渗结构特征和渗流机理研究现状[J].油气藏评价与开发,2011,1(4):73-77.

Wei Mingqiang, DuanYonggang, Fang Quantang, et al. Current research situation of porosity & permeability characteristics and seepage mechanism of shale gas reservoir [J]. Reservoir Evaluation and Development, 2011,1(4):73-77.

[9] 李智锋,李治平,苗丽丽,等.页岩气藏纳米孔隙气体渗流特征分析[J].天然气地球科学,2013,24(5):1042-1047.

Li Zhifeng, Li Zhiping, Miao Lili, et al. Gas flow characteristics in nano-scale pores of shale gas [J]. Natural Gas Geoscience, 2013,24(5):1042-1047.

[10] 段永刚,李建秋.页岩气无限导流压裂井压力动态分析[J].天然气工业,2010,30(3):26-29.

Duan Yonggang, Li Jianqiu. Transient pressure analysis of infinite conductivity fractured wells for shale gas [J]. Natural Gas Industry, 2010,30(3):26-29.

[11] Guo J J, Wang Haitao, Zhang Liehui. Transient pressure and production dynamics of multi-stage fractured horizontal wells in shale gas reservoirs with stimulated reservoir volume [J]. Journal of Natural Gas Science and Engineering, 2016,35,425-443.

[12] Wang H T. Performance of multiple fractured horizontal wells in shale gas reservoirs with consideration of multiple mechanisms [J]. Journal of Hydrology, 2014(510):299-312.

[13] Zhao Y L, Zhang L H, Luo J X. Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir [J]. Journal of Hydrology, 2014(512):447-456.

[14] Ozkan E, Brown M L, Raghavan R, et al. Comparison of fractured horizontal well performance in tight sand and shale reservoirs [J]. SPE Reservoir Evaluation & Engineering, 2011,14(2):248-259.

[15] Zeng Jie, Wang Xiangzeng, Guo Jianchun, et al. Composite linear flow model for multi-fractured horizontal wells in heterogeneous shale reservoir [J]. Journal of Natural Gas Science and Engineering, 2017,38:527-548.

[16] 姜瑞忠,滕文超,乔欣,等.复合页岩气藏压裂水平井压力动态分析[J].天然气地球科学,2015,26(12):2336-2342.

Jiang Ruizhong, Teng Wenchao, Qiao Xin, et al. Pressure transient analysis of fractured horizontal well in composite shale gas reservoir [J]. Natural Gas Geoscience, 2015,26(12):2336-2342.

[17] Forchheimer P. Wasserbewegung durch Boden [J]. Zeitschrift Verein Deutscher Ingenieure, 1901,45(5):1782-1788.

[18] Wen Z, Huang G H, Zhan H B. Non-Dareian flow toward a finite-diameter vertical well in a confined aquifer [J]. Pedosphere, 2008,18(3):288-303.

[19] Ikoku C U, Ramey H J Jr. Transient flow of non-Newtonian power-law fluids in porous media [J]. SPE Journal, 1979, 19(3):164-174.

[20] 廖新维,沈平平.现代试井分析[M].北京:石油工业出版社,2002:150-154.

Liao Xinwei, Shen Pingping. Modern well test analysis [M]. Beijing: Petroleum Industry Press, 2002:150-154.

[21] Van-Everdingen A F, Hust W. The skin effect and its influence on the productive capacity of a well [J]. Journal of Petroleum Technology, 1949,1(12):305-324.

[22] Kucuk F, Ayestaran L. Analysis of simultaneously measured pressure and sand face flow rate in transient well testing(includes associated papers 13937 and 14693) [J]. Journal of Petroleum Technology, 1985,37(2):323-334.

[23] 付春权,张波,姜英军,等.压力恢复试井理论曲线的特征[J].大庆石油学院学报,1998,22(4):30-33.

Fu Chunquan, Zhang Bo, Jiang Yingjun, et al. Characteristics build up curve in well testing theory [J]. Journal of Daqing Petroleum Institute, 1998,22(4):30-33.

[24] 吕秀凤,刘振宇,张瞳阳.数值试井分析的有限元法[J].大庆石油学院学报,2005,29(5):12-15.

Lyu Xiufeng, Liu Zhenyu, Zhang Tongyang. Finite element method of the numerical well test analysis [J]. Journal of Daqing Petroleum Institute, 2005,29(5):12-15.

[25] 方晓春,蒋鑫,刘启国,等.高含硫气藏两区复合地层试井解释方法研究[J].重庆科技学院学报:自然科学版,2013,15(5):36-39.Fang Xiaochun, Jiang Xin, Liu Qiguo, et al. Well test analysis method study of high sulfur two-block composite gas reservoir [J]. Journal of Chongqing University of Science and Technology: Natural Sciences Edition, 2013,15(5):36-39.