基于改进EF理论的梯级引水式电站生态环境影响定量评估

赵运吉

(岫岩满族自治县水利局，辽宁 鞍山 114300)

1 基本情况

农村引水式电站一般建在山丘型的河道上，也多呈现梯级分布的方式，引水电站的建设和运行方式也势必对区域生态环境产生一定的影响。当前，国内许多学者对梯级水利工程运行的生态环境影响定量评估进行了主要研究[1- 6]，这些研究采用的生态环境影响定量评估的主要方法为EF理论，通过EF理论来定量分析水利工程运行对区域生态环境的影响。但是传统EF理论未能考虑不同属性之间生态承载力的可比性，计算的生态EF值存在偏大的局限，为此有学者对传统EF理论进行改进，并在一些生态环境影响评估中得到具体应用[7- 9]，但是在农村引水式梯级电站的生态环境影响评估中还未进行相关应用，为此本文引入改进的EF理论，以辽宁东部某梯级引水电站为研究实例，对区域农村引水式梯级电站的生态环境进行定量评估。

在传统EF理论计算中，不同属性的生态EF值计算方程为：

A=∑Ci/Pi

(1)

式中，A—农村引水式电站各生态属性值；i—计算类型；Pi—第i类型的初级生产力；Ci—不同属性的环境影响程度。

改进的EF理论综合考虑生态承载可比性，对方程(1)进行了改进，改进方程为：

(2)

式中，Ag—改进的农村引水式电站各生态属性值；CM—区域生态承载力可比性调整系数。

其中改进的EF理论采用以下方程计算CM值，计算方程为：

(3)

式中，Ak—同期生态属性值；AM—不同时期生态属性值。

在农村引水式梯级电站生态属性确定的基础上，可计算各属性EF值，计算方程为：

EF=∑rjAg

(4)

式中，EF—改进EF理论计算的农村引水式电站EF值；rj—各生态属性的等价因子。在计算各分属性EF值后，可计算不同类型的生态EF值，计算方程为：

EFT=N×EF

(5)

式中，EFT—不同类型的生态EF总值；N—类型个数。在计算生态EF值的同时，改进的EF理论采用以下方程计算农村引水梯级电站的区域生态承载力，计算方程为：

EC=N(ajrjYj)

(6)

式中，EC—计算的区域总的生态承载力；Yj—不同类型的生态承载比；aj—不同类型所占的面积属性值。

2 基于改进EF理论的辽宁东部农村梯级引水式电站生态环境影响评估

2.1 研究区域梯级农村引水式电站概况

本文以辽宁东部某区域梯级农村引水式电子为研究实例，该区域内有5座农村引水式电站，各引水式电站的属性表见表1。结合区域各梯级引水式电站的属性表，结合不同算法对各农村引水式电站的生态EF值和生态承载比进行计算。

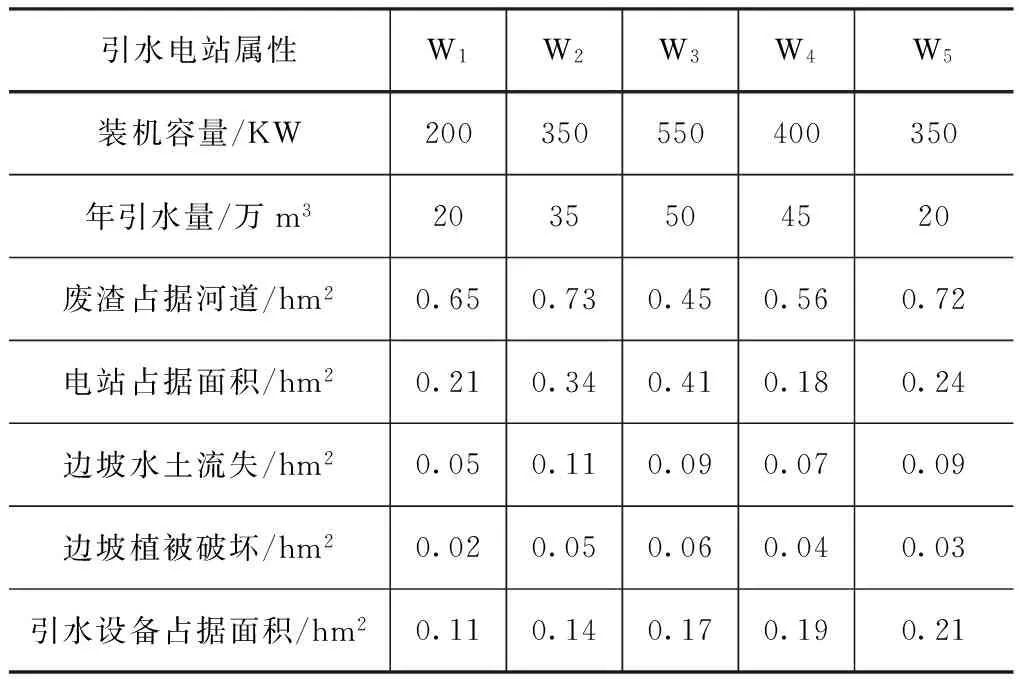
表1 辽宁东部各梯级引水式电站属性表

2.2 基于不同算法的区域梯级引水式电站生态影响定量评估

分别结合传统和改进EF理论对研究区域梯级引水式电站的生态EF值进行定量评估，分析结构见表2和表3。

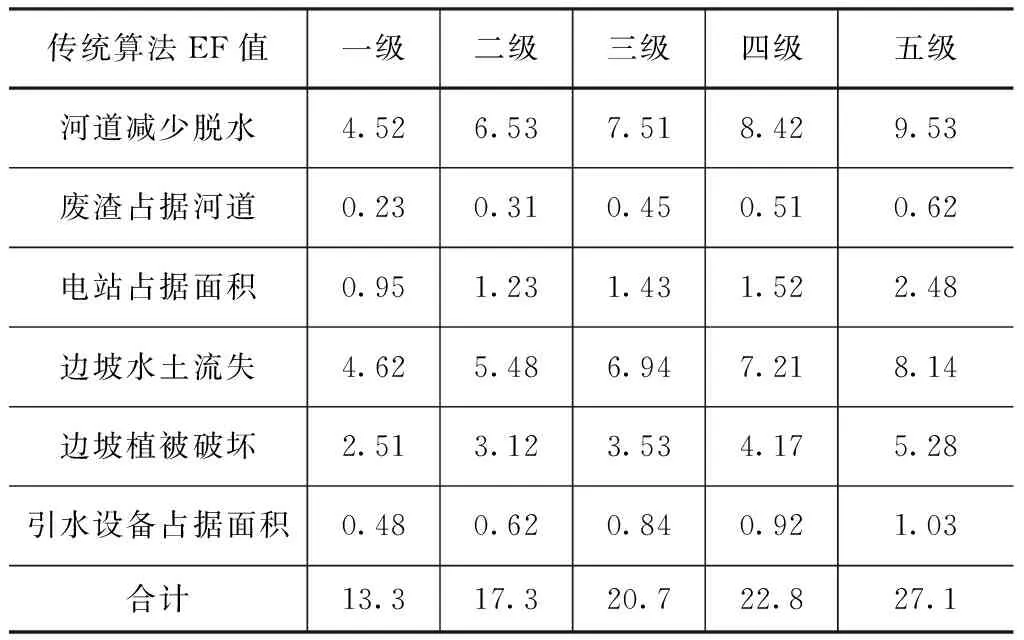
表2 传统算法下各梯级引水电站不同属性的EF计算值 单位：hm2

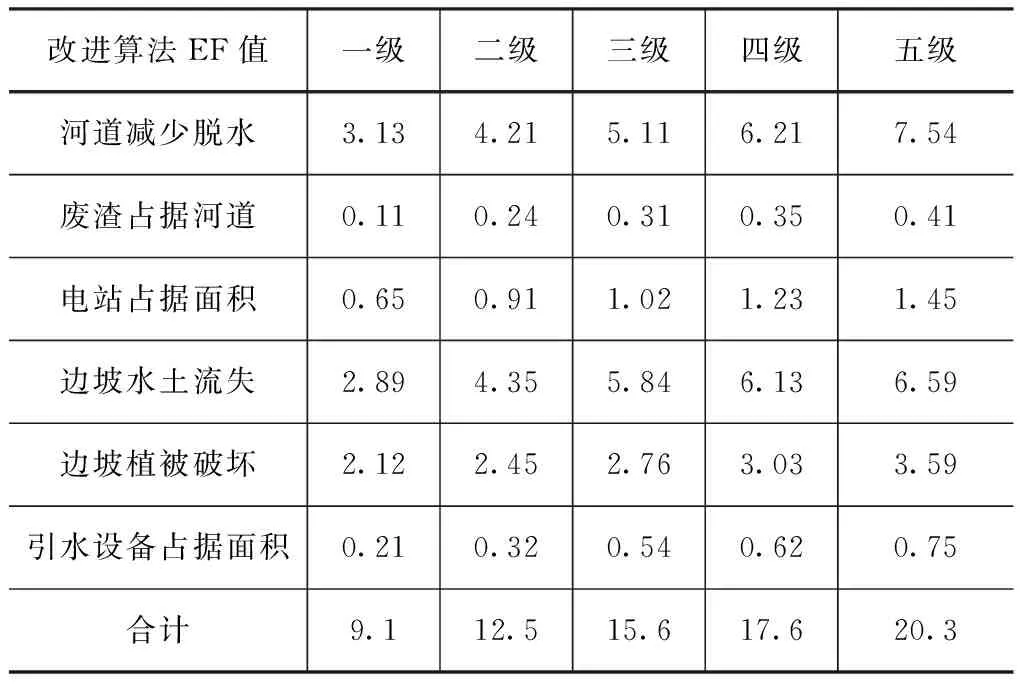
表3 改进算法下各梯级引水电站不同属性的EF计算值 单位：hm2

表2为传统算法下各梯级引水式电站不同级别的EF值，从表中可以看出，河道减水脱水和边坡水土流失的生态EF值在各类型属性中最高，各级引水式电站的生态EF值在4.52～9.53hm2之间，对生态影响高于其他类型。废渣占据河道的生态EF值最低，在0.23～0.62hm2之间，对区域生态环境影响低于其他类型。从表3中可以看出，各梯级电站不同类型的生态EF计算值均小于采用传统EF值，这主要是改进的EF理论综合考虑各类型承载允许比，使得计算EF值小于传统算法下的EF值。改进算法和传统算法下的各电站生态评估结果较为类似，但计算值小于传统算法。

2.3 基于不同算法的区域梯级引水式电站生态承载力定量评估

在生态EF值计算基础上，结合不同算法对区域梯级引水式电站的生态承载力进行评估，分析结果见表4和表5。

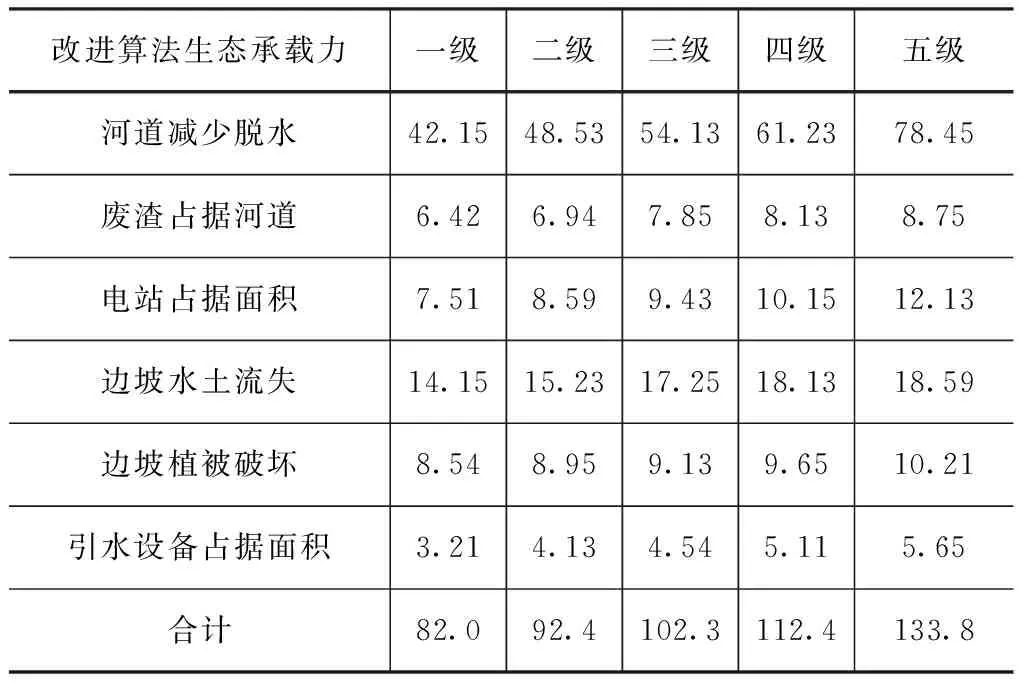
表4 传统算法下各梯级引水电站不同属性的生态承载力计算值 单位：hm2

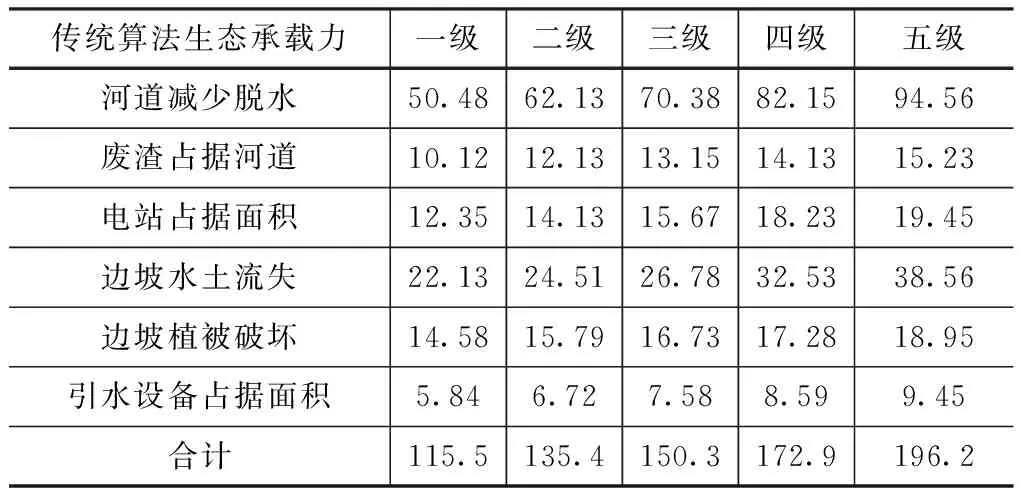
表5 改进算法下各梯级引水电站不同属性的生态承载力计算值 单位：hm2

从表4中可以看出，各级生态承载比呈现递增变化的特点，随着农村引水式梯级电站级数的增加，各类型生态承载力逐渐增加；引水式电站下河道减少脱水的生态承载力最高，区域各类型的生态承载力均指在82.0～133.8hm2。从表5中可以看出采用改进算法下各类型的生态承载力较传统算法都有所提高。

2.4 基于不同算法的区域梯级引水式电站生态环境变化百分比分析

结合不同算法下区域各梯级农村引水式电站的生态EF值和生态承载力计算值，对比分析不同算法下各区域梯级引水式电站的生态环境变化百分比，计算结果见表6和表7。

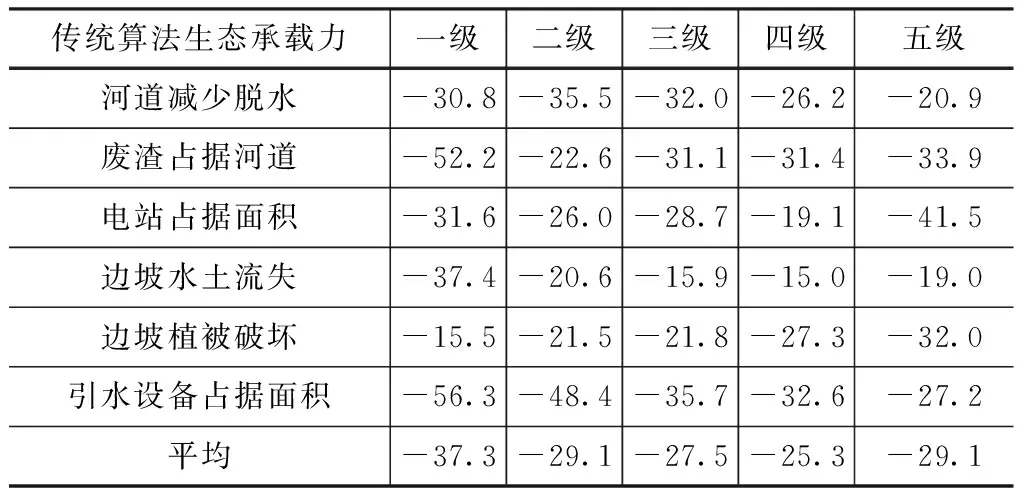
表6 不同算法下各梯级引水电站EF值变化百分比结果 单位：hm2

表7 不同算法下各梯级引水电站生态承载力变化百分比结果 单位：hm2

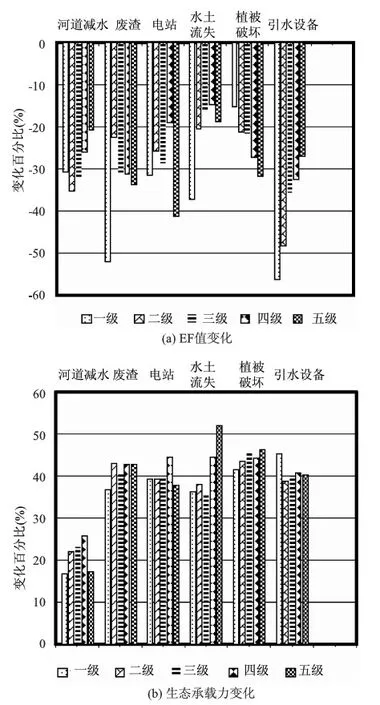
图1 不同算法下各级农村引水式电站生态环境变化百分比

从表6中可以看出，相比于传统EF理论，改进EF理论下的各梯级水电站的EF值都有所减少，各类型EF减少百分比均值在-29.1%～37.3%之间，生态EF值平均减少-29.7%，但生态EF值减少特点不明显。从表7中可以看出，改进EF理论下的各梯级农村引水式电站的生态承载力相比于传统EF理论均有所提高，这和区域的实际情况较为吻合，各类型区域生态承载力变化值在35.8%～40.2%之间，生态承载力相比于传统EF理论均值提高37.9%。从图1中可看出，引水电站边坡水土流失的生态EF和生态承载力变化最大，而河道减少脱水变化最小，可见引水电站边坡水土流失对该区域农村引水梯级电站的生态环境影响较大。

3 结语

本文结合改进前后的EF理论对辽宁东北某区域农村引水梯级电站的生态环境影响进行定量评估，评估结论为：

(1)改进后EF理论对降低了不同类型的生态EF值，对区域生态承载力计算值有所提高，适用性好于传统EF理论。

(2)辽宁东部研究取农村引水式梯级电站下的边坡水土流失和河道减少脱水对生态影响高于其他类型；废渣占据河道的生态EF值最低，在0.23～0.62hm2之间，对区域生态环境影响低于其他类型。

[1] 王智阳. 水利工程的生态环境影响及调控措施[J]. 黄河水利职业技术学院学报, 2011(04): 7- 9.

[2] 邹淑珍. 赣江中游大型水利工程对鱼类及其生态环境的影响研究[D]. 南昌大学, 2011.

[3] 庄益朋. 宫山咀水库环境安全保护对策探析[J]. 水利技术监督, 2017(01): 55- 56+141.

[4] 王慧斌. 水库生态调度的内涵与模型探析[J]. 水利规划与设计, 2016(03): 34- 35+107.

[5] 贾硕. 水利水电工程生态环境影响评价指标体系与评价方法的研究[D]. 河北农业大学, 2011.

[6] 赵鑫. 石佛寺水库生态修复若干问题及对策[J]. 水利规划与设计, 2015(11): 22- 23+37.

[7] 王国刚, 杨德刚, 张新焕, 等. 基于能值理论的生态足迹改进模型及其应用[J]. 中国科学院研究生院学报, 2012(03): 352- 358.

[8] 赵运林, 傅晓华. 生态足迹理论在长株潭城市生态安全研究中的应用与改进[J]. 城市发展研究, 2008(04): 127- 130+134.

[9] 王书玉, 卞新民. 生态足迹理论方法的改进及应用[J]. 应用生态学报, 2007(09): 1977- 1981.