高速铁路牵引供电系统负荷过程仿真技术的研究

张彦伟，郎 兵，李 应，刘 苹，施东和，赵 隽

（1.北京交通大学 电气工程学院，北京 100044；2.中国铁路昆明局集团有限公司 昆明供电段，昆明 650100）

我国高速铁路发展迅速，与普速铁路有很大不同的地方，如主要采用AT供电方式，牵引变压器采用V/X接线形式等，为了更好掌握高速铁路其特有的供电规律及特性，开展对高速铁路牵引供电系统负荷过程仿真研究很有必要。国内外对此也做了很多研究[1-5]。但由于传统的电气化铁道牵引供电系统仿真一般采取单一的供电系统仿真计算方法，忽略了供电系统和列车牵引运行的内在联系，从而影响了仿真结果的精度[6]。所以，本文先根据动车组的运行条件进行牵引计算，得到动车组运行到某一位置时所对应的速度以及取电功率，为后续牵引供电系统的潮流计算提供负荷数据。在牵引网负荷过程仿真计算中，建立了一次供电网络模型，推导了牵引变电所V/X接线牵引变压器模型，建立了牵引变电所两侧牵引网的数学模型，将一次供电网络、牵引变电所、牵引网、动车组负荷统一起来进行潮流计算，使牵引供电负荷过程仿真计算更加贴近实际情况。并且在潮流计算基础上模拟了动车行驶过程，可以动态的观察动车前进过程中牵引网电压电流的变化，而不是局限于动车处于某固定位置不变，这样能更加简单明了的观察在动车行进过程中，电压电流的变化规律。

1　列车牵引计算

高速动车组主要采用动力分散形式，对其进行牵引计算首先要对列车进行受力分析，计算其单位合力c。

式中，f为列车单位牵引力（由牵引特性曲线获得），单位：N/kN；w为列车单位全阻力（包括基本阻力和附加阻力），单位：N/kN；b为列车单位制动力（主要为再生制动），单位：N/kN。

根据列车所受合力推导列车运行加速度，并根据仿真步长计算下一时刻的速度：

式中，Δt为仿真中设置的时间步长，单位：s；cp为每个速度间隔内平均速度对应的单位合力，单位：N/kN；v1，v2为每个速度间隔对应的初速度和末速度，单位：km/h。

那么，每个时间间隔内列车运行的距离为：

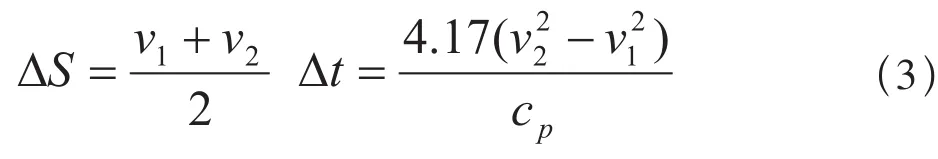
在列车牵引计算过程中，依据列车运行工况由当前运行速度通过查取牵引特性曲线确定轮轴牵引力F轴（单位：kN），轮轴牵引力与列车运行速度v（单位：km/h）的乘积即为当前列车的轮轴输出功率P（单位：kW）。

列车在受电弓处取电功率可以表示为：

式中，η为列车综合效率，一般取0.85；P辅助为列车控制设备和空调照明等辅助设备所需功率。

列车采用恒功率模型，功率值即为由牵引计算得到的取电功率 P取电。

列车在运行阶段，列车采用根据贴近限速及围绕目标速度的运行方式。当列车的运行速度比目标速度小时，列车按照牵引工况加速到目标速度运行，牵引力大于运行阻力；当列车速度接近当前路段目标速度时，列车围绕目标速度匀速运行，尽量保证牵引力等于运行阻力；如果列车速度不断增大到达限速时，列车将采用制动工况防止超速。

以下针对长昆客运专线邓家山变电所及其供电臂构成的牵引供电系统进行仿真计算，供电系统全长50.993 km，邓家山至白水分区所为α臂，全长20 km，在中间10 km处为高寨AT所，邓家山至廖家田分区所为β臂，全长30.993 km，在距邓家山变电所16.7 km处为窄沟沿AT所。CRH380A列车以300 km/h的初速度从白水分区所运行至廖家田分区所，其中线路最大坡度为24‰，最小曲线半径为7 005 m，仿真计算结果如图1所示。列车在整个行驶区间的速度围绕300 km/h匀速行驶，列车取电功率主要受坡度以及曲线半径的影响而波动，将此结果保存起来，作为牵引网潮流计算的负荷数据。

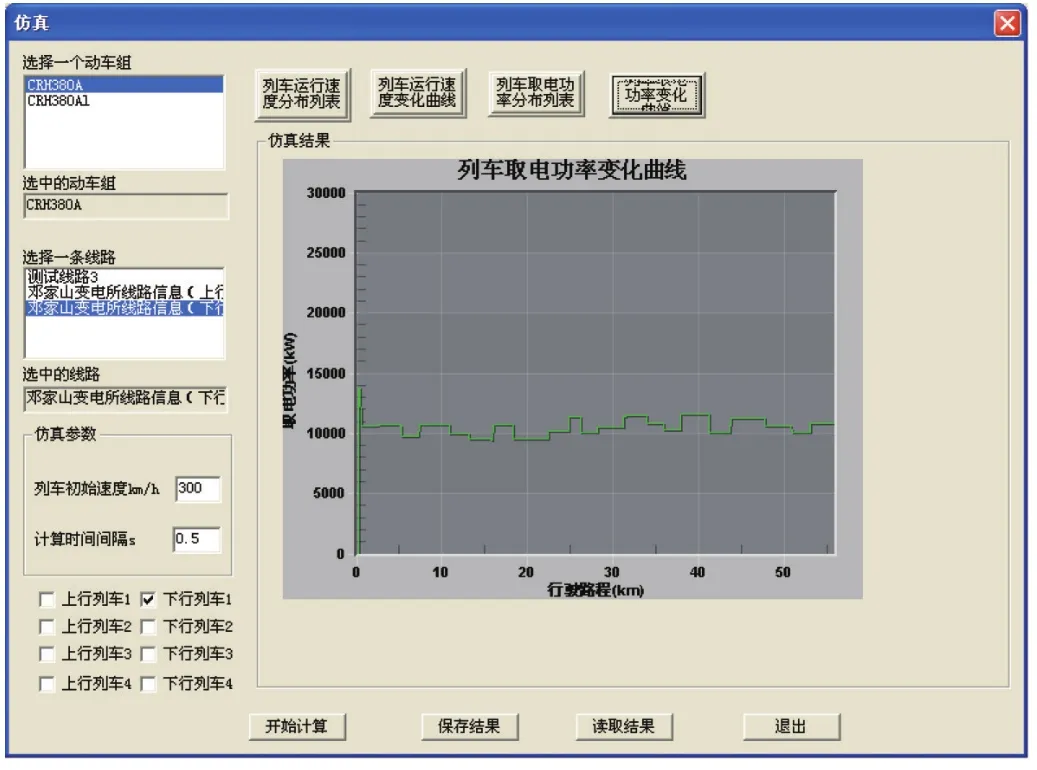
图1　牵引计算仿真结果

2　牵引供电系统的潮流计算

牵引供电系统的建模主要包括一次供电网络的建模、牵引变电所等值电路推导和牵引网的建模。

2.1　一次供电网络的建模

由于一次供电网络的系统容量远远大于牵引变电所容量。所以，采用三相戴维南等值电路，将一次供电网络简化为带内阻的理想电压源模型，如图2所示。

图2　一次供电网络等值电路

式中，ZS=Zs–Zm，即为一次系统等值阻抗。式（6）可缩写为：

2.2　牵引变电所等值电路推导

牵引变电所的等值电路实质就是牵引变压器的等值电路，由于牵引变压器区别于一般的电力变压器，它将三相电转化为两个单相电，为变电所的两侧供电臂分别供电，所以基于变压器端口电气量的一般关系和特性，建立牵引变压器通用电压变换阵N和电流变换阵M，不同的变压器接线类型和接入相序具有不同的N和M。针对高速铁路主要采用V/X接线形式牵引变压器，V/X接线牵引变压器是由两台相等容量或不等容量的二次侧中点抽出式单相变压器组合而成，V/X接线形式牵引变压器结构模型如图3所示。

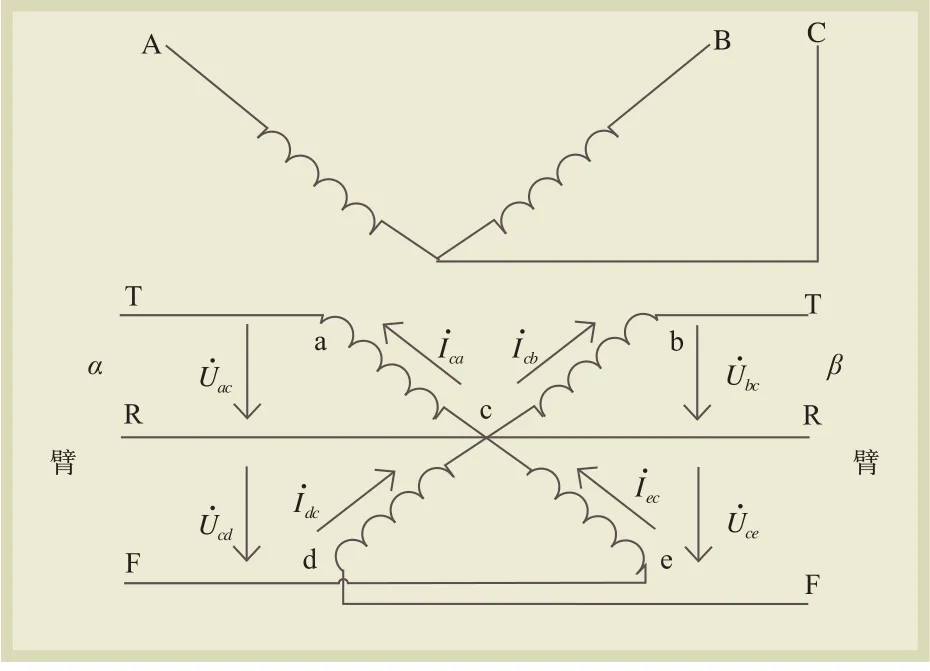
图3　V/X接线形式牵引变压器结构

根据V/X接线形式牵引变压器结构可以列出牵引变压器两边电压和电流的变换关系：

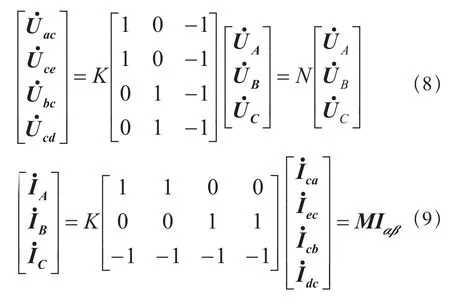
从以上两式关系可以得N和M具有以下关系：

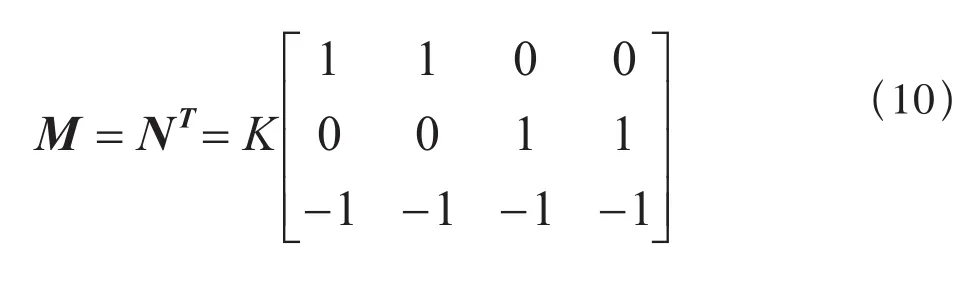
根据式（8）、式（9），可以将式（7）中一次供电网络三相电压向量EABC和阻抗矩阵ZSABC等效到牵引变电所次边为Eαβ和ZSαβ：

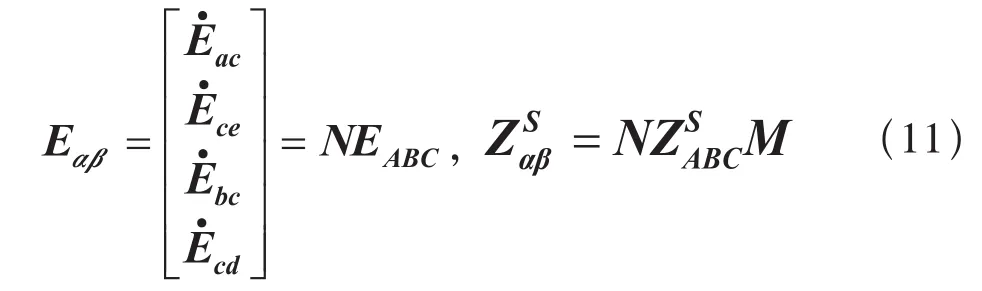
再将牵引变压器的阻抗矩阵也等效到次边为ZTαβ：

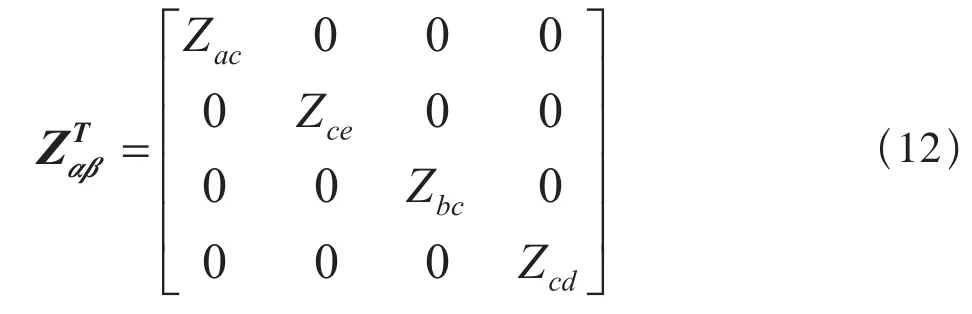
至此，将ZSαβ和ZTαβ相加即得到牵引变电所次边等效阻抗矩阵Zαβ。则牵引变电所端口电压求解的通用公式为：

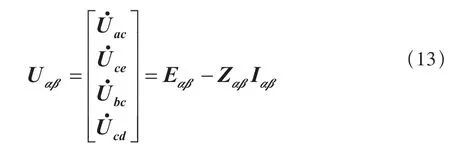
2.3　牵引网的建模

在牵引网建模方面，由于电气化铁路的牵引网是平行多导体传输线结构，所以将牵引网等效为链式网络模型，如图4所示。对牵引网按照1 km长度设置自然分段点进行切割，形成自然切面，以保留完整的牵引网电气分布特性。

图4　牵引网等效链式电路模型

由于牵引网由m根平行的导体构成，在图4中，各个切面之间的子网可表示为π型等效电路， Zi为牵引网分布阻抗矩阵，Yi为牵引网分布导纳矩阵，Ii为电力机车在切面处的负荷电流（由取电功率求得）。

根据牵引网中各导线型号及空间位置，由电磁场理论和Carson公式可以计算出牵引网分布阻抗矩阵Z为：

式中， Ci中的元素为相邻切面间各导线的自阻抗及导线间的互阻抗。

考虑到牵引网各导线间以及导线对地间存在电容效应，则牵引网的电容系数矩阵 Ci为：

式中， Ci中的元素为切面处各导线的自电位系数及导线间互电位系数的倒数，牵引网的分布导纳矩阵为Yi：

我国高速铁路的牵引网普遍采用AT供电方式，AT供电方式的牵引网导线包括：接触线、钢轨、正馈线、保护线、贯通地线，所以，对于单线铁路m为5，对于复线铁路m为10。

在计算牵引网各切面处的Yi时，还要充分考虑牵引网纵向上分布的大量横向连接所对应的并联元件的影响，这些横向连接主要包括：CPW线、横连线（全并联AT）、自耦变压器、钢轨与贯通地线的连接线，贯通地线与接地极的连接等，以及钢轨对地的泄露电导和接地极的接地电阻等。横向连接所对应的并联元件以其所对应的导纳值影响Yi中的元素值。如果并联元件出现在两个自然切面之间，则要进行分割处理，即增加一个切面。

2.4　牵引供电系统的潮流计算及负荷过程仿真

根据图4可以列出牵引网的节点电压方程为：

其中，

Y：牵引网链式模型的节点导纳矩阵，为一对角带状矩阵；

U：节点电压列向量，即牵引网链式模型各断面处的电压分布，其中，元素Ui为m维电压相量；

I：节点注入电流列向量，即牵引网链式模型各断面处的注入电流分布，其中，元素Ii为m维电流相量，用来反映运行于该断面处的电力机车从牵引网中取用的负荷电流。

通过式（11）和式（12），将一次供电网络的阻抗和牵引变压器的阻抗全都等效到牵引变电所次边，得到牵引变电所次边等效阻抗矩阵Zαβ，将一次供电网络电压源等效到牵引变电所次边，得到牵引变压器次边等效电压源Eαβ，将运行于某切面处的动车等效为恒功率模型P取电（由列车牵引计算模块得到），由P取电结合切面处当前的节点电压，计算出动车的负荷电流，将牵引网上所有动车的负荷电流求和即可得到变电所端口电流Iαβ。计算电压损失ZαβIαβ，由式（13）进而得到变电所端口电压Uαβ。根据Uαβ采用递推法即可求得各切面间牵引网的电流分布和各切面上的节点电压分布，经过反复迭代，用当前的节点电压不断地修正动车的负荷电流Iαβ，直到牵引网上各切面上的节点电压全部收敛，最后根据最终的Iαβ计算变电所内的电流分布。这样就完成一次针对动车在某一切面位置处的牵引供电系统的潮流计算。

为实现牵引供电系统的负荷过程仿真，当完成一次针对动车在某一切面位置处潮流计算后，使动车前进1 km，采用动车在新切面位置处的取电功率，重新进行一次潮流计算，如此往复直至动车驶出牵引供电系统区间。

牵引供电系统潮流计算及负荷过程仿真计算的具体计算过程如图5所示。每次的潮流计算一般迭代5～6次即可收敛，收敛精度达到10-5，满足仿真要求。

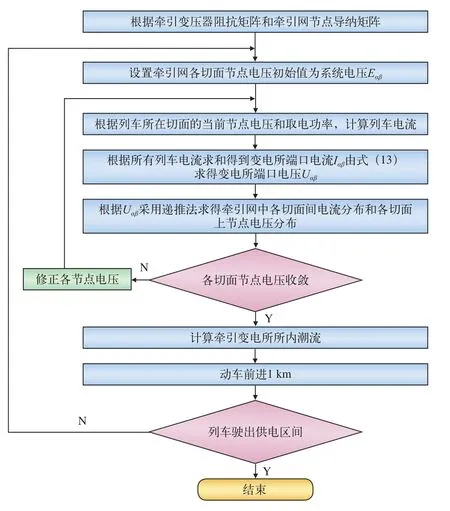
图5　牵引供电系统潮流计算及负荷过程仿真流程图

3　实例仿真

邓家山牵引变电所一次侧接入220 kV电网，一次系统的短路容量4 790 MVA，二次侧电压等级为55 kV。牵引变压器采用V/X接线形式，接入相序为BCA，变压器容量为（31.5+50）MVA，短路阻抗百分比为10.5%，AT短路阻抗为0.1+0.45 Ω，供电系统采用复线全并联AT供电方式，线路运行动车为CRH380A。图6为邓家山变电所至廖家田分区所供电区间的上行供电臂，当动车运行至23 km处的潮流仿真结果。

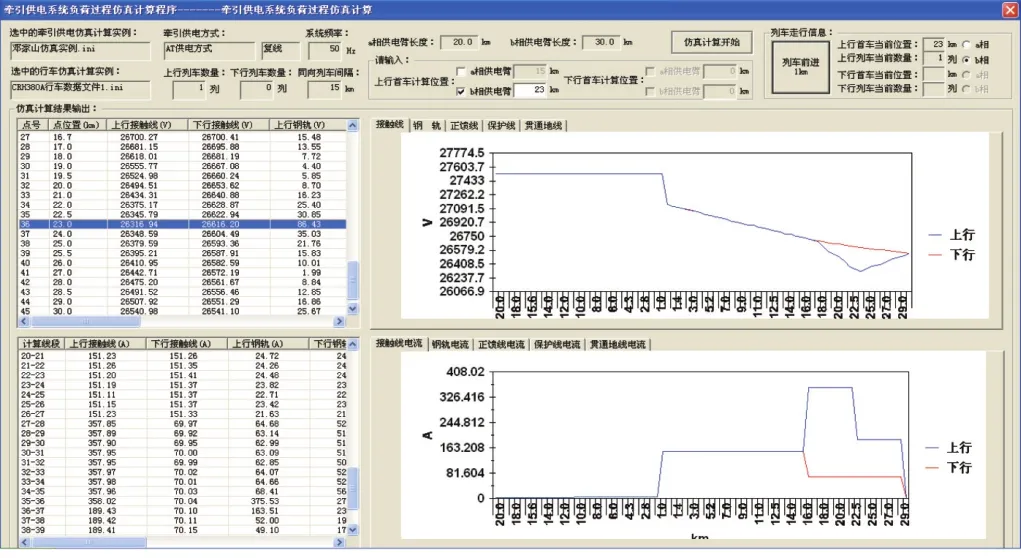
图6　牵引供电仿真计算结果

中国铁道科学研究院于2016年7月6日至7月21日选择邓家山变电所至廖家田分区所为供电测试区段，表1为动车行驶整个测试区段实测数据与通过仿真计算所得结果的对比数据，表2为上下行有车驶过曲靖北站时，曲靖北站PW线和贯通地线回流实测与仿真结果对比，表3为变电所地网回流实测与仿真对比结果，由表1对比数据可以看出仿真结果和实测数据是吻合的,说明负荷过程仿真是有效的，由表2、表3的综合接地数据对比中，仿真的轨回流占总回流的比例比实测的偏大，主要原因是在车站或变电所处接地情况较为复杂，所以地网回流较大。而且，本仿真还可以仿真变电所、AT所和分区所以外，监测不到的线路上的电压电流情况，所以本仿真对研究供电规律等方面具有重要意义。

表1　实测数据与仿真数据对比

表2　PW线和贯通地线回流实测数据与仿真数据对比

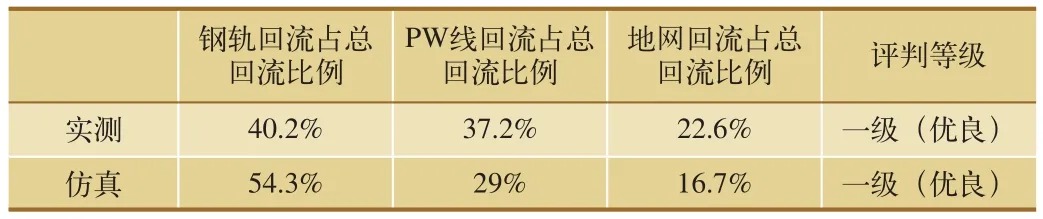
表3　变电所地网回流实测数据与仿真数据对比

4　结束语

将列车牵引计算与牵引供电系统潮流计算相结合，使供电系统负荷过程仿真计算过程更加贴近电气化铁路实际的运行情况。

将一次供电网络、V/X接线牵引变压器及牵引网各自的模型相结合，形成统一的牵引供电系统等值电路模型，以一次供电网络电压源电压为功率平衡点，结合动车的负荷功率，进行潮流计算，从而得到牵引供电系统的潮流分布。

在潮流计算基础上模拟动车行驶过程，可以动态地观察多列动车在运行过程中牵引供电系统中的电压电流变化，同时，仿真还可以监测到许多实际监测不到的地方的电压和电流，更加有利于研究供电规律。

参考文献:

[1]谭秀炳. 交流电气化铁道牵引供电系统[M]. 3版.成都:西南交通大学出版社, 2009：64-72.

[2]万庆祝.基于牵引计算的牵引变电所馈线电流仿真计算[J].电工技术学报，2007，22（6）：108-113.

[3]何俊文.交流牵引供电系统仿真通用数学模型及其应用[J].电网技术：2010，34（7）：25-29.

[4]Goodman C J,Kulworawanichpong T. Sequential linear power fl owsolution for AC electric railway power supply systems[J].Computersin Railways VIII:2002,61(13):531-540.

[5]李群湛，贺建闽．牵引供电系统分析[M]．成都：西南交通大学出版社，2007：81-85．

[6]吴命利.牵引供电系统电气参数与数学模型研究 [D].北京：北京交通大学，2006.

[7]王 芳，王晓茹.基于恒功率负荷的牵引供电系统潮流计算[J].电力系统及其自动化学报，2105，27（3）：59-64.

[8]何正友.基于AT等值电路的牵引网潮流计算方法[J].西南交通大学学报：2008，43（2）：1-6.

[9]吴命利.电气化铁道牵引网的统一链式电路模型[J].中国电机工程学报，2010，30（28）：52-55.

[10]辛成山．AT 供电系统等值电路推导方法［J］.电气化铁道，1999（1）： 17-20

[11]马庆安.高速铁路AT供电若干问题的研究[D]. 成都：西南交通大学，2013

[12]赵 滕.高速铁路全并联牵引网供电特性研究[D].北京：北京交通大学，2012.