数控激光切割机伺服进给系统的机电耦合建模与仿真分析
刘 冲,王金荣,涂芬芬,王万杰,周 祥
(江苏省金属板材智能装备重点实验室,江苏 扬州 225200)
伺服进给系统是一种典型的复杂机电系统,输出的进给位移、速度和加速度一方面会影响机械系统的动态特性,另一方面也会影响伺服系统的动态特性,而伺服输出力特性的变化作用到机械环节,又会影响系统的动态特性[1]。进给系统的运动精度与伺服驱动输出特性、机械执行系统动态特性以及两者的相互作用关系密切相关[2]。
在不同工况下,激光切割机的不同数控轴和运动部件对速度、加速度和精度等具有不同的要求[3]。例如,切割头的随动控制则要求与数控轴控制之间进行柔顺的控制过程切换,保证随动速度快而无过冲现象。因此,有必要研究数控系统、运动控制系统、伺服驱动系统、机械运动部件之间的机电耦合关系。本文以江苏亚威某型激光切割机的X轴系统为研究对象,建立了该系统的机电耦合模型,并仿真分析了系统传动刚度对伺服系统的影响。
1 激光切割机伺服进给系统模型

图1 伺服进给系统组成图
伺服进给系统包含控制器、驱动器、交流永磁同步电机、联轴器、滚珠丝杠、导轨、滑枕、滑块和反馈元件等,如图1所示。其工作原理为控制器控制电机输出力矩大小,然后电机将输出力矩作用在滚珠丝杠上,丝杠在驱动力矩的作用下产生加速度,进而发生转动,通过螺母的运动耦合作用,驱动滑枕的进给运动[6]。同时滑枕的进给位移、速度以及电动机转速等机械系统状态变量均通过传感器反馈给控制系统,控制系统根据输入指令和系统状态变量等对伺服电机的力矩输出指令进行调节,以达到跟踪输入指令的目的。
伺服进给系统的机电耦合方式主要为三类:第一类是电磁场产生的谐波分量对传动系统的振动构成直接激励,对系统的主运动产生扰动;第二类是控制变量与主体运动的力学参数构成参数弱变量耦合形式,如电枢回路中的谐波电流经反馈回路进入控制系统中,通过驱动系统的功率放大后,再作用于机械主运动,对其产生影响;第三类是外负载耦合影响主运动。可见,数控系统的运动控制指令、伺服驱动系统的电气参数变化、外负载的波动均会通过机电耦合方式影响数控机床[7],如图2所示。

图2 伺服进给系统的机电耦合
2 机电耦合建模
2.1 机械传动系统
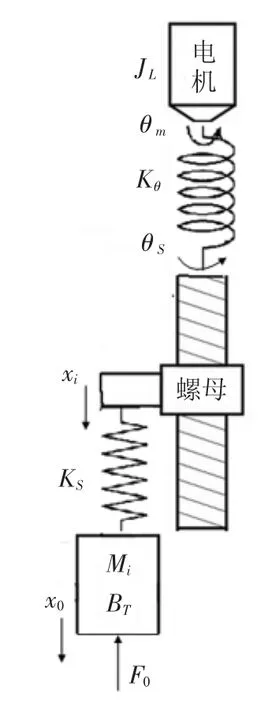
图3 机械系统组成及参数
由于联轴器和丝杠都是弹性体,因而传动系统中存在扭转变形和拉压变形,因此将主轴伺服进给系统机械传动部分简化为图3所示的等效动力学模型。其中 JL,CL,分别为系统中转动部件总的转动惯量和转动阻尼系数;MT,BT分别为系统中移动部件(滑枕)的总质量和滑动导轨上的粘性阻尼系数。Kθ,Ks分别为机械传动系统总的扭转刚度和总的轴向刚度;F0为摩擦力和切削力。xi为螺母的轴向位移,x0为滑枕的轴向位移。
首先伺服电机驱动转矩经过刚性联轴器联接转化为滚珠丝杠的旋转运动,忽略电机与丝杠间的转角偏差,则电机和丝杠的旋转运动间存在如下的动力学关系:

根据能量守恒定理,可知负载转矩与驱动力FL之间的关系如下:

式中:TL——折算到丝杠轴上的负载转矩;
θm、TM——分别为电机输出转角和扭矩;
Ls——丝杠导程;
η——丝杠传动效率。
丝杠螺母将滚珠丝杠的旋转运动转换为滑枕的直线运动,则滑枕的动力学关系如下:

式中,驱动力FL可通过机械传动系统的综合等效刚度和机械传动系统的轴向变形由下式计算:

K——机械传动系统的综合等效刚度,其计算公式如下:

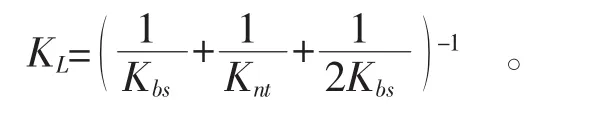
其中:Kθ、KL——分别为机械传动系统的扭转刚度和轴向拉压刚度;
Kcθ、Ksθ——分别为联轴器、丝杠扭转刚度;
Kbs、Knt、Ksb——分别为丝杠轴拉压刚度、丝杠螺母接触刚度、支承轴向刚度。其数值可查阅相关资料计算得到。
2.2 永磁交流同步电机
伺服驱动系统常采用永磁同步电机(PMSM)作为执行元件[8]。在定子结构上,铁心直接与外界空间接触,散热情况良好,易于实现小型化和轻量化。在转子结构上,用永磁体取代电励磁,取消了励磁线圈、滑环和电刷,无需额外的直流励磁电路,提高了电机的效率和功率密度。由于没有励磁损耗,电机的发热只取决于电枢电流。永磁稀土材料具有很高的剩余磁通密度和很大的矫顽力,可显著减少电枢反应。然而,永磁同步电机的多变量动态数学模型结构复杂,分析求解困难,在实际应用中通常设法将其简化。
直流电机的数学模型比较简单,若将PMSM的物理模型等效变换为直流电机的模型,则分析和控制将大为简化。因此采用clark和park变换将PMSM在ABC坐标系下的数学模型等效变换为d-q坐标系下的数学模型,并对电机做出如下假设:(1)忽略磁路饱和;(2)电动机气隙磁场均匀分布,感应反电势呈正弦波状;(3)忽略磁滞及涡流损耗。采用矢量控制策略id=0的控制方式,则可得永磁同步电机的电压方程式、电磁转矩方程和转矩运动平衡方程分别如下所示:


2.3 伺服控制系统
全闭环伺服驱动系统可分为位置控制器、速度控制器、功率放大器和伺服电机,如图4所示。伺服驱动系统完成位置、速度、力矩的三闭环控制,并通过伺服电机带动传动机构使执行元件完成规定的目的运动。伺服电机上安装的电流传感器和速度传感器分别把电流信号、速度信号反馈给功率放大器和速度控制器。执行元件上安装的位置传感器分别把位置信号反馈给位置控制器和数控系统。
在位置环,位置误差为:

位置环控制器通常采用比例控制,则输出信号为:

式中:Xr为参考位置;K1为位置环比例系数。
在速度环,速度误差为:

速度环控制器通常采用比例积分控制,则输出信号为:

式中:K2为速度环比例系数;T2为速度环积分时间常数。
在电流环,电流误差为:

电流环控制器通常采用比例积分控制,则输出信号为:

式中:K3为电流环比例系数;T2为电流环积分时间常数。
综合式(1)~式(14),可得伺服进给系统的机电耦合数学模型,其系统控制结构框图如图5所示。
根据系统结构控制图应用Matlab/Simulink建立了系统的仿真模型,如图6所示。
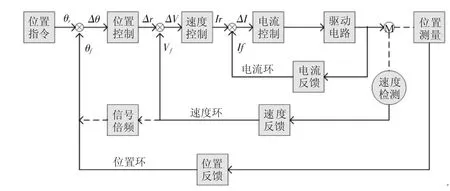
图4 全闭环伺服驱动系统
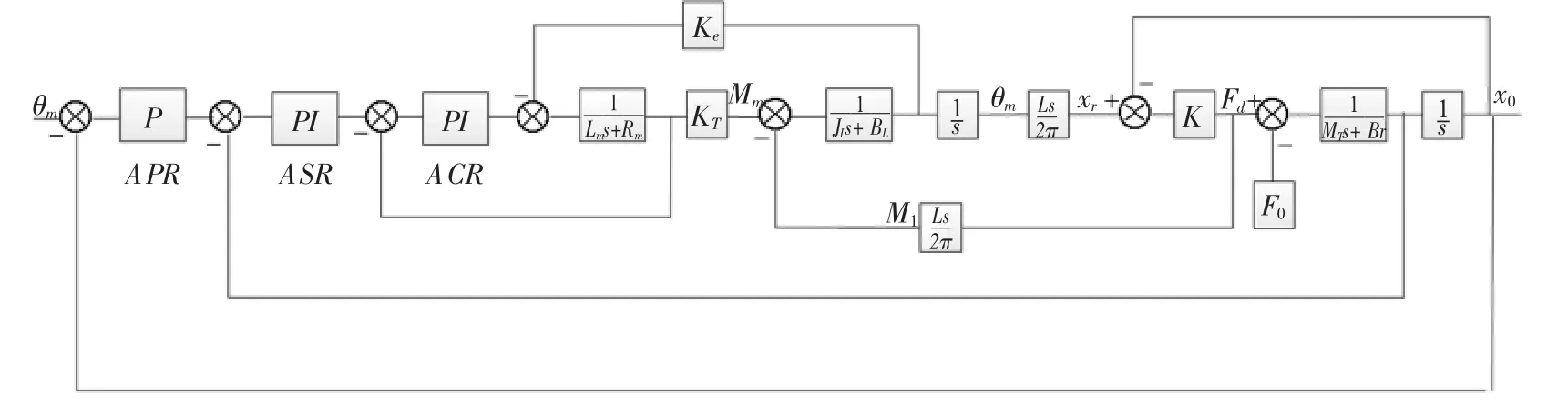
图5 伺服进给系统的控制结构图
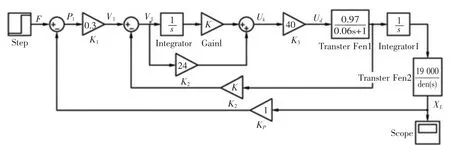
图6 Simulink仿真模型
3 传动结合面刚度与整体传动刚度变化对伺服系统的影响分析
在机床高加速下由于运动部件的惯性力使结合部的负载发生变化,进而导致结合部刚度发生变化或突变,出现变异。根据丝杠的具体型号,查阅手册可得到其轴向的额定动载荷(或预紧载荷),在螺母副不受负载的情况下,可得到每个滚子的法向力为:
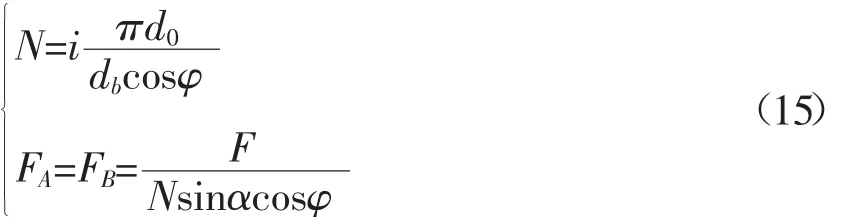
式中:d0为丝杠的公称直径;db为滚球的直径;α滚球与滚道的接触角;φ为丝杠的螺纹升角;i为单螺母总的承载圈数;N为承载的滚子个数;F为双螺母的预紧载荷;FA、FB为滚子的法向力。
由赫兹接触理论和双螺母丝杠预紧结构,对每个滚子进行受力分析,并利用刚度定义,便可得到丝杠螺母副的轴向接触刚度。
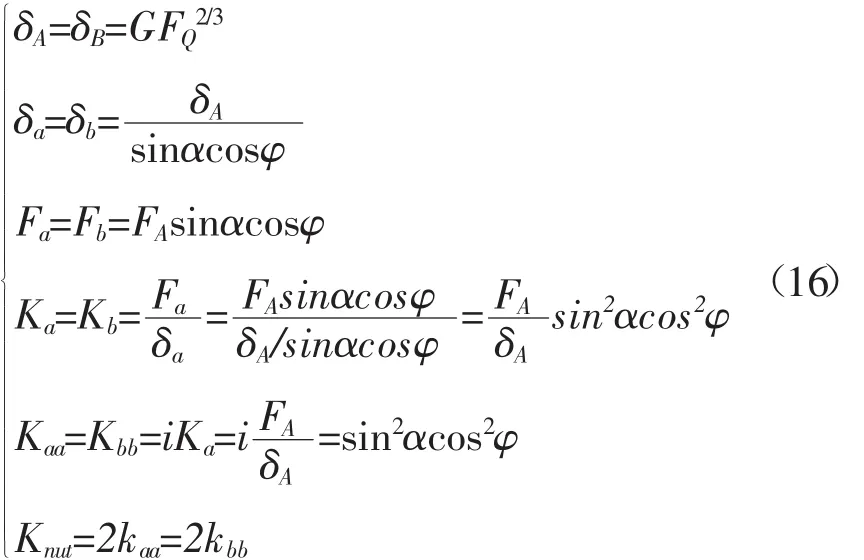
式中:FA、FB、δA、δB为螺母副 A、B 滚子的法向力与变形量;FQ为两个接触对象之间作用力;G为柔度系数;Fa、Fb、δa、δb为螺母副 A、B 滚子的等效进给力与变形量;Ka、Kb为螺母副A、B中单个滚子的等效轴向刚度;Kaa、kbb为螺母副A、B的等效轴向刚度;Knut为丝杠螺母副的等效轴向刚度。
图7为常用的双螺母丝杠驱动结构,设质量m的负载在丝杠螺母副的驱动下,以加速度a向右运行,则惯性力向左,大小为ma,设此惯性力对每个滚子的作用力为Fq,对于螺母A而言,则受力FA=F+Fq,而螺母B受力为FA=F-Fq。下面讨论螺母B的受力状态。

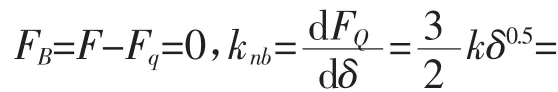
(3)当 F<Fq时,则 FB=F-Fq=0,此时出现间隙,刚度出现突变。
结合实际应用,选取轴承预紧力矩为20N·m,螺母副额定动载荷分两种情况:3000×9.8N和5220×9.8N,负载质量也分两种情况:216kg和432kg。利用经典赫兹接触理论对螺母副的轴向刚度和加速度振动响应进行仿真分析计算,结果如图7和8所示。从图9可知,在不同的加速度下,丝杠螺母副的轴向刚度会发生变异;在螺母副的额定动载荷一定时,运动负载越大,其轴向刚度变异点的加速度越小;当运动负载一定时,其轴向刚度变异点的加速度随螺母副额定动载荷的增大而增大。
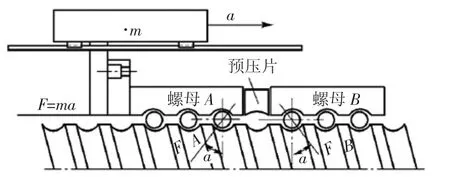
图7 丝杠螺母副内部滚子的受力图
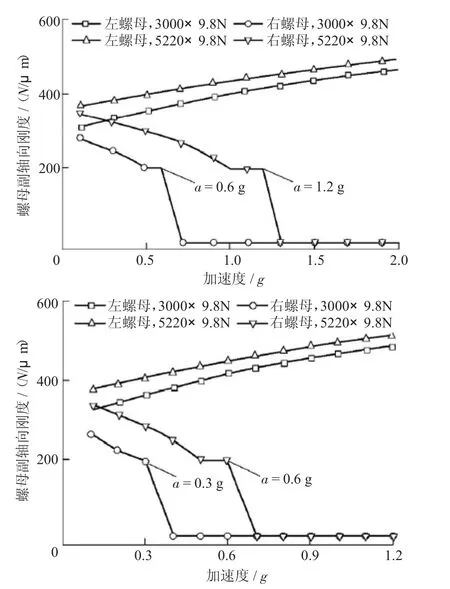
图8 螺母副轴向刚度

图9 加速度振动响应
当螺母副的额定动载荷为3000×9.8N,轴承预紧力矩为20N·m时,不同质量下该系统的进给方向的加速度振动响应如图9所示。由图可知,进给系统的加速度振动响应在不同的加速度下会发生变异;变异点处的固有频率与加速度振动幅值都有明显的变化;不同运动负载也会影响到进给系统进给方向加速度振动响应的变异点;运动负载较大下进给系统进给方向的加速度振动幅值较运动负载较小的幅值低。
改变传动刚度分析伺服系统的响应发现:刚度越低,传动部件的变形越大;系统的刚度越大,固有频率越高,对系统的稳定性有利。从图10中可以看出,刚度减少时,系统调节时间变长,响应速度变慢,启动时有着明显的抖动现象。
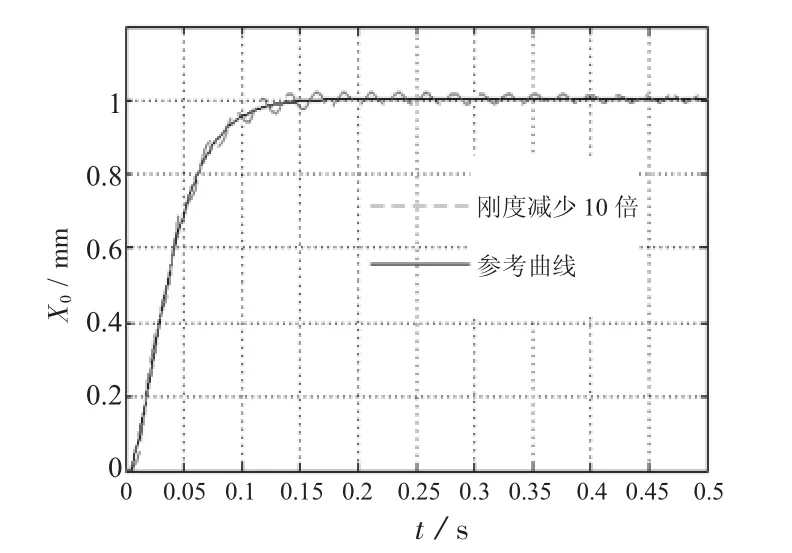
图10 刚度变化的影响
4 结论
(1)通过分析激光切割机伺服进给系统的机电耦合关系,以系统各个环节为研究对象,建立了伺服系统的机电耦合模型;
(2)运用Matlab/Simulink对该模型进行了仿真,分析了传动刚度对伺服系统动态性能的影响。受结合面刚度非线性的影响,机械系统的质量分布会随着位置的不同发生偏移;丝杠螺母副以及轴承副的轴向刚度随着加速度的不同而不同,并且随着加速度的增大,存在刚度突变点,相应的额定动载荷和负载质量都会影响加速度对机械系统的影响。在高速高加速度下,机械系统的以上时变特性变得更加显著。整体传动刚度的变化会直接影响系统响应,传动刚度越大越有利于系统稳定;
(3)利用系统的机电耦合模型,可快速对系统伺服参数进行优化,提升伺服进给系统的设计效率。
[1] 宋 玉,陈国鼎,马术文.交流伺服进给系统数学模型研究及其仿真[J].机械,2010,(7):9-12.
[2] 韦富基,谭顺学.高精度数控机床伺服进给系统精度研究[J].制造业自动化,2012,(9):69-71.
[3] 胡金龙,周鹏飞,翟东升,等.数控激光切割机传动系统的研究[J].锻压装备与制造技术,2012,(1):22-25.
[4] 吕 浪,熊万里,侯志泉.面向机电耦合振动抑制的电主轴系统匹配特性研究[J].机械工程学报,2012,(9):144-154.
[5] 胡 秋.数控机床伺服进给系统的设计 [J].机床与液压,2004,(6):55-56,74.
[6] 林利红,陈小安,周超群,等.精密传动系统的机电耦合建模及仿真分析[J].重庆大学学报,2007,(11):14-18.
[7] 孟 杰,陈小安,合 烨.高速电主轴电动机--主轴系统的机电耦合动力学建模[J].机械工程学报,2007,(12):160-165.
[8] 薛 青,花银群,程广贵,等.基于永磁同步电机的高性能交流伺服控制系统研究[J].科学技术与工程,2009,(1):29-33.

