Pushover方法在钢管混凝土拱桥抗震分析中应用

申现龙， 陈永祁， 刘 荷， 郑久建， 张海江

(1.燕山大学 建筑工程与力学学院，河北 秦皇岛 066004；2. 北京奇太振控科技发展有限公司，北京 100037)

传统抗震设计是基于承载能力极限状态为准则，而基于性能抗震设计是在不同水准的地震作用下，所设计的结构能够满足各种预定性能目标下的要求。而具体性能要求应根据相应的地震设防水准来确定。基于性能抗震设计的分析方法主要有非线性静力分析(Pushover)和非线性时程分析(NL-THA)方法。NL-THA可以考虑地震动输入后的整个结构屈服及破坏过程，发现结构薄弱环节出现顺序，被公认为对结构非线性分析最有效的方法。但该方法计算非常耗时，且有输入输出比较繁琐等缺点。在结构初步设计阶段就采用NL-THA方法显然不现实，因此，对结构初步设计的抗 震性能评估，Pushover分析方法就体现出了所具有的简化计算和提高分析效率等优点，在近些年来得到各国学者的推崇。

19世纪70年代初，美国学者Freeman等[1]首次提出能力谱法并完成一个结构抗震评估项目后，传统Pushover分析(Standard Pushover Andlysis,SPA)方法引起了世界各国研究人员的重视。Chopra等[2-3]提出考虑高阶模态影响的模态Pushover方法(Modal Pushover Analysis,MPA)，介绍了MPA基本步骤并对规则和非规则建筑进行地震需求评估。Jan等[4]提出另一种考虑高阶模态影响的上界Pushover方法(Upper Boundary Pushover Analysis,UBPA)，认为结构动力反应主要由前两阶模态控制，考虑第二模态对侧向力及目标位移的贡献。Poursha等[5]将其拓展到非规则建筑并得到较准确的地震需求评估。以上方法都是基于建筑结构中的应用研究，而对桥梁结构的研究仍相对较少。Paraskeva等[6]将MPA方法应用于桥梁结构，提出了基本分析步骤并以弯桥横向地震需求评估为例，得出MPA方法评估较SPA方法更为准确。魏标等[7-9]对MPA方法在桥梁结构进行了适应性探索，仍未发现有关UBPA方法应用在桥梁结构上的相关文献。

目前国内学者运用Pushover方法对桥梁整体结构或桥墩构件的能力评估，极少有关在地震作用下对桥梁整体结构的地震需求评估。本文主要侧重MPA和UBPA方法在CFST拱桥地震需求评估中的应用。以实际工程景洪大桥为例，以NL-THA方法为标准对比，验证了Pushover方法用于CFST拱桥纵向地震需求评估的可行性。

1 侧向荷载模式

侧向荷载分布对结构地震需求评估起到重要的作用[10]。只有选取合理的侧向荷载，才能真实地反映地震作用下结构质点惯性力的分布特性，所求的响应才能真实反映地震作用下结构的性能表现。固定侧向荷载模式至少采用二种以上[11]。本文在SPA、MPA和UBPA方法中各采用了的四种侧向力分布模式。

常加速度荷载模式(记作SPA-M)，节点侧向力与相应节点质量成正比。即荷载向量为。

fs=ma

(1)

第一阶模态形状侧向力模式(记作SPA-φ1)，相应节点侧向力与第一阶模态形状成正比。即荷载向量为

fs=φ1

(2)

MPA侧向力模式(记作MPA)，前四阶模态侧向力分别加载，各阶模态相应节点力与前四阶模态形状和相应节点质量乘积成正比。即荷载向量为

(3)

UBPA侧向力模式(记作UBPA)，通过第二模态对目标位移的贡献来确定第二模态侧向力模式的贡献率，以考虑第二模态贡献率的第一模态侧向力分布。即荷载向量为

(4)

(5)

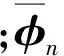
2 实例分析

2.1 工程概况

景洪大桥位于景洪市市区上游1.4 km处，其主桥长为353.5 m，桥跨布置为(70+200+70)m。桥型为下承式CFST(Concrete-Filled Steel Tube)拱加劲连续刚构拱桥，立面图如图1。梁体截面类型为单箱单室直腹板变截面箱梁，除零号段外，各段梁底下缘按二次抛物线y=4.5+x2/921.655(m)变化。拱肋计算跨度L=200 m，矢高f=40 m，矢跨比f/L=1∶5，其截面形式为哑铃型见图。拱轴线采用二次抛物线，设计拱轴线方程为y=x2/250+0.8x。全桥共设19组吊杆，顺桥向间距9 m。主墩采用实腹轨道型截面见图3，最大墩高27 m，承台高4.5 m。主墩基础均为钻孔群桩，桩径2.2 m，每个墩柱下共12根成行列式布置。

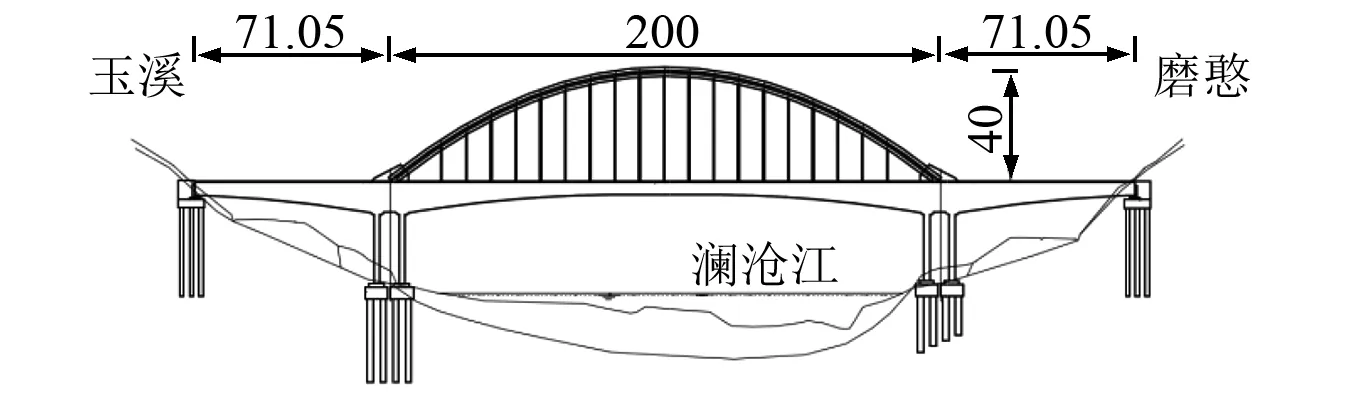
图1 景洪大桥总体立面图(单位：mm)Fig.1 Jinghong bridge overall elevation(unit:mm)

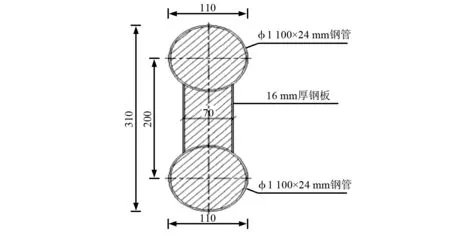
图2 拱肋截面尺寸(单位：cm)Fig.2 Sectional dimension of arch rib(unit:cm)

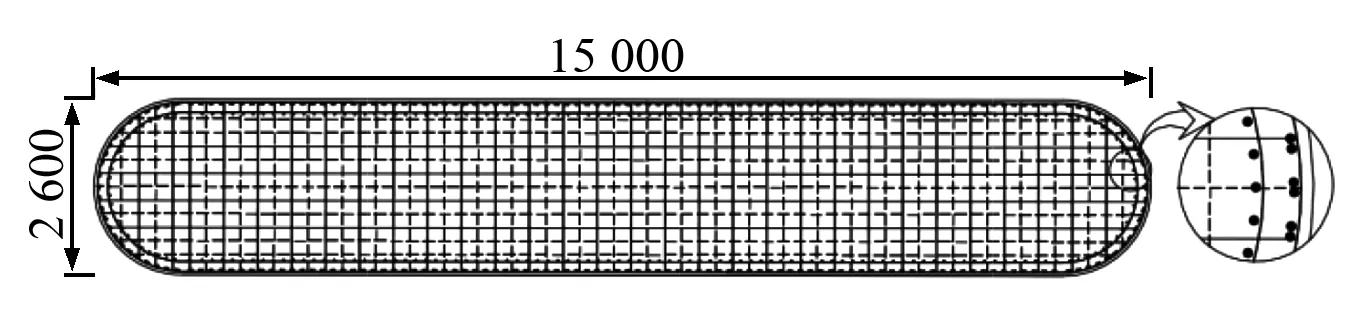
图3 桥墩配筋图(单位：mm)Fig.3 Reinforcement of piers(unit:mm)

2.2 模型建立

采用Midas有限元软件建模，模型如图4。主梁、拱肋、桥墩和基础采用一般梁单元。拱肋采用换算截面法，将钢管混凝土复合材料根据刚度等效原则简化为混凝土材料，钢管Q345与混凝土C50的弹性模量比和重度比分别为5.8和3.08，采用Midas自带截面特性计算器功能计算截面特性值并导入到模型。吊杆采用只受拉桁架单元，并施加初始拉力。桩基础以门形刚架模型[12]来模拟墩-土相互作用，等效门形刚架主要特性参数见表1。根据铁路工程抗震设计规范，在罕遇地震作用下，桥墩可以进入塑性状态，桥梁其他构件不考虑塑性。桥墩材料采用C35混凝土，主筋采用HRB400，桥墩截面配筋率为1.79%。单元非弹性铰特性采用集中铰骨架曲线，作用类型采用轴向力与弯矩相互作用的P-M屈服面，P-M及M-M相关关系的公式模拟三维屈服面见图5，参数γ、β和α取值分别为1.1、2和1.4。钢筋混凝土的滞回模型采用武田三折线见图6，三折线模型的第一和第二刚度折减率为0.1和0.05，卸载刚度的幂阶取0.4，轴力及双向弯矩的第一和第二屈服强度及变形由程序自动计算[13]。

桥梁的连接条件是拱肋与主梁刚性连接，主梁与主墩刚性连接，边跨纵向活动支座以刚性连接竖向和横向固定模拟。对结构进行非线性时程分析时，结构体系的阻尼采用Rayleigh阻尼,结构的纵向第一振型和第二振型所对应的振型阻尼比为5%。

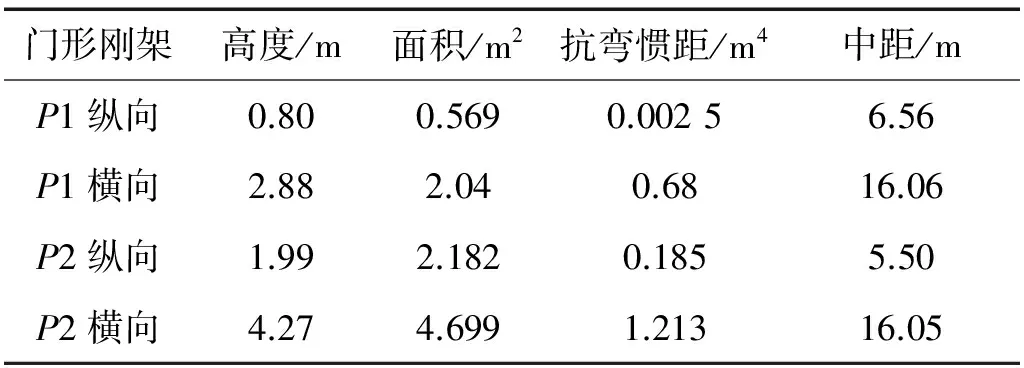
表1 门形刚架主要特性参数

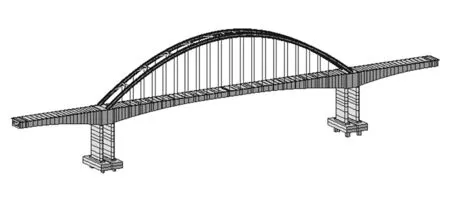
图4 景洪大桥三维有限元模型Fig.4 Three-dimensional finite element model of jinghong bridge

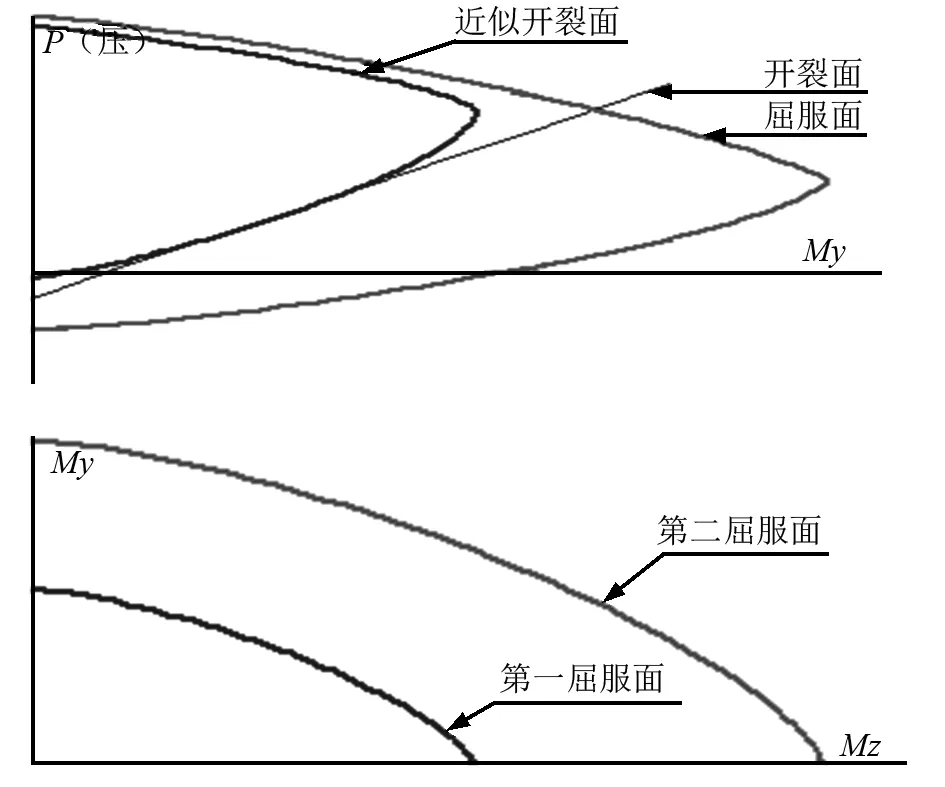
图5 P-M相关曲线及屈服面Fig.5 P-M correlation curve and yield surface

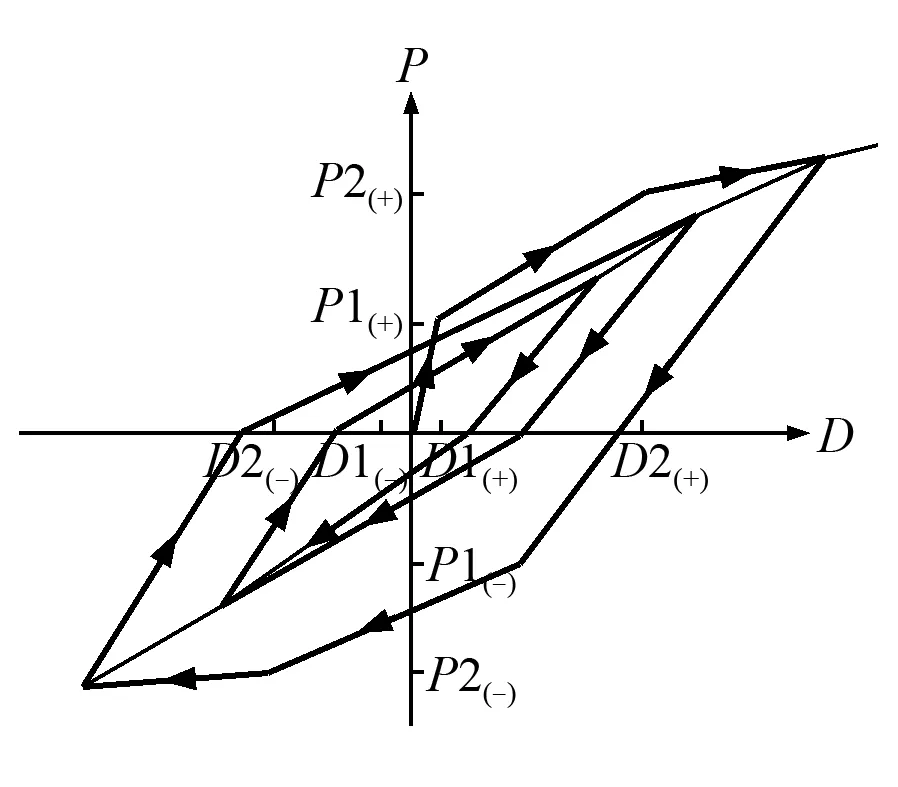
图6 武田滞回模型Fig.6 Takeda hysteresis model

2.3 结构纵向自振特性分析

在进行Pushover分析前，本文采用多重Ritz向量法估算了该桥的结构自振特性。该桥取前70阶振型时，x(顺桥向)、y(横桥向)、z(竖向)方向振型参与质量达到99.6%以上。由于本文仅对结构顺桥向进行Pushover分析，给出顺桥向振型参与质量大于1%的前4阶模态见表2，顺桥向前4阶振型参与质量总和为89%。顺桥向4阶模态形状如图7所示。

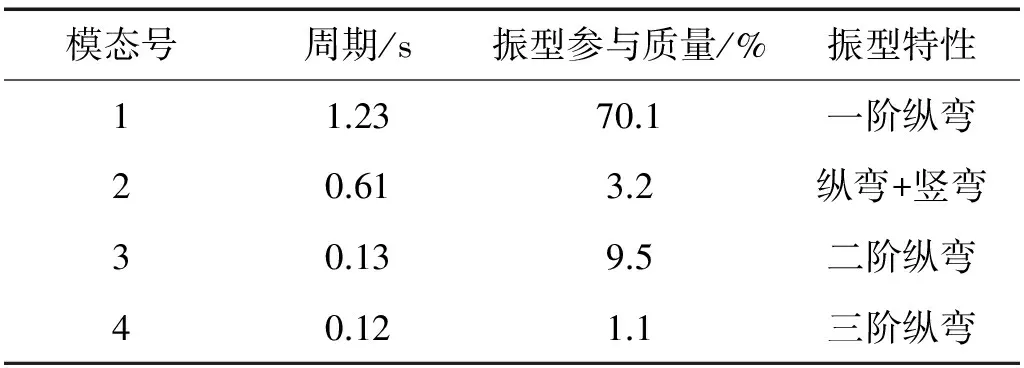
表2 结构纵向自振特性参数

图7 结构模态形状Fig.7 Structural modal shape

2.4 地震动输入

安全性评价报告提供的该桥罕遇地震(100年超越概率3%)抗震设防水准目标反应谱，其特征周期为0.55 s。采用SIMQKW[14]随机生成与目标反应谱对应的3条人工地震波见图8(a)，其峰值加速度为0.504g，地震动持续时间为40 s。3条地震波伪加速度反应谱与目标反应谱对比见图8(b)。由图可见，人工地震波与目标反应谱拟合较好，有效反应场地预定超越概率下的地震动水平。

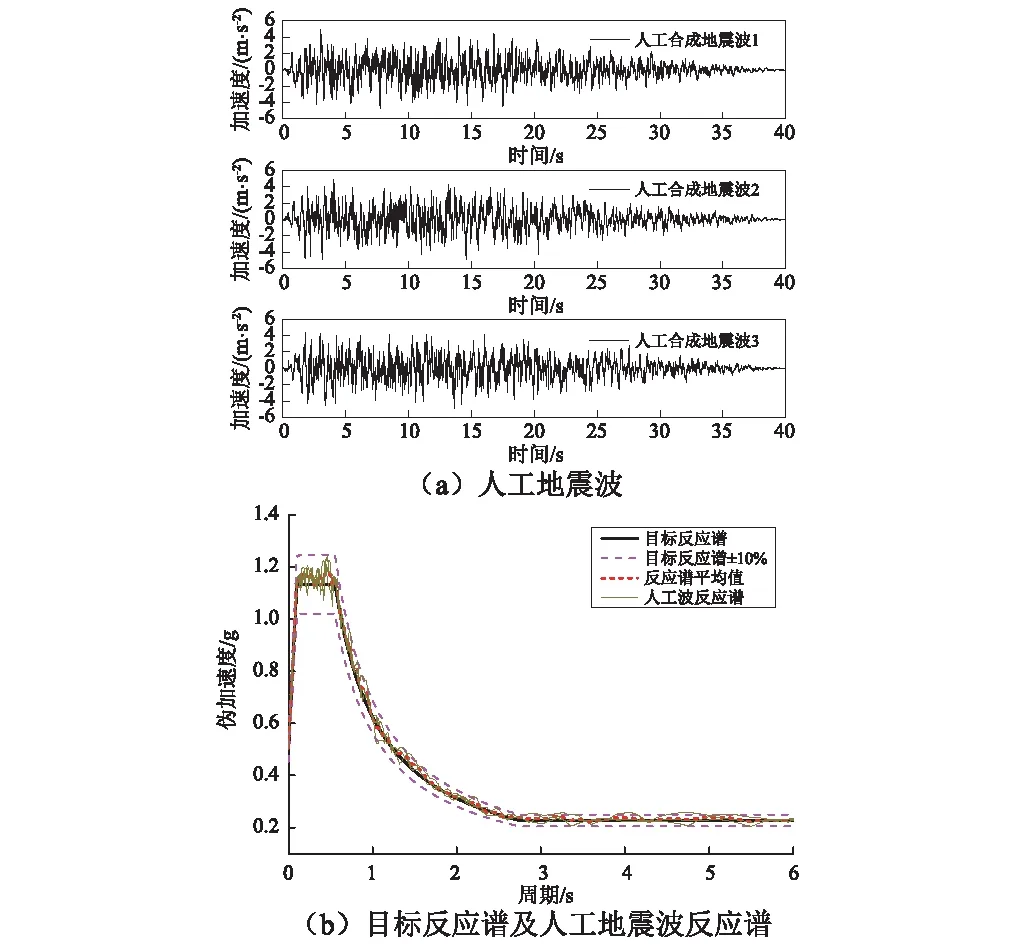
图8 地震动输入地震波及拟合反应谱Fig.8 Input seismic wave and fitting response spectrum

3 结果分析

在进行Pushover前，先考虑桥梁成桥状态下静力荷载对结构的影响，再根据上文四种不同分布力模式分别对桥梁进行Pushover分析，采用基于目标位移的位移控制法。结构整体能力曲线一般定义为结构的基底剪力与顶部水平位移的关系曲线。能力曲线取决于控制点选取，本文以主梁的中心节点为控制点[15]。获得结构能力曲线后，再将其转化为等效单自由度能力谱曲线。采用能力谱方法[16]计算等效单自由度的等效阻尼比，把弹性地震需求谱折减为非弹性地震需求谱。最后，用等效单自由度能力谱曲线与弹塑性地震需求谱来确定控制点的地震需求。MPA方法通过前4阶模态侧向力来获得各控制点峰值位移，再采用随机理论的SRSS组合规则求得桥梁结构的总的需求位移。UBPA方法考虑第二阶模态对控制点位移的贡献求得桥梁结构的总的需求位移。

3.1 桥梁整体结构能力评估

图9和图10分别为不同Pushover方法的整体能力曲线的比较和伪加速度与模态位移反应谱ADSP(Acceleration-Displacement Response Spectra)曲线。从图9可以看出，在控制点最大位移为0.3 m的范围内，不同侧向力模式(除了mode3和mode4侧向力模式)作用下，桥墩均明显进入塑性状态，并且屈服位移接近于0.06 m。由于前四种侧向力模式求得的能力曲线并不一定代表桥梁所有构件的实际响应，如当施加mode3和mode4侧向力时，桥梁结构不会很快进入非弹性状态。在相同位移需求下，不同的侧向力模式对桥梁的非弹性反应影响会有较大不同。当分别施加SPA-M、mode2、UBPA、mode1和SPA-φ1侧向力时，结构的基底剪力逐渐减小。由于SPA-φ1侧向力模式对应的最大位移出现在P1墩顶，墩底剪力仅在P1墩处较高，而SPA-M侧向力模式，在所有桥墩墩底处产生剪力大致相同。因此，在相同的位移需求下，最大基底剪力发生在SPA-M侧向力模式情况。

从图10可以看出，将基地剪力-监控点位移(V-u)转换谱加速度和位谱位移(Sa-D)曲线后，侧向力mode2、mode3和mode4在地震需求谱下结构并没有进入非线性，由于高阶模态参与系数和等效模态质量较小。通过SPA-φ1和SPA-M侧向力模式求得的等效单自由度能力曲线与以等效阻尼比为12%折减后的非弹性需求谱的交点，确定结构的控制点地震需求位移分别为0.212 m和0.178 m。同样可求得在mode 1侧向力模式下结构控制点地震需求位移为0.212 m，在高阶模态(mode2、mode3和mode4)侧向力作用下，求得等效单自由度能力曲线与以5%结构阻尼比的弹性需求谱的交点，确定结构控制点地震需求位移分别0.015 m、0.006 m和0.002 m。MPA通过采用SRSS组合规则求得的控制点地震需求位移，从而得到控制点地震需求位移峰值为0.213 m。UBPA通过第二阶模态对控制点地震需求位移的贡献，采用公式ur=u1×[1+(Γ2·D2/Γ1·D1)]，求得控制点地震需求位移为0.215 m。

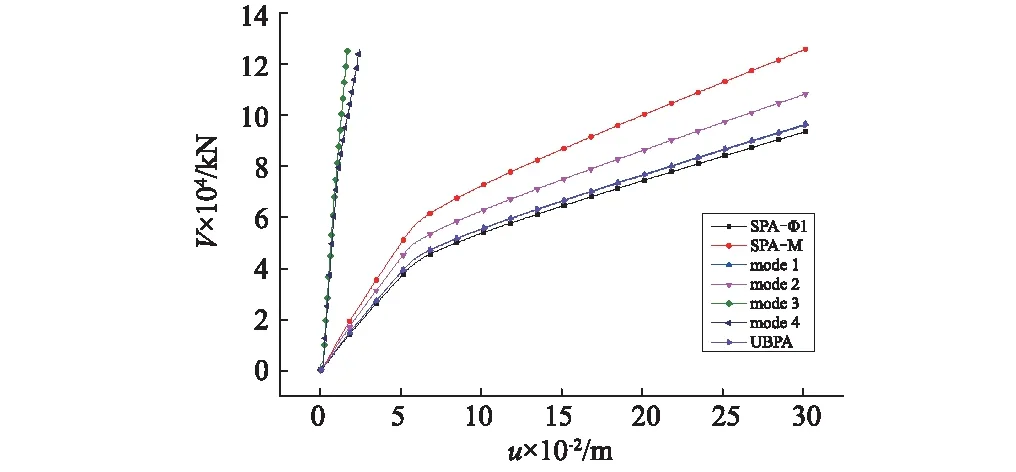
图9 基底剪力与控制点位移关系Fig.9 Relationship between base shear and displacement at control point

3.2 控制点位移

四种Pushover方法和NL-THA方法求得该桥关键位置控制节点位移及误差见图11。其中误差定义为|1-RPushover/RNL-THA|×100%，RPushover为Pushover方法的响应值，RNL-THA为非线性时程积分方法的响应值。下文所有误差都采用此公式表示。用UBPA方法求得桥墩顶和梁端控制点的位移几乎与NL-THA方法一致，误差最大为1.8%，对拱顶位移略微偏高，误差在3.46%。MPA方法求得桥墩顶和拱顶位移几乎与NL-THA方法一致，最大误差为1.9%，而梁端位移误差到6%。SPA-φ1方法对拱顶位移最大误差到达12.55%，而SPA-M方法对控制点的最大误差为23.81%。MPA方法对梁端位移高估，这是由于没有考虑模态塑性发展过程中的刚度矩阵变化，因而采用SRSS组合规则对梁端位移引入误差。通过拱顶位移比较看出，高阶的模态对拱顶位移的贡献起到重要的作用。

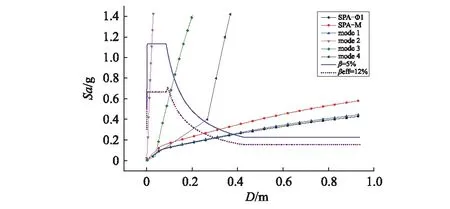
图10 ADRS曲线Fig.10 ADRS curve

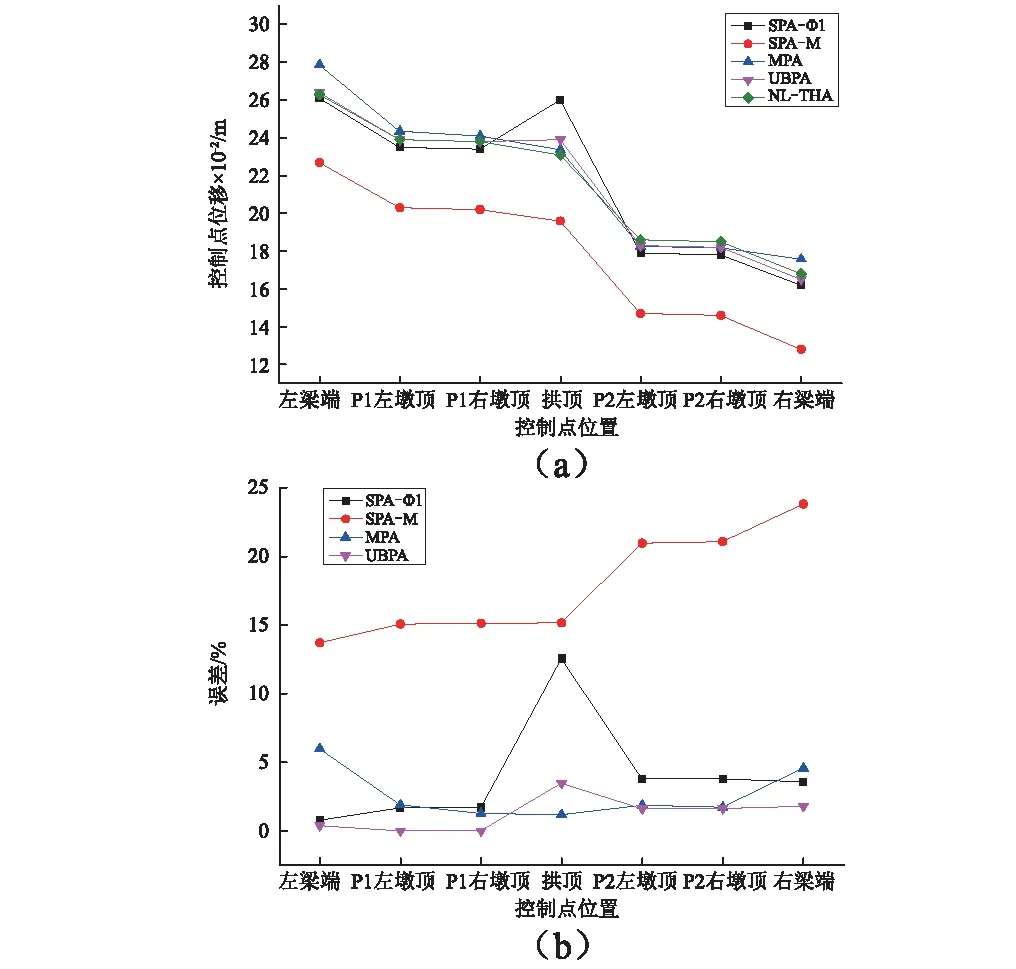
图11 桥梁结构控制点纵向位移及误差Fig.11 Longitudinal displacement and error of bridge control points

3.3 墩身纵向位移

四种Pushover方法和NL-THA方法求得左墩P1和P2墩身位移反应和误差见图12和图13。SPA-M方法比其他三种分析方法评估墩身位移误差较大，最大误差为21%，这是由于纵向地震作用使结构表现为弯曲破坏模式，而用常加速荷载主要反应结构的剪切破坏模式。UBPA方法对墩身侧移评估随着墩高减小误差逐渐增大，在墩高17 m以上，UBPA方法对墩身侧移评估精度最高，而在17 m以下，MPA方法对墩身侧移评估精度最高，可以得出高阶的模态对墩身位移具有重要影响。综合考虑UBPA和MPA方法，对墩身侧移误差评估精度可以达到9.6%。

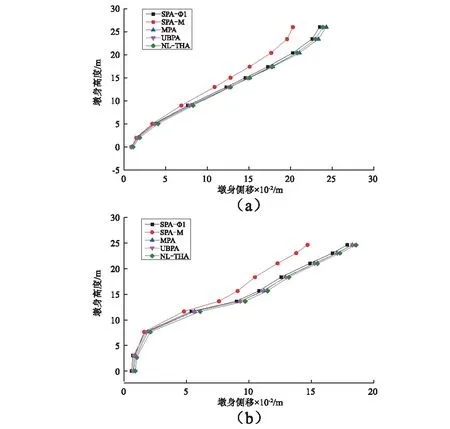
图12 P1和P2左墩纵向位移沿高度变化Fig.12 P1 and P2 left pier's longitudinal displacement along the height of changes

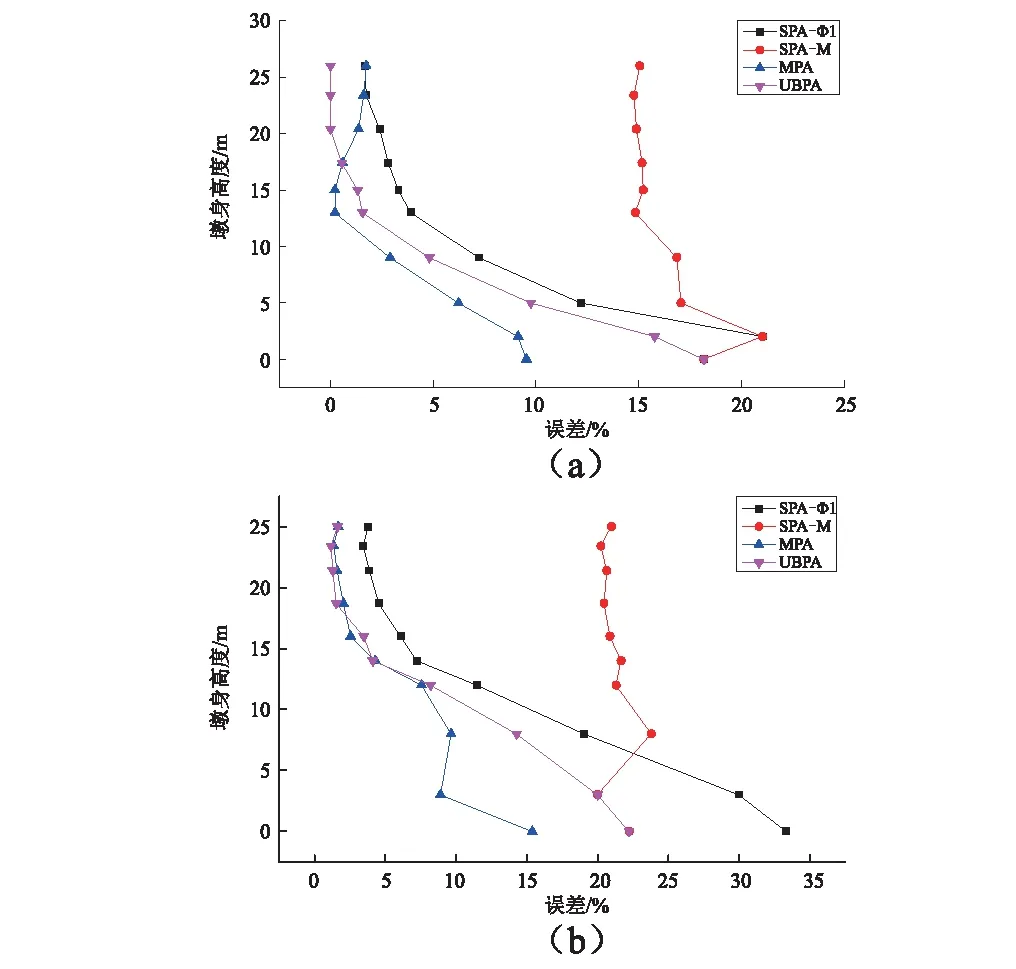
图13 P1和P2左墩纵向位移误差沿高度变化Fig.13 P1 and P2 left pier's longitudinal displacement error along the height of changes

3.4 塑性转角

图14为桥墩底截面塑性转角及误差。由图可知，SPA-M和MPA方法对墩底截面塑性转角评估精度比SPA-φ1和UBPA较差，墩底截面塑性转角的最大误差分别为26.18%、24.08%、12.04%和8.38%。显然，在P1墩底，MPA方法对塑性转角评估偏大，偏于安全，其他三种方法相对偏小，偏于不安全，尤其SPA-M最大低估误差达19.61%。在P2墩底，四种方法对塑性转角评估都相对偏小，SPA-M方法对塑性转角误差最大为26.18%，而UBPA最大误差为8.37%。在此可以看到UBPA方法对塑性转角误差评估更准确、合理。

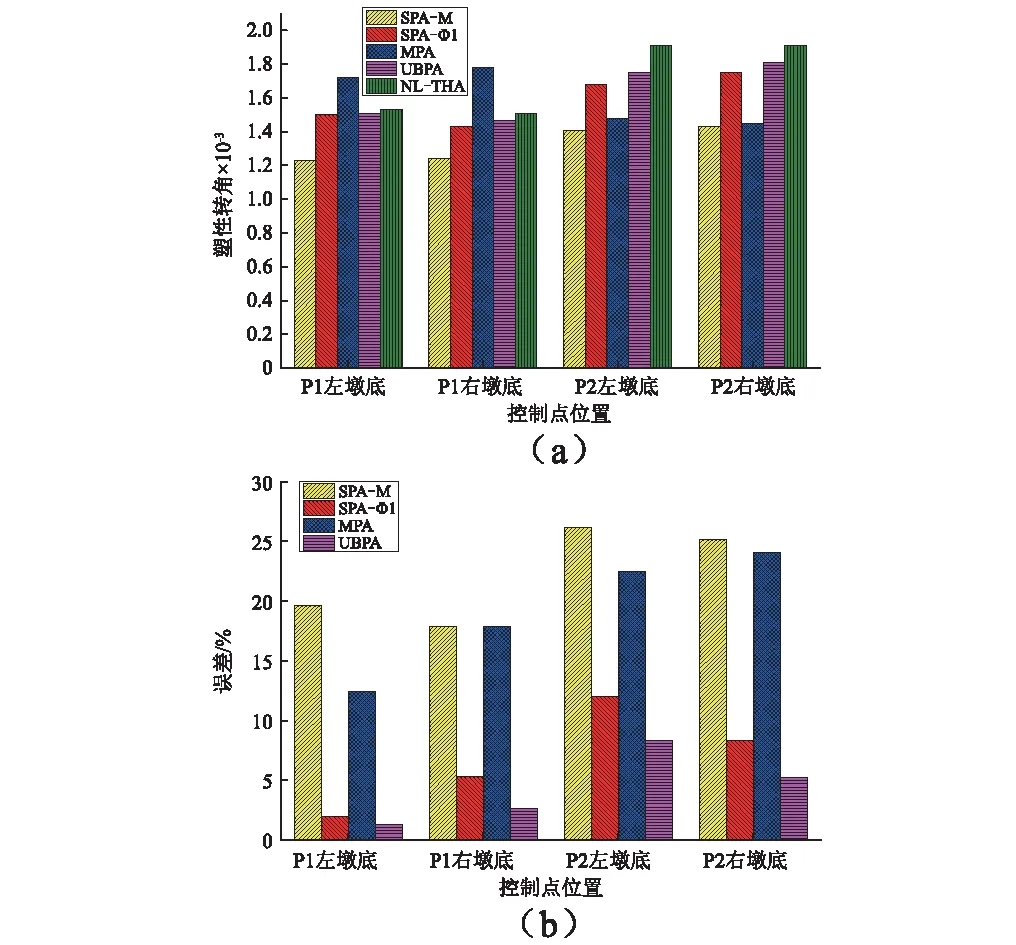
图14 墩底截面塑性转角及误差Fig.14 Plastic angle and error of pier bottom section

5 结 论

(1) 采用传统Pushover (SPA)、模态Pushover(MPA)和上界Pushover (UBPA)方法结合四种侧向力模式对桥梁进行Pushover分析，通过等效单自由度能力谱与非弹性需求谱组合求得性能点，预估目标控制点的地震需求位移。

(2) 控制点位移：SPA-M方法对桥梁控制点位移评估误差较大，而UBPA方法评估误差最小，通过拱顶位移对比，高阶模态的影响较大。

(3) 墩身纵向位移：SPA-M方法对墩身侧移评估误差较大且随墩高变化相对稳定，而UBPA对墩身上部侧移和MPA方法对墩身下部侧移评估误差比较小。

(4) 墩底截面塑性转角：SPA-M和MPA不适用于塑性区转角评估，误差超过20%，而UBPA方法准确地评价了塑性区转角。

(5) 通过SPA、MPA和UBPA方法的结果比较，综合考虑MPA和UBPA方法的优点，对CFST拱桥纵向地震需求评估与NL-THA方法分析结果趋势相似，并提高了评估精度。

[ 1 ] FREEMAN S A, NICOLETTI J P, TYRELL J V. Evaluations of existing buildings for seismic risk-A case study of Puget Sound Naval Shipyard, Bremerton, Washington [C]∥ Proceedings of U.S. National Conference on Earthquake Engineering. Berkeley: NCEE 1975: 113-122.

[ 2 ] CHOPRA A K, GOEL R K. A modal pushover analysis procedure for estimating seismic demands for buildings [J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 561-582.

[ 3 ] CHOPRA A K, GOEL R K. A modal pushover analysis procedure to estimate seismic demands for unsymmetric-plan buildings [J]. Earthquake Engineering and Structural Dynamics, 2004, 33(8): 903-927.

[ 4 ] JAN T S, LIU M W, KAO Y C. An upper-bound pushover analysis procedure for estimating the seismic demands of high-rise buildings [J]. Engineering Structures, 2004, 26(1): 117-128.

[ 5 ] POURSHA M, SAMARIN E T. The modified and extended upper-bound (UB) pushover method for the multi-mode pushover analysis of unsymmetric-plan tall buildings [J]. Soil Dynamics and Earthquake Engineering 2015, 71: 114-127

[ 6 ] PARASKEVA T S, KAPPOS A J, SEXTOS A G. Extension of modal pushover analysis to seismic assessment of bridges [J]. Earthquake Engineering&Structural Dynamics, 2006, 35(11): 1269-1293.

[ 7 ] 魏标，李建中.非规则梁桥的模态推倒分析[J].振动与冲击，2011, 30(2): 110-114.

WEI Biao，LI Jianzhong. Modal pushover analysis of an irregular continuous bridge[J]. Journal of Vibration and Shock，2011,30(2)： 110-114.

[ 8 ] 怀华锋，张少勇，盛祖光. 基于模态pushover分析的高墩桥梁地震需求研究[J].中外公路，2012，32(1): 152-159.

HUAI Huafeng，ZHANG Shaoyong，SHENG Zuguang. Research on seismic demand of high pier bridges based on modal pushover analysis [J].Journal of China & Foreign Highway，2012,32(1)：152-159.

[ 9 ] 曾森，高龙涛，陈少峰，等.钢管混凝土拱桥多振型组合pushover方法可行性例证[J]. 土木工程学报，2016，49(1): 80-85.

ZENG Sen，GAO Longtao，CHEN Shaofeng，et al. Example verification of the feasibility of multi-modal pushover method for concrete-filled steel tube arch bridges [J]. China Civil Engineering Journal，2016,49(1)：80-85.

[10] KRAWINKLER H, SENEVIRATNA G D P K. Pros and cons of a pushover analysis of seismic performance evaluation [J]. Engineering Structure, 1998, 20(4): 452-464.

[11] Building Seismic safety council. NEHRP commentary on the guidelines for the rehabilitation of buildings: FEMA-273 [R]. Washington D.C.: Federal Emergency Management Agency, 1997.

[12] 邵旭东，程翔云，李立峰. 桥梁设计与计算[M].北京：人民交通出版社，2012.

[13] 葛俊颖.桥梁工程软件Midas Civil使用指南[M]. 北京：人民交通出版社，2013.

[14] FAHJAN Y, OZDEMIR Z. Scaling of earthquake accelerograms for non-linear dynamic analysis to match the earthquake design spectra[C] ∥The 14th World Conference on Earthquake Engineering. Beijing: WCEE, 2008.

[15] European committee for standardization(CEN). Eurocode 8: design of structures for earthquake resistance. Part 2: bridges EN 1998-2:2004 [S]. Brussels: [s.n.], 2004.

[16] Applied technology council (ATC). Seismic evaluation and retrofit of concrete building: ATC-40 [R]. Califomia: Redwood City, 1996.