基于车-路相互作用的沥青路面平整度劣化研究
李 倩, 刘俊卿
(1. 西安建筑科技大学 土木工程学院,西安 710055; 2. 西安建筑科技大学 理学院,西安 710055)
路面平整度是综合反映路面使用性能的重要指标。在自然因素及行车荷载的作用下,特别是在行车动荷载的作用下,路面平整度将出现衰减。
国外关于车辆动载作用下路面平整度劣化的研究已经进行了许多有意义的工作。Cebon等[1-2]认为行驶中的车辆荷载沿轮迹分布具有空间可重复性,路面上存在某些位置总受到车辆荷载峰值作用,在这些位置上的路面必定将先破坏;Mamlouk[3]指出路面不平整使行驶中的车辆荷载增加,而该荷载的激增又使路面平整度恶化,基于此提出了车辆与路面耦合的概念;Papagiannaki等[4]用小波理论探讨了重型车辆的动荷载和路面不平度之间的关系;Obrien等[5]考虑轮迹的空间可重复性,基于力学-经验法建立了一个重型车队与路面相互作用的数值模型,用来预估车辆动载长期作用下沥青路面平整度的衰减及路面结构的损伤。而目前国内关于这方面的研究相对较少。曹源文等[6-7]通过正弦波模拟路面不平度,基于运动车辆与不平整路面的相互耦合作用,初步构建了动荷载作用下沥青路面平整度的预估方法。
本文在以往研究的基础上,从车辆荷载对路面的长期作用出发,考虑初始路面平整度的随机特性,以某新建高速公路沥青路面为研究对象,拟基于Shell法永久变形理论及车辆-路面相互作用建立一个沥青路面平整度劣化的计算模型,以期从理论上探究我国沥青路面平整度的劣化机理及其劣化规律。
1 初始平整度下的车辆随机动荷载
本文采用双自由度1/4车辆模型来模拟车辆振动,并对该模型作如下假设:①车辆匀速行驶;②轮胎与路面是点接触且始终无跳起;③刚度与阻尼分别是位移与速度的线性函数。模型如图 1所示。
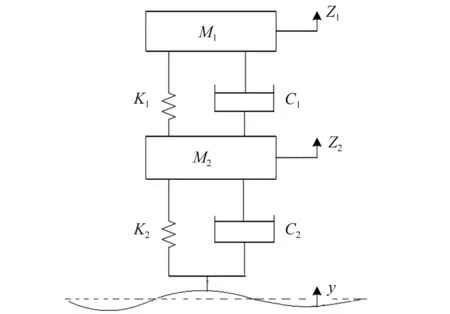
图1 1/4车辆模型Fig.1 Quarter vehicle model
如图1所示,M1、M2为悬挂部分、非悬挂部分的质量;K1、K2为悬挂系统、轮胎的刚度;C1、C2为悬挂系统、轮胎的阻尼;Z1为悬挂系统与非悬挂系统的相对位移;Z2为非悬挂系统与路面的相对位移;y为路面不平整度。
图1所示车辆模型的振动方程为
(1)
采用路面位移功率谱密度来描述路面随机不平整度特性,功率谱密度的拟合表达式[8]
(2)
式中:n为空间频率,m-1,表示每米长度中包含的波长数;n0为参考空间频率,取值为0.1 m-1;Gx(n0)为n0下的路面功率谱密度值,称为路面不平度系数,单位为(m2/m-1),其值由道路的路面等级决定;w为频率指数,对路面功率谱密度的频率结构起决定作用,取值为2;nu、nl分别为路面功率谱密度的有效空间频率上、下限。
设y0为沥青路面的初始随机不平整度序列,则
(3)
式中:m=0,1,2,…,N-1; 0≤φk≤2π;k=0,1,2,…,N/2;nk=kΔn; Δl=L/N; Δn=1/L; Δl为距离采样间隔; Δn为为采样的空间频率分辨率;L为总采集距离, m;N为采样点数。
为了使研究具有较好的准确性及可参考性,本文以新建沥青路面的平整状况作为初始条件。根据《公路工程质量检验评定标准》(JTGF 80/1—2012)[9]规定,新建沥青混凝土面层平整度质量检验标准为国际平整度指数IRI=2,因此,对应取功率谱密度Gx(n0)=6.57×10-6m3[10]。
于是,将式(3)得到的路面不平整度序列以向量的形式输入式(1)[11],采用增量形式的Newmark-β法编制Matlab程序,即可对初始不平整条件下车辆振动方程进行求解。车辆在初始不平整条件激励下对路面产生的随机动荷载可根据式(4)得到
(4)
在这种初始随机动荷载长期作用下,路面沿行车方向各点受到的荷载作用力不同,引起各点的损伤、永久变形等也不同。随着轴载作用次数增加,将引起路面平整度的劣化,这反过来又使作用在路面上的动荷载增加,形成恶性循环。因此,有必要考虑车辆与路面的相互作用来研究路面平整度的劣化过程。
2 沥青路面平整度的劣化
2.1 随机动荷载作用下沥青路面的永久变形
引起沥青路面平整度劣化的直接原因就是交通荷载长期作用下路面产生的永久变形[12],因此要研究沥青路面平整度的劣化,首先应确定随机动荷载作用下路面的永久变形。
目前我国公路以半刚性沥青路面为主,这种路面结构的车辙主要发生在沥青面层,而Shell法永久变形理论主要用来预估沥青面层的永久变形,方法简单,是国际上最有影响也是应用最广的弹性层状体系理论法[13]。考虑到动态与静态之间的差异,提出了永久变形的动态修正公式为
(5)
式中:δ为沥青面层的永久变形;CW为动态修正系数; (σav)j为第j亚层内的平均压应力;hj为第j亚层的厚度; (Smix η)j为第j亚层混合料的黏滞劲度,与温度及荷载作用时间有关,本文采用burgers模型得到混合料的黏滞劲度, 即Smix η=η1/t,η1为burgers模型中串联黏壶的黏度,t为荷载作用时间。
为了便于分析,将永久变形表示为与轴载作用次数相关的函数,设t0为一次轴载作用时间, 则式(5)可转化为
(6)
由于车辆对路面的实际作用力是受车辆作用位置、车速、路面不平整度等影响而随机变化的,因此式(6)中的压应力σav将是一个与实际路面受到的车辆动荷载大小有关的变量。由于本文以弹性层状体系理论为背景,σav与车辆荷载线性相关,可通过计算不同荷载作用下面层各亚层的压应力σav,对其进行线性拟合,得到σav与轮胎动荷载之间的函数关系
σavj=fj(Pd)
(7)
将式(7)代入式(6),就得到了随机动荷载作用下沥青路面的永久变形计算模型。
2.2 路面平整度的劣化模型
路面建成以后,要承受车辆荷载百万甚至上千万次的作用,而每一次荷载作用产生的永久变形很小,对动荷载几乎不产生影响,为了节省计算成本,本节采用增量型的永久变形预估模型,即每隔ΔN次对式(6)中的动荷载进行一次修正。
第i个增量步结束后路面纵向各点产生的永久变形增量为
(8)
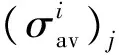
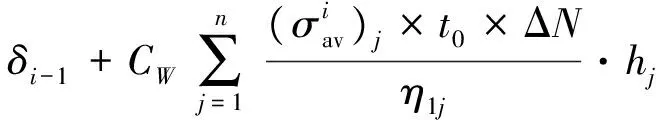
(9)
则i个增量步后,初始路面不平整度可更新为
yi(x)=yi-1(x)-Δδi(x)
(10)
每个增量步最后将得到的yi转换成具有零均值的随机不平整度以方便分析。
通过将式(7)~式(10)与前面的初始随机动荷载计算过程,即式(1)~式(4)联立,通过划分能够满足精度要求的加载增量步对路面平整度及车辆动荷载进行循环更新,即可建立考虑车-路相互作用的平整度劣化计算模型。
本文采用方根法进行计算:对所得矩阵每行分别求和、开方,再进行归一化处理,得出权值。最后计算结果为W=(0.4 155,0.2 926,0.1 070,0.1 849),最大特征根λmax=4.0 710,当判断矩阵的阶数大于2时,需要一致性检验。
为了实现这一复杂的计算过程,仍基于Matlab平台,在前述基于Newmark-β法的振动方程求解程序里嵌入考虑荷载增量步的循环,开发了一个完整的Matlab求解程序。可通过试算确定加载步数。
3 模型参数及验证
3.1 车辆模型参数
选取后轴轴载为标准轴载BZZ-100的车辆参数,简化为图1所示的1/4车辆模型,模型各参数如表1所示。

表1 车辆模型计算参数
3.2 路面模型及参数
选取某半刚性沥青试验路[14]作为算例,各结构层参数如表2所示。
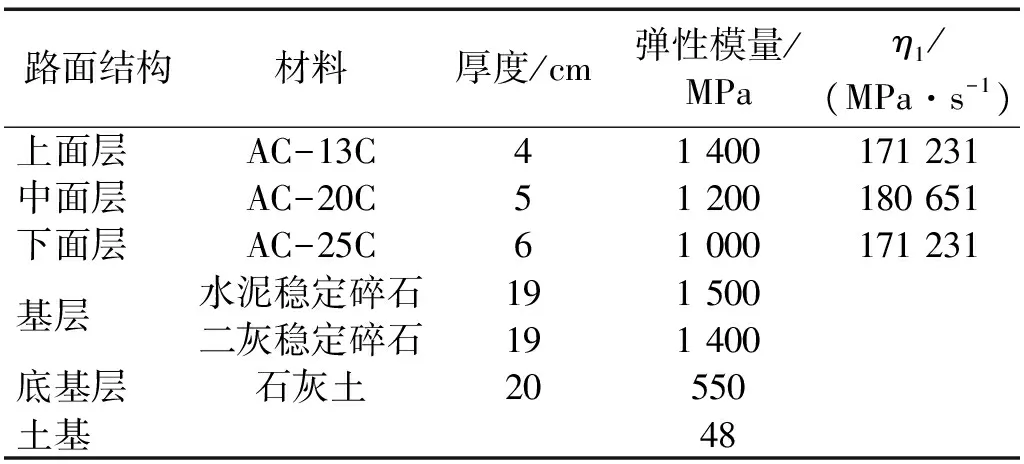
表2 沥青路面结构各结构层参数
沿道路走向取路长L=200 m为研究对象,距离采样间隔取0.1 m,采样点共2 000个,代入式(3),通过Matlab仿真得到该路面新建成时的随机不平整度序列,如图 2所示。设车辆行驶速度为v,道路纵向坐标x,则由t=x/v可将其转换到时域空间。

图2 新建沥青路面的不平整度曲线Fig.2 Roughness curves of the new pavement
通过在Matlab中调用pwelch函数,利用改进的平均周期图法,求出图2中随机不平整序列的功率谱密度模拟值,利用式(2)得到对应的功率谱密度理论值,两种结果进行比较,如图3所示。可以看出,本文仿真得到的新建路面不平度的功率谱密度模拟值均在理论值上下浮动,故仿真路面合理,可作为分析车辆动力学行为的输入激励。

图3 新建路面功率谱密度比较图Fig.3 Comparison of power spectral density of the new pavement
3.3 不同轴载作用下的σav拟合
如果保持轮胎接地长度Ld不变,根据弯沉等效可得汽车轮胎接地压强p与轴载P成正比[15],取标准轴载作用下轮胎接地压强为0.7 MPa,则标准轴载下,受动荷载的影响,轮胎的实际接地压强为p=0.7Pd/Ps。这样,按前述分析思路,基于弹性层状理论体系,计算本算例路面结构在不同荷载作用下的σav,进行线性拟合,便可将式(7)的函数关系表示为
σav1=0.79×0.7Pd/Ps+0.001
σav2=0.515×0.7Pd/Ps+0.002 3
σav3=0.355×0.7Pd/Ps+0.001 3
(11)
式中:Ps=50 kN,为1/4车辆模型静载,即标准轴载。
3.4 模型验证
取轮胎接地长度Ld=0.302 m,则一次轴载作用时间t0=0.302v。根据试验路通车一年内的交通量观测及轴载调查结果,按弯沉等效原则换算为累计标准轴次为95万次,车道横向分布系数取0.43。经过试算,以月为单位进行路面平整度更新可满足精度要求,模型及程序表现出极好的收敛性。因此,计算时取12个增量步,一个增量步内的轴载作用次数ΔN为79 167次。车辆行驶速度取路面代表速度v=80 km/h,其他参数取值如前所述。将这些参数输入到前面编制的Matlab程序中进行求解,得到该路段通车一年后的永久变形计算值,并与该试验路的实测值进行对比,如表3所示。

表3 永久变形计算值与实测值
本文的永久变形计算模型是基于Shell法永久变形理论推导得到的,因此将本文模型得到的永久变形随时间发展曲线与Shell法进行对比,如图4所示。
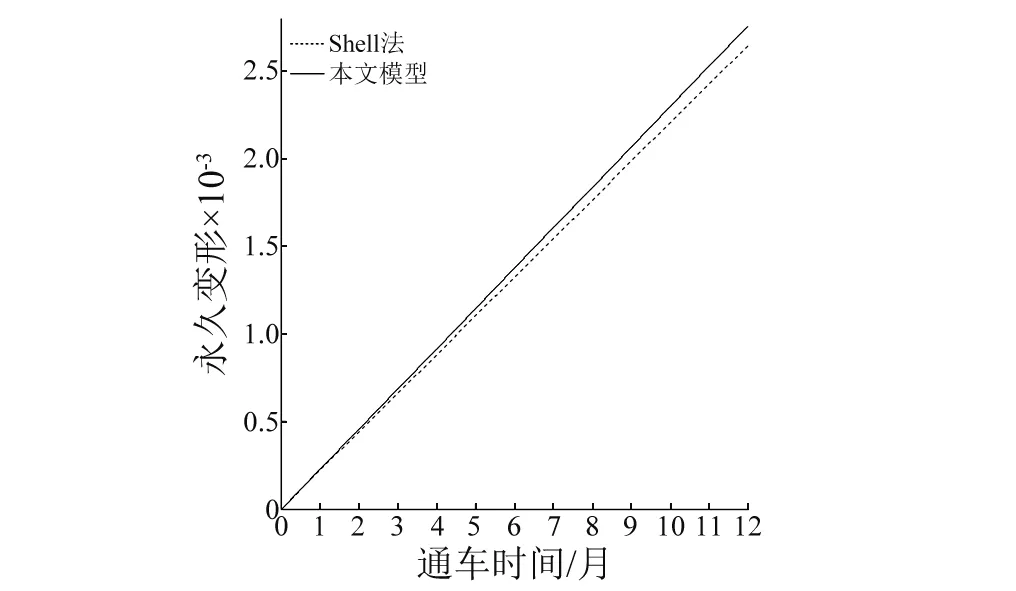
图4 永久变形与时间的关系曲线Fig.4 The relationship between permanent deformation and time
通车一个月后,两种模型得到的永久变形相等,均为0.22 mm。随着车辆作用次数增加,二者出现了分化:Shell法的永久变形随时间呈线性增大,而本文方法得到的永久变形呈非线性增大,且增大速率越来越快,与前者的差异逐渐拉大。通车一年后,本文模型计算结果为2.8 mm,比Shell法得到的2.6 mm增大了7.6%。可见,随着通车时间继续增加,路面平整度劣化将引起永久变形发展速率进一步增大,而Shell法的误差也将越来越大。因此,考虑车-路相互作用与否,也将影响沥青路面永久变形预估方法的精确性。
4 计算与分析
基于上节的分析,仍以表2的试验路为例,分析轴载长期作用过程中路面平整度的劣化以及随机动荷载的演化规律。计算过程中增量步ΔN取75 000次,轴载累计作用1 500万次,分为200个增量步。其他参数不变。
4.1 路面平整度的劣化机理
车速为60 km/h时,标准轴载累计作用375万次、750万次、1 125万次、1 500万次,路面不平整度曲线如图5。沿道路纵向取80~100 m的路段以方便分析。可以看出,沥青路面平整度的劣化沿轮迹具有空间可重复性。即,随着轴载作用次数增加,路面上一些相对凹陷的地方会更凹,如x=90~92 m处,记为计算点A,而另一些相对凸起的地方则更凸,如x=87~88 m位置,记为计算点B。
图6为对应的动荷载沿道路纵向的分布,受平整度劣化的影响,其变化也具有空间可重复性:随轴载作用次数增加,动荷载在相对凹陷的地方逐渐增大,而凸起的地方动荷载却越来越小。

图5 不同轴载次数下路面不平整度分布曲线Fig.5 Pavement roughness distribution curve under different load repetition numbers
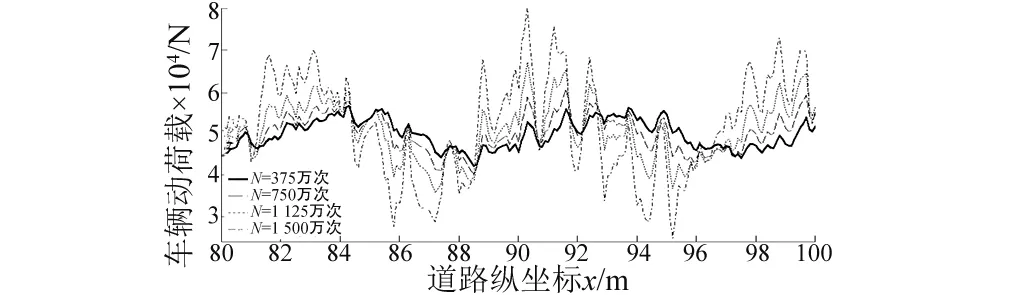
图6 不同轴载次数下动荷载分布曲线Fig.6 Dynamic load distribution curve distribution under different load repetition numbers
为了分析这一现象产生的原因,图7、图8分别给出计算点A、B的永久变形增量以及车辆动荷载随轴载作用次数的演化规律。
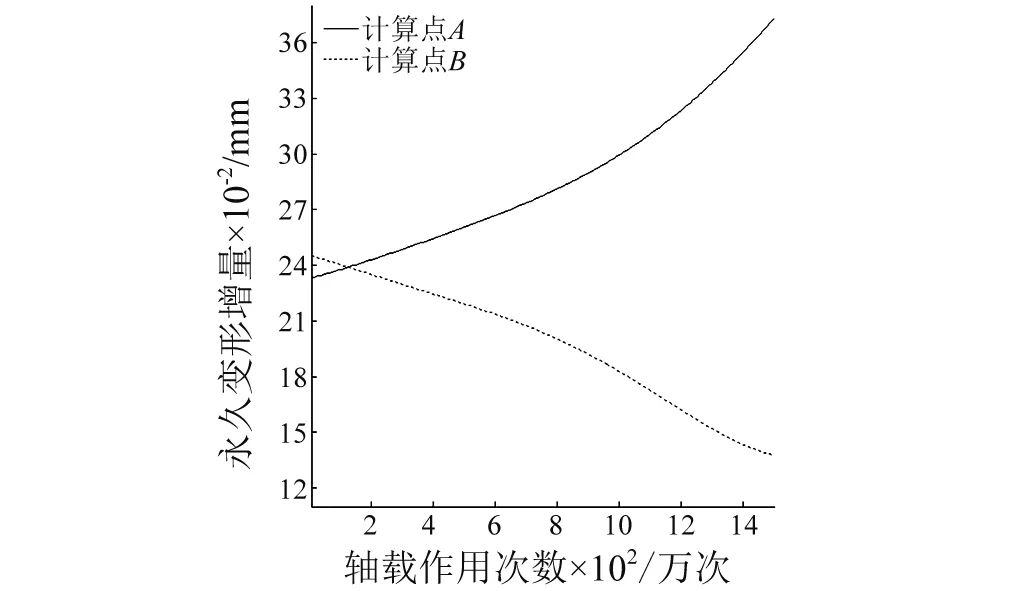
图7 计算点永久变形增量变化曲线Fig.7 Change of permanent deformation increment of the calculating points
点A永久变形增量随轴载作用次数逐渐增大,且增大速率越来越快,呈非线性趋势,点B则呈非线性减小,二者之间的差异迅速拉大,这将导致其永久变形的累积差异增大,从而引起路面平整度的劣化。而由图8所示,点A、点B受到的车辆动荷载与其永久变形增量变化趋势一致,且点A受到的动荷载总是大于车辆自重,而点B总小于车辆自重。这种凹凸点所受荷载作用不一的原因可能与向心力有关,路面上凹凸越厉害的地方,车辆越容易受向心力的影响,在凸起处,如点B,车辆对路面的作用小于车身自重,而凹陷处,如点A,则大于车身自重。这将引起路面上各点的永久变形累积速率出现差异,随着轴载次数增加,这种差异逐渐拉大,从而引起路面平整度的劣化。这反过来又使各点所受的动荷载差异增大,形成恶性循环。

图8 计算点动荷载变化曲线Fig.8 Change of dynamic load of the calculating points
4.2 路面平整度的劣化规律及影响因素分析
对于随机过程,最基本的数字特征为均值、方差和均方值,本节以平整度均方差来表征路面平整状况,其值越大,说明路面平整状况越差。
车辆分别以50 km/h、60 km/h、70 km/h、80 km/h的速度在路面上行驶时,路面平整度方差随轴载作用次数的变化曲线如图9所示。可以看出,车辆作用初期,平整度劣化较慢,车速对其影响不大。但是随着轴载作用次数增加,路面平整度劣化得速度越来越快,呈非线性趋势,且车速对其劣化速度的影响也越来越显著,基本表现为:车速越小,路面平整度劣化得越快,这种非线性越强,车速越大则劣化得较慢。这是因为车速越小,车轮经过路面上特定点所需的时间越长,路面上各点产生的永久变形差异也就越大,进而加剧了路面平整度的劣化。
可见,应从行驶安全、路面损伤等方面综合评估,确定合理的行车速度。

图9 不同车速下路面平整度变化曲线Fig.9 Change of pavement evenness under different vehicle velocity
为了分析轴载对沥青路面平整度劣化规律的影响,车辆后轴轴载分别按标准轴载的1倍、1.2倍、1.4倍来计算,车速按80 km/h计算,则不同轴载下沥青路面平整度的劣化曲线如图10所示。可以看出,轴载对路面平整度劣化速度的影响在车辆作用初期表现不明显,随着道路服役时间增加,车辆轴载的增大将引起路面平整度劣化的速度加快。如轴载作用1 500万次后,140 kN的轴载作用下路面平整度标准差增大了68%,而标准轴载下只增大了13%。
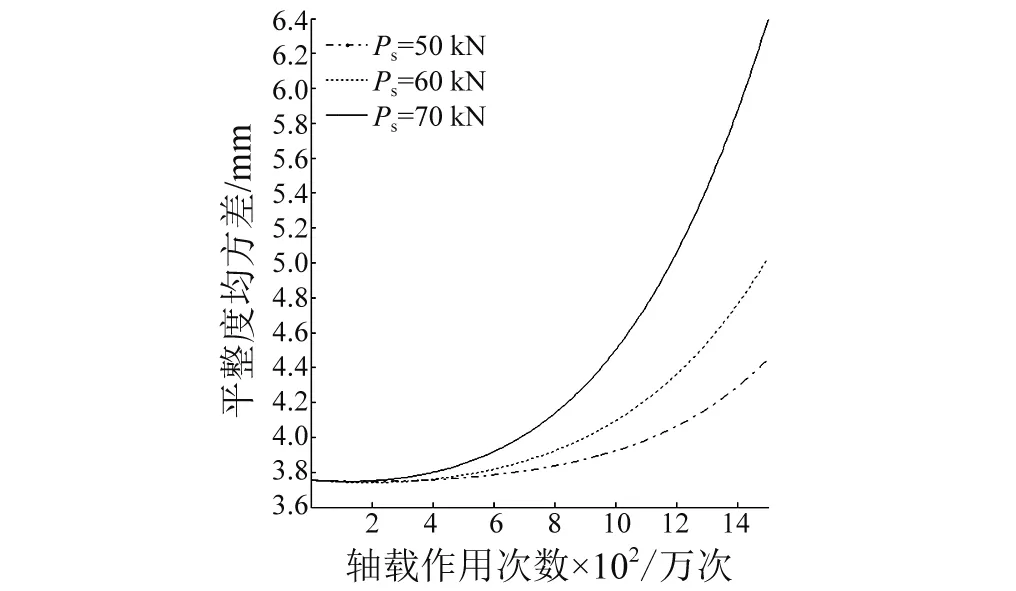
图10 不同轴载下路面平整度变化曲线Fig.10 Change of pavement evenness under different axle load
5 结 论
(1) 基于Shell法永久变形理论, 建立了一个考虑车-路相互作用的平整度劣化计算模型,采用Matlab语言开发了该模型的求解程序,通过试算,程序能满足精度要求。通过将某试验路通车一年后产生的永久变形计算值与实测值进行对比,验证了本文模型的合理性及可靠性。
(2) 基于该模型分析了轴载长期作用过程中沥青路面平整度的劣化机理:随着轴载作用次数增加,车辆动荷载的变化沿轮迹均具有空间可重复性,这将引起路面上各点的永久变形累积速率出现差异,随着轴载次数增加,这种差异逐渐拉大,从而引起路面平整度的劣化。这反过来又使各点所受的动荷载差异增大,形成恶性循环。
(3) 对路面平整度的劣化规律进行了影响因素分析。结果表明:平整度标准差随轴载作用次数的增加呈不可收敛的非线性增大,而车速越小、轴载越大,平整度劣化得越快,对路面越不利。
(4) 本文在建立沥青路面平整度劣化模型时对路面的损伤问题进行了简化,行车载荷考虑了标准轴载,而重载车辆作用下相关规律是否呈几何倍数增长值得今后进一步分析。因此后续进行这一课题的研究还需更深入的考虑。
[ 1 ] CEBON D, WINKLER C B. A study of road damage due to dynamic wheel loads using a load measuring mat [M]//Strategic Highway Research Program. Washington D. C: National Research Council, 1991.
[ 2 ] COSTANZI M, CEBON D. An investigation of the effects of lorry suspension performance on road maintenance costs[J]. Journal of Mechanical Engineering Science, 2007, 221(11): 1265-1277.
[ 3 ] MAMLOUK M S. General outlook of pavement and vehicle dynamics[J]. Journal of Transportation Engineering, 1997, 123(6): 515-517.
[ 4 ] PAPAGIANNAKI A T, ZELELEW H M, MUHUNTHAN B. A wavelet interpretation of vehicle-pavement interaction[J]. International Journal of Pavement Engineerning, 2007, 8(3): 245-252.
[ 5 ] OBRIEN E J, TAHERI A. Numerical integration approach to the problem of simulating damage in an asphalt pavement [J]. International Journal of Pavement Engineering, 2012, 13(4): 339-349.
[ 6 ] 曹源文,梁乃兴,徐建平.行车动荷载作用下路面平整度的预估[J].长安大学学报(自然科学版), 2004, 24(4): 22-25.
CAO Yuanwen, LIANG Naixing, XU Jianping. Calculation of pavement evenness under dynamic load of moving vehicle[J]. Journal of Chang’an University(Natural Science), 2004, 24(4): 22-25.
[ 7 ] 秦旻,梁乃兴,陆兆峰,等. 动荷载作用下沥青路面寿命预估[J].公路交通科技, 2010, 30(3): 34-38.
QIN Min, LIANG Naixing, LU Zhaofeng, et al. Residual life forecast method of asphalt pavement based on evenness[J]. Journal of Highway and Transportation Research and Development, 2010, 30(3): 34-38.
[ 8 ] 车辆振动输入与路面平度表示方法: GB T 7031—1986[S].北京:中国标准出版社,1987.
[ 9 ] 公路工程质量检验评定标准: JTGF 80/1—2012[S]. 北京:人民交通出版社, 2012.
[10] 程国勇,侯栋文,黄旭栋.基于飞机竖向加速度的道面不平度限值标准研究[J].振动与冲击, 2017, 36(9): 166-171.
CHENG Guoyong, HOU Dongwen, HUANG Xudong. Pavement roughness limit value standard based on aircraft vertical acceleration[J]. Journal of Vibration and Shock, 2017, 36(9): 166-171.
[11] 李倩,刘俊卿,陈诚诚. 随机激励下四自由度车辆-道路耦合系统动力分析[J].应用数学和力学, 2015, 36(5): 460-473.
LI Qian, LIU Junqing, CHEN Chengcheng. Dynamic analysis of the four-degree vehicle-road coupling system under random excitation[J]. Applied Mathematics and Mechanics, 2015, 36(5): 460-473.
[12] 汤文,孙立军. 基于遗传算法的汲青路面永久变形预估方法[J]. 武汉理工大学学报, 2008, 30(12): 42-45.
TANG Wen, SUN Lijun. Permanent deformation evaluation model of asphalt concrete pavement based on genetic algorithms[J]. Journal of Wuhan University of Technology, 2008, 30(12): 42-45.
[13] 苏凯,孙立军. 高等级沥青混凝土路面车辙预估方法研究综述[J]. 公路, 2006, 18(7): 18-24.
SU Kai, SUN Lijun. A summary of rutting prediction method on high grade asphalt concrete pavements[J]. 公路, 2006, 18(7): 18-24.
[14] 何兆益,雷婷,王国清,等. 基于动力问题的高等级公路沥青路面车辙预估方法[J].土木工程学报, 2007, 40(3): 104-109.
HE Zhaoyi , LEI Ting, WANG Guoqing, et al. Calculation method for prediction of highway asphalt pavement rutting under dynamic loading[J]. China Civil Engineering Journal, 2007, 40(3): 104-109.
[15] 李海军,黄晓明. 重载条件下沥青路面按弯沉等效的轴载换算[J].公路交通科技, 2004, 21(7): 5-8.
LI Haijun, HUANG Xiaoming. Axle load conversion formula based on deflection equivalent for semi-rigid base asphalt pavement under heavy-load[J]. Journal of Highway and Transportation Research and Development, 2004, 21(7): 5-8.

