古建筑木结构榫卯节点刚度的地震损伤分析和识别
薛建阳, 白福玉, 张锡成, 隋 , 周超锋
(西安建筑科技大学 土木工程学院,西安 710055)
中国古建筑木结构各构件之间连接主要采用由榫头和卯孔组成的榫卯节点构造。榫卯节点的刚度变化属于非线性变化。榫卯节点具有很好的抵抗水平推力作用,能够有效减少结构的地震响应[1]。强震激励,榫卯节点张合和榫头拔出明显,榫卯节点承载能力下降,榫卯连接柱架层变形增大,结构倒塌危险性较大。在漫长的历史长河中,由于历史地震作用影响,榫卯节点松动、拔榫损伤,结构整体抗震性能减弱,结构剩余寿命缩短。确立榫卯节点的损伤刚度和提前辨识刚度参数,对古建筑损伤评估和维修保护具有重要指导意义。
王晓燕等[2]采用最小二乘和扩展卡尔曼滤波方法反演系统地震载荷和识别结构动态参数。何浩祥等[3]用静动力凝聚和扩展卡尔曼滤波对连续梁进行了刚度和阻尼损伤识别。赵博宇等[4]完成了扩展卡尔曼滤波算法对在噪声较大环境下的结构质量、阻尼和刚度识别,更新了长期不确定振动台模型。王鑫等[5]对随机激励作用下的古木结构梁上各节点的加速度响应信号进行小波包分解,提出了小波包能量曲率差损伤识别指标,通过此指标进行古木结构的损伤识别。Weng等[6]提出了识别节点模态参数的子空间、有限元模型修正和非线性最小二乘结合的方法,这种方法识别过程耗时。Wu等[7]提出了加权最小二乘和贝叶斯结合的方法;Xu等[8]提出了节点损伤指数和二阶特征灵敏度近似方法。刁延松等[9]利用振动传递率函数和统计假设检验对海洋平台结构进行了损伤识别研究。郑泽栋等[10]利用结构响应功率谱密度函数对结构损伤参数的灵敏度实现结构损伤识别。罗钧等[11]根据单元损伤系数方程和约束线性最小二乘法对剪切型框架结构损伤进行了定位和定量识别。
本文根据西安建筑科技大学古建筑抗震课题组1∶3.52殿堂式古建筑木结构振动台试验模型,建立了结构简化力学模型,推导了结构状态方程和观测方程。振动台试验确定了地震作用下榫卯节点刚度损伤演化规律,利用静动力凝聚方法建立了结构刚度与榫卯节点刚度之间关系。进行了力锤敲击测试试验和仿真计算,获得了结构柱架层和乳栿层位移、速度和加速度响应。考虑噪信比5%噪声干扰,利用偏最小二乘和扩展卡尔曼滤波方法对榫卯节点转动刚度进行了损伤识别。结果表明,基于偏最小二乘、扩展卡尔曼滤波和静动力凝聚方法对榫卯节点转动刚度识别精度较高,具有较好适用性。
1 结构状态方程和观测方程
1.1 结构简化力学模型
忽略结构空间平扭耦合作用,根据西安建筑科技大学古建筑抗震课题组1∶3.52殿堂式古建筑木结构振动台试验设计模型,选取其一榀构架为研究对象,建立平面简化力学模型,如图1所示。模型立柱与额枋榫卯连接用弹簧单元模拟,梁柱及斗拱用梁单元模拟,将结构每个区域质量分别集中于榫卯连接柱架层和乳栿层处。
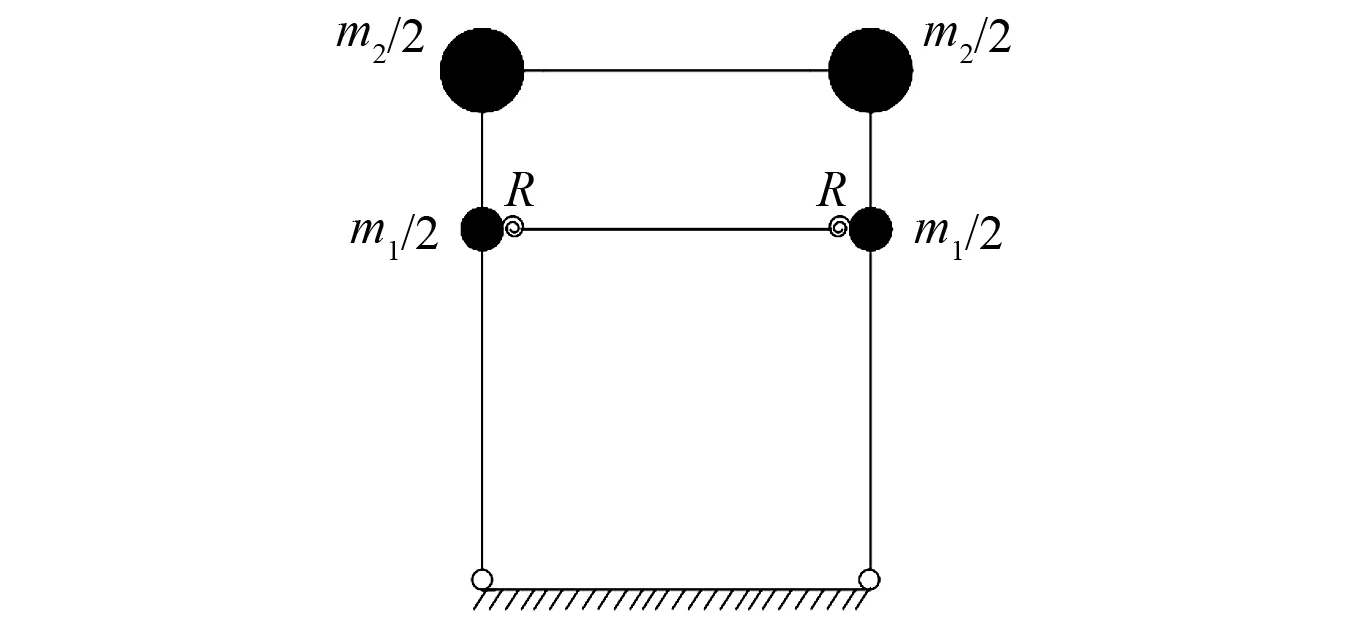
图1 平面简化力学模型Fig.1 The simplified mechanical model of timber structure
1.2 结构动力方程
(1)

设木材顺纹抗弯弹性模量为E,梁枋截面惯性矩为IB、额枋截面惯性矩为IL、立柱截面惯性矩为IC,斗拱等效抗弯刚度为EIC,榫卯节点转动刚度为R,立柱高度为h1,斗拱铺作层高度为h2,额枋和梁枋跨度为L,半刚性系数为μ。忽略梁柱轴向变形,考虑榫卯节点半刚性连接特性,根据Chopra等[12]给出的两端半刚性连接杆件、一端铰接一端固定杆件的刚度矩阵,组装确定结构整体刚度矩阵[K]各元素
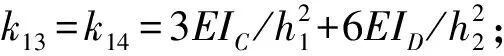

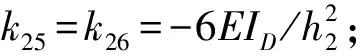
k33=k44=3EIC/h1+(4+12μ)EIL/(R*L)+4EID/h2;
k34=2EIL/(R*L);
k35=2EID/h2;k36=0,k45=0;
k46=2EID/h2;k56=2EIB/L;
k55=k66=4EIB/L+4EID/h2;μ=EIL/(RL);
R*=1+8μ+12μ2。
1.3 结构状态方程和观测方程
动力方程分块形式为
(2)

利用静动力凝聚法,消除具有零质量转动项,凝聚后结构动力方程为
(3)
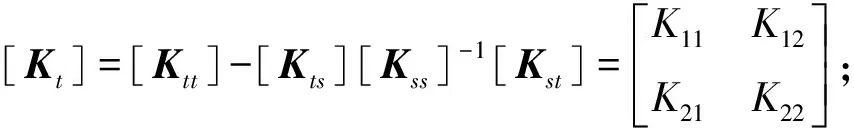
将动力方程式(3)转化为状态方程
(4)
令结构柱架层和乳栿层平动速度δ3、δ4,将结构刚度K11、K12(K21)、K22,阻尼比ζ和结构固有频率ω看成结构的5个状态向量,结构状态方程
(5)
设结构量测值分别为Z1、Z2,结构观测方程
(6)
2 刚度识别方法
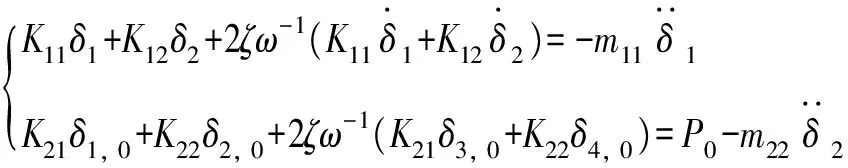
观测柱架层和乳栿层位移、速度和加速度响应;获得观测矩阵H、刚度参数X、量测Z为
X=[K11K12K22]T
(8)
首先基于奇异值分解的偏最小二乘法(PLS-SVD)计算步骤如下:
步骤1H和Z进行标准化得到H0和Z0;
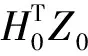
步骤3 计算H0的潜变量矩阵T和Z0的潜变量矩阵U,其中T=H0W,U=Z0C。
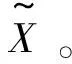
扩展卡尔曼滤波是用递推状态空间方程一阶泰勒公式进行估计的一种方法,适用剪切型结构体系参数识别。质量已知的剪切型结构体系,扩展卡尔曼滤波估计公式[13]为
(9)
式中:R为观测噪声;P为误差协方差矩阵;Φ为状态转移矩阵;G为增益矩阵。
状态转移矩阵为
(10)
式中:A为状态雅可比矩阵;H为观测雅可比矩阵;I为单位矩阵;Δt为采样时间间隔。
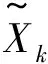
3 榫卯节点刚度损伤分析
为了研究古建筑木结构榫卯节点刚度在地震下的累积损伤,课题组制作了一个缩尺比为1∶3.52单层单开间殿堂结构当心间梁柱燕尾榫榫卯连接模型,如图2所示,模型上面嵌固配重为14 kN/m2的钢筋混凝土板作为等效屋盖荷载,4块柱础固定在2.0 m×2.2 m的振动台上。试验中分别在台面、柱脚、柱顶和乳栿处布置磁电式位移传感器、磁电式速度传感器和差容式加速度传感器。对模型分别输入50 gal、75 gal、100 gal、150 gal、200 gal、300 gal的El Centro波、Taft波、兰州波,400 gal、500 gal、600 gal、800 gal、900 gal的El Centro地震波,获得模型柱脚、柱架层、乳栿层在不同损伤工况下的位移、速度和加速度响应。

图2 古建筑木结构振动台试验Fig.2 Shaking table test of ancient timber building
试验表明,随着地震作用增加,柱架层最大侧移和榫头拔出量越来越大,直至榫头劈裂和卯口破坏,结构模型倒塌。当地震输入小于150 gal时,榫卯节点转动
不明显;地震输入200 gal时,榫卯节点转动幅度较小,未出现拔榫;当地震输入达300 gal时,柱架层最大侧移28.28 mm,榫头拔出量约为3 mm;如图3所示;当输入激励达600 gal时,柱架层最大侧移56.782 mm,榫头拔出量约为8 mm。

图3 试验现象Fig.3 The test phenomenon
根据加载过程榫卯节点转动幅度,定义工况1为震前无损工况,工况2为200 gal地震加载完时刻工况,工况3为300 gal地震加载完时刻工况,工况4为600 gal El Centro波加载完时刻损伤工况。各工况榫卯节点的滞回曲线如图4所示。

图4 不同工况下榫卯节点的滞回曲线Fig.4 The moment-rotation curve of the node under different conditions
根据滞回曲线拟合榫卯节点的骨架曲线,确定各工况下榫卯节点的割线刚度如图5所示,工况3的榫卯节点刚度损伤最大,初始刚度只有工况1的23.19%,屈服刚度只有工况1的11.31%;而工况4初始刚度较工况3增大;增大48.32%,屈服刚度较工况3减小,减小29.95%。说明随着地震作用累积增加,榫头从卯口拔出,榫头受卯口挤压加剧,榫卯节点初始刚度损伤程度先增大后减小,屈服刚度损伤程度一直增大。
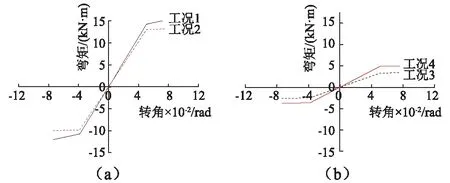
图5 不同工况榫卯节点割线刚度Fig.5 The secant stiffness of the node under different conditions
各工况榫卯节点转动刚度如表1所示。地震前榫卯节点初始刚度279.8 kN·m/rad、地震后榫卯节点初始刚度最小为64.88 kN·m/rad,发现榫卯节点初始刚度变化范围与不同松动程度下古建筑燕尾榫节点初始刚度试验[14]50~300 kN·m/rad的范围基本一致,说明了地震前后榫卯节点初始转动刚度试验结果的准确性。
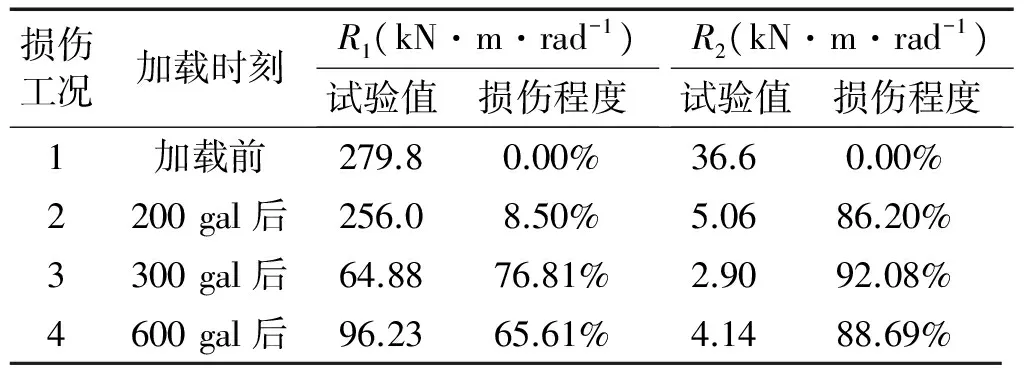
表1 不同工况下榫卯节点割线刚度值
根据静动力凝聚方法,获得了结构刚度参数K11与榫卯节点初始刚度R1近似关系,如图6所示,四种工况刚度参数K11试验值分别为107.99 kN/m、107.47 kN/m、102.87 kN/m、103.67 kN/m。
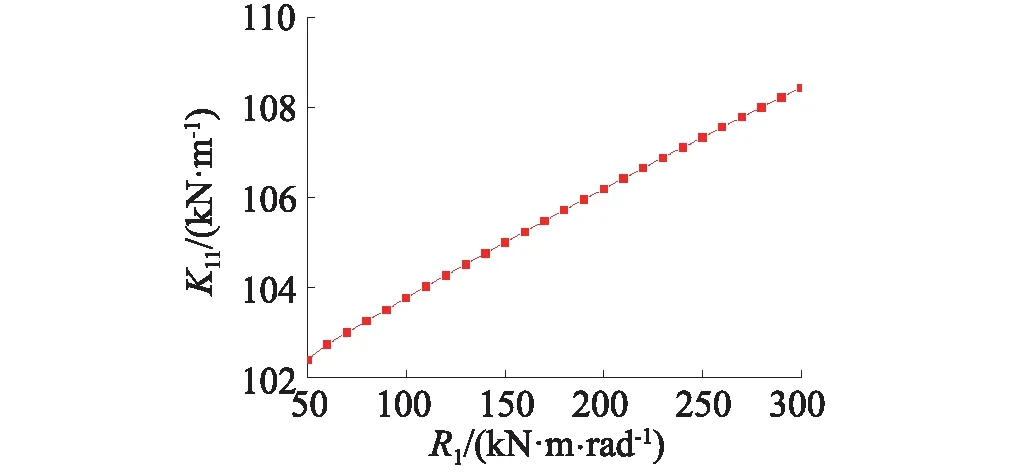
图6 结构刚度K11和节点刚度R1的关系Fig.6 Relationship between structural layer stiffness K11 and node stiffness R1
西安建筑科技大学古建筑课题组根据榫卯连接模型低周反复荷载试验,拟合榫卯节点恢复力模型,获得了榫卯节点初始刚度和屈服刚度呈一定的比例关系[15]。根据各工况榫卯节点割线刚度R1和R2,得到屈服前后割线刚度比例系数。如表2所示。

表2 R2和R1的比值
4 仿真算例
根据试验模型建立仿真模型,如图7所示。柱、额枋和梁枋用三维线性两节点单元模拟;柱与额枋榫卯连接用非线性转动弹簧单元模拟,柱脚与础石滑移连
接用轴向弹簧、阻尼器、间隙单元及滑动器构成组合单元模拟,斗拱用水平和竖向的弹簧-阻尼器单元模拟,连接弹簧单元和阻尼器假定为无质量和尺寸。屋盖质量等效到乳栿相交四个节点上,用2D单元模拟。模型材料密度为550 kg/m3,材料顺纹抗弯弹性模量为67.27 MPa,榫卯节点刚度根据表1定义,斗拱水平抗侧刚度、竖向抗压刚度由低周反复荷载试验[16]和竖向承载力试验[17]测得,柱脚与础石的滑动摩擦系数取为0.4,四种工况下有限元仿真计算采用的阻尼比例系数从振动台试验获得,分别为0.029、0.035、0.039和0.044。
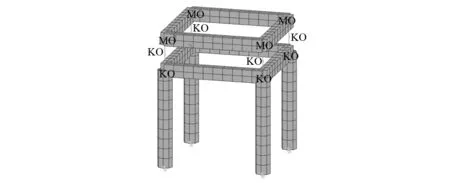
图7 木构架有限元模型Fig.7 Finite element model of wooden building
由图8可以看出,柱脚、榫卯连接柱架层和乳栿层加速度时程响应曲线基本吻合,峰值出现的时刻和大小基本相同。由于仿真模型中未完全模拟榫卯节点的滞回关系,致使响应曲线形状和走向略有不同。无损工况下仿真模型自振频率为1.88 Hz,与试验获得的一阶自振频率2.05 Hz比较,相对误差为8.29%。由此可以说明,仿真模型可满足计算精度要求。
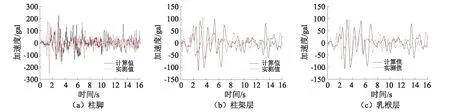
图8 加速度时程曲线Fig.8 The time history curve of the acceleration
图9选取前6阶自振频率比较,发现随节点损伤程度增加,前3阶频率变化较大,后3阶频率没有变化。仿真计算振型结果显示,第一阶振型和第二阶振型为平动,第三阶振型为结构的整体扭转,第四阶~第六阶振型表现为斗拱的竖向振动。由于累积地震作用,榫卯节点刚度损伤变小,木结构层间水平和竖向刚度损伤均变化明显,结构前3阶自振频率对应的振型变化明显。说明由于榫卯节点刚度损伤对结构低频振型敏感,计算中应选取低频部分的响应作为刚度识别主要依据。
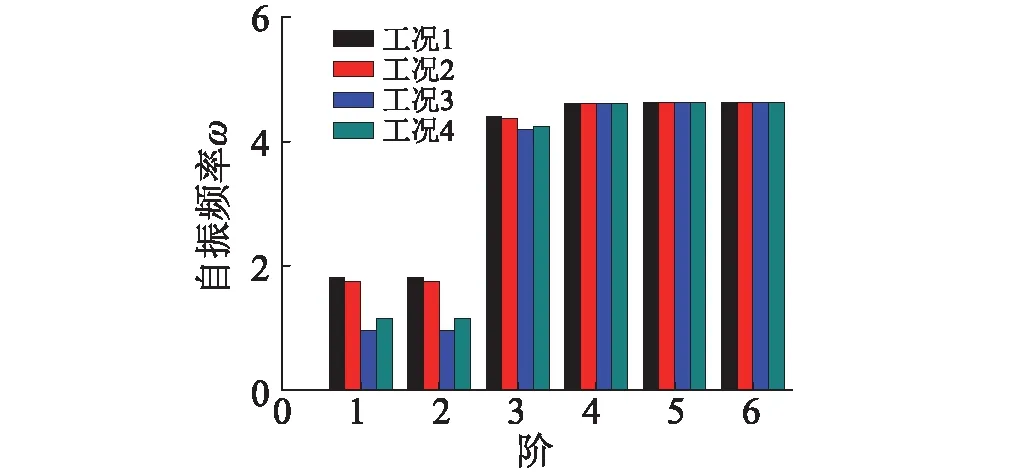
图9 不同损伤下工况结构自振频率 Fig.9 Natural frequency of different damage simulation model
仿真模拟了脉冲力锤锤击木结构上混凝土配重块,使结构产生微振动响应进行测试。忽略脉冲力锤的质量影响,脉冲激励如图10所示,由于实际施加脉冲激励时间很短,仿真计算中激励时间取为0.2 s,结构位移、速度和加速度响应采样时间设为10 s,时间步长为0.009 8 s。
图10 脉冲激励Fig.10 Pulsed excitation
比较不同损伤工况柱架层位移、速度和加速度响应发现,各工况最大负位移-0.238 mm、-0.24 mm、-0.286 mm、-0.263 mm,出现时刻为0.107 s、0.107 s、0.205 s、0.205 s;最大正位移0.204 mm、0.209 mm、0.11 6mm、0.132 mm,出现时刻为0.420 s、0.430 s、0.701 s、0.520 s。
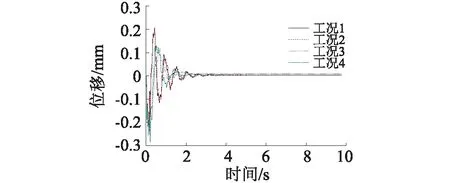
图11 各工况榫卯连接柱架层位移响应Fig.11 The time history curve of the column top under different conditions
图11说明:随榫卯节点刚度损伤加剧,柱架层负位移峰值增大,正位移峰值减小;工况3较工况1负位移峰值增大4.8%,正位移峰值减小35.3%,负位移峰值时间延后0.102 s,正位移峰值时间延后0.281 s。四种工况下结构的位移和速度响应在4 s后都基本趋于平稳。
5 榫卯节点刚度损伤识别
各工况质量矩阵中:m11=250 kg,m22=3 600 kg;各工况刚度矩阵为
刚度矩阵上标代表不同损伤工况,刚度单位为kN/m。假定阻尼比例系数已知,采样点数取100个。在无噪声干扰下,利用观测得到的榫卯连接层位移、速度、加速度响应组装观测矩阵和量测值,反演计算中观测矩阵呈病态性,对其进行奇异值分解,选取奇异值分解阶次为2,分离阶数为1,利用偏最小二乘初步估计各工况刚度参数。
无干扰下,偏最小二乘法估计各工况K11的收敛曲线如图12所示,若设error为相对误差,则各工况K11识别值与真实值相对误差均为0%。
error=(识别值-真实值)/真实值×100%
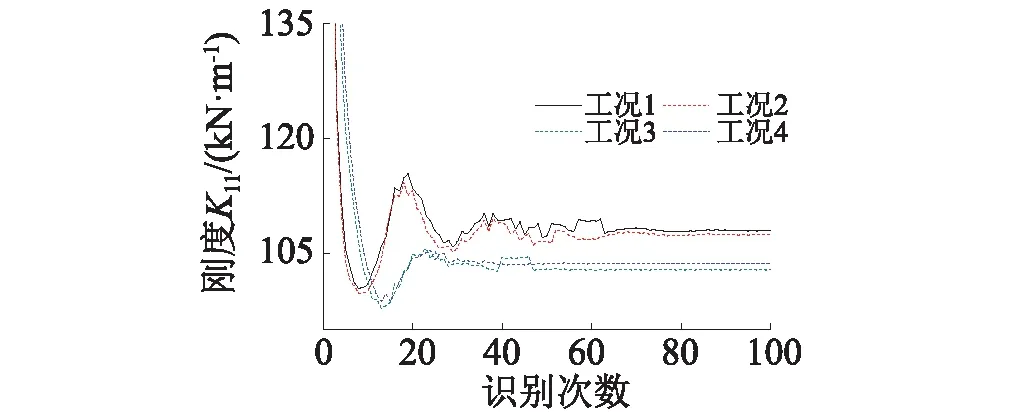
图12 噪信比为0%时各工况的K11收敛曲线Fig.12 The convergence curves of K11 under different conditions with the noise-signal ratio 0%
在力锤敲击测试模型响应中,根据输出噪声均方根与不含噪纯信号均方根之比,确定各阶段噪信的比值约为5%。因此,模拟计算中在观测位移、速度和加速度响应中加入了噪信比为5%的高斯随机噪声。设定参数收敛区域K11识别值上限为108 kN/m,下限为102 kN/m,剔除识别结果中的超限不合理数据。四种工况刚度K11整体收敛性均较好,K11识别值分别为107.91 kN/m、107.35 kN/m、102.77 kN/m和103.57 kN/m,识别值与真实值相对误差分别为-0.15%、-0.11%、-0.1%、-0.1%。
在近似估计基础上,以上述近似识别值为初值,给定初始协方差和量测值,利用扩展卡尔曼滤波方法识别各工况结构刚度K11结果如图13和表3所示。
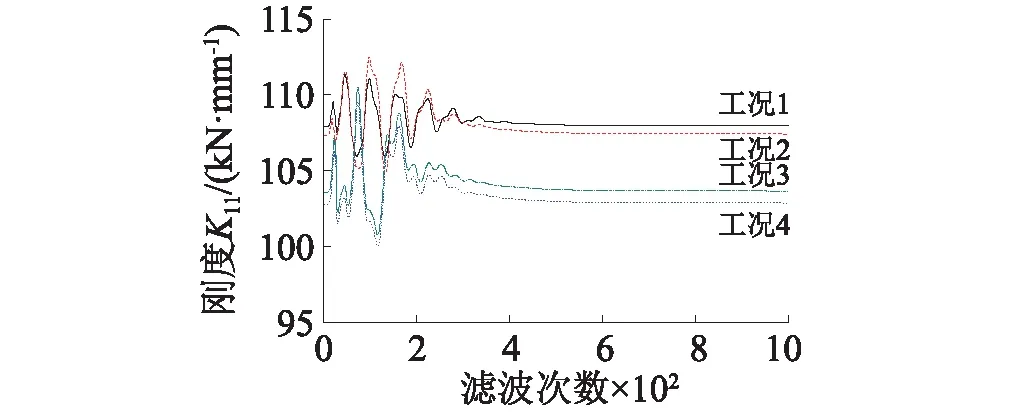
图13 噪信比5%时各工况的K11收敛曲线Fig.13 The convergence curves of K11 under different conditions with the noise-signal ratio 5%
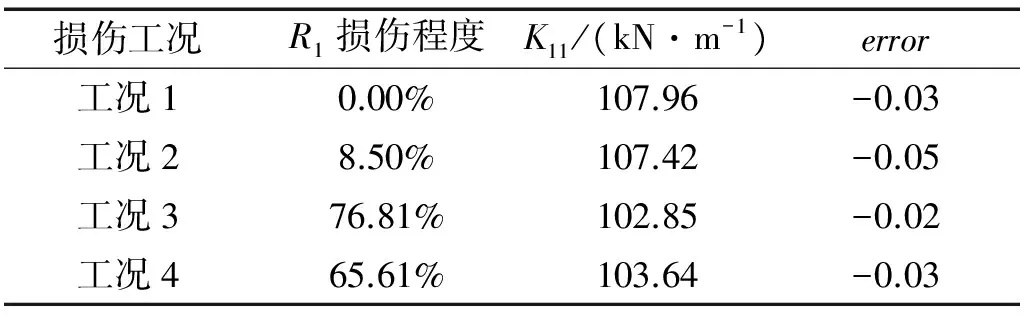
损伤工况R1损伤程度K11/(kN·m-1)error工况10.00%107.96-0.03工况28.50%107.42-0.05工况376.81%102.85-0.02工况465.61%103.64-0.03
榫卯连接柱架层水平位移识别如图14所示,三种工况下柱架层水平位移识别值和真实值时程轨迹吻合较好,说明结构刚度K11识别效果较好。
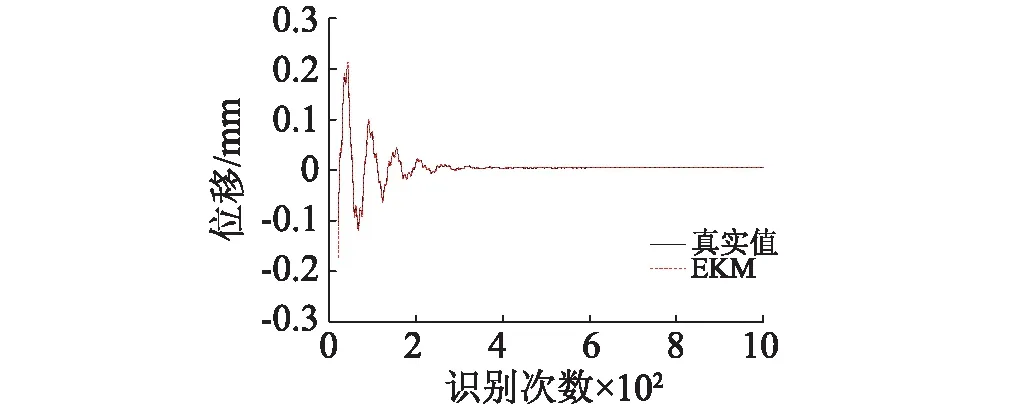
图14 工况1时柱架层位移识别值与真实值的比较Fig.14 The comparison between identification value and test value of the column top displacement under 1st loading condition
由结构刚度参数K11与R1关系线性插值计算,进一步确定榫卯节点初始刚度R1识别值,再根据榫卯节点屈服前后刚度比例系数,确定R2损伤识别值。表4结果表明,脉冲激励下静动力凝聚、偏最小二乘和扩展卡尔曼滤波的混合算法能够根据结构位移和速度响应对榫卯节点刚度进行损伤识别,识别结果精度较高,稳定性较好,具有较好的适用性;随榫卯节点地震损伤增加,初始刚度和屈服刚度识别值与试验值相对偏差增大。
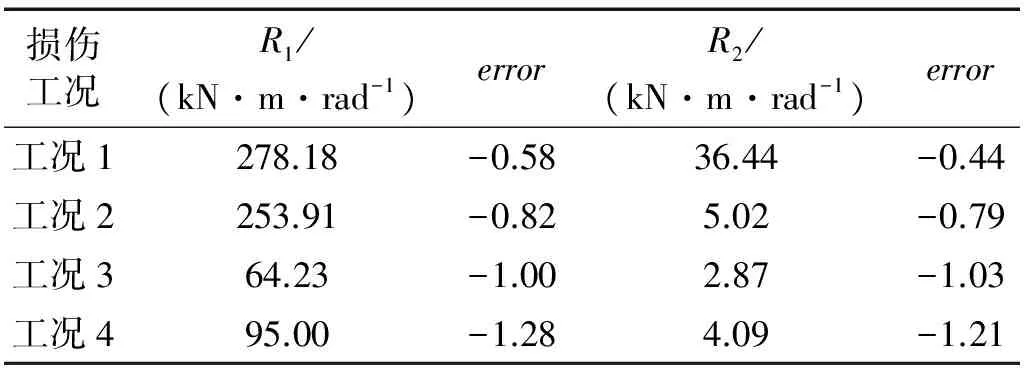
表4 榫卯节点刚度识别值
6 结 论
本文在西安建筑科技大学古建筑木结构振动台试验基础上,研究了古建筑木结构榫卯节点刚度地震累积损伤规律。基于榫卯连接木结构简化力学模型,采用静动力凝聚方法建立了结构刚度与榫卯节点刚度之间关系,推导出结构状态方程和观测方程,采用PLS-SVD和扩展卡尔曼滤波方法研究了榫卯节点地震累积损伤识别,得到以下结论:
(1) 随着结构累积损伤加剧,榫头从卯口拔出,榫头受卯口挤压加剧,榫卯节点屈服刚度损伤一直增加,榫卯节点初始刚度损伤先增大后减小。
(2) 榫卯节点损伤对低阶频率部分的振型敏感。随着榫卯节点地震损伤增加,力锤激励达峰值点所用时间越来越短;柱头、柱脚、乳栿的位移和速度最大峰值越来越大。
(3) 在噪信比5%的噪声干扰下,古建筑木结构损伤识别结果表明,静动力凝聚、偏最小二乘和扩展卡尔曼滤波的混合算法能定量识别木结构刚度损伤程度,识别精度较高。
(4) 根据静动力凝聚前后刚度矩阵可以准确建立榫卯节点屈服前刚度与结构刚度参数比例关系,结合各工况榫卯节点屈服前后刚度比,可以确定榫卯节点屈服前后割线刚度损伤识别值。
(5) 仅在结构某一位置施加脉冲激励实际操作更简单,识别结果稳定性和适用性较好。力锤敲击的人工激励获取微振动响应方法可以在识别榫卯节点刚度参数中应用。
[ 1 ] 薛建阳, 赵鸿铁, 张鹏程. 中国古建筑木结构模型的振动台试验研究[J]. 土木工程学报, 2004, 37(6): 6-11.
XUE Jianyang, ZHAO Hongtie, ZHANG Pengcheng. Study on the seismic behaviors of chinese ancient woodn buolding by shaking table test [J]. China Civil Engineering Journal, 2004, 37(6): 6-11.
[ 2 ] 王晓燕,黄维平,李华军. 地震动反演及结构参数识别的EKF算法[J]. 工程力学, 2005, 22(4): 20-23.
WANG Xiaoyan, HUANG Weiping, LI Huajun. Inversion of ground motion and identification of structural parametersby EKF [J]. Engineering Mechanics, 2005, 22(4): 20-23.
[ 3 ] 何浩祥, 吕永伟, 韩恩圳. 基于静动力凝聚及扩展卡尔曼滤波连续梁桥损伤识别[J]. 工程力学, 2015, 32(7): 156-163.
HE Haoxiang, LÜ Yongwei, HAN Enzhen. Damage detection for continuous girder bridge based on static-dynamic condensation and EKF [J]. Engineering Mechanics, 2015, 32(7): 156-163.
[ 4 ] 赵博宇,丁勇, 吴斌. 基于扩展卡尔曼估计算法的地震模拟振动台模型识别[J]. 振动与冲击, 2014, 33(12): 145-
150.
ZHAO Boyu, DING Yong, WU Bin. Identification of shaking table model for seismic simulation based on an extended Kalman estimator [J]. Journal of Vibration and Shock, 2014, 33(12): 145-150.
[ 5 ] 王鑫, 胡卫兵, 孟昭博. 基于小波包能量曲率差的古木结构损伤识别[J]. 振动与冲击, 2014, 33(7): 153-159.
WANG Xin, HU Weibing, MENG Zhaobo. Damage detection of an ancient wood structure based on wavelet packet energy curvature difference [J]. Journal of Vibration and Shock, 2014, 33(7): 153-159.
[ 6 ] WENG J H, LOH C H,YANG J N. Experimental study of damage detection by data-driven subspace identification and finite-element model updating [J]. Journal of Structural Engineering, 2009, 15(12): 1533-1544.
[ 7 ] WU J R, LI Q S. Structural parameter identification and damage detection for a steel structure using a two-stage finite element model updating method [J]. Journal of Constructional Steel Research, 2006, 62: 231-239.
[ 8 ] XU Longhe, LI Zhongxian, QIAN Jianru. Test analysis of detection of damage to a complicated spatial model structure [J]. Acta Mechanica Sinica, 2011, 27(3): 399-405.
[ 9 ] 刁延松, 徐东锋, 徐菁,等. 基于振动传递率函数与统计假设检验的海洋平台结构损伤识别研究[J]. 振动与冲击, 2016,35(2): 218-222.
DIAO Yansong, XU Dongfeng, XU Jing, et al. Structural damage identification of offshore platform based on the vibration transmissibility function and statistical hypothesis testing [J] . Journal of Vibration and Shock, 2016, 35(2): 218-222.
[10] 郑泽栋, 陈伟欢, 吕中荣, 等. 基于功率谱灵敏度分析的结构损伤识别方法[J]. 振动与冲击, 2014,33(12): 76-79.
ZHENG Zedong, CHEN Weihuan, LÜ Zhongrong, et al. Structural damage identification based on sensitivity analysis of power spectral density [J] . Journal of Vibration and Shock, 2014, 33(12): 76-79.
[11] 罗钧, 刘纲,黄宗明. 基于约束最小二乘法的剪切型框架结构损伤识别新方法[J]. 振动与冲击, 2016, 35(20): 119-124.
LUO Jun, LIU Gang, HUANG Zongming. Damage detection for a shear frame structure based on the constrained least squares method [J] . Journal of Vibration and Shock, 2016, 35(20): 119-124.
[12] CHOPRA A K, NAEIM F. Dynamics of structures: theory and applications to earthquake engineering[M]. 3rd ed. New Jersey: Pearson Prentice Hall, 2007.
[13] 李国强, 李杰. 工程结构动力检测理论与应用[M] . 北京: 科学出版社, 2002.
[14] 薛建阳,李义柱,夏海伦,等. 不同松动程度的古建筑燕尾榫节点抗震性能试验研究[J]. 建筑结构学报, 2016, 37(4): 73-79.
XUE Jianyang, LI Yizhu, XIA Hailun, et al. Experimental study on seismic performance of dovetail joints with different loose degrees in ancient buildings [J]. Journal of Buiding Structures, 2016, 37(4): 73-79.
[15] 姚侃, 赵鸿铁, 葛鸿鹏. 古建木结构榫卯连接特性的试验研究[J]. 工程力学, 2006, 23 (10) : 168-173.
YAO Kan, ZHAO Hongtie, GE Hongpeng. Experimental studies on the characteristic of mortise-tenon joint in historic timber buildings [J]. Engineering Mchanics, 2006, 23(10): 168-173.
SUI Yan, ZHAO Hongtie, XUE Jianyang, et al. Experimental study on lateral stiffness of dougong layer in chinese historic buildings [J]. Engineering Mchanics, 2010, 27(3): 74-78 .
[17] 高大峰,赵鸿铁,薛建阳. 中国木结构古建筑的结构及其抗震性能研究[M]. 北京: 科学出版社, 2008.

