找出魔术颜料
小五
1个玻璃杯:毫无悬念
一天,魔术师正准备登台表演,在做最后的物品清点。忽然,他不小心将1瓶魔术颜料放进了装有14瓶普通颜料的箱子里。这些颜料都是黄色的,把它们滴进水里,水会变成淡黄色。不过,魔术颜料有其独特之处:水起初是淡黄色,但2分钟后,水会变成神秘的黑色。
魔术颜料可是魔术师表演时的秘密武器之一,但现在与普通颜料混淆了。魔术师只能通过测试的方法,把那瓶魔术颜料找出来。然而,登台时间就要到了,时间紧迫,他找来了4个玻璃杯,希望仅花2分钟时间就可以找出那瓶魔术颜料。
魔术师这个希望可以实现吗?4个装了清水的玻璃杯,仅2分钟时间,能检测15瓶颜料吗?
回答问题前,我们不妨先来看只有1个玻璃杯时的情况。
如果魔术师只有1个玻璃杯,毫无疑问,肯定是不能找出魔术颜料的。2分钟,1个玻璃杯只能检测1瓶颜料。我们可以根据玻璃杯内的液体是否变色,来判断那瓶颜料是普通颜料还是魔术颜料。
2分钟后,依然是淡黄色,说明是普通颜料;
2分钟后,变成黑色,说明是魔术颜料。
非常简单、清楚。接下来,我们试着将玻璃杯的数目增加到2。
2个玻璃杯:开始复杂
1个玻璃杯可以检测1瓶颜料,那么2個呢?如果答案是2瓶,那也太没有挑战性了吧!事实上,2个玻璃杯可以检测3瓶颜料。这个问题需要你稍稍转一下脑筋。
首先,我们给2个装有清水的玻璃杯编号,分别命名为A玻璃杯和B玻璃杯。
随后,我们先给A玻璃杯滴一滴1号瓶颜料,然后给B玻璃杯滴一滴2号瓶颜料。之后,我们拿起3号瓶颜料,分别往A、B玻璃杯里各滴上一滴,也就是这样(“+”代表加入):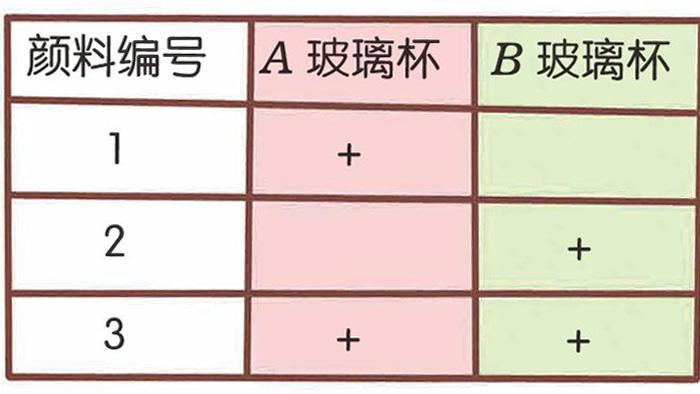
假如1号是魔术颜料,那么2分钟后,加入了1号颜料的液体会变黑,也就是说A玻璃杯的液体会变黑;假如2号是魔术颜料,那么2分钟后,变黑的是B玻璃杯的液体。如果3号才是魔术颜料,那么2个玻璃杯的液体都会变黑。
结论:2个玻璃杯可以检测3瓶颜料!
3个玻璃杯:突破极限
现在我们拿到了3个玻璃杯,先按刚刚的方法往3个杯子里滴加颜料: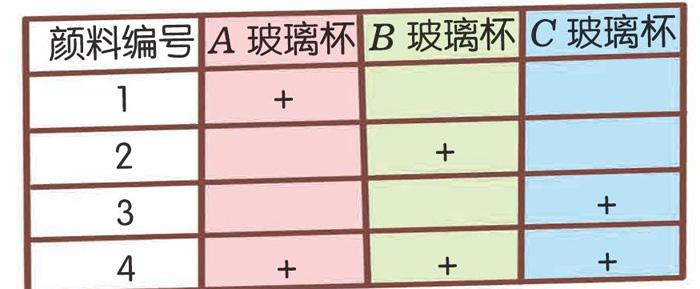
这个方法是可行的,我们可以罗列出4种可能的结果: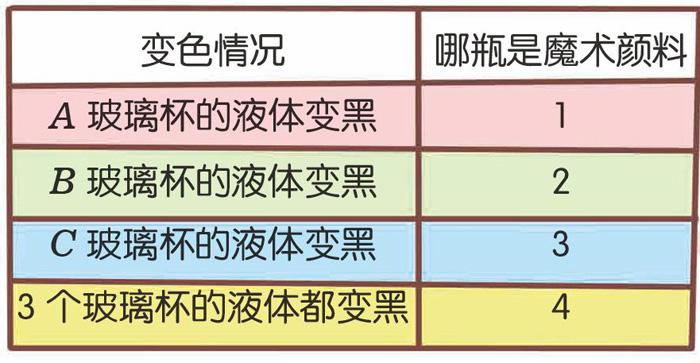
但是,你再仔细研究一下,会不会感觉有些不妥,或者不甘心?3个玻璃杯的变色情况,真的只有4种吗?
我们列举了一个玻璃杯的液体变黑和所有玻璃杯液体变黑的情况,那么有没有其中某两个玻璃杯液体变黑的情况呢?
答案是有的。也许有的同学已经想到了:
对于这3个玻璃杯,我们可以像2个玻璃杯时那样,给它们两两滴加同样的颜料。可以这样安排: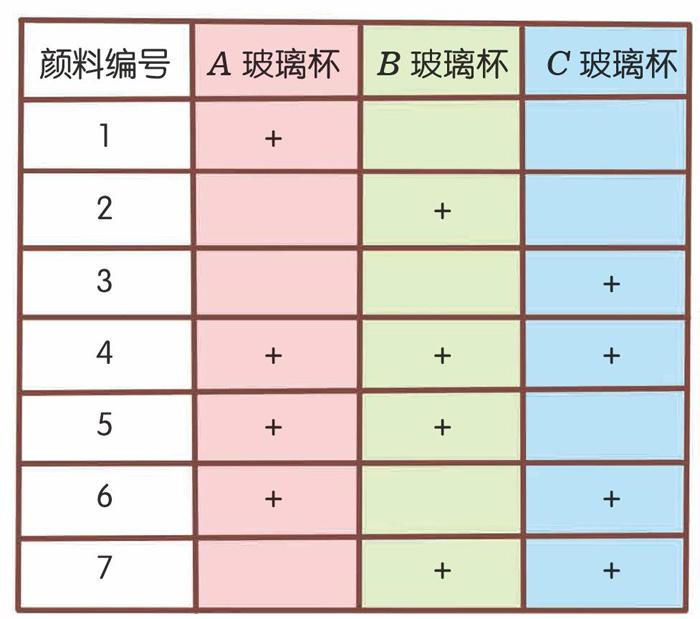
你没有看错,每个玻璃杯里要滴加4种颜料!其中1~4号瓶颜料的分配和前面的方案是一样的,只有5、6、7号瓶是新增加的。根据变色情况,我们将得到7种可能的结果: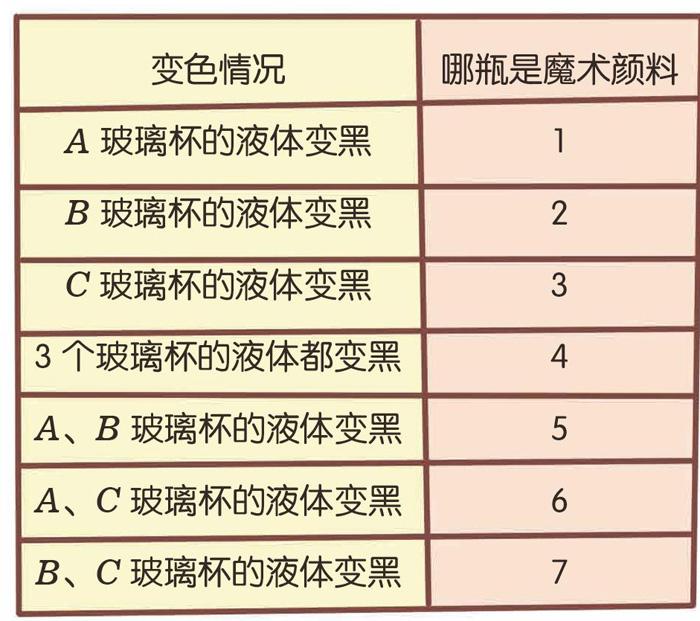
结论:3个玻璃杯可以检测7瓶颜料!
完美的超级实验
其实总结起来大家会发现,我们采用了如下策略进行检测:
给每个玻璃杯里滴加单独的1瓶颜料;
给玻璃杯中的每2个滴加1瓶新的颜料;
给玻璃杯中的每3个滴加1瓶新的颜料;
……
给所有玻璃杯都滴加同1瓶新的颜料。
为什么要这样检测?想必你很想知道其中的原理。
我们把前面得出的结论再次贴出:
1个玻璃杯检测1瓶颜料;
2个玻璃杯检测3瓶颜料;
3个玻璃杯检测7瓶颜料。
罗列完毕!观察数字,并结合我们的检测策略,我们可以推测得到这样的结论:n个玻璃杯可以检测(2n-1)瓶颜料。现在,大家可以用前面的方法进行检测,看看4个玻璃杯能给我们带来怎样的惊喜。
现在我们回到最初的问题,魔术师可以完成看似不可能完成的任务吗?当然可以!只要他手脚麻利、思维清晰,他就可以在2分钟内找出那瓶调皮的魔术颜料,顺利登台演出。
结论:4个玻璃杯能检测15瓶颜料!

