属性分类的多层次形式概念模型及动态算法研究
徐 怡,霍思林
1(安徽大学 计算智能与信号处理教育部重点实验室,合肥 230039) 2(安徽大学 计算机科学与技术学院,合肥 230601)
1 引 言
形式概念分析(Formal Concept Analysis,FCA)是Wille在1982年[1]提出的一种基于形式背景进行数据分析和规则提取的工具,强调以人的认知为中心,提供了一种与传统的、统计的数据分析和知识表示完全不同的方法,成为人工智能学科的重要研究方向,在机器学习、信息检索、和软件工程等诸多领域得到广泛的应用[2-4].
从粒计算[5]的角度,现有的形式概念分析所研究的属性大多是基于单粒度和单层次的结构[6,7],忽视了在实际应用中,属性具有多粒度和多层次的结构[8,9].例如属性“教育背景”可以细化为属性“学历”、“学位”、“毕业院校”,反之属性“学历”、“学位”、“毕业院校”也可以泛化为属性“教育背景”.不同粒度层次的属性选择会影响形式概念分析的精度或效率,所以基于形式背景构造形式概念时,根据实际问题的求解需要,将粗粒度(高层次)属性细化为两个或多个细粒度(低层次)属性,可以提高问题分析的精度,将两个或多个细粒度属性泛化为粗粒度属性,可以提高问题分析的效率.为此,本文基于属性分类的多层次结构,给出属性泛化与细化的形式概念分析方法.主要工作是:首先提出了基于形式概念分析的属性泛化与细化方法,其中属性泛化增强了属性的外在特征,提高了形式概念计算效率;属性细化增强了属性的内在特征,提高了形式概念分析精度.然后,基于属性分类层次的变化,提出了动态的形式概念构造算法,该算法通过自学习的方式对原有的知识加以使用,它不仅继承了渐进式算法的优点,还可以处理形式概念自身数据的变化.最后,通过实例和仿真实验表明本文所提算法的有效性,可以根据问题分析的需要,灵活选择属性粒度层次,即动态构造形式概念算法,可以有效提高形式概念构造的效率
第2节给出形式概念的基本定义和性质.第3节给出属性分类的泛化与细化方法,并提出了形式概念的动态构造算法.第4节,通过仿真实验验证本文所提算法的有效性.第5节总结全文.
2 形式概念分析的相关定义与算法
2.1 形式概念分析的相关定义
定义1[10].形式背景K是一个三元组:K=(G,M,I)
其中,G为所有对象的集合,M为所有属性的集合,I⊆G×M为G和M中元素之间的关系合.对于g∈G,m∈M,(g,m)∈I或者gIm表示“对象g具有属性m”.
表1 问题背景
Table 1 Problem background

学生成绩特长语言表达S1优秀唱歌不合格S2不优秀体育合格S3优秀体育不合格S4不优秀唱歌合格S5不优秀无合格
这里,表1是一个问题背景,表示5个学生的个人信息,分别代表学生的成绩、特长和语言表达.现将问题背景转化为一个形式背景K=(G,M,I)如表2所示,用1表示(g,m)∈I,用0表示(g,m)∉I.对象集G={s1,s2,s3,s4,s5}为学生集合,属性集M={a,b,c}表示学生个人信息的属性集合,a表示学习成绩是否“优秀”(用1表示优秀,0表示不优秀),属性b表示学生是否有“特长”(1表示有,0表示无),属性c表示学生“语言表达”是否合格(1表示合格,0表示不合格).对于对象g∈G和属性m∈M,(g,m)∈I表示学生具有属性m.
表2 形式背景
Table 2 Formal context
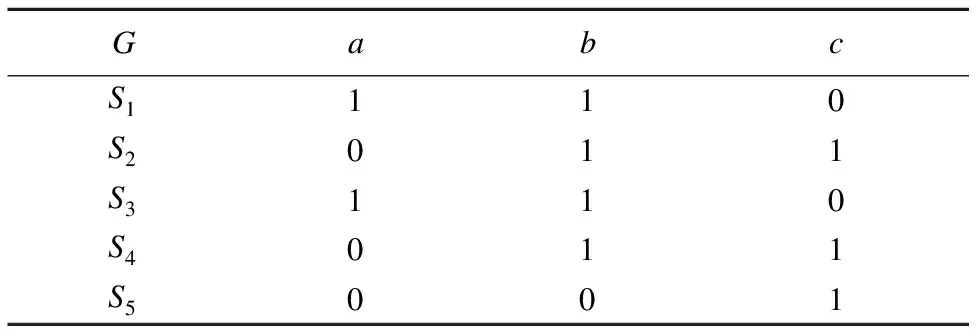
GabcS1110S2011S3110S4011S5001
定义2[10].设形式背景K=(G,M,I),对于集合A⊆G,记
AI={m∈M|(g,m)∈I,∀g∈A}
(1)
相应地,对于集合B⊆M,记
BI={g∈G|(g,m)∈I,∀m∈B}
(2)
定义3[10].设形式背景K=(G,M,I),A⊆G,B⊆M,称X=(A,B)为K的一个形式概念,如果AI=B且BI=A,此时,称A为X的外延,B为X的内涵,用B(K)表示K的所有概念组成的集合.
定义4[10].设形式背景K=(G,M,I),X1=(A1,B1),X2=(A2,B2)是K的两个概念,规定:
X1°X⟹A1⊆A2(⟹B1⊇B2)
(3)
显然,关系“°”是集合B(K)上的一个偏序,它可诱导出B(K)上的一个格结构,可以证明,它是一个完备格,并且此完备格称为形式背景K的概念格[11],在没有歧义的情况下,仍然记为B(K).
2.2 形式概念的计算方法
形式概念的计算是形式概念分析的理论基础,目前关于形式概念的计算方法主要有两种形式:批处理算法[12]和渐进式算法[13-16].其中渐进式方法效率较高,已被广泛使用.
下面通过定义6和定义7来描述渐进式算法计主要思想.
定义6.给定形式概念集B(K),对于B(K)中的任意概念(A,B),待插入的属性为m,若满足A∩mI=A,则称(A,B)是一个需要更新的概念,且更新后的概念是(A,B∪m).
定义7.给定一个形式概念集B(K),对于B(K)中的任意概念(A,B),待插入的属性为m,若满足A∩mI≠A且A∩mI⊆A,则称(A,B)将产生一个子概念,若存在B(K)中除(A,B)外其它概念(A′,B′)使A′==A∩mI,则生成的子概念是(A∩mI,B∪m),若不存在B(K)中除(A,B)外其它的概念(A′,B′)使得A′ ≠A∩mI,则生成的子概念是(A′,B′∪m).
例1.基于表2中的形式背景K,由文献[6]可计算出形式概念集合:
B(K)={({s1,s3},{a,b}),({s1,s2,s3,s4},{b}),({s2,s4},{b,c}),({s2,s4,s5},{c}),({},{a,b,c}),({s1,s2,s3,s4,s5},{})}.
3 属性分类的多层次形式概念分析
从粒计算的角度,现有的形式概念分析所研究的属性大多是基于单粒度和单层次的,忽视了在实际应用中,属性具有多粒度和多层次的结构.根据实际问题的求解需要,将粗粒度属性细化为两个或多个细粒度属性,可以提高问题分析的精度,将两个或多个细粒度属性泛化为粗粒度属性,可以提高问题分析的效率.为此,本节基于属性粒度的细化与泛化,给出基于属性分类的多层次形式概念分析.
3.1 属性分类泛化与细化形式概念计算
在实际应用中,很多属性具有多粒度的性质.例如属性“教育背景”可以细化为属性“学历”、“学位”、“毕业院校”,反之属性“学历”、“学位”、“毕业院校”也可以泛化为属性“教育背景”.不同粒度层次的选择会影响形式概念分析的精度或效率.
如何确定哪些属性需要细化或泛化,可由相关领域专家提供,也可根据训练集自动构建而成.下面给出形式概念分析中,基于属性分类的细化与泛化相关定义和性质.
首先定义两个算子“∧”和“∨”,分别称为属性细化算子和属性泛化算子.
定义8.给定一个K=(G,M,I),G={g1,g2,…,gn}是非空有限对象集,M={m1,m2,…,mr}是非空有限属性集,若属性mi∈M,可以细化为属性集P={mi1,mi2,…,mip},p≥2,则∧mi={mi1,mi2,…,mip},记细化之后的形式背景为∧K=(G,∧M,∧I).∧M=(M-{mi})∪P.∧I和I之间通常具有下述两种约束关系:
1)∀g∈G,若(g,mi)∈I,则∃mis∈P,满足(g,mis)∈∧I.
2)∀g∈G,若(g,mi)∈I,则∀mis∈P,满足(g,mis)∈∧I.
在实际应用中,∧I和I之间的约束关系,可根据实际应用的需要灵活选择,本文采用约束关系(1).
定义9.形式背景K=(G,M,I),经属性mi(mi∈M)细化得到形式背景∧K,∧mi={mi1,mi2,…,mip},p≥2,则∀(A,B)∈B(K),若mi∉B,则(A,B)∈B(∧K);若mi∈B,则(A,B)在B(∧K)中表示为概念
下面给出一些性质说明K和∧K的关系.
性质1.给定形式背景K,若由属性进行细化操作“∧”,得到一个新的形式背景∧K,则基于∧K可以得到更细粒度的形式概念.
证明:由定义9易知性质1成立.
性质2.给定形式背景K,若由属性进行细化操作“∧”,得到一个新的形式背景∧K,则|B(K)|≤|B(∧K)|,其中|B(K)|表示形式概念B(K)的基数.
证明:因为属性细化,属性个数增加,对应的形式概念个数也增加,所以细化后的形式背景得到的形式概念数量要多于细化前的形式背景得到的形式概念数量.
定义10.给定形式背景K=(G,M,I),G={g1,g2,…,gn}是非空有限对象集,M={m1,m2,…,mr}是非空有限属性集,设属性集Q={mi1,mi2,…,miq},q≥2,Q⊆M.若Q中的属性可以泛化一个属性mq,则∨{mi1,mi2,…,miq}=mq,记泛化后的形式背景为∨K=(G,∨M,∨I),∨M=(M-Q)∪mq.∨I和I之间通常具有下述两种约束关系:
1)∀g∈G,若∃mis∈Q,满足(g,mis)∈I,则(g,mq)∈∨I.
2)∀g∈G,若∀mis∈Q,满足(g,mis)∈I,则(g,mq)∈∨I.
在实际应用中,∨I和I之间的约束关系,可根据实际应用的需要灵活选择,本文采用约束关系(1).
定义11.形式背景K=(G,M,I),经属性集Q={mi1,mi2,…,miq},q≥2,Q⊆M,泛化为属性mq得到形式背景∨K,则∀(A,B)∈B(K),若B∩Q=∅,则(A,B)∈B(∨K);若B∩Q≠∅,则(A,B)在B(∨K)中表示为概念(((B-(B∩Q))∪mq)I,((B-(B∩Q))∪mq)).
下面给出一些性质说明K和∨K的关系.
性质3.给定形式背景K,若由属性进行细化操作“∨”,得到一个新的形式背景∨K,则基于∨K可以得到更粗粒度的形式概念.
证明:由定义11易知性质3成立.
性质4.给定形式背景K,若由属性进行泛化操作“∨”,得到一个新的形式背景∨K,则|B(∨K)|≤|B(K)|,其中|B(K)|表示形式概念B(K)的基数.
证明:因为属性泛化,引起属性个数减少,使得对应的形式概念个数也减少,所以泛化后的形式背景得到的形式概念数量要小于细化前的形式背景得到的形式概念数量.
下面通过例子说明形式概念分析中,属性细化和属性泛化的方法.
例2.基于表2给出的形式背景K,如果把属性b特长细化为唱歌特长b1和体育特长b2,则可以得到新的形式背景K1如表3所示.
表3 属性细化后的形式背景
Table 3 Formal context of attribute refinement

Gab1b2cs11010s20011s31100s40101s50001
对于表3的形式背景,由文献[6]可计算出形式概念:B(K1)={({s1,s2},{b2}),({s1,s3},{a}),({s3,s4},{b1}),({s2,s4,s5},{c}),({s1},{a,b2}),({s2},{b2,c}),({s3},{a,b1}),({s4},{b1,c}),({s1,s2,s3,s4,s5},{}),({},{a,b1,b2,c})}.
通过比较B(K1)和B(K)中的形式概念集合,可见属性细化后,可以得到更细的概念集合,从而提高问题分析的精度.反之,如果初始给定的形式背景K如表3所示,为了提高问题分析的效率,可以将属性唱歌特长b1和体育特长b2泛化为属性b特长,则得到新的形式背景∨K如表2所示.属性泛化后,可以得到更粗的形式概念.由文献[17]知,属性个数减少,构造形式概念时间减少,从而提高问题分析的效率.
注:属性细化和属性泛化的结果并不是唯一的,只需满足定义8或定义10中的约束关系即可.
3.2 属性分类的多层次形式概念动态构造算法
给定一个形式背景,当由于属性细化或泛化产生新的形式背景时,将有两种方式计算新的形式背景下的形式概念.第一种是完全基于新的形式背景重新计算所有的形式概念(即传统的渐进式构造算法[17]),该方法没有利用已有形式概念进行计算,对更新后的数据进行重新计算,相对而言,计算效率较低.另一种方法是结合原形式背景的形式概念,只针对细化或泛化的属性进行计算,减少了计算时间,即动态计算形式概念.
本节给出当属性细化或泛化产生新的形式背景时,动态构造形式概念算法.
算法1.形式概念动态构造算法
Input:形式概念集B(K),待细化(泛化)的属性集M1={b1,b2,…,bm},细化(泛化)后的属性集M2={m1,m2,…,mn},经属性细化(属性泛化)后的形式背景K′=(G,M′,I′).
Output:属性细化(属性泛化)后的形式概念集B(K′).
Step1.定义临时的形式概念集B(K*)=∅.
Step2.Foreach(A,B)∈B(K)
B′=B∩M1;
IfB′≠∅
B(K)=B(K)-(A,B);//去除概念(A,B)
If(B-B′)≠∅
B(K*)=B(K*)∪(A,B-B′);//添加(A,B-B′)
Endforeach
Step3.Foreach(A′,B′)∈B(K*)
If∀(A,B)∈B(K),满足B≠B′
B(K)=B(K)∪(A′,B′);
Endforeach
Step4.Foreachmj∈M2
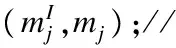
Foreach(A,B)∈B(K)

ElseifA⊆mI
B(K)=(B(K)-(A,B))∪(A,B∪m);
Elseif∀(A′,B′)∈B(K)&&(A′,B′)≠
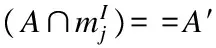
B(K)=B(K)∪(A′,B′∪m);
Endforeach
Endforeach
Step5.将B(K′)=B(K)&&
B(K′)=B(K′)-({},B-M1)+({},B-M1+M2)
输出B(K′).
假设形式背景中有l个对象,n个属性,通过文献[17]渐进式生成概念的算法构造的形式概念个数为N(N<=2n-1-1),若将k1(k1 注:引入临时的形式概念集B(K*)的目的是为了减少遍历次数,提高计算效率. 例3.给定细化前的形式背景K如表2所示.经属性细化得到的形式背景K1如表3所示.按照算法1的步骤给出属性细化时,形式概念动态构造算法的详细计算过程如下所示. Input:经属性细化得到的形式背景K1如表3所示.由形式 背景K得到的形式概念B(K)={({s1,s3},{a,b}),({s1,s2,s3,s4},{b}),({s2,s4},{b,c}),({s2,s4,s5},{c}),({},{a,b,c}),({s1,s2,s3,s4,s5},{})},待细化的属性集M1={b},细化后的属性集M2={b1,b2}. Output:最终的形式概念B(K′). Step1.定义临时的形式概念B(K*)=∅. Step2.依次取B(K)中的概念进行处理: ①.概念({s1,s3},{a,b}) 处理结果是:B(K*)添加({s1,s3},{a}),B(K)删除({s1,s3},{a,b}). ②.概念({s1,s2,s3,s4},{b}) 处理结果是:B(K)删除({s1,s2,s3,s4},{b}). ③.概念({s2,s4},{b,c}) 处理结果是:B(K*)添加({s2,s4},{c}),B(K)删除({s2,s4},{b,c}). ④.概念({s2,s4,s5},{c}) 处理结果是:不变. ⑤.概念({},{a,b,c}) 处理结果是:B(K*)添加({},{a,c}),B(K)删除({},{a,b,c}). ⑥.概念({s1,s2,s3,s4,s5},{}) 处理结果是:不变. 此时B(K*),B(K)的结果是: B(K)={({s2,s4,s5},{c}),({s1,s2,s3,s4,s5},{})}. B(K*)={({s1,s3},{a}),({s2,s4},{}),({},{a,c})}. Step3.依次取B(K*)中的概念进行处理: ①.概念({s1,s3},{a}) 处理结果是:B(K)添加({s1,s3},{a}). ②.概念({s2,s4},{c}) 处理结果是:不变. ③.概念({},{a,c}) 处理结果是:B(K)添加({},{a,c}). 此时:B(K)={({s2,s4,s5},{c}),({s1,s2,s3,s4,s5},{}), ({s1,s3},{a}),({},{a,c})}. Step4.依次取M2={b1,b2}中的属性进行处理: 处理结果是:B(K)={({s2,s4,s5},{c}),({s1,s2,s3,s4,s5},{}),({s1,s3},{a}), ({s4},{c,b1}),({s3},{a,b1}),({},{a,c}),({s3,s4},{b1})}. 处理结果是:B(K)={({s2,s4,s5},{c}),({s1,s2,s3,s4,s5},{}),({s1,s3},{a}),({s4},{c,b1}),({s3},{a,b1}),({},{a,c}),({s3,s4},{b1}),({s1,s2}, {b2}),({s1},{a,b2}),({s2},{b2,c}). Step5.将B(K)赋值给B(K′)并修正B(K′),输出B(K′). B(K′)={({s2,s4,s5},{c}),({s1,s2,s3,s4,s5},{}),({s1,s3},{a}),({s4},{c,b1}),({s3},{a,b1}),({s3,s4},{b1}),({s1,s2},{b2}),({s1},{a,b2}),({s2},{b2,c}),({},{a,b1,b2,c}). 本节通过仿真实验,对比分析,当属性细化或泛化时,原有的形式背景自身数据发生变化.静态的形式概念构造算法(即传统的渐进式算法[17])和动态的形式概念构造算法的运行时间对比.通过实验验证了本文所提算法的有效性. 由于形式概念计算中数据值较单一,且现有的形式概念算法的研究多以人工生成方式做为实验数据.本章的仿真实验数据生成如下:首先指定形式背景的对象个数、属性个数以及对象属性关联的概率(指属性值非0个数的比率),然后由程序自动生成实验数据.例如,假定对象个数为100,属性个数为10,对象属性关联概率是30%,表示数据集中非0的属性值个数有300个.而本实验中将设定对象的个数为200,属性的个数为50,对象属性关联概率选择33%,从而生成一个形式背景,用K′表示,并对形式背景K′进行实验. 实验平台为:windows7操作系统、Intel(R)Core(TM)i3CPU3.20GHz、2G内存的微机.在Eclipse中用Java语言编程实现. 针对形式背景K′,通过属性细化和属性泛化方法,分别进行实验.对于属性细化的情况,考虑单个属性细化和多个(组)属性细化两种情况.所谓单个属性细化是指,每次只考虑将一个属性细化为若干个属性, 考虑到实际情况和实验研究的意义,单个属性细化最多设为10个.实验中分别设置将一个属性细化为2个属性、3个属性、….、10个属性,对形式背景K′分别进行单个属性细化实验,结果如图1所示.其中横轴表示单个属性细化后的属性个数,纵轴表示运行时间(单位为毫秒).所谓多个属性细化是指,每次考虑将多个属性同时细化为若干个属性,如同时将两组属性进行细化、同时将三组属性进行细化,考虑到实际情况和实验研究的意义,多个属性细化最多设为20组.实验中分别设置同时细化的属性组数为2组、4组、6组、…、20组.为了简化操作,对于多个属性细化,我们仅考虑将每组属性细化为两个属性的情况,即若同时将16组属性进行细化,那么原有的形式背景中的16个属性将变成32个新的属性,对形式背景K′分别进行多个属性细化实验,结果如图2所示.其中横轴表示同时细化的属性个数,纵轴表示运行时间(单位为毫秒).针对属性泛化的情况,考虑单组属性泛化和多组属性泛化两种情况.所谓单组属性泛化是指,每次只考虑将若干个属性泛化为一个属性,考虑到实际情况和实验研究的意义,单个属性泛化最多设为10个.实验中分别设置泛化的属性个数为2个、3个、…、10个,对形式背景K′分别进行单个属性泛化实验,结果如图3所示.其中横轴表示泛化的属性个数,纵轴表示运行时间(单位为毫秒).所谓多组属性泛化是指,每次考虑将多组属性分别泛化为若干个属性,如同时将两组属性分别泛化为两个属性,同时将三组属性分别泛化为两个属性,考虑到实际情况和实验研究的意义,多个属性泛化最多设为20组.实验中设置同时泛化的属性的组数为2组、4组、6组、…、20组.为了简化操作,对于多组属性泛化,我们仅考虑将两个属性泛化为一个属性的情况,即若同时将16组属性进行泛化,那么原有的形式背景中这16个属性将变成8个新的属性,对形式背景K′分别进行多个属性泛化实验,结果如图4所示.其中横轴表示属性泛化的组数,纵轴表示运行时间(单位为毫秒). 图1 单个属性细化实验比较Fig.1 Comparison of single attribute refinement experiments 图2 多组属性细化实验比较Fig.2 Experimental comparison of multiple attribute refinement 从图1中可以看出,对于“单个属性细化”,动态的形式概念构造算法花费的时间明显少于静态的形式概念构造算法.关于静态的形式概念构造算法和动态的形式概念构造算法的运行时间,随着细化后子属性个数的增加,两者都是呈现单调上升的趋势.这是因为属性细化后,属性个数增加导致运行时间增加. 从图2中可以看出,对于 “多组属性细化”,动态的形式概念构造算法花费的时间明显少于静态的形式概念构造算法.关于静态的形式概念构造算法和动态的形式概念构造算法的运行时间,随着细化后子属性组数的增加,两种呈现出先上升后下降的趋势.原因是:虽然属性细化后,属性个数增加导致运行时间增加,但是细化后的每个属性中对象特征(属性)关联概率降低(按照定义8中的约束(1)),运行时间减少,在这两者的相互作用下,反而呈现下降的趋势,图1中呈现单调上升,是由于对象特征关联概率降低对单个属性细化影响较小. 图3 单个属性泛化实验比较Fig.3 Comparison of single attribute generalization 从图3中可以看出,对于“单个属性泛化”,动态的形式概念构造算法花费的时间都明显少于静态的形式概念构造算法.需要注意的是图3中,静态的形式概念构造算法和动态的形式概念构造算法的运行时间,随着泛化后属性个数的减少,两者呈现单调下降的趋势.这是因为属性泛化后,属性个数减少会导致运行时间减少. 图4 多组属性泛化的实验比较Fig.4 Experimental comparison of multiple attribute generalization 从图4中可以看出,对于“多组属性泛化”,动态的形式概念构造算法花费的时间都明显少于静态的形式概念构造算法.关于静态的形式概念构造算法和动态的形式概念构造算法的运行时间,随着泛化后属性个数的减少,两者呈现出先上升后下降的趋势,这是因为虽然属性泛化后,属性个数减少会导致运行时间减少,但是泛化后的每个属性中对象特征(属性)关联概率增大(按照定义10中的约束(1)),运行时间增加,在这两者的相互作用下,没有呈现出严格的单调下降.而图3中呈现单调下降,是由于对象特征关联概率增加对单个属性泛化影响较小. 通过以上实验证明了本文提出的基于属性分类多层次的形式概念动态构造算法的有效性.因为静态的形式概念构造算法总是将所有的数据重新计算,而动态的形式概念构造算法是利用原有的形式概念数据基础上对自身变化的数据进行动态的更新,所以动态的形式概念构造算法处理的数据较少.因此,基于属性分类(属性细化和属性泛化)变化的形式概念,动态的形式概念构造算法更有效. 从粒计算的角度分析,现有的形式概念分析所研究的属性大多是单粒度单层次的,忽视了在实际应用中,属性具有不同的粒度层次,基于形式背景构造形式概念时,根据实际问题的求解需要,将粗粒度属性细化为两个或多个细粒度属性,可以提高问题分析的精度,将两个或多个细粒度属性泛化为粗粒度属性,可以提高问题分析的效率.所以,本文给出了属性分类的属性泛化与细化方法,实现了形式概念在不同层次泛化空间下相关性质.在此基础上,提出了属性分类的多层次形式概念动态构造算法,该算法通过自学习的方式对原有的知识加以使用,它不仅继承了渐进式算法的优点,还实现了形式概念自身数据的变化. [1] Wille R.Concept lattices and conceptual knowledge systems[J].Computers & Mathematics with Applications,1992,23(6-9):493-515. [2] Ignatov D I,Gnatyshak D V,Kuznetsov S O,et al.Triadic formal concept analysis and triclustering:searching for optimal patterns[J].Machine Learning,2015,101(1-3):271-302. [3] Codocedo V,Lykourentzou I,Napoli A.A semantic approach to concept lattice-based information retrieval[J].Annals of Mathematics & Artificial Intelligence,2014,72(1-2):169-195. [4] Sridhar M,Gill NS.A formal conceptual framework for dynamics within context of component-based system for designing robust software systems & metrics[J].International Journal of Software Engineering & Applications,2015,6(2):21-31. [5] Yao J,Vasilakos A V,Pedrycz W.Granular computing:perspectives and challenges[J].Cybernetics IEEE Transactions on,2013,43(6):1977-1989. [6] Li J,Mei C,Xu W,et al.Concept learning via granular computing:a cognitive viewpoint[J].Information Sciences,2015,298(1):447-467. [7] Qu Kai-she,Zhai Yan-hui,Liang Ji-ye,et al.Representation and extension of rough set theory based on formal concept analysis[J].Journal of Software,2007,18(9):2174-2182. [8] Zhang Lei,Zhang Hong-li,Yin Li-hua,et al.Theory and algorithms of attribute decrement for concept lattice[J].Journal of Computer Research & Development,2013,50(2):248-259. [9] Qian Y H,Zhang H,Sang Y L,et al.Multigranulation decision-theoretic rough sets[J].Int J of Approximate Reasoning,2014,55(1):225-237. [10] Ganter B,Wille R.Formal concept analysis:mathematic foundations[M].Berlin:Springer-Verlag,1999:17-58. [11] Singh P K,Kumar C A,Li J.Knowledge representation using interval-valued fuzzy formal concept lattice[J].Soft Computing,2016,20(4):1485-1502. [12] Wang Xing-xing,Zhang Ji-fu,Zhang Su-lan.A batch constructing algorithm of frequent weighted concept lattice[J].Pattern Recognition and Artificial Intelligence,2010,23(5):678-685. [13] Li-Ping Q U.Attribute-based fast incremental algorithm for building relative reduced concept lattice[J].Computer Science,2008,35(4):135-138. [14] Zhi Hui-lai,Zhi Dong-jie.Theory and algorithm of concept lattice incremental construction based on attributes[J].Computer Engineering and Applications,2012,48(26):17-21. [15] Zou L,Zhang Z,Long J,et al.A fast incremental algorithm for deleting objects from a concept lattice[J].Knowledge-Based Systems,2015,89(C):411-419. [16] Liu Zong-tian,Qiang Yu,Zhou Wen,et al.A fuzzy concept lattice model and its incremental construction algorithm[J].Chinese Journal of Computers,2007,30(2):184-188. [17] Zou L,Zhang Z,Long J.A fast incremental algorithm for constructing concept lattices[J].Expert Systems with Applications,2015,42(9):4474-4481. 附中文参考文献: [7] 曲开社,翟岩慧,梁吉业,等.形式概念分析对粗糙集理论的表示及扩展[J].软件学报,2007,18(9):2174-2182. [8] 张 磊,张宏莉,殷丽华,等.概念格的属性渐减原理与算法研究[J].计算机研究与发展,2013,50(2):248-259. [12] 王欣欣,张继福,张素兰.一种频繁加权概念格的批处理构造算法[J].模式识别与人工智能,2010,23(5):678-685. [14] 智慧来,智东杰.基于属性的概念格渐进式构造原理与算法[J].计算机工程与应用,2012,48(26):17-21. [16] 刘宗田,强 宇,周 文,等.一种模糊概念格模型及其渐进式构造算法[J].计算机学报,2007,30(2):184-188.
4 仿真实验
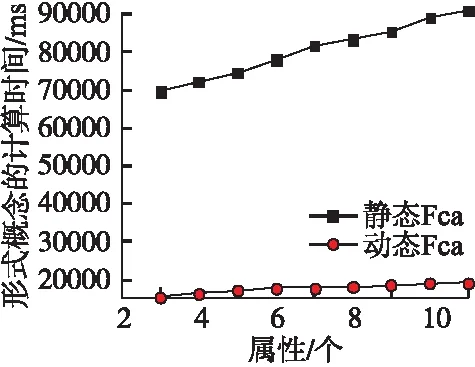

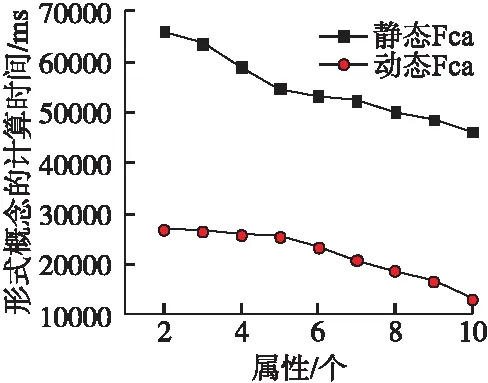
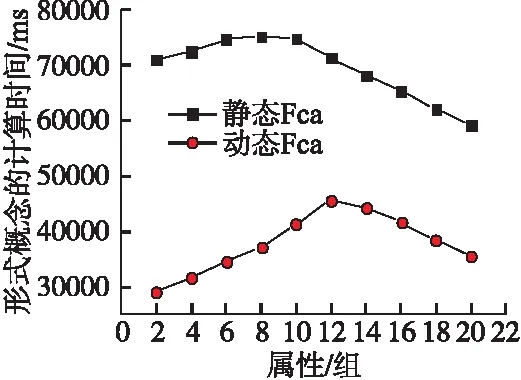
5 结 论

