一种SOFM网络的二阶段聚类算法

丁天一,张 旻

(电子工程学院,合肥 230037)

1 引 言

聚类是数据挖掘、模式识别等研究方向的重要研究内容之一,在识别数据的内在结构方面具有极其重要的作用.作为一种有效的数据分析方法,聚类已经广泛地用于语音识别、图像处理、信息检索和统计科学等领域[1,2].随着人类获取数据的手段越来越多,数据正以前所未有的速度增长和累积,人们对于聚类的要求也越来越高.一般的聚类算法,如k-means算法[3]、k-medoids算法[4]等,需要预先指定一个聚类数目,然而在实际应用过程中聚类数目往往是未知的,因此寻求一种有效的在聚类数目未知情况下完成聚类的算法成为了一个亟待解决的问题[5].

目前为止有不少学者针对聚类数目未知情况下的聚类问题进行研究,并提出了一些算法与聚类有效性评价指标以确定最佳聚类数目.文献[6]提出了一种基于层次划分的最佳聚类数确定方法COPS,用于自动确定大型、复杂数据集的最佳聚类数目,但是控制计算精度参数的取值可能会对计算结果产生影响;文献[7]提出了一种基于人工免疫的自适应谱聚类算法,通过模拟抗体的克隆选择机制和免疫系统的初次免疫应答、二次免疫应答机制,实现数据样本聚类分组数的自动调整,但是算法中的阈值参数需要多次实验确定,阈值不同实验结果也有较大差异;文献[8]提出了一种k-means算法的最佳聚类数确定算法,通过样本数据分层得到聚类数搜索范围的上界,并设计了一种聚类有效性指标评价聚类后类内与类间相似性程度以获取最佳聚类数,但是聚类有效性指标不能保证对于每种数据集都能得到一个正确的聚类数目.文献[9]提出了一种基于局部密度下降搜索的自适应聚类算法,但需要人为设置多种参数,迭代搜索过程使聚类耗时较大.文献[10]提出了一种谱聚类最佳聚类数的确定方法,结合了Silhouette评价指标与局部尺度的概念,但实验中的参数设置较为复杂,算法复杂度较高.自组织特征映射网络是一种无监督聚类算法,由于无需指定聚类数目,具有自组织学习特性,适用于高维数据聚类等优点,而广泛应用于聚类问题中[11-13].但SOFM网络训练结束后存在大量的获胜神经元,远多于实际样本类别数.因此,如何有效地利用SOFM网络的学习结果并确定样本最佳聚类数,对解决未知聚类数目情况下的聚类问题具有重要的意义[14].

鉴于此,本文提出了一种SOFM网络的二阶段聚类算法,实现在聚类数目未知的情况下对数据的聚类.该算法包含两个阶段:首先通过SOFM网络的无监督自组织学习过程将数据集划分成若干个子类,每一个子类用获胜神经元代表该类内的所有样本;然后采用凝聚层次聚类的方法对获胜神经元进行聚类,并以树状图的形式表示聚类结果;最后,综合两次聚类结果,将获胜神经元的聚类结果映射到原始数据集,得到最终聚类结果.该算法无需任何先验知识,解决了SOFM网络学习结束后获胜神经元较多的问题的同时,充分利用了SOFM网络的自组织学习特性,结合了层次聚类算法的优点,适合于聚类数目未知情况下数据的聚类,提高了聚类准确率和稳定性.

2 SOFM网络模型

SOFM网络是由输入层和输出层(竞争层)组成的两层神经网络.输入层是一维的神经元,有n个节点,节点数n与输入样本向量的维数相同.输出层是二维神经元,按二维形式排列成节点矩阵,有m=p×q个节点.SOFM网络中有两种连接权值,即输入神经元与输出神经元之间的连接权值以及输出神经元的侧向连接权值[15].SOFM网络的二维平面阵列模型如图1所示.

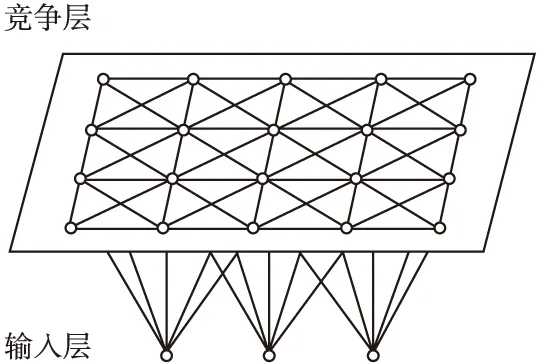
图1 SOFM网络模型Fig.1 SOFM model

SOFM网络是一种无监督聚类法,其能将任意输入模式在输出层映射成一维或二维离散图形,并保持其拓扑结构不变,即通过对输入样本的自组织学习,在输出层将分类结果表示出来.此外,网络通过对输入模式的反复学习,可以使连接权值空间分布密度与输入模式的概率分布趋于一致,即连接权向量空间分布能反映输入模式的统计特征.

在输入样本类数未知的情况下,构造SOFM网络时要求输出层神经元的数量足够多,造成了训练结束后网络的输出层存在大量的获胜神经元,而实际中样本的类数远远小于获胜神经元的数目.很多获胜神经元权值十分接近,这些神经元所代表的是同一个类别的样本,将权值相近的神经元所代表的样本合并可以获得更优的聚类结果.

3 SOFM网络的二阶段聚类算法

SOFM网络的二阶段聚类算法主要分为SOFM网络对数据集的粗聚类过程和层次聚类对获胜神经元的细聚类过程两部分.在对输入样本进行数据预处理之后,通过SOFM网络的自组织学习过程将样本分为若干个簇,以获胜神经元代表每一个簇内的所有样本.下一步,通过层次聚类的方法,对获胜神经元进行聚类,将同一类别神经元对应的所有样本合并,得到最终的聚类结果.

3.1 数据预处理

在数据集输入到SOFM网络的输入层之前,需要对数据进行规范化处理以适用于SOFM网络的学习过程,本文采用如下的归一化(最小-最大规范化)处理方式:

(1)

3.2 基于SOFM网络的粗聚类

SOFM网络采用Kohonen学习规则,总结起来主要分为两步:第一,寻找最优匹配神经元,即竞争学习过程;第二,更新权值的自适应调整过程,即输出层神经元的侧反馈过程.具体步骤如下:

Step1.网络初始化.初始化权值wij(0),(i=1,2,…,n;j=1,2,…,m),赋予wij(0)一个[0,1]区间内的随机值.初始化设置各输出神经元j的邻域初始值NEj(0).确定学习速率的初始值γ(0)(0<γ(0)<1)和总的学习次数K.

Step2.寻找样本向量的最优匹配神经元.提供一个新的样本向量作为网络的输入,计算输入向量与所有输出层神经元之间的欧氏距离dj,并求出dj*满足式(2)条件下的输出层神经元j*(j*∈[1,m]).

(2)

Step3.调整连接权值.修正输出神经元j*与其邻域内其他神经元与输入层神经元之间的连接权值:

wij(k+1)=wij(k)+γ(k)(xj-wij(k))

(3)

式(3)中,j∈NEj*(k),i∈[1,n],γ(k)为第k次学习时的学习速率.

返回Step 2,直至输入向量全部提供给网络.

Step4.更新学习速率γ(k)及邻域NEj(k):

(4)

(5)

式(4)和式(5)中,γ(0)为学习速率的初始值,NEj(0)为邻域NEj(k)的初始值,INT(x)为取整符号,k为学习次数,K为总的学习次数.

令k=k+1,返回Step 2,直至k=K迭代结束.

假设M为输入样本向量的数量,即数据集的样本个数为M,通过上述的学习过程,最终学习后的网络将样本数据划分成C类,即:

(6)

式(6)中,C表示获胜神经元的数目,D1,D2,…,DC表示样本数据的粗聚类结果.

3.3 基于凝聚层次聚类的细聚类

SOFM网络对样本向量自组织学习,得到了样本数据的粗聚类结果,输出层的网格中以获胜神经元权值分布的形式保存了输入样本的分布与拓扑信息.通过对学习后的神经元权值进行聚类,可得到进一步的细聚类结果.学习结束后神经元权值分布往往是不规则的,本文采用凝聚层次聚类方法对神经元权值进行聚类.凝聚层次聚类是一种采用自底而上聚合策略的层次聚类算法,以单个数据对象为初始簇,最近簇相聚和的方法融合,直至得到期望的聚类数为止[16].

假定有N个对象要被聚类,构造N×N的相似矩阵D=d(i,j),聚类结果用序号0,1,…,n-1表示,L(m)表示第m次聚类的层次.簇的序号用m表示,簇r和簇s的相似系数(即相似矩阵中的值)用d(r,s)表示.

层次聚类在构造相似度矩阵的过程中有很多种距离的度量方法,本文选取了Ward′s method(离差平方和)的距离度量方法,将簇间的距离d(r,s)定义为两个簇合并时产生的误差平方和:

(7)

基于最小距离的凝聚层次聚类算法描述如下:

Step1.L(0)=0,m=0.

Step2.从当前所有簇对中,根据d(r,s)=mind(i,j)找到距离最近的两个簇r,s.

Step3.簇的序列号加1,即m=m+1,将簇r和簇s合并,令聚类的层次L(m)=[d(r,s)].

Step4.更新相似矩阵D,删除簇r,s相应的行和列,并在矩阵中加上新生成的簇相应的行和列.相似矩阵中新生成的簇(r,s)和原来的簇k的相似度由下式定义:

d(k,(r,s))=min(d(k,r),d(k,s))

(8)

Step5.重复Step 2～Step 4,直到所有对象都被合并到一个簇为止.

凝聚层次聚类算法一直执行到所有样本出现在同一个簇中,以“树状图”的形式表示聚类结果,其中每层链接一组聚类簇.在树状图的特定层次上进行分割,可得到相应的簇划分结果.

4 实验结果与分析

为了验证SOFM网络的二阶段聚类算法的性能,本文设计了两个实验.实验1通过模拟一组分布杂乱的人工数据集来验证SOFM网络的二阶段聚类算法过程的可行性,实验2从UCI数据集中选取3种典型的数据集,分别用k-means算法、层次聚类算法、基于U-Matrix可视化分析的SOFM网络聚类算法和SOFM网络的二阶段聚类算法对数据集进行聚类实验,通过比较四种聚类算法的正确率验证本文算法的有效性.

4.1 人工数据集仿真实验

为了验证SOFM网络的二阶段聚类算法过程的可行性,实验参照文献[7]的方法随机生成一组服从正态分布的二维模拟数据,共包含140个样本,生成人工数据集的参数如表1所示.其中,μx、μy为用于生成正态分布数据的均值,σ为标准差.

首先,采用k-means算法对人工数据集进行聚类实验,选取聚类数目k=5时得到的4次聚类结果如图2所示.

由图2可以看出,当数据集的分布较为接近时,即便是在指定聚类数目k的情况下,由于k-means算法聚类初始中心的不确定性,也会造成重复实验过程中聚类结果的多样性,且不同聚类结果差别较大.

表1 人工数据集的参数值
Table 1 Parameter value of artificial datasets

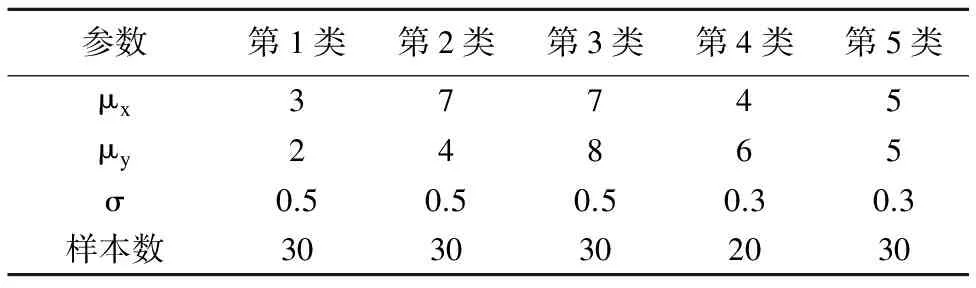
参数第1类第2类第3类第4类第5类μx37745μy24865σ0．50．50．50．30．3样本数3030302030

下一步,采用本文的算法对人工数据集进行聚类实验.在建立SOFM网络时,输出层二维映射神经元的节点矩阵采用10×10的排列形式,拓扑结构采用六边形结构,学习次数设置为500.将归一化处理后的人工数据集输入到SOFM网络的输入层,学习结束后得到的输出层结果如图3所示.

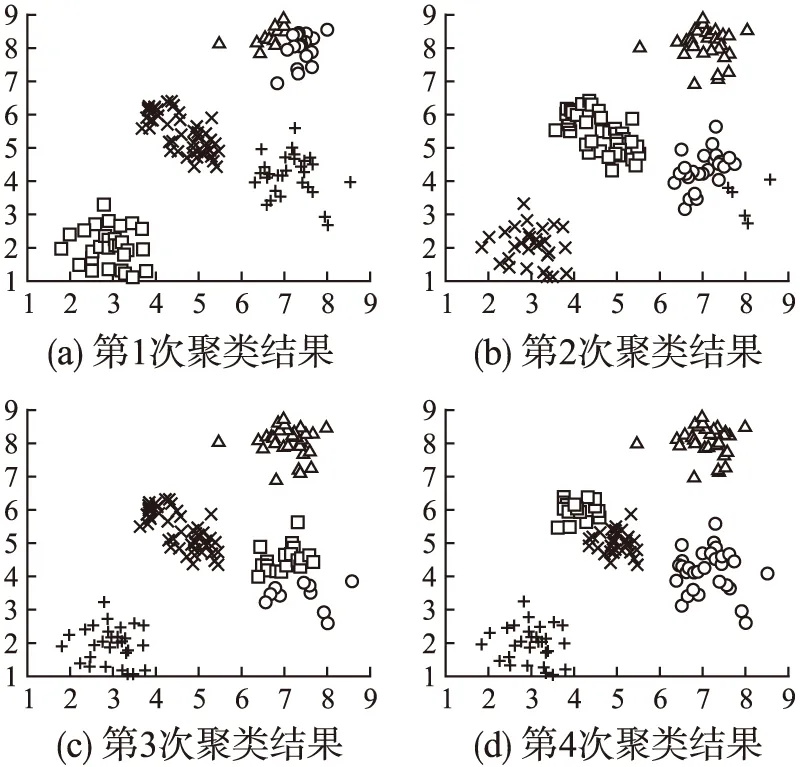
图2 k-means算法聚类结果Fig.2 Clustering results of k-means algorithm

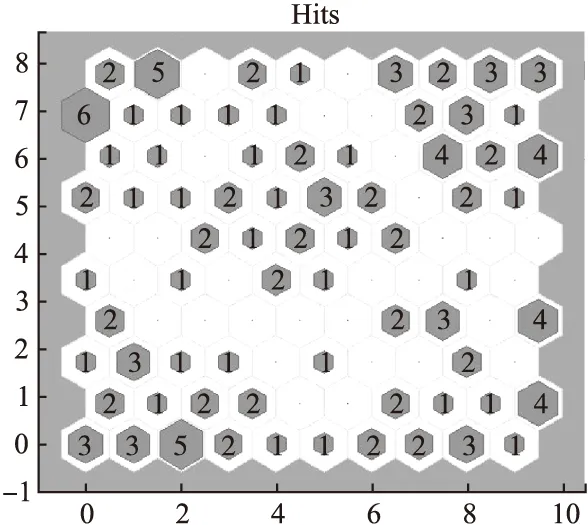
图3 学习结束后的输出层结果Fig.3 Result of the output layer after learning

通过SOFM网络对样本的学习,网格中保存了输入样本的分布与拓扑信息.在输出层的100个神经元中,有71个获胜神经元,每一个网格中的数字表示获胜神经元所代表的样本数目.实验中SOFM网络将输入样本分为71类,每一类只代表少量的样本,此时SOFM网络的学习结果作为人工数据集的粗聚类结果.

采用凝聚层次聚类对SOFM网络学习后的神经元权值进行聚类,通过对层次聚类树状图的观察分析以确定一个合适的聚类数,实验结果如图4所示,从树状图中可以得到簇与簇之间的连接关系与相似度.

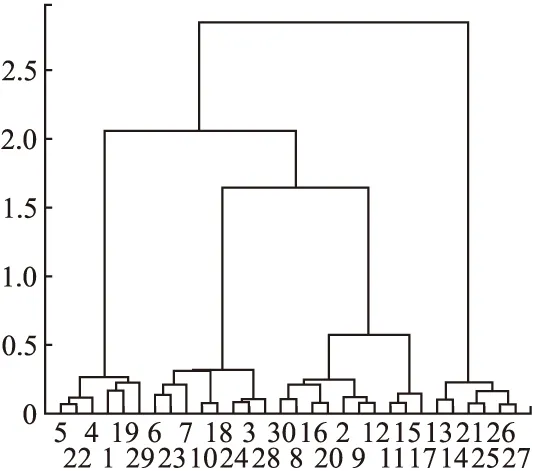
图4 获胜神经元的聚类树状图Fig.4 Clustertree of the winning neuron

通过图4可以看出,当聚类数目k=5时,聚类所得到的簇与簇之间的距离较大,此时神经元权值能得到最佳的聚类结果.选取聚类数目k=5时,综合二阶段过程的聚类结果,得到人工数据集的聚类结果如图5所示.

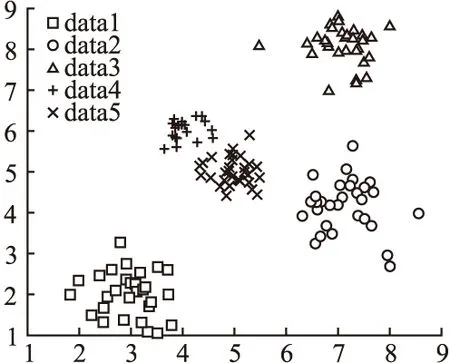
图5 人工数据集聚类结果Fig.5 Clustering result of artificial datasets

从图5可以看出,在人工数据集仿真实验中,SOFM网络的二阶段聚类算法可以提供一个合适的聚类数目,并且能够准确地划分数据.

4.2 UCI数据集仿真实验

为了验证SOFM网络的二阶段聚类算法对于复杂分布数据的有效性,实验选取了UCI数据集中的Iris、Wine和Pima Indians Diabetes作为实验的数据集,数据集属性特征如表2所示.

表2 UCI数据集属性特征
Table 2 Attribute feature of UCI dataset

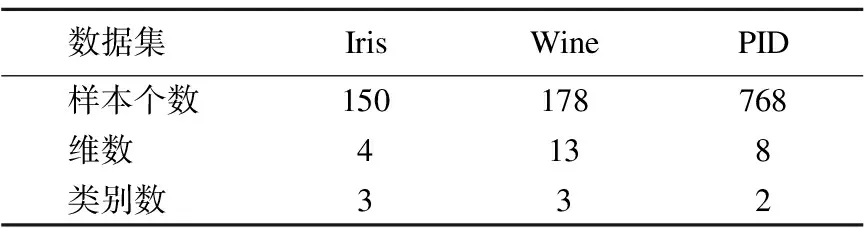
数据集IrisWinePID样本个数150178768维数4138类别数332

实验中分别用k-means算法、Single-linkage层次聚类算法、基于U-Matrix可视化分析的SOFM网络聚类算法和本文算法对以上数据集进行聚类实验,通过数据集聚类结果的正确率指标来比较四种算法的性能,聚类正确率定义为:

(9)

由于SOFM网络的自组织学习特性以及k-means算法初始中心点选取的随机性,实验中对每种算法在每个UCI数据集上分别进行50次实验,实验得到的四种聚类算法求解UCI数据集的聚类正确率的平均值如表3所示.

表3 四种算法在求解UCI数据集时的性能比较
Table 3 Performance comparison of four algorithms in solving the UCI datasets

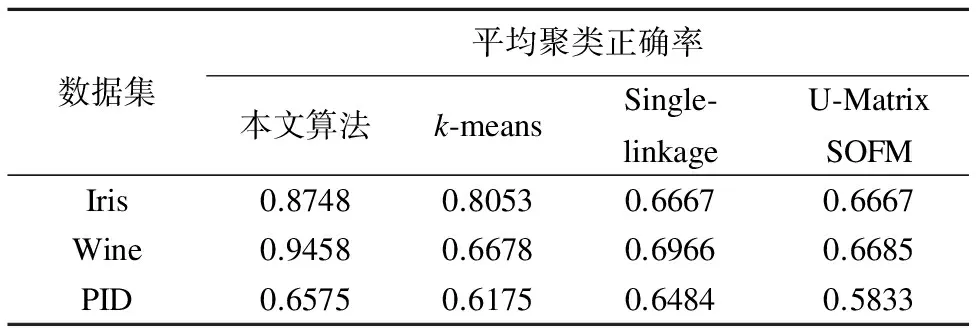
数据集平均聚类正确率本文算法k⁃meansSingle⁃linkageU⁃MatrixSOFMIris0．87480．80530．66670．6667Wine0．94580．66780．69660．6685PID0．65750．61750．64840．5833

由表3的统计结果可以看出,本文提出的算法在对三组UCI数据集进行的聚类实验过程中取得了较好的聚类结果,聚类结果的正确率均高于其他算法.因此,本文提出的算法对于复杂分布数据的聚类是有效的.

5 结束语

本文通过对SOFM网络自组织学习特性的分析,结合层次聚类算法,提出了一种SOFM网络的二阶段聚类算法.在粗聚类阶段,通过SOFM网络的自组织学习过程,得到以获胜神经元为代表的若干个簇;在细聚类阶段,通过凝聚层次聚类的方法,对获胜神经元进行再聚类;最后综合两阶段的聚类结果,得到数据集最终的聚类结果.通过人工数据集和UCI数据集验证了本文算法的可行性与有效性,实验结果表明,SOFM网络的二阶段聚类算法具有较高的准确率,可以在聚类数目未知的情况下较好地完成数据的聚类.

[1] Han Jia-wei,Kamber Micheline,Pei Jian.Data mining:concepts and techniques[M].Beijing:China Machine Press,2012.

[2] Sun Ji-gui,Liu Jie,Zhao Lian-yu.Clustering algorithms research[J].Journal of Software,2008,19(1):48-61.

[3] Hartigan J A,Wong M A.A k-means clustering algorithm[J].Applied Statistics,1979,28(1):100-108.

[4] Park H S,Jun C H.A simple and fast algorithm for k-medoids clustering[J].Expert Systems with Applications,2009,36(2):3336-3341.

[5] Wang Jun,Wang Shi-tong,Deng Zhao-hong.Survey on challenges in clustering analysis research[J].Control and Decision,2012,27(3):321-328.

[6] Chen Li-fei,Jiang Qing-shan,Wang Sheng-rui.A hierarchical method for determining the number of clusters[J].Journal of Software,2008,19(1):62-72.

[7] Guo Kai,Li Hai-fang,Wang Hui-qing.An adaptive spectral clustering algorithm based on artificial immune[J].Journal of Chinese Computer Systems,2013,34(4):856-859.

[8] Wang Yong,Tang Jing,Rao Qin-fei,et al.High efficient k-means algorithm for determining optimal number of clusters[J].Journal of Computer Applications,2014,34(5):1331-1335.

[9] Xu Zheng-guo,Zheng Hui,He Liang,et al.Self-adaptive clustering based on local density by descending search[J].Journal of Computer Research and Development,2016,53(8):1719-1728.

[10] Mur A,Dormido R,Duro N,et al.Determination of the optimal number of clusters using a spectral clustering optimization[J].Expert Systems with Applications,2016,65(23):304-314.

[11] Stephanakis I M,Anastassopoulos G C,Iliadis L.A self-organizing feature map(SOFM)model based on aggregate-ordering of local color vectors according to block similarity measures[J].Neuro Computing,2013,107(4):97-107.

[12] Huang C H,Lin C H.Multiple harmonic-source classification using a self-organization feature map network with voltage-current wavelet transformation patterns[J].Applied Mathematical Modelling,2015,39(19):5849-5861.

[13] Li N,Cheng X,Zhang S,et al.Realistic human action recognition by fast HOG3D and self-organization feature map[J].Machine Vision and Applications,2014,25(7):1793-1812.

[14] Brugger D,Bogdan M,Rosenstiel W.Automatic cluster detection in Kohonen′s SOM[J].IEEE Transactions on Neural Networks,2008,19(3):442-459.

[15] Wu S,Chow T W S.Clustering of the self-organizing map using a clustering validity index based on inter-cluster and intra-cluster density[J].Pattern Recognition,2004,37(2):175-188.

[16] Zhou Chen-xi,Liang Xun,Qi Jin-shan.A semi-supervised agglomerative hierarchical clustering method based on dynamically updating constraints[J].Acta Automatica Sinica,2015,41(7):1253-1263.

附中文参考文献：

[1] Han Jia-wei,Kamber Micheline,Pei Jian.数据挖掘:概念与技术[M].北京:机械工业出版社,2012.

[2] 孙吉贵,刘 杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.

[5] 王 骏,王士同,邓赵红.聚类分析研究中的若干问题[J].控制与决策,2012,27(3):321-328.

[6] 陈黎飞,姜青山,王声瑞.基于层次划分的最佳聚类数确定方法[J].软件学报,2008,19(1):62-72.

[7] 郭 凯,李海芳,王会青.一种人工免疫的自适应谱聚类算法[J].小型微型计算机系统,2013,34(4):856-859.

[8] 王 勇,唐 靖,饶勤菲,等.高效率的K-means最佳聚类数确定算法[J].计算机应用,2014,34(5):1331-1335.

[9] 徐正国,郑 辉,贺 亮,等.基于局部密度下降搜索的自适应聚类方法[J].计算机研究与发展,2016,53(8):1719-1728.

[16] 周晨曦,梁 循,齐金山.基于约束动态更新的半监督层次聚类算法[J].自动化学报,2015,41(7):1253-1263.