直线与二次曲线位置关系的安全判定协议
于金霞,赵翠平,张 静,汤永利
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
1 引 言
网络技术的迅猛发展为多方协作计算创造了大量的应用前景,但这些计算很可能发生在没有信任关系的参与者之间,个人隐私数据会被泄露或者篡改.安全多方计算[1](SMC)是信息社会隐私数据保护的核心技术,它是指两个或多个参与者能够在不泄露各自输入的隐私数据,并利用这些隐私数据参加保密计算,共同完成某项计算任务.安全多方计算在大数据安全与隐私保护、基因序列、数据挖掘、密钥分配、科学计算等方面应用广泛.
计算几何问题的保密计算(Privacy-Preserving Computional Geometry,PPCG)是安全多方计算的一个重要研究领域,最初是由Atallah等[2]提出.具体地说,PPCG问题的研究就是根据特殊应用设计出具体协议,在执行协议的过程中,参与方虽然可以使用对方的隐私数据,但不能知道对方的隐私数据.隐私保护的计算几何问题在实际应用中具有重要意义,已成为国际众多学者关注的热点问题之一.Du等[3]主要从线段相交、点包含、凸包以及多边形相交等方面研究了隐私保护的计算几何问题.Du[4]首次提出了二维空间上两条直线问题和凸包问题,不仅基于置换协议和安全两方点积协议给出了解决方案,而且给出了解决此类问题有用的知识模块,但是函数求值时可能产生信息泄露.文献[5]针对Du的算法进行了修改,但当用户输入的隐私数据需要得到保护时,对传统算法做简单改进也不能满足要求,对此提出半诚实模型下计算几何中关于线段最核心的算法—叉积协议.文献[6]针对Du的凸包问题,基于Paillier同态加密方案设计了安全两方线段求交协议,此协议通过求交点的坐标来判断两条线段是否相交,并给出恶意模型下的协议,保护隐私的凸包求交集协议首次实现了求解凸包并集时的隐私保护,并用Goldreich证明法证明了该协议是安全的.文献[7]针对Du的两线段相交计算复杂性高的问题提出一种高效的不经意传输协议,并将高效不经意传输协议扩展到判定两个任意多边形和两个任意几何图形相交问题.文献[2,8-11]研究了点包含问题,文献[2]中Atallah的协议只适用于一些简单多边形域,文献[8]研究的是点与圆域,文献[9]研究的是点与椭圆域,文献[10]研究的是点与凸多边形域.文献[11]针对协议本身的局限性和算法复杂度高的问题,提出了保护私有信息的点包含协议,该协议在效率上优于现有方案,并具有可扩展性,但还不能判断点和任意多边形的位置关系.由于文献[2,8-11]都具有特殊性,文献[12]利用角旋转法提出了保护隐私的任意多边形点包含两方计算协议并给出正确性和安全性证明,但此协议计算效率低.文献[13]所提协议不仅可以判定点与任意多边形的包含问题而且比现有协议更加高效和安全.文献[2,8-11]研究的都是点包含问题,但在实际应用中具有局限性.文献[14]研究了点与曲线关系的隐私保护协议,解决了在不泄露任何信息的情况下和在不同情形下判定点与曲线位置关系的问题.文献[15] 基于保密点积协议,研究了空间线与面的夹角问题和两线间的距离问题,有效降低了计算复杂性.文献[16]基于拉格朗日乘数法,研究了几何图形的相交问题并给出此类问题的解决方案.文献[17]根据几何方法提出了保护私有信息的直线与椭圆和直线与双曲线位置关系判定协议,但所提协议只能单一地判定直线与椭圆或者直线与双曲线的位置关系.
本文针对直线与椭圆、双曲线和抛物线的位置关系判定问题提出了直线与二次曲线位置关系的安全判定协议.首先,需要利用Paillier同态加密算法,保密点积协议通过构造辅助数据来分别隐藏自己的具体数据;然后,利用社会主义百万富翁协议通过比较辅助数据的大小来判断函数值;最后,根据相关函数值安全判定直线与二次曲线的具体位置关系,并对该协议的正确性和安全性分别进行证明.
2 预备知识
2.1 基础协议
百万富翁协议由姚期智教授[1]于1982年首次提出,问题:有两个百万富翁,他们想知道对方是否比自己更富有,但又不想让对方知道自己的财富值,所以需要保密地进行比较.具体原理如下:
输入:Alice拥有保密数据i,Bob拥有保密数据j.
输出:Alice和Bob安全地计算函数GT,GT(i,j)=[i>j](GT(i,j)).当GT(i,j)=1(GT(i,j)=1)时,i>j成立;否则GT(i,j)=0(GT(i,j)=0),i≤j.
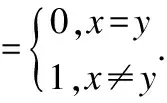
输入:Alice拥有保密数a,Bob拥有保密数b.
输出:P(a,b)
1)Alice计算EK1(a),Bob计算EK2(b).
2)Alice和Bob交换EK1(a),EK2(b).
3)Alice计算EK1(EK2(b)),Bob计算EK2(EK1(a)).
4)Alice和Bob交换EK1(EK2(b)),EK2(EK1(a)),若EK1(EK2(b))=EK2(EK1(a)),输出0;否则,输出1.
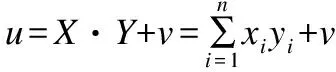
2.2 Paillier加密方案
Paillier加密方案[19]由密钥生成、加密算法和解密算法三部分组成:
密钥产生:
随机的选取两个素数p和q,且满足gcd(pq,(p-1)(q-1))=1.计算n=pq和λ=lcm(p-1,q-1).
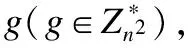
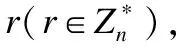
解密:m=L(cλmodn2)umodn.
本文运用的是Paillier加密方案的加法同态性质Ek(x)·Ek(y)=Ek(x+y),由加法同态性的性质可以推算出E(x)m=E(mx).
2.3 安全性证明
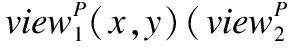
定义1.(半诚实参与者的保密性[20]) 对于一个函数F,如果存在概率多项式时间算法S1与S2(也称这样的多项式时间算法为模拟器)使得
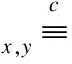
(1)
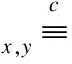
(2)

3 直线与二次曲线位置关系的解决方案
3.1 问题描述
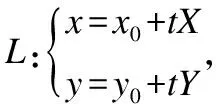

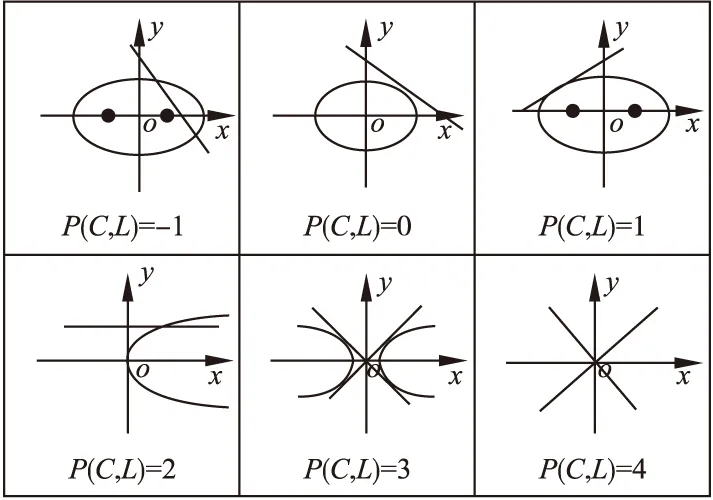
图1 直线与二次曲线的位置关系Fig.1 Line and quadratic curve position relationship
3.2 主要思想
文献[17]解决了直线与椭圆、双曲线的位置判定问题,但具有特殊性.本文提出了一种安全高效的方案,并具有可扩展性.方案的主要思想是把直线方程代入到二次曲线方程,整理得关于t的方程:
(a11X2+a12XY+a22Y2)t2+[(2a11x0+a12y0+a13)X+
(a12x0+2a22y0+a23)Y]t+
即
φ(X,Y)t2+[XF1(x0,y0)+YF2(x0,y0)]t+F(x0,y0)=0
(1)
1)当φ(X,Y)≠0时,方程(1)是关于t的二次方程,其判别式为:
Δ=[XF1(x0,y0)+YF2(x0,y0)]2-4φ(X,Y)F(x0,y0)
①Δ>0时,方程(1)有两个不等的实根t1,t2,直线与曲线相交,即P(C,L)=-1.
②Δ<0时,方程(1)无解,直线与曲线相离,即P(C,L)=0.
③Δ=0时,方程(1)有两个相等的实根t1,t2,直线与曲线相切,即P(C,L)=1.
2)当φ(X,Y)=0时,方程(1)为:
[XF1(x0,y0)+YF2(x0,y0)]t+F(x0,y0)=0
(2)
①当XF1(x0,y0)+YF2(x0,y0)≠0时,方程(2)有唯一解,直线与曲线有唯一实交点,即P(C,L)=2.
②当XF1(x0,y0)+YF2(x0,y0)=0,F(x0,y0)≠0时,方程(2)无解,直线与曲线没有交点,即P(C,L)=3.
③当XF1(x0,y0)+YF2(x0,y0)=0,F(x0,y0)=0时,方程(2)有无穷多解,直线与曲线有无数个交点(此时二次曲线为退化的两相交直线,直线L必为其中的一条),即P(C,L)=4.
要安全判定直线与二次曲线的位置关系:
1)利用Paillier同态加密算法将自己二次曲线方程的系数隐藏,并构造辅助数据M1,N1(M1=φ(X,Y)+N1,N1是Bob在协议3步骤1中所选随机数的总和),通过社会主义百万富翁协议比较M1是否等于N1来判断函数φ(X,Y)是否等于0.若φ(X,Y)≠0,则判断判别式Δ的大小;若φ(X,Y)=0,则判断函数XF1(x0,y0)+YF2(x0,y0)的值.
2)利用Paillier同态加密算法和百万富翁协议来安全判断判别式Δ与0的大小关系.
3)利用保密点积协议将双方生成的私有向量进行乘积,并构造辅助数据UA,UB(UA=XF1(x0,y0)+YF2(x0,y0)+UB,其中UB是Bob选择的随机数.)来隐藏自己的具体数据,通过社会主义百万富翁协议比较的UA,UB大小关系来判断函数XF1(x0,y0)+YF2(x0,y0)是否等于0,若函数XF1(x0,y0)+YF2(x0,y0)=0,则判断函数F(x0,y0)的值.
4)利用Paillier同态加密算法和社会主义百万富翁协议来安全判断函数F(x0,y0)是否等于0.
5)根据相关函数值及方案的主要思想安全判定直线与二次曲线的具体位置关系.
3.3 协议设计
协议:直线与二次曲线位置关系的安全判定协议(记为协议P0)
输出:P(C,L)
协议3的执行过程:
步骤1.
①设Paillier同态加密方案是(G,E,D),安全参数是k,Alice运行G(k)生成同态加密的公钥和私钥,Alice将生成的公钥发送给Bob.
②Alice用公钥将E(C)={E(a11),E(a12),E(a22)}加密,并发送给Bob.
③Bob选取随机数R1,R2,R3,并计算.
T1=E(a11)X2·E(R1)=E(a11X2+R1)
T2=E(a12)XY·E(R2)=E(a12XY+R2)
T3=E(a22)Y2·E(R3)=E(a22Y2+R3)
N1=R1+R2+R3
并发送给Alice.
⑤Alice与Bob通过社会主义百万富翁协议比较M1是否等于N1.若M1≠N1,则φ(X,Y)≠0,执行步骤2;若M1=N1,则φ(X,Y)=0,执行步骤3.
步骤2.
①Alice计算
I9=4a13a22-2a12a23,I10=2a13a23-4a12a33
对Ii(i=1,2,…,10)用公钥进行加密,并将E(Ii)发送给Bob.
②Bob选取随机数R4,R5,R6,R7,R8,R9,R10,R11,R12,R13,并计算
T5=E(2a12a13-4a11a23)X2y0·E(R5)=E[(2a12a13-4a11a23)X2y0+R5]
T8=E(2a12a23-4a13a22)Y2x0·E(R8)=E[(2a12a23-4a13a22)Y2x0+R8]
T11=E(4a11a23-2a12a13)XYx0·E(R11)=E[(4a11a23-2a12a13)XYx0+R11]
T12=E(4a13a22-2a12a23)XYy0·E(R12)=E[(4a13a22-2a12a23)XYy0+R12]
T13=E(2a13a23-4a12a33)XY·E(R12)=E[(2a13a23-4a12a33)XY+R13]
并发送给Alice.
④Alice与Bob通过百万富翁协议比较M2,N2的大小,若M2>N2,则Δ>0,输出P(C,L)=-1;若M2 步骤3. ③Alice与Bob利用社会主义百万富翁协议比较UA与UB的大小,若UA≠UB,则XF1(x0,y0)+YF2(x0,y0)≠0,输出P(C,L)=2;若UA=UB,则XF1(x0,y0)+YF2(x0,y0)=0,执行步骤4. 步骤4. ①Alice用公钥加密E(C)={E(a11),E(2a12), E(a22),E(2a13),E(2a23),E(a33)}并发送给Bob. ②Bob选取随机数r1,r2,r3,r4,r5,r6,并计算 t2=E(a12)x0y0·E(r2)=E(a12x0y0+r2) t4=E(a13)x0·E(r4)=E(a13x0+r4) t5=E(a23)y0·E(r5)=E(a23y0+r5) t6=E(a33)·E(r6)=E(a33+r6) 并发送给Alice. ④Alice与Bob协同调用社会主义百万富翁协议比较M3是否等于N3.若M3≠N3,则F(x0,y0)≠0,输出P(C,L)=3;若M3=N3,则F(x0,y0)=0,输出P(C,L)=4. 定理1.协议P0是正确的. 证明: 2)当M2>N2时,由步骤2中的①②③可知:[XF1(x0,y0)+YF2(x0,y0)]2>4φ(X,Y)·F(x0,y0);根据前面3.2可知Δ>0. 3)由1)2)可知,当M1≠N1且M2>N2时,即φ(X,Y)≠0且Δ>0时,根据前面3.2可知直线L与曲线C有两个不同的实交点,故协议P0是正确的.同理可证其它5种情况. 定理2.协议P0是安全的. 证明通过构造出使(1)和(2)成立的模拟器S1和S2来证明其安全性. 1)构造模拟器S1. 在本方案中 S1的模拟过程如下: 因为 令 2)构造模拟器S2. 在本方案中 S2的模拟过程如下: 因为 令 根据预备知识2.6的安全性证明可知协议P0是安全的. 计算复杂性:文献[17]协议二共调用一次点线关系判定协议和一次点积协议.文献[17]协议三共调用三次点积协议.本文协议P0共执行19次Pailler加密运算,19次Pailler解密运算和一次点积协议.假设安全参数为m,一次点积协议至少需要2mlgk次模指数运算;一次点线关系判定协议共需要3次Pailler加密运算、3次Pailler解密运算;Pailler一次加密需要2次模指数运算,一次解密需要1次模指数运算.一般情况下当m>5,k>8时才能达到基本的安全级别,文献[17]协议二共需2mlgk+3×2+3次模指数运算,故至少需要39次模指数运算;协议三共需6mlgk次模指数运算,故至少需要90次模指数运算;本文协议P0共需2mlgk+19×2+19次模指数运算,故至少需要87次模指数运算. 通信复杂性:在安全多方计算研究中通常用通信轮数来衡量通信复杂性,文献[17]协议二通信轮数为m+3次,协议三通信轮数为3m次,本文协议P0通信轮数为m+7次.各方案复杂性比较如下页表1所示,功能性比较如下页表2所示. 表1 各方案复杂性比较 协 议计算复杂性通信复杂性文献[17]协议22mlgk+9m+3文献[17]协议36mlgk3m本文协议P02mlgk+57m+7 贡献总结:本文利用判别式法提出直线与二次曲线位置关系的安全判定协议,该协议首先通过Paillier同态加密算法和百万富翁协议判断函数φ(X,Y)是否等于0.①若φ(X,Y)≠0,则利用Paillier同态加密算法和百万富翁协议判断判别式Δ的大小.若Δ>0,输出P(C,L)=-1,直线与曲线相交; 表2 各方案功能性比较 方 法判定直线与椭圆关系判定直线与双曲线关系判定直线与抛物线关系文献[17]协议2能不能不能文献[17]协议3不能能不能本文协议P0能能能 若Δ<0,输出P(C,L)=0,直线与曲线相离;若Δ=0,输出P(C,L)=1,直线与曲线相切.②若φ(X,Y)=0,则利用保密点积协议和社会主义百万富翁协议判断函数XF1(x0,y0)+YF2(x0,y0)是否等于0.若函数XF1(x0,y0)+YF2(x0,y0)≠0,输出P(C,L)=2,直线与曲线有唯一实交点;若函数XF1(x0,y0)+YF2(x0,y0)=0,则利用Paillier同态加密算法和社会主义百万富翁协议判断函数F(x0,y0)的值是否等于0.若函数F(x0,y0)≠0,输出P(C,L)=3,直线与曲线没有交点;若函数F(x0,y0)=0,输出P(C,L)=4,直线与曲线有无数个交点(此时二次曲线为退化的两相交直线,直线L必为其中的一条). 方案比较:本文协议P0在计算复杂性和通信复杂性上比文献[17]协议二略高,但在功能上具有明显优势.文献[17]协议二只能判断直线与椭圆的位置关系,而协议P0不仅可以判断直线与椭圆的位置关系而且可以判定直线与双曲线和抛物线的位置关系.此外,协议P0不仅在计算复杂性和通信复杂性上比文献[17]协议三的解决方案降低了3倍,而且在功能上也有很大改善.文献[17]协议三只能判断直线与双曲线的位置关系,而协议P0既可以判定直线与双曲线的位置关系也可以判定直线与椭圆和抛物线的位置关系.总之,协议P0计算效率和通信效率更高,应用范围更广. 在半诚实模型下,本文将保密点积协议和Paillier同态加密方案的巧妙结合提出了判定直线与二次曲线位置关系的解决方案,安全判定了两者之间的位置关系,并且对协议P0的正确性和安全性分别给出证明.因为协议P0是基于半诚实模型的,还有不足之处,在恶意模型下对直线与二次曲线位置关系的保密判定协议进行研究和分析会比较困难,未来我们将继续对此进行探讨. [1] Yao A C.Protocols for secure computations[C].Proceedings of the 23rd Annual IEEE Symposium on Foundations of Computer Science(FOCS 1982),Chicago,USA,Nov 3-5,1982,Los Alamitors,CA:IEEE Computer Society,1982:160-164. [2] Atallah M J,Du W L.Secure multi-party computational geometry[C].Lecture Notes in Computer Science 2125(LNCS 2001),RI,USA,Aug 8-10,2001,Berlin:Springer,2001:165-179. [3] Du W L,Atallah M J.Secure multi-party computation problems and their applications:a review and open problems[C].Proceedings of the New Security Paradigms Workshop 2001(NSPW2001),Cloudcroft,New Mexico,USA,September 10-13,2001,Berlin:Springer,2001:11-20. [4] Du W L,Atallah M J.Privacy-preserving cooperative scientific computations[C].IEEE Workshop on Computer Security Foundations,Washington(CSFW 2001),DC,USA,June 11-13,2001,Los Alamitors,CA:IEEE Computer Society,2001:273-282. [5] Luo Yong-long,Huang Liu-sheng,Jing Wei-wei,et al.Privacy-preserving cross product protocol and its applications[J].Chinese Journal of Computers(CJE),2007,30(2):248-254. [6] Sun Mao-hua,Luo Shou-shan,Xin Yang,et al.Secure two-party line segments intersection scheme and ItsApplication in privacy-preserving convex hull intersection[J].Journal on Communications(JCM),2013,34(1):30-42. [7] Li Shun-dong,Dai Yi-qi,Wang Dao-shun,et al.Secure multi-party computations of geometric intersections[J].Journal of Tsinghua University(Science and Technology)(JTU),2007,47(10):1692-1695. [8] Li Shun-dong,Dai Yi-qi.Secure Two-party computational geometry[J].Journal of Computer and Technology(JCT),2005,20(2):258-263. [9] Luo Yong-long,Huang Liu-sheng,Zhong Hong.Secure Two-party point-circle inclusion problem[J].Journal of Computer and Technology(JCT),2007,22(1):88-91. [10] Luo Yong-long,Huang Liu-sheng.A secure protocol for determining whether a point is insider a convex polygon[J].Chinese Journal of Electronics(CJE),2006,15(4):578-582. [11] Zhang Jing,Luo Shou-shan,Yang Yi-xian,et al.Research on theprivacy-preserving point-in-polygon protocol[J].Journal on Communications(JCM),2016,37(4):87-95. [12] Chen L,Lin B.Privacy-preserving point-inclusion two-party computation protocol[C].2013 International Conference on Computational and Information Sciences(CAIS 2013),Shiyang,China,June 21-23,2013,Los Alamitors,CA:IEEE Computer Society,2013:257-260. [13] Daoshurr W.Efficient secure multiparty computational geometry[J].Chinese Journal of Electronics(CJE),2010,19(2):324-328. [14] Liu L,Wu C,Li S.TWO privacy-preserving protocols for point-curve relation[J].Journal of Electronics(CJE),2012,29(5):422-430. [15] Zhong Hong,Sun Yan-fei,Yan Fei-fei,et al.Privacy-preserving relative position calculation protocols for spatial geometric objects [J].Journal of Harbin Engineering University(JHEU),2011,32(4):458-463. [16] Qin J,Duan H,Zhao H,et al.A new lagrange solution to the privacy-preserving general geometric intersection problem[J].Journal of Network and Computer Applications(JNCA),2014,46(C):94-99. [17] Zhang Di.Privately determining protocol of line and ellipseor hyperbola position relationship[D].Kunming:Yunnan University,2015. [18] Zhang X H,Miao Y Q,Jie S U,et al.Privacy preserving association rules mining in vertically partitioned data[J].Computer Engineering &Design(CED),2012,33(5):1867-1870. [19] Jie Hong W U,Zhang P,Shi X B.Research of MA protection based on addition-multiplication homomorphism and composite function technology[J].Journal of Chinese Computer Systems(JCCS),2012,33(10):2223-2226. [20] Reimer B,Fried R,Mehler B,et al.Brief report:examining driving behavior in young adults with high functioning autism spectrum disorders:a pilot study using a driving simulation paradigm[J].Journal of Autism & Developmental Disorders(JADD),2013,43(9):2211-2217. 附中文参考文献: [6] 孙茂华,罗守山,辛 阳.安全两方线段求交协议及其在保护隐私凸包交集中的应用[J].通信学报,2013,34(1):30-42. [11] 张 静,罗守山,杨义先,等.保护私有信息的点包含协议研究[J].通信学报,2016,37(4):87-95. [15] 仲 红,孙彦飞,燕飞飞,等.保护私有信息几何对象的相对位置计算[J].哈尔滨工程大学学报,2011,32(4):458-463. [17] 张 迪.直线与椭圆、直线与双曲线位置关系的安全判定协议[D].昆明:云南大学,2015.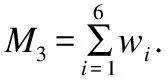
4 协议正确性与安全性证明
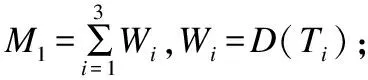
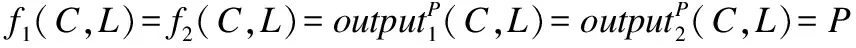
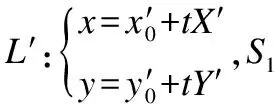
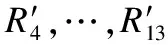
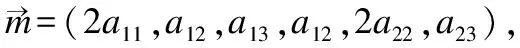

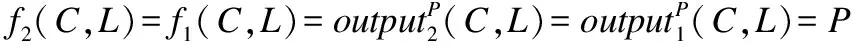
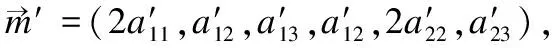

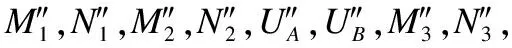
5 性能分析
Table 1 Complexity comparing of schemes
Table 2 Function comparing of schemes
6 结束语

