轻量级可调分组密码QARMA的不可能差分攻击

张国强,张文英

(山东师范大学 信息科学与工程学院,济南 250014)

1 引 言

分组密码作为对称加密的一个重要分支,在信息安全方面具有极其重要的作用,一直是研究的热点.分组密码的设计一直遵循香农提出的“混淆”与“扩散”原则.

可调分组密码是由Moses Lisko等人在2002年提出的.可调分组密码是一种带有额外输入的分组密码,我们通常称这一额外输入为调柄(tweak).调柄并不需要保密,通过加入它来提高加密的灵活性.

近些年,随着微型设备如RIFD、无线传感等技术的飞速发展,轻量级分组密码应运而生并成为研究的热点.许多轻量级分组密码被提出来,如LBlock[1]、Khudra[2]、RECTANGLE[3]、Lilliput[4]、SIMON[5]等.另外,我国的王鹏博士、吴文玲教授等基于CTR模式利用Hash-CTR-Hash结构设计了HCTR模式[6].

由Roberto Avanzi设计的QARMA算法是一种轻量级可调分组密码[7].在2016年,QARMA被引进到ARMv8-A架构,用来实现软件保护.QARMA算法有64比特和128比特两个版本.

不可能差分攻击是差分密码分析的一个变种,是由Kundesn[8]和Biham[9]分别独立提出的.不可能差分密码分析方法是利用概率为0的特征,其基本思想是排除那些使得概率为0的特征或者差分的候选密钥.对于概率为0的差分路径,如果我们用正确的密钥解密密文对时,一定不会得到符合该路径的差分;而当我们用猜测的密钥去解密密文时,如果得到了符合该路径的差分,则我们猜测的密钥是错误的,应该筛去.当我们筛掉全部的错误密钥后,剩下的就是我们要恢复的正确密钥.

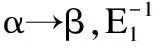
由于该分析方法简单有效,因此在算法分析中得到广泛应用,成功的用于分析大量的分组密码,如:PRINCE[10],SIMECK[11],LBlock-s[12],AES[13],MIBS[14]等.

到目前为止,还没有任何用不可能差分攻击对QARMA算法进行分析的文档.据我们所知,对于QARMA算法最好的攻击是文献[15]中的中间相遇攻击.该攻击在包含了反仿射结构的5轮区分器的基础上,对10轮的QARMA-64算法进行了攻击,攻击所需的时间复杂度为270.1次10轮加密,存储复杂度为2116个192比特序列,数据复杂度为253个明文.

本文使用不可能差分攻击对QARMA算法进行分析.我们给出了5轮的不可能差分区分器,进而对10轮的QARMA算法进行了攻击.另外,通过使用两条不同的差分路径,来进一步降低了攻击的时间复杂度.与现有的中间相遇攻击相比[15],我们的攻击的时间复杂度和存储复杂度均有所降低.据我们所知,这是首次使用不可能差分对该算法进行分析.

2 QARMA算法

在本节中首先对本文中用到的符号进行说明,然后对QARMA算法进行简要的介绍.

2.1 符号说明

P:明文

C:密文

ω0:主密钥的左半部分

K0:主密钥的右半部分

T:调柄

Ci:轮常数

Xi,Yi,Zi,Wi:加密过程中第i轮的状态

Ki[j]:第i轮的密钥的第j个半字节

‖:级联操作

>>>:循环右移

2.2 QARMA算法介绍

QARMA是带有调柄(tweak)的可调分组密码.QARMA算法加密过程由三部分组成(如图1所示),其中第一部分和第三部分是完全相反的操作变换.QARMA的具体加密流程如图2所示.

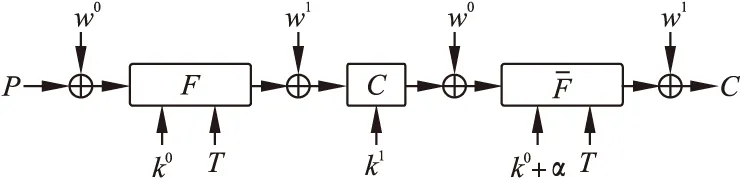
图1 QARMA整体结构Fig.1 Overall scheme

QARMA算法的分组长度有64比特和128比特两个版本.接下来,我们以64比特版本为例来对加密过程中的操作进行具体说明.

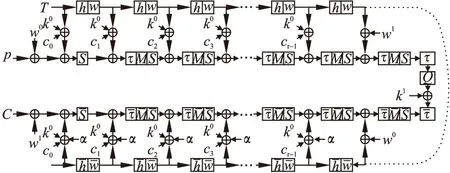
图2 QARMA具体结构Fig.2 Structure of QARMA

主密钥长度是128比特,分为等长的两部分(ω0‖K0),各为64比特.加密过程中还用到密钥ω1‖K1,其中

ω1=o(ω0)=(ω0>>>1)+(ω0>>(63)),K1= K0.

QARMA-64是带有仿反射结构的SPN结构的分组密码.加密过程可以看做是对64比特内部状态的一系列操作.内部状态表示成一个4×4的方阵,方阵中每个元素是4比特(n=64),如下所示:

加密过程中的第一部分包含如下四个基本操作:

密钥加操作(AK):将内部状态与轮密钥Ki、调柄T以及轮常数Ci进行模2加操作.

位置变换操作(τ):将内部状态的16个元素进行位置变换:

τ=[0,11,6,13,10,1,12,7,5,14,3,8,15,4,9,2]

列混合操作(M):用状态矩阵M乘以内部状态的每一列.矩阵M如下所示:

值得注意的是,矩阵M是对合矩阵(M2=I).一个元素乘以ρi相当于将这个元素向左循环移动i比特.

字节替换操作(S):内部状态的每个元素进一个4比特的s盒.

表1 QARMA-64 s盒
Table 1 Sbox of QARMA-64

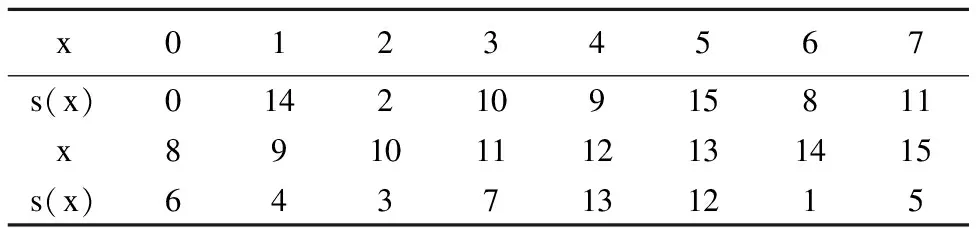
x01234567s(x)014210915811x89101112131415s(x)6437131215

加密流程的第三部分是与第一部分完全相反的操作.在第一轮和最后一轮省略掉了位置变换和列混合操作,只进行密钥加和进s盒操作.

加密流程的第二部分包含前向一轮、后向一轮以及一个仿反射结构.仿反射结构包含四个操作:位置变换、列混合、密钥加、位置变换逆变换.在列混合操作中用到的矩阵Q和M是一样的.

3 QARMA的10轮不可能差分攻击

在本节中,我们首先给出了一个关于QARMA的列混合变换的性质,然后给出了一个5轮的不可能差分区分器,最后在5轮不可能差分区分器的基础上,对10轮的QARMA进行攻击.

3.1 QARMA列混合变换的性质

性质1.如果一列中有一个位置差分为0,另外三个元素存在差分,那么经过列混合变换后在原来差分为0的位置有差分,其余三个位置没有差分的概率为2-8.例如:P((0***)→(*000))=2-8(其中0表示差分为0,*表示差分不为0,两者都代表一个4比特的元素).

证明:

在这里我们用一个一般性的例子((0***)→(*000))进行说明.我们用x1x2x3x4表示输入状态一列中的4个位置的差分.首先假设输入只有第一个位置上差分为0(x1=0,x2≠0,x3≠0,x4≠0),输出的第一个位置差分不为0,第二、三个位置上差分为0,不考虑第四个位置的差分,那么能得到这种输出的概率为2-8,即:P((0***)→(*00?))=2-8.根据以上条件,我们可以列出以下等式:

进而可以得到:ρ·x1+ρ·x3+ρ2·x4=0,ρ2·x1+ρ·x2+ρ·x4=0.由此可以计算y=ρ·x1+ρ2·x2+ρ·x3=0.所以输出三个位置没有差分的概率为2-8.

当我们改变输入或者输出差分为0的位置时,使用同样的方法可以得到此结论.因此性质1得证.

3.2 5轮不可能差分区分器

如图3所示(白色位置表示差分为0,黑色位置表示一定存在差分,阴影位置表示差分不确定),当输入为差分为(a000 0a00 0000 0000)时,经过两轮的第一部分变换以及仿反射结构后,输出差分为(**?* 0*?* *?** *?*0).当输出差分为(0000 *000 0000 0000)时,解密三轮,我们得到输出差分为(*??* **?? ???? ?*?*).我们发现在第4和第15个元素位置存在矛盾.由此我们得到了一条5轮的不可能差分路径:(a000 0a00 0000 0000)→(0000 *000 0000 0000)(其中,a表示差分为a,*表示一定存在差分,？表示差分不确定).

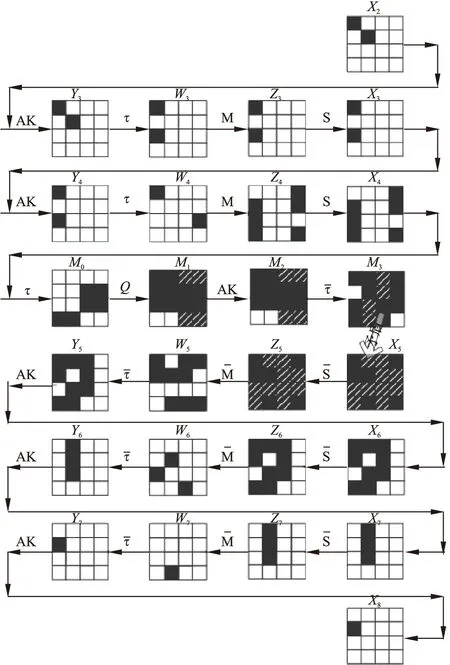
图3 QARMA 5轮不可能差分区分器Fig.3 Distinguisher of 5-Round on QARMA

3.3 10轮不可能差分攻击

利用上述的不可能差分路径,我们在前面加两轮,后面加三轮,对10轮的QARMA进行攻击.

选取2n个明文结构,每个结构里面的明文在(4,5,10,11,14,15)6个位置上取遍所有值,其余10个位置上固定.每个结构中包含224个明文,可以构成224×(224-1)/2≈247个明文对.2n个结构可以得到2n+47个明文对.

1)对于每个结构,将明文加密得到密文,看密文在C[0,1,2,3,6,9,12]位置的差分是否为0,差分不为0的删除.经过这一步后,剩余的明密文对数量为2n+47×2-28=2n+19.

2)猜测密钥k1[4,11,14],根据密钥编排,可以求出k2[4,11,14].对于剩下的每一对,可以求出Y2[4,11,14],经过位置变换操作后,可以求出W2[1,9,13].进而可以计算ΔZ2[1,5,9,13],如果ΔZ2[1,9,13]=0,则保留;否则,删除.根据性质1,经过这一步后剩余的明密文对的数量为2n+19×2-8=2n+11.

图4 QARMA 10轮不可能攻击Fig.4 Impossible differential attack on QARMA

3)根据密钥编排及k1[4,11,14],可以计算k10[4,11,14]和k9[4,11,14].对于剩下的每一对,可以求出Y9[4,11,14],经过位置变换操作后,可以求出W9[1,9,13].进而可以计算ΔZ9[1,9,13],如果ΔZ9[1,9,13]=0,则保留;否则,删除.经过这一步后剩余的明密文对的数量为2n+11×2-8=2n+3.

4)猜测密钥k1[5,10,15],根据密钥编排,可以求出k2[5,10,15].对于剩下的每一对,可以求出Y2[5,10,15],经过位置变换操作后,可以求出W2[4,8,12].进而可以计算ΔZ2[0,4,8,12],如果ΔZ2[4,8,12]=0且ΔZ2[0]=ΔZ2[5],则保留;否则,删除.经过这一步后剩余的明密文对的数量为2n+3×2-12=2n-9.

5)根据密钥编排及k1[5,10,15],可以计算k10[5,10,15]和k9[5,10,15],可以求出Y9[5,10,15],经过位置变换操作后,可以求出W9[4,8,12].进而可以计算ΔZ9[4,8,12],如果ΔZ9[4,8,12]=0,则保留;否则,删除.经过这一步后剩余的明密文对的数量为2n-9×2-8=2n-17.

6)猜测k10[7,8,13],可以计算出k9[7,8,13],可以求出Y9[7,8,13],经过位置变换操作后,可以求出W9[3,7,11].进而可以计算ΔZ9[3,7,11],如果ΔZ9[3,7,11]=0,则保留;否则,删除.经过这一步后剩余的明密文对的数量为2n-17×2-8=2n-25.

7)根据k10[5,15],推导出k8[5,15].猜测k8[0],可以计算出Y8[0,5,15],进而计算W8[0,8,12],进一步计算ΔZ8[0,8,12].根据性质1,ΔZ8[0,8,12]=0的概率为2-8.

表2 时间复杂度和空间复杂度
Table 2 Time complexity and memory complexity

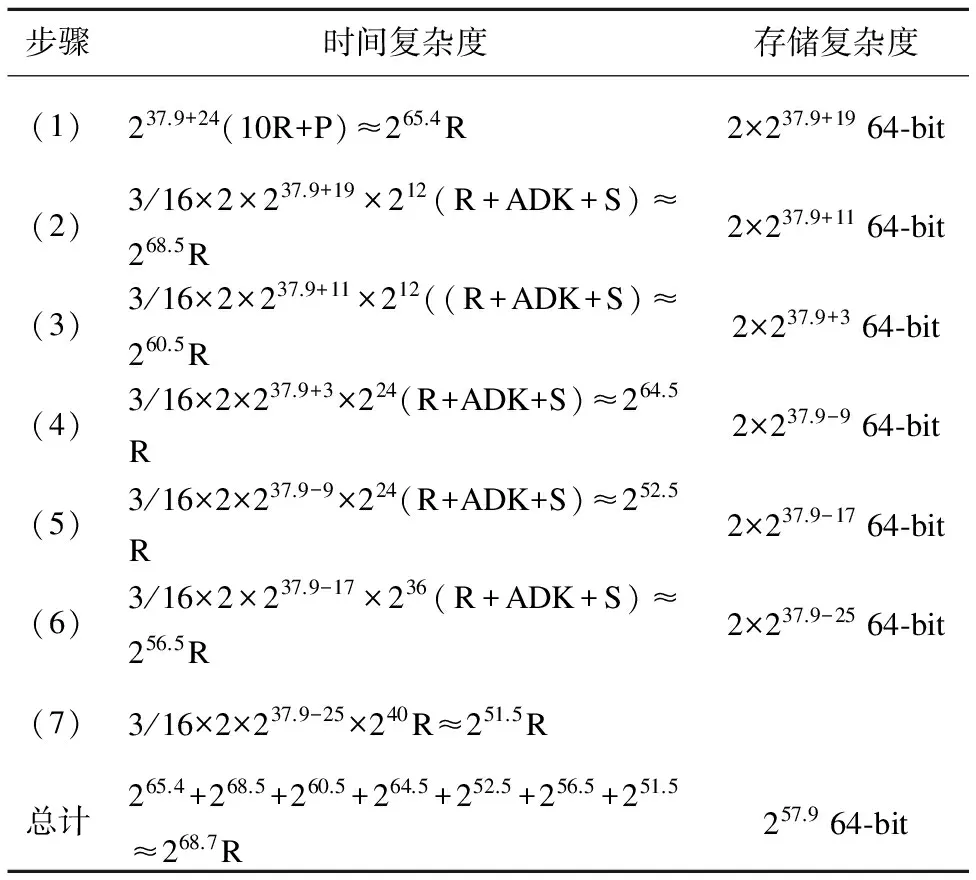
步骤时间复杂度存储复杂度(1)237．9+24(10R+P)≈265．4R2×237．9+1964⁃bit(2)3/16×2×237．9+19×212(R+ADK+S)≈268．5R2×237．9+1164⁃bit(3)3/16×2×237．9+11×212((R+ADK+S)≈260．5R2×237．9+364⁃bit(4)3/16×2×237．9+3×224(R+ADK+S)≈264．5R2×237．9-964⁃bit(5)3/16×2×237．9-9×224(R+ADK+S)≈252．5R2×237．9-1764⁃bit(6)3/16×2×237．9-17×236(R+ADK+S)≈256．5R2×237．9-2564⁃bit(7)3/16×2×237．9-25×240R≈251．5R总计265．4+268．5+260．5+264．5+252．5+256．5+251．5≈268．7R257．964⁃bit

我们总共猜测了40比特的密钥,经过上述一系列操作后,剩余的错误密钥数量为N=(240-1)×(1-2-8)2^(n-25).为了使N<1,我们取n=37.9.这样,我们就可以得到唯一正确的40比特密钥k0[0,4,5,7,8,10,11,13,14,15].

3.4 复杂度分析

我们选择了237.9个明文结构,所以数据复杂度为237.9+24=261.9个明文.表2显示了每一步的时间复杂度和存储复杂度.所以时间复杂度是268.7轮加密,相当于265.2次10轮加密,存储复杂度为257.9个64比特序列.

通过穷举来恢复剩余的88比特密钥,恢复这剩余的88比特密钥所需的时间复杂度为288(10R+P)≈291.3R.所以总的时间复杂度为270.1R +291.3R≈291.3R.可以发现,总的时间复杂度主要是由穷举剩余的88比特密钥所造成的.

4 双区分器密钥恢复算法

在本节,使用新的方法来减少恢复剩余的88比特密钥的时间复杂度.在恢复了40比特密钥的基础上,先恢复k0剩余的24比特,对剩余的ω0的64比特通过穷举来恢复.

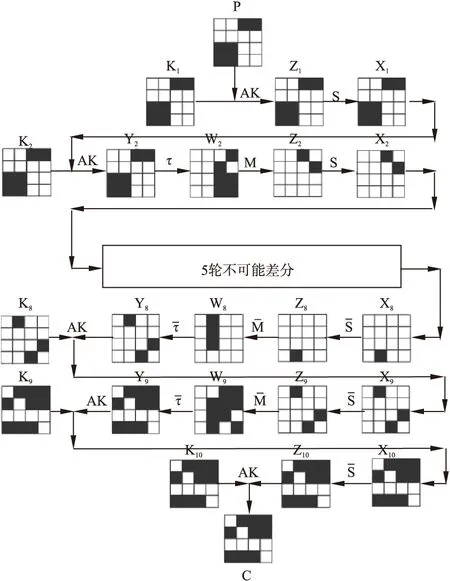
图5 不同的不可能差分攻击Fig.5 Another impossible differential acttack

我们使用新的5轮不可能差分路径(00a0 000a 0000 0000)→(0000 0000 0000 0*00)(构造方法与上一个不可能差分区分器类似).在上述区分器前面加两轮,后面加上三轮,构成10轮的不可能差分攻击(如图5所示).

在恢复48比特密钥时,使用了237.9个明文结构,总共是261.9个明文.可以使得选择的明文前15个元素取遍所有的可能,最后一个元素取21.9个可能.同样可以使用这些明文来构成237.9个新的明文结构,每个结构里面的明文在(2,3,8,9,12,13)6个位置上取遍所有值,其余10个位置上固定.每个结构中包含224个明文,可以构成224×(224-1)/2≈247个明文对.2m个结构可以得到2m+47个明文对.

8)对于每个结构,将明文加密得到密文,看密文在C[0,5,8,9,10,11,15]位置的差分是否为0,差分不为0的删除.经过这一步后,剩余的密文对数量为2m+47×2-28=2m+19.

9)由于已经确定了k1[8,13] 和k2[8,13],猜测k1[2],推出k2[2].对于剩余的每一对,可以部分解密求得W2[3,11,15].进而可以计算ΔZ9[3,7,11,15],如果ΔZ9[3,11,15]=0,则保留;否则,删除.经过这一步后剩余的密文对的数量为2m+19×2-8=2m+11.

10)根据密钥编排以及k1[2,7,13],可以推出k10[2,7,13] 和k9[2,7,13],从而可以部分解密得到W9[3,7,15],进而可以计算ΔZ9[3,7,15],如果ΔZ9[3,7,15]=0,则保留;否则,删除.经过这一步后剩余的明密文对的数量为2m+11×2-8=2m+3.

11)猜测k1[3,9,12],可以推出k2[3,9,12],可以部分解密得到W2[6,10,14],进而可以计算ΔZ2[2,6,10,14],如果ΔZ2[6,10,14]=0且ΔZ2[2]=ΔZ2[7],则保留;否则,删除.经过这一步后剩余的密文对的数量为2m+3×2-12=2m-9.

12)根据密钥编排以及k1[3,12],可以推出k10[3,12]和k9[3,12].猜测k10[6],可以推出k9[6],从而可以部分解密得到W9[2,6,10],进而可以计算ΔZ9[2,6,10],如果ΔZ9[2,6,10]=0,则保留;否则,删除.经过这一步后剩余的密文对的数量为2m-9×2-8=2m-17.

13)猜测k10[1],推出k9[1].由于k10[4,14]和k9[4,14]已经确定,对于剩余的对,经过部分加密,可以求得W9[5,9,13],进而求得ΔZ9[5,9,13].如果ΔZ9[5,9,13]=0,则保留;否则,删除.经过这一步后剩余的密文对的数量为2m-17×2-8=2m-25.

14)根据k10[1,11,14],推导出k8[1,11,14].进而可以计算W8[1,5,9],进一步计算ΔZ8[1,5,9].根据性质1,ΔZ8[1,5,9]=0的概率为2-8.

我们总共猜测了24比特的密钥,经过上述一系列操作后,剩余的错误密钥数量为N=(224-1)×(1-2-8)2^(m-25).为了使N<1,取m=37.1.这样,就可以得到唯一正确的24比特密钥.

恢复剩下的64比特密钥所需的时间复杂度为264(10R+P)≈267.5R.

表3 时间复杂度和空间复杂度
Table 3 Time complexity and memory complexity

步骤时间复杂度存储复杂度8)2×237．1+1964⁃bit9)3/16×2×237．1+19×24(R+ADK+S)≈259．7R2×237．1+1164⁃bit10)3/16×2×237．1+11×24(R+ADK+S)≈251．7R2×237．1+364⁃bit11)3/16×2×2237．1+3×216(R+ADK+S)≈255．7R2×237．1-964⁃bit12)3/16×2×2237．1-9×220(R+ADK+S)≈247．7R2×237．1-1764⁃bit13)3/16×2×2237．1-17×224(R+ADK+S)≈243．7R2×237．1-2564⁃bit14)3/16×2×2237．1-25×224R≈235．7R总计259．7+251．7+255．7+247．7+243．7+235．7≈259．8R257．164⁃bit

因此,数据复杂度为261.9个明文,总的时间复杂度为268.7+259.8+267.5≈269.3轮加密,相当于265.8次10轮加密,存储复杂度为257.9+257.1≈258.6个64比特序列.

5 总 结

本文通过使用5轮的不可能差分路径对10轮的QARMA-64进行攻击.据我们所知,这是首次使用不可能差分攻击对QARMA-64进行分析.此外我们通过使用两个不同的5轮不可能差分区分器来降低恢复密钥的时间复杂度.文献[15]中的中间相遇攻击的时间复杂度为270.1次10轮加密,存储复杂度为2116个192比特序列,而我们的时间复杂度为265.8次10轮加密,空间复杂度为258.6个64比特序列,在时间复杂度和存储复杂度方面我们的攻击存在明显的优势.

[1] Wu Wen-ling,Zhang Lei.LBlock:a lightweight block cipher [C].Applied Cryptography and Network Security (ACNS2011),LNCS 6715,2011:327-344.

[2] Souvik Kolay,Debdeep Mukhopadhyay.Khudra:a new lightweight block cipher for FPGAs[C].International Conference on Security,Privacy,and Applied Cryptography Engineering,Springer,Cham (SPACE 2014),2014:126-145.

[3] Zhang Wen-tao,Bao Zhen-zhen,Lin Dong-dai,et al.RECTANGLE:a bit-slice lightweight block cipher sui
Table for multiple platforms[J].Science China Information Sciences,2015,58(12):1-15.

[4] Thierry P Berger,Julien Francq,Marine Minier,et al.Extended generalized Feistel networks using matrix representation to propose a new lightweight block cipher:Lilliput[J].IEEE Transactions on Computers,2016,65(7):2074-2089.

[5] Beaulieu Ray,Treatman-Clark Stefan,Shors Douglas,et al.The SIMON and SPECK lightweight block ciphers[C].Design Automation Conference (DAC),52nd ACM/EDAC/IEEE,2015:1-6.

[6] Wang Peng,Feng Deng-guo,Wu Wen-ling.HCTR:a variable-input-length enciphering mode [C].China Information System Curricula(CISC 2005),Beijing,2005:175-188.

[7] Roberto Avanzi.The QARMA block cipher family[C].IACR Transactions on Symmetric Cryptology,2017,(1):4-44.

[8] Lars Knudsen.DEAL-A 128-bit block cipher[R].In:NIST AES Proposal,1998.

[9] Eli Biham,Alex Biryukov,Adi Shamir.Cryptanalysis of skipjack reduced to 31 rounds using impossible differentials [C].EUROCRYPT 99,LNCS 1592,1999:12-23.

[10] Jia Ping,Xu Hong,Lai Xue-jia.Impossible differential attack on LBlock-s[J].Chinese Journal of Electronics,2017,45(4):966-973.

[11] Chen Yan-qin,Zhang Wen-ying.Impossible differential attack on SIMECK32/64[J].Computer Engineering (CE),2017,43(4):141-144+153.

[12] Wei Yue-chuan,Pan Xiao-zhong,Rong Yi-sheng,et al.Impossible differential attack on block cipher PRINCE[J].Journal of Xidian University,2017,44(1):119-124.

[13] Hu Hong-jian,Jin Chen-hui,Li Xin-ran.Improved impossible differential attack of 7-Round on AES-128 [J].Journal of Cryptologic Research,2015,2(1):92-100.

[14] Fu Li-shi,Jin Chen-hui.Impossible differential attack of 13-Round on MIBS-128 [J].Journal of Electronics & Information Technology,2016,38(4):848-855.

[15] Zong Rui,Dong Xiao-yang.Meet-in-the-middle attack on QARMA block cipher [C].ePrint Archive,2016:1160.

附中文参考文献：

[10] 贾 平,徐 洪,来学嘉.LBlock-s算法的不可能差分分析[J].电子学报,2017,45(4):966-973.

[11] 陈彦琴,张文英.SIMECK32/64算法的不可能差分分析[J].计算机工程,2017,43(4):141-144+153.

[12] 魏悦川,潘晓中,戎宜生,等.对PRINCE分组密码的不可能差分攻击[J].西安电子科技大学学报,2017,44(1):119-124.

[13] 胡弘坚,金晨辉,李信然.改进的7轮AES-128的不可能差分攻击[J].密码学报,2015,2(1):92-100.

[14] 付立仕,金晨辉.MIBS-80的13轮不可能差分分析[J].电子与信息学报,2016,38(4):848-855.