20世纪30年代谢瓦莱对类域论的重建

阎晨光 王 涛

(河北科技大学理学院，石家庄 050018；中国科学院自然科学史研究所，北京 100190)

代数数论(Algebraic Number Theory)是用代数方法研究代数数域与代数整数环算术性质的数论分支，在20世纪有很大发展，类域论(Class Field Theory)则是其中体系最完美的一种[1]。类域论产生于19世纪后期的代数数论工作。1897年希尔伯特(D. Hilbert，1862～1943)出版《代数数域的理论》[2]，被后世称为《数论报告》(Zahlbericht)。此书一经出版便被数学界奉为圭臬，成为数学家研究代数的指路明灯，如阿廷(E.Artin，1898～1962)、哈塞(H.Hasse，1898～1979)等人都以此书为数论研究的肇始。之后希尔伯特和韦伯(H.Weber，1842～1913)描述了代数数域的阿贝尔扩张，并为类域论创立做好了铺垫。

1920年日本数学家高木贞治(T.Takagi，1875～1960)证明代数数域k的任意阿贝尔扩张K都可表示为k上的类域，并由此得到类域论基本定理，不过其证明非常繁复，还用到了解析方法[3]。后来阿廷最先开始简化证明，而完全消除解析方法的正是法国数学家谢瓦莱[4](C.Chevalley，1909～1984)。他在1940年完成了类域论的算术化工作，使类域论摆脱了繁杂的解析工具。[5]

谢瓦莱对类域论的纯粹算术证明和重建是类域论早期发展的关键环节，对谢瓦莱类域论工作的历史分析一直是代数数论史研究的中心问题之一。关于其工作的重要性，已有若干研究。高木贞治的学生、日本数学家弥永昌吉(S.Iyanaga，1906～2006)从代数数论发展史角度详尽地分析了谢瓦莱的工作[6]。弥永昌吉和哈塞是这段历史的亲历者，他们对谢瓦莱类域论工作的论述也颇有参考价值[7，8]。丢东涅(J.Dieudonné，1906～1992)等数学家也对谢瓦莱的相关工作多有评论[9]，分析了伊代尔概念及理论的数学意义[10，11]。中文研究并不多见，笔者曾论及谢瓦莱的类域论工作[12，13]，但因史料所限未能深刻挖掘其与哈塞和阿廷的关系；其他虽有述及类域论的中文著作对谢瓦莱的研究亦未深入[14- 16]。

2013年和2014年，笔者两度赴法，史料和研究基础大为充盈。在研读原始文献和数学家通信后，围绕谢瓦莱对类域论的算术化(Arithmetization)过程，笔者发现以下两个问题。

首先是谢瓦莱对类域论算术化的曲折历程。谢瓦莱工作中始终贯穿算术化主线，即消除类域论中的分析方法，代之以代数方法。但这种算术化并不是一蹴而就的，直到1934年谢瓦莱仍然怀疑是否能完全消除解析方法，哈塞也持有类似观点。但1940年谢瓦莱就彻底系统地用算术方法重建了类域论。这中间到底发生了什么？他克服了怎样的困难？目前大多数历史研究文献对此语焉不详，这是本文要探究的主要问题。其次是谢瓦莱在何种背景下如何完成了类域论的算术化。毫无疑问，谢瓦莱的工作与其20世纪30年代在德国的访学经历是分不开的。在研究问题和使用方法上，谢瓦莱都受到了哈塞、阿廷等人的影响。本文将谢瓦莱工作置于法德两国数学的发展背景中，综合考虑20世纪上半叶代数数论的发展趋势，以期更好地解释谢瓦莱对类域论进行算术化的原因和初衷。

1 谢瓦莱的数学圈子

谢瓦莱是法国二战后数学少壮派代表人物之一，其他重要人物有埃尔布朗(J.Herbrand，1908～1931)、韦伊(A.Weil，1906～1998)、丢东涅等。1926年17岁的谢瓦莱进入巴黎高师，跟随维西奥(E.Vessiot，1865～1952)、阿达玛(J.Hadamard，1865～1963)等数学家学习。由于一战影响，法国数学青黄不接，花甲之年的阿达玛建议谢瓦莱等年轻人到德国去学习数学。而德国当时有一批年富力强的数学家，如诺特(E.Noether，1882～1935)、阿廷、哈塞等人，他们主要从事与代数学相关的研究。诺特当时在研究“超复数系”，即结合代数，大大推广了以前的超复数系研究。阿廷则是抽象代数的另一位奠基者，著文虽少，但对布尔巴基学派影响颇深。1930年到1935年之间，阿廷作品中的思想方法和表述方式成为当时数学圈的“标准”。埃尔布朗、谢瓦莱和韦伊都直接受到他的影响。

谢瓦莱与哈塞和阿廷等数学家的关系代表了当时欧洲大陆数学发展的趋势与主要模式。发掘分析谢瓦莱与德国数学家的关系，将他与布尔巴基学派联系起来，可对谢瓦莱的数学背景有更多的认识和分析。相比诺特和阿廷，数学家哈塞并不为人们所熟悉，下面对哈塞生平做一简介。

1898年哈塞出生于德国卡塞尔，在一战中加入德国海军，退役后进入哥廷根大学，其老师有兰道(E.Landau，1877～1938)、希尔伯特、诺特和赫克(E.Hecke，1887～1947)等人。1920年哈塞到马堡大学跟随亨塞尔(K.Hensel，1861～1941)学习数学，受到其p-进数研究的很大影响，不久便创立“局部-整体原理”，并因此而名声大噪。1930年哈塞到马堡大学接替亨塞尔的教授职位，1934年接替从哥廷根大学辞职的外尔的职位。二战期间(1939～1945)他在柏林从事弹道学研究，1946年谋得柏林科学院的研究职位，1949年到洪堡大学任教，1950年到汉堡大学任教直到1966年退休。1979年哈塞在汉堡附近的阿伦斯堡去世[17]。

谢瓦莱与哈塞过从甚密，多有书信往还。依据目前掌握的书信资料，他们的通信始于1931年9月25日，止于1948年10月19日，按内容可粗略分为两类。

(1)对数学专业问题的探讨，这占据了通信的多半内容。大多数情况下，二人会在信中探讨数学细节，如1931年12月到1932年1月间两人曾就超复数系的理想类在信中进行深入交流([18]，8～10页)。

(2)谢瓦莱就学术相关问题征询哈塞的意见。这些问题涉及范围广泛，从如何修改论文到纪念埃尔布朗丛书的编纂出版，从论文投稿到在德国的访学安排，不一而足，谢瓦莱几乎是“事无巨细”地问计于哈塞。如1931年12月31日，为了出版一套纪念埃尔布朗的丛书[注]谢瓦莱与埃尔布朗是最要好的朋友，两人在大学时就已熟识。1931年7月埃尔布朗在一次登山事故中丧生。为纪念埃尔布朗及其数学工作，韦伊和谢瓦莱联合了巴黎高师数学系的一些毕业生，想出版一套丛书来纪念好朋友埃尔布朗。此部分可参考拙作[13]。，谢瓦莱在信中向哈塞约稿。([18]，8～9页)

当然，哈塞也对谢瓦莱青睐有加。在1934年11月16日的一封信中哈塞写道 ：

您能否在本学期到哥廷根来做一个报告……这有许多年轻数学家对您的研究感兴趣，……研究所的日常管理工作牵涉了很大精力，我很少有时间做数学研究。不过最近我又重新开始思考一些数学问题，……期待能与您在哥廷根当面探讨这些问题。([18]，33页)

从哈塞娓娓道来的语气，二人密切的科研关系和亲密的私人关系可窥一斑。

除哈塞之外，谢瓦莱还和其他几位德国数学家保持着学术联系。在1931年12月31日写给哈塞的信中，他写道 ：

我从诺特女士信中得知您正在研究超复数系的最大阶的理想类……([18]，8页)

1932年6月14日诺特在给哈塞的信中说 ：

今天谢瓦莱给我写了一封信，我想知道他在循环域中定义的范剩余符号与去年11月份我告诉他的是否一样。([19]，169页)

这些都显示谢瓦莱与诺特也保持着通信联系。

在当时的汉堡大学，以阿廷及其讨论班为中心，聚集了来自法国和日本的一批年轻数学家，也包括哈塞等德国数学家，良好的学术气氛令人羡慕。以阿廷和他的讨论班为媒介，谢瓦莱与这些数学家也保持着良好的学术关系。弥永昌吉曾回忆道 ：

在高木先生的推荐下，我到汉堡跟随阿廷做研究。当时埃尔布朗刚在一场事故中遇难，幸运的是我遇到了谢瓦莱。阿廷、埃尔布朗和谢瓦莱当时正在设法用更清晰的形式来论述类域论。阿廷先生特为此开设了一个讨论班，我和谢瓦莱都参加了。([20]，363页)

在讨论班上，谢瓦莱有什么好的建议，就会与阿廷和我联系，并在下次讨论班开始时与大家分享他的发现。也正是在这段时期，谢瓦莱重新构造了类域论的一般结构。([6]，52页)

弥永昌吉还提到 ：

一天晚上高木先生邀请一些数学家到他下榻的宾馆去 ：哈塞、谢瓦莱、诺特、Taussky、Tschebotarev、范德瓦尔登和几位日本数学家。(阿廷在外地)我至今仍对当晚愉快的气氛记忆犹新。([20]，364页)

综上，在1938年前往美国普林斯顿高等研究院之前，谢瓦莱与哈塞、阿廷、诺特等德国数学家以及高木贞治、弥永昌吉等日本数学家保持着密切的学术联系，这对他的数学生涯产生了很大影响。

首先，与德国数学家密切的学术联系促使谢瓦莱熟悉了德国同行的代数工作，尤其是哈塞、阿廷等人的工作。在德国访学期间，他与许多数学家建立了学术联系，并以此为基础直接进入代数学前沿——类域论。

其次，他的研究在多方面受到德国数学家的影响。从通信中可以看到，谢瓦莱从研究哈塞的工作而进入类域论，其构造的新的范剩余符号也仿照了哈塞的方法，还证明了两种符号的等价性；他的很多研究也直接来自与哈塞和诺特的通信，比如上述提到的关于范剩余符号的工作。他还常常在论文完成后将文稿寄给哈塞和诺特等人寻求意见。谢瓦莱与德国数学家的交流方式是当时法德数学家交流的主要方式之一，也从侧面反映了当时欧洲数学发展的一个特征。

2 谢瓦莱在类域论领域的工作

1930年到1940年的十年间谢瓦莱主要研究局部和整体类域论。谢瓦莱从追踪类域论最前沿的研究开始数学生涯[21- 24]。1931年他和埃尔布朗对类域论的存在定理给出了一个新的证明[25]，不久便初次尝试对类域论进行纯粹算术证明[26]。在法国国家科研中心资助下，1932年谢瓦莱到德国汉堡大学追随阿廷，后来又在马堡大学跟随哈塞学习，并开始博士论文的写作。受德国数学家(特别是哈塞)的影响，谢瓦莱定义了一种新的范剩余符号，并证明这与哈塞从局部出发给出的范剩余符号相一致[27]。1933年他在博士论文中将问题归结为证明循环域就是类域，并奠定了自成体系的类域论的基础[28]。1935年谢瓦莱与尼赫高恩[注]尼赫高恩在汉堡大学师从阿廷，1933年完成博士论文，之前在汉堡大学讨论班上与谢瓦莱相识。(H.Nehrkorn，1910～2006)首次成功地对类域论进行了纯粹算术的证明[29]，不过并未彻底算术化。1936年谢瓦莱引入了理想元(éléments idéaux)概念，并提到借助该概念可能完成类域论的算术化[30]。1940年他将理想元改造为伊代尔(idéle)，证明了伊代尔的主要性质，并借助伊代尔完成了类域论的算术化[5]。

这期间谢瓦莱在类域论领域共发表文章14篇[注]1954年谢瓦莱在日本名古屋大学访学时出版了一本讲义《类域论》(Class Field Theory)。该讲义主要内容是对类域论领域中的新方法——上同调方法进行概述，与20世纪30年代所使用方法有所区别，本文暂不涉及对该讲义的讨论。(表1)，其中“局部域和有限域的类域理论”(Sur la théorie du corps de classes dans les corps finis et les corps locaux)一文为其博士论文。对这些文章进行粗略分析，可以发现 ：

早期文章通常发表在《巴黎科学院通报》上，篇幅较短，内容可分为以下三类 ：一类是对类域论某些定理给出新的证明，另一类是证明前人给出的类域在新的定义之下也是类域，还有一类则是追踪类域论领域最新研究。

其次，文章通常由他独自完成，仅有的合作者为埃尔布朗和尼赫高恩，许多文章提到他受到了诺特、哈塞、阿廷等人工作的影响。

总体上他在类域论领域的工作分为两个时期 ：

(1)1929～1935年。这一时期他的工作较为零散，文章篇幅较短。也正是在这个阶段，他产生了将类域论算术化的想法，但只是对部分结论和定理完成了算术化证明。

(2)1936～1940年。这一时期他用纯粹算术方法证明了类域论主要定理，1936年引入理想元概念，1940年将其改进为伊代尔，并用纯粹算术方法重构类域论理论。

详细地看，其研究可以大致分成如下几个相继的阶段。

2.1 早期的零散工作

在学术生涯的早期，谢瓦莱从一些不太困难的小问题入手，开始证明类域论的主要定理。1929年他在《巴黎科学院通报》(Comptesrendusdel’AcadémiedessciencesdeParis)上发表了关于无限代数域的理想理论的文章[21]。1930年他仿照哈塞和施密特(F.Schmidt，1901～1977)的p-进数域的阿贝尔扩张理论，将哈塞之前证明的定理推广到了p-进数域[22]。在同时发表的另一篇文章里，谢瓦莱研究了范剩余理论，并将范剩余符号的主要性质推广到了相对伽罗瓦域上，但这样的推广对互反律却未能成功，原因是“对同一个域中不同的素理想来说，其范剩余符号是相同的。”([23]，428页)

1931年的短文“扩域和子域的类数的关系”可以看成是最直接进入到类域论领域的工作之一，谢瓦莱开门见山地写道 ：

本文要证明如下定理 ：假设k是代数数域，K是k的任意扩张。如果在k和K之间没有其他的k的非分歧的阿贝尔扩域，则K的类数可以整除k的类数。([24]，257页)

文中他还证明了一些推论，比如K/k为伽罗瓦扩张的情况。

表1 谢瓦莱在1940年前发表的有关类域论的文章和著作

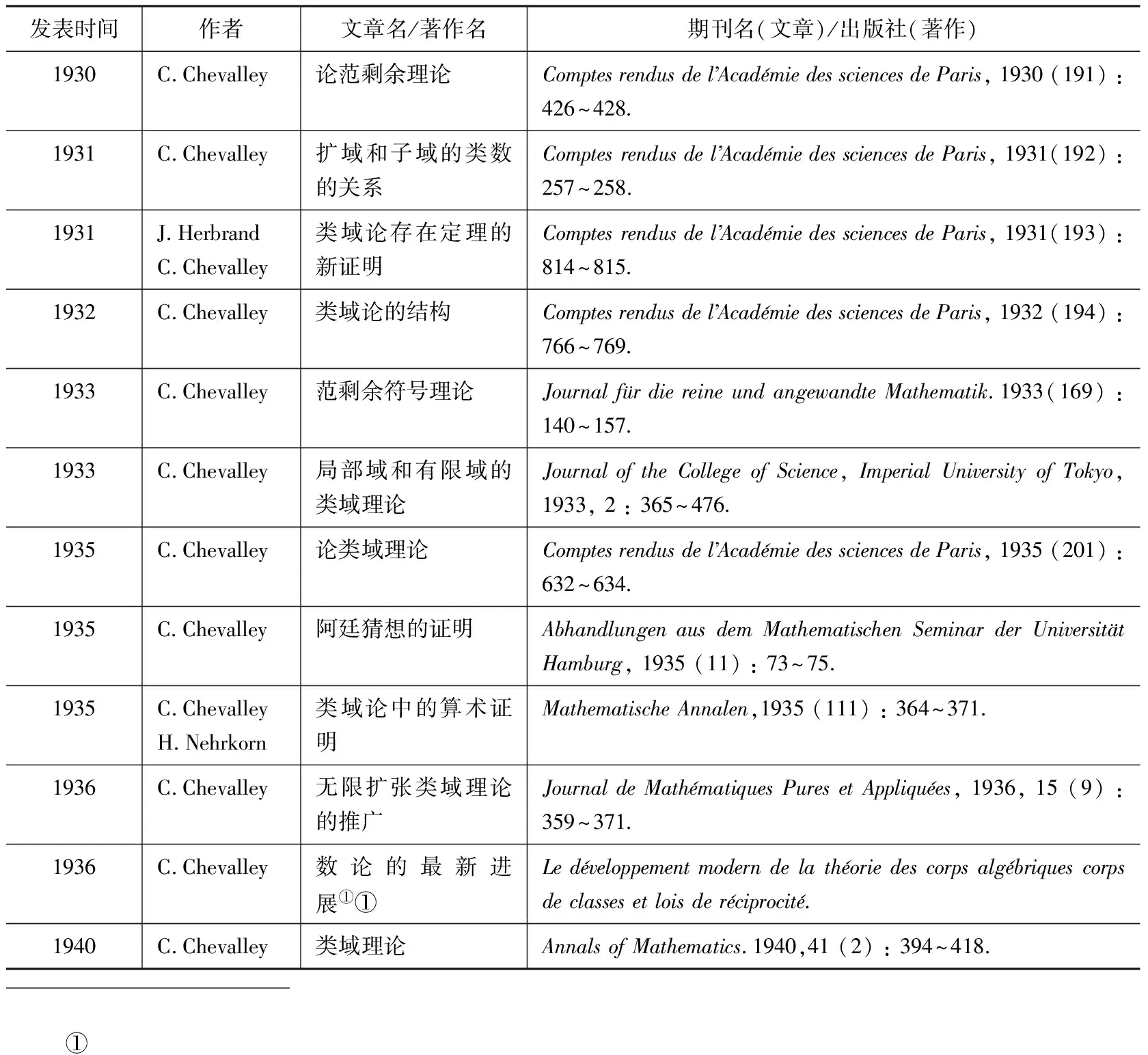
续表1

2.2 算术证明的初次“尝试”

1931年埃尔布朗和谢瓦莱对类域论中的存在定理给出一个新证明[25]，他们用商群的指标计算代替了原来的复杂计算，这堪称一个突破。不久谢瓦莱就尝试对类域论进行纯粹算术的证明。1932年他在“类域论的结构”一文中写道 ：

我对用纯粹算术的方法来证明类域论兴趣极大。本文将证明如果可以纯算术地证明给定域的每一个阿贝尔扩域都是类域的话，则目标就可以达成。([26]，766页)

这篇文章是谢瓦莱首次“尝试”不用解析方法而证明类域论的定理，这对数学家来说是一个新的方向。后面的一系列文章中，他开始逐渐向类域论主要定理的算术证明发起进攻。

2.3 对类域论主要定理的算术证明

从1931年到1932年，他对类域论的理论体系进行了极大简化，并完成了博士论文。与此同时，在参加阿廷和哈塞组织的讨论班时，谢瓦莱产生了借助理想概念的想法。在博士论文中，他完成了对类域论主要定理的算术证明，但在证明循环域是类域的结论时还是用到了解析方法。[注]对谢瓦莱的博士论文进一步的详细分析，请参看[6]。

博士论文答辩后，谢瓦莱给尼赫高恩写信通报了博士论文的主要结果。他们在1935年证明如果K是k的相对阿贝尔扩域，则K是k的类域，其主要目的是“展示类域论理论的哪些内容可以用纯粹算术的方法加以证明”([29]，366页)，这篇文章的接收日期是1934年12月31日，即1934年的最后一天。

就在一个多月前，1934年11月6日给哈塞的信中，谢瓦莱还写道 ：

……有可能将整个的类域理论纯粹算术化。……但对我来说，以我的理解，……，至少目前来看算术化的证明我认为仍然是有疑问的。([18]，30页)

值得注意的是哈塞在十天之后给谢瓦莱的回信中写道 ：

我越来越确信解析方法[注]哈塞信件的原文是analytischen Hilfsmittel。已成为类域论中必不可少的方法。([18]，32～33页)

可见，就在谢瓦莱进行类域论算术证明的同时，他和哈塞都认为彻底地将类域论算术化是不可能的。可是，仅仅不到一年之后，谢瓦莱就写道 ：

非常高兴地告诉您 ：我已经成功地用纯粹算术的方法将类域论的定理完全证明了。([18]，44页)

上面这封信写于1935年10月15日，那么到底这11个月间发生了什么？是什么令类域论的算术证明“柳暗花明又一村”呢？答案就是理想元的概念。在1935年10月的这封信中谢瓦莱还写道 ：“我使用的证明方法是理想的语言，这种方法很轻易地就可以转换为理想元的语言。” ([18]，46页)

2.4 理想元的概念

就在发出上面这封信的前一天，1935年10月14日，谢瓦莱将一篇短文提交给巴黎科学院[31]。他没有使用任何解析方法，其主要方法是群指标的计算。该文篇幅较短，仅不到3页，但在文章末尾他豪情万丈地宣称 ：

我们会证明所获得的结果将为整个类域论以及一般互反律提供基础，并且证明的过程将不借助函数论的方法。([31]，634页)

仅一天之后，1935年10月15日，他又写给哈塞一封长信，详细地解释了类域论纯粹算术证明的过程。他写道 ：

我认为借助理想元可以用一种更快的方式来证明您和Grunwald关于范剩余符号的结果。最终，存在定理也可以用一种算术的方式得到证明，而不需要使用算术级数的定理。([18]，46页)

他的主要工作是完成了对类域论中最主要的两个不等式h≥n和h

衷心祝贺您取得了如此重要的成果。您终于达成了梦寐以求的目标，我能想象得到您现在是多么幸福和自豪。我对您用理想元进行简化的方法非常感兴趣，如果您能将这些写成文章，我很高兴它们能在克雷尔杂志[注]即《纯粹数学与应用数学杂志》(Journal fur die Reine und Angwandte Mathematik)，由德国数学家克雷尔(A.Crelle，1780～1855)于1826年在柏林创办，通常也称作克雷尔杂志。上发表。([18]，47页)

不过，这篇文章最终于1936年在刘维尔杂志[注]即《纯粹与应用数学杂志》(Journal de Mathematiques Pureset Appliques)，由法国数学家刘维尔(J.Liouville，1809～1882)1836年在巴黎创办 ，通常也称作刘维尔杂志。上发表[30]，原因不得而知。文章中谢瓦莱引入了理想元概念，并定义了理想元的范剩余符号，他证明可以借助不同于(以往的)理想群的理想元来描述k的(有限或无限)阿贝尔扩张的特征。他还针对有限和无限阿贝尔扩张定义了推广的阿廷符号，并得到了这种推广的阿廷符号的性质。

2.5 类域论算术化的完成

从1936年到1940年，因二战欧洲局势逐渐动荡起来，谢瓦莱与哈塞虽仍有通信，但已不太频繁。这段时期双方共有11封通信(其中谢瓦莱发出7封信，哈塞发出4封信)，基本上没有讨论太多的数学内容。([18]，49～66页)

1940年谢瓦莱终于完成了类域论的算术化工作，文章开篇便对类域论工作进行了总结 ：

今天的类域论的表述较之前几年要简单多了，尤其是所谓“超越方法[注]原文是moyens transcendan。”的出现。然而，我觉得仍然有不少复杂研究本来是可以避免的。这篇文章唯一目标就是激起新的追求简洁和精简的工作。([5]，394页)

在这篇文章中，他用伊代尔的概念来替代经典的理想理论的语言，并在此基础上重建了整个类域论。

根据高木贞治的理论，代数数域k的任何阿贝尔扩张K都可表示为k上的类域。因此阿贝尔扩张成为类域论的关键，这也成为谢瓦莱的主要目的。这种目的当然受到传统的代数数论以及希尔伯特的类域论研究的影响，不过他更明确了类域论的研究目的是研究如何用基域k的性质来刻画其上的阿贝尔扩张K。在此研究目的下，文章共分为14部分，全文逻辑线路十分清楚[注]对谢瓦莱1940年工作的详细分析可参见拙作[12]，此处不再赘述。。

经过上述分析，可以得到如下结论。

首先，谢瓦莱对类域论的认识有一个缓慢的较为清晰的变化过程。在刚进入该领域时，他仅研究了类域论的一些简单命题和结论。当时他认为类域论的主要目的是素理想在扩域中的分解问题与互反律的关系，这显然受到代数数论中方法和主要论题的影响。之后在哈塞和阿廷等人的影响下，在与埃尔布朗的合作中，他开始研究扩域并尝试对类域论的理论进行算术化证明，此时其主要目的是想弄清楚类域论的哪些内容是可以算术化的，这在其博士论文中得到了很好的体现。此后，他的研究重心逐渐转移到类域论的算术化，但最初他和哈塞都对类域论的彻底算术证明持有怀疑态度。1936年他引入理想元概念，并借此完成了类域论存在定理的算术证明。最终，谢瓦莱在1940年将理想元发展为伊代尔概念，在此基础上完成了对整个类域论的算术化证明。

其次，伊代尔概念在他完成类域论算术化过程中占有很重要的作用，这个概念是他从前人关于理想的工作中借用的。他研究了伊代尔的性质，在伊代尔群中还定义了拓扑结构，研究了伽罗瓦扩张域的伊代尔群及其微分群的对应关系，并借此重建了类域论。

3 对谢瓦莱类域论工作的评价

对数学家的工作进行评价，通常做法是将其置于数学发展史中进行纵向剖析。一些研究已对谢瓦莱工作进行了较为深入的研究[8- 12]。作为上述研究的补充，下面主要分析不同时代数学家对其类域论工作的评价。

3.1 对谢瓦莱的已有评价

谢瓦莱工作中最先引起数学界注意的是埃尔布朗和他1931年发表的文章[25]。1931年6月16日阿廷在写给哈塞的一封信中说道 ：“埃尔布朗和谢瓦莱对类域论给出了全新的简化，我非常激动。”([32]，380页)得知谢瓦莱和埃尔布朗的上述工作后，诺特也给予了较高的评价，她在给哈塞的信中写道 ：“指数计算变得越来越简单清楚了，太好了!”([19]，156页)

1932年谢瓦莱首次尝试对类域论给出算术证明，诺特在1933年5月10日给哈塞的信中说 ：“近日谢林[注]谢林(O.F.G.Schilling，1911～1973)是诺特的博士生，诺特到美国后便师从哈塞。在给我的信中介绍了谢瓦莱的一种新的超复数方法，这正是我所期待的，对此我非常兴奋。”([19]，188页)1933年6月27日诺特又写道 ：“我现在想知道 ：谢瓦莱是否将类域论的全部内容都算术化了？还是我理解错了？”([19]，193页)

实际上，谢瓦莱1932年的这篇文章并没有真正将类域论完全算术化。上文提及，1934年谢瓦莱和哈塞都认为完全将类域论算术化证明是令人怀疑的，或者说解析方法在类域论的证明中是不可缺少的，而诺特在同时期也有同样的认识。1934年诺特曾经在给哈塞的一封信中提到即使是最简洁的途径也必须要将谢瓦莱的方法和一些超越方法综合起来才行。([19]，213页)

此外，阿廷也对谢瓦莱的类域论工作非常推崇，弥永昌吉回忆道 ：

高木贞治在汉堡遇到了阿廷。阿廷向高木推荐了谢瓦莱的博士论文，称之为“第一流的工作”，建议高木推荐它在《东京大学学报》上发表。不久谢瓦莱的博士论文就跟高木先生的文章在《东京大学学报》的同一期上发表了。([20]，364页)

作为希尔伯特的学生，高木贞治也对谢瓦莱(和埃尔布朗)在类域论方面的简化工作给出了一些评述[33]。

从以上分析可以看出，总体而言，哈塞、诺特、阿廷以及高木贞治等数学家对谢瓦莱在类域论领域的工作一贯持有较为肯定的态度，他们也都与谢瓦莱长期保持着较为密切的学术联系。

1948年前苏联出版了一套丛书“三十年来的苏联数学”[34]，系统论述了俄国十月革命之后苏联数学的发展，其中《代数学》一册对类域论进行了简要概括。书中认为阿廷的互反律推动了类域论的进一步发展，而哈塞和谢瓦莱相继改造了类域论，后者提出了不用超越方法而建立类域论的问题。书中特别提到谢瓦莱的“理想”概念[注]这是该书的一个错误。实际上谢瓦莱并不是引入了理想概念，而是引入了理想元的概念，理想的概念是戴德金在1871年针对数论给出的。和p-进代数域的相对阿贝尔扩张。([34]，14～15页)

作为谢瓦莱的好友，布尔巴基学派的创立者之一的数学家丢东涅的认识和评论则相对准确一些。丢东涅在纪念谢瓦莱的文章中写道 ：

在博士论文中，谢瓦莱奠定了独立的局部类域论的基础，……。他证明可以直接从p-进域出发考虑其阿贝尔扩张。这样得到的定理比整体类域论的要简单。……接下来谢瓦莱致力于直接从类域论中消除解析方法，并试图将类域论推广到有理域的无限次扩张上。在引入伊代尔概念后，他成功了。伊代尔的概念成为了代数数论的重要概念，这是第一个明确的从局部过渡到整体的实例。([9]，1～4页)

丢东涅对谢瓦莱类域论的工作评价很高，但他对谢瓦莱1940年之后群论和代数群方面工作的论述仍然占了文章的一大部分，他认为“谢瓦莱对数学的最重要贡献当属他在群论方面的工作”([9]，4页)。在数学家丢东涅看来，谢瓦莱1930～1940年十年间关于类域论的工作似乎并不是他最重要的数学工作。

3.2 对谢瓦莱工作的重新评价

从历史发展来看，不应将数学家在不同时期、不同领域的成果简单对比，而应将其放入所属领域，从分支、领域的发展史来评判其重要性，综合考虑数学家在不同领域所做工作的重要性，而不是限于单纯的比较研究。在这个目标的指引下，我们做出如下分析。

首先，毋庸置疑是谢瓦莱开创了类域论研究的新局面，他不仅引入了伊代尔概念，给出了纯粹的局部类域论，在伊代尔基础上重建了类域论理论。更重要的是，他研究了伊代尔的拓扑性质，也首次成功地在代数数论中引入拓扑方法。

其次，对谢瓦莱工作进行全面评价，需要将类域论工作与他在20世纪二三十年代的经历联系起来。谢瓦莱曾到德国游学，其类域论工作也在一定程度上带有德国数学的印记，体现了法德数学交流的时代特征。

(1)哈塞在谢瓦莱类域论工作中扮演了重要的角色，或者可以说没有哈塞就没有谢瓦莱的类域论工作。

1934年哈塞在哥廷根大学开设的课程吸引了许多年轻数学家，他经常在信中与德国数学家讨论代数学最新进展，并随时通过信件将这些通报谢瓦莱，与哈塞的通信成为谢瓦莱在文章之外获得研究动态的主要渠道之一。相较于正式发表的论文，信件的信息量更大，约束也更少。与哈塞的通信对谢瓦莱的类域论研究是非常重要的。

一方面，谢瓦莱曾在马堡大学跟随哈塞学习了两个学期，之后二人信件往来频繁，这对谢瓦莱无疑是最直接的鞭策和鼓励。另一方面，哈塞对谢瓦莱很是欣赏，尽一切可能帮助他，比如将他的文章推荐至克雷尔杂志[注]当时哈塞正是克雷尔杂志的3位主编之一，另外两位分别是亨塞尔和史列辛格(L.Schlesinger，1864～1933)。，这对初出茅庐的年轻人也是至关重要的。通过通信我们还能推断 ：哈塞是谢瓦莱与德国代数学家联系的主要纽带，谢瓦莱从哈塞处获知了类域论领域许多前沿信息。

(2)诺特应被视为谢瓦莱类域论工作的推动者之一。

20世纪20年代开始，诺特在代数领域得到一些有影响力的结果，并因此被称为“代数学之母”。许多数学思想都源于诺特，她对数学，尤其是代数学影响甚为深远。[35]20世纪20年代后期，世界各国的数学家都到哥廷根来追随诺特，比如拓扑学家亚历山大洛夫(P.Alexandrov，1896～1982)和霍普夫(H.Hopf，1894～1971)在哥廷根大学访学期间曾多次与她交谈，他们的拓扑工作受到她很大的影响。此外，诺特还对哈塞和布饶尔(R.Brauer，1901～1977)在代数学方面的工作有直接的影响，比如三人对代数学主定理的证明[36]。后来名噪天下的布尔巴基学派的工作也正是建立在诺特和阿廷的思想之上[37]。从这个意义上来说，诺特可以被视为当时德国数学圈的中心之一。

诺特非常关心谢瓦莱和埃尔布朗的类域论工作，并曾写信向哈塞询问谢瓦莱类域论工作的细节。通过谢瓦莱和哈塞的通信，我们还知道谢瓦莱与诺特也有直接的通信，二人在信中经常就某些数学问题展开讨论，诺特也对谢瓦莱的研究提出了许多建议。因此，诺特是谢瓦莱对类域论进行算术化的有力推动者之一。

第三，当时的法国数学主流是函数论研究，谢瓦莱关于类域论的工作在法国并未产生很大影响，这一点从《巴黎科学院通报》上发表的文章也可窥一斑。1930年该期刊上只有一篇代数学方面的文章，而函数论方面的文章则有39篇。1931年两个领域的文章分别有7篇(4篇出自谢瓦莱和埃尔布朗)和24篇。尽管谢瓦莱在《巴黎科学院通报》上发表了几篇文章，但篇幅都不太长，(特别是在法国)没有引起什么大的影响[注]除了引起诺特、哈塞、阿廷等少数德国数学家注意外。。反而是他发表在德国期刊上的其他几篇文章，比如1933年在哈塞的推荐下发表在克雷尔杂志上的文章(18页)，1934年在高木贞治的推荐下发表在《东京大学学报》上的文章(长达112页)，不仅篇幅较长，产生的影响也要大得多。但由于当时法国数学的主流是函数论和分析学，谢瓦莱关于类域论的工作在法国国内并未引起多大的影响，反倒是其在20世纪30年代参与发起的“新秩序”政治组织在法国引起了一些影响。

第四，布尔巴基学派完全是数学家自发地振兴法国数学的产物。笔者原本“设想”是法国政府或数学界有组织地将韦伊、埃尔布朗、谢瓦莱等人送到德国去学习数学。如果是这样，这些学者返回国内势必会在数学界引起某些反响，他们在国外游学期间所取得的成果当会受到国内数学界的关注。然而，事实并不是这样。不仅法国数学界并没有对这些年轻数学家的成果给予更多的关注，就连这些“海外学者”的归国也并未在巴黎的数学圈引起更多的注意，联想到后来布尔巴基学派的名噪天下，这的确有些不可思议。

4 结 语

从数学发展史上看，不同的数学发展时期有不同的发展主题(topic)和特征(character)，这既受到数学大环境客观因素的影响，也受到不同地域的数学家主观因素的影响，是主、客观因素综合作用的结果。谢瓦莱刚进入类域论领域时正处于两次世界大战之间，也正是数学酝酿新事物、新思想、新变革的年代。

20世纪头20年，代数数论研究中出现了许多新思想和新方法，如赋值和局部域理论、局部-整体原理、p-进分析、几何和解析方法的引入等。在类域论领域，希尔伯特的学生、日本数学家高木贞治证明了类域论基本定理，但其方法过于依赖解析方法，因此阿廷便开始努力将其代数化。20世纪20年代也正是阿廷创造性的高峰期，他不仅着手推广类域论的结果，还证明了一般互反律。哈塞则早在1920年便证明了“局部-整体原理”，并在不久后跟随亨塞尔的p-进数工作开始了对局部类域论的研究。同时期诺特则主要关注超复数系的研究，将其与弗洛宾尼乌斯表示论联系起来，形成了系统的代数理论。

正是在此基础上，埃尔布朗和谢瓦莱跟随着哈塞和阿廷的工作并在诺特等人的影响下，对类域论产生兴趣，并开始对类域论进行算术化证明。从1929年到1940年谢瓦莱一直坚持不懈地试图从类域论中消除解析方法，这个过程是一个缓慢的循序渐进的过程。

单纯从数学角度来说，谢瓦莱开创了类域论研究的新局面。他引入了伊代尔的概念，研究了伊代尔的拓扑性质，并借助伊代尔的概念将类域论完全算术化。他所使用的方法体现了哈塞创立的局部-整体原理，伊代尔概念无疑是对哈塞的局部-整体原理最好的诠释，丢东涅称之为“第一个明确的从局部过渡到整体的实例”。谢瓦莱继承了前人的研究路线，但引入伊代尔并借助微分群使他突破了前人研究路线的限制。他的研究目的更加明确，研究对象以无限阿贝尔扩张为主，并将经典类域论的主要定理一举囊括，这种从特殊到一般情形的发展不啻是数学发展中最经典最鲜明的线索。特别是谢瓦莱对类域论的算术化过程与数学家对互反律的研究交织在一起，不仅从互反律汲取营养，其方法也深刻地影响了互反律，并与朗兰兹纲领这一数学史上最著名的理论有密切联系。这启示我们应继续深入挖掘谢瓦莱的类域论工作的历史价值，将其放到学科交叉背景下，探讨其对现代数学的影响。