基于S变换的振动信号时频特征分析
李 丽,刘 剑,闫亚荣
(1.山西省地震局,山西 太原 030021;2.太原大陆裂谷动力学国家野外科学观测研究站,山西 太原 030025;3.太原理工大学矿业工程学院,山西 太原 030024;4.运城市地震局,山西 运城 044000)
0 引言
2013年11月10日和2014年1月8日,山西南部至晋陕交界先后发生2次大范围的振动事件,主要表现为万荣、闻喜、永济、侯马、垣曲等地民房窗户持续作响,持续时间约10 s左右,但人无震感,陕西合阳台和山西南部多个测震台站都记录到振动波形。振动信号是典型的非平稳信号,时频分析能够很好地反映非平稳信号在时间和频率轴的能量强度分布,更好地突出信号局部特征,在地震波资料和前兆数据中得到广泛的应用[1-6]。为全面了解山西南部大面积振动事件信息,运用S变换方法对每个台站记录到的波形进行计算分析,获取振动信号时频特征。
1 研究方法
常用的时频分析方法有傅立叶变换、小波变换、Wigner-Ville时频分布、S变换等[7]。传统的傅立叶变换是一种全局变换方法,无法表征频率随时间变化的局部特征。因此在傅立叶变换的基础上,发展一些新的信号处理方法,如短时窗傅立叶变换、小波变换等,但是这些理论各有不足,不能突出非平稳信号的局部信息。为此,Stockwell[8]提出新的时频方法—S变换,该方法是介于短时窗傅立叶变换和小波变换之间的一种非平稳信号分析和处理方法,克服另两种方法的缺点,具有较高的时频分辨率。
Stockwell[8]提出的S变换定义为:
假设信号s(t)∈L2(R),(L2(R)表示能量有限函数空间),定义:
(1)
式中:τ,f分别表示时间和频率,均为实数。
反变换为:
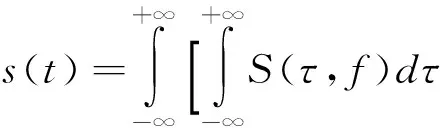
(2)
(2)式是以Morlet小波为基本小波的连续小波变换的延伸。
基本小波是由简谐波与高斯函数的乘积构成,定义为:
(3)
S变换克服短时窗傅立叶变换不能调节分析窗口频率的问题,引入小波变换的多分辨分析,且与其傅立叶谱保持直接的联系,使得基本小波不必满足容许性条件等特征[9]。该方法不存在交叉项的影响,具有较高的时频分辨率。
2 数据资料
记录到振动信号(见第2页表1)的陕西合阳和山西南部测震台,均采用数字化地震观测仪器,记录频带范围为0.05~60 Hz,采样率均为100。由记录到振动波形事件的台站分布图(见第2页图1)看出,2013年、2014年的两次振动事件影响范围较广,西起陕西合阳,东至山西沁水,东西相距约200 km,主要集中在临汾南部和运城地区[10]。本文主要针对记录振动波形信噪比较高的合阳、万荣和沁水台三分量进行时频分布计算。

表1 振动事件统计表Table 1 Statistics of vibration events
3 特征分析
从图2看出,两次振动事件被同一个台站相同分量记录的波形时频分布差异较大,三分量无明显的分布规律。振动波列能量随频率和时间展布一般在3~20 Hz,能量优势频段(主频)在每个分量差异较大,不同事件在同一个台站能量优势分布及频率分布范围也不同。整体而言,合阳台三分量记录的2013年振动波列能量的频率分布范围和持续时间比2014年的相对较宽、较长;2013年的频率分布范围为5~15 Hz,其中东西和垂直两分量能量的频率分布较低,主要集中在5~8 Hz;2014年的频率分布相对较高,主要集中在10~15 Hz。

图1 记录到振动波形事件的台站分布Fig.1 Distribution of stations recording vibrational wave events

图2 山西合阳台三分量时频分布图Fig.2 The time frequency distribution of the three components of Heyang station in Shanxi
第3页图3是台站记录的2013年11月10日大面积振动事件,台站顺序根据接收振动信号的先后进行排列,可以看出每个台站记录到振动波形的能量分布和衰减情况无显著的规律性特征。最早记录到振动信号的合阳台,两水平分量的能量频率分布范围较大,一般在5~20 Hz,高频能量持续时间较长,约10 s左右;其后记录到的万荣台,两水平分量波形的波峰较多,能量主要集中在低频,范围为3~6 Hz,优势频段在5 Hz左右,由于携带能量较多的波峰增多,低频能量持续时间较长,约15 s左右;最晚记录到的沁水台,两水平分量记录的波峰均为1个,在波峰处能量较强,衰减较快。沁水台能量频率随时间分布不同于合阳台和万荣台,高频成分较多,主要集中在15~25 Hz,持续时间较短,约3~5 s。

图3 合阳台、万荣台和沁水台两分量时频分布图Fig.3 The time frequency distribution of the two components of Heyang station, Wanrong station and Qinshui station
4 结论
对山西南部大面积振动事件波形的时频特征分析,得出以下结论:
(1) 无论是同一振动事件被不同台站记录,还是同一个台站记录不同的振动事件,波形在每个台站的形状特征都有很大差异,一般单波峰最大能量持续时间较短,双波峰或三波峰以上的能量持续时间较长且频率分布范围较大。
(2) 接收波形信号时间先后不同的台站,能量并未发生明显的衰减,除能量频率分布范围和持续时间不同外,无其他显著差异。
(3) 利用S变换方法研究山西南部大面积振动波形时频分布特征,有助于进一步了解振动事件属性特征,为研究振动事件产生的原因提供更多的参考依据。
[1] 刘希强,沈 萍,山长仑,等.数字化地震波形资料的时频分析方法及应用[J].地震工程学报,2004,26(2):118-125.
[2] 张 帆,钟羽云,朱新运,等.时频分析方法及在地震波谱研究中的应用[J].地震地磁观测与研究,2006,27(4):17-22.
[3] 姚家骏,杨立明,冯建刚,等.常用时频分析方法在数字地震波特征量分析中的应用[J].地震工程学报,2011,33(2):105-110.
[4] 李文军,张 晶,刘 琦,等.2012年印尼8.6级地震应变地震波的Hilbert-Huang时频分析[J].地震,2014,34(2):45-54.
[5] 郑建常,徐长朋,赵金花,等.基于S变换的矿山地区地震波形时频分析[J].地震地磁观测与研究,2014,35(5):8-14.
[6] 刘素珍,李自红,张淑亮,等.2014年大同地电阻率NW测项异常分析[J].地震地磁观测与研究,2016,37(2):104-110.
[7] 张贤达,保 铮.非平稳信号分析与处理[M].北京:国防工业出版社,2001.
[8] Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing,1996,44(4):998-1001.
[9] 焦叙明.时频分析及其在地震资料处理分析中的应用[D].山东青岛:中国海洋大学,2007.
[10] 扈桂让,李自红,闫小兵,等.韩城断裂晚第四纪活动性研究[J].地震地质,2017,39(1):206-217.

