基于测井曲线物理建模技术在煤系岩相分析中的应用

汤红伟

(中煤科工集团西安研究院有限公司，陕西 西安 710077)

0 概况

袁大滩井田位于陕北侏罗纪煤田榆横矿区东北部，榆溪河以西，无定河以北，古长城西北处。井田内地表被第四系松散沉积物覆盖。钻孔揭露区内地层由老至新依次为：三叠系上统永坪组，侏罗系下统富县组、中统延安组、直罗组、安定组，白垩系下统洛河组，第四系中更新统离石组、上更新统萨拉乌苏组及全新统风积沙。

本区延安组煤层发育，可采煤层7层，其中主要可采煤层为2号、3-1、4-2、5号煤层，2号煤层厚度较大。

2号煤层顶板主要充水水源一是洛河组与安定组碎屑岩类风化壳孔隙裂隙承压水，其岩性主要为砂岩，厚为30～60m；二是安定组砂岩孔隙裂隙承压水岩性以中细粒砂岩为主，厚为12.46～87.33m，平均厚50.61m。

近年来，煤层顶板水害已成为制约袁大滩煤矿安全生产的重大隐患，为了研究2号煤层顶板砂岩含水层富水性发育规律，开展了对2号煤层顶板岩性的精细解释。

1 测井方法

由于井田内的测井曲线不全，仅有自然伽马、自然电位、电阻率和密度测井，尤其缺乏声波测井资料。

为准确识别煤层顶板岩性，克服测井资料不全和录井岩相不准等技术瓶颈，本文将测井地层评价和岩石物理建模作为一个整体进行研究(图1)。

应用现有的测井曲线对煤层顶板岩性进行精细解释，获得泥质含量、孔隙度、饱和度等地层参数，然后将该地层参数作为岩石物理建模的输入，优选合理的岩石物理模型和参数，最终获得正演速度、密度等弹性参数，以应用于后续的煤层顶板岩性预测研究。

图1 技术研究流程Figure 1 Technical research flow

2 测井精细解释评价

基于后续岩石物理正演纵波速度和地震反演项目研究的需求，对测井资料进行储层参数评价。由于地层较浅，主要分析泥质含量和孔隙度的特征变化，流体部分按照饱含水进行处理。

①泥质含量的计算

式中：SH为泥质指数；GR为自然伽马测井曲线；GRmin为纯砂岩自然伽马曲线值；GRmax为纯泥岩自然伽马曲线值。

式中：VClay为泥质含量；GCUR为地层参数。

②孔隙度计算

由于研究工区内资料有限，仅有密度孔隙度曲线，因此孔隙度运用密度曲线计算，计算公式：

式中：PHID为密度孔隙度；DENm为骨架密度；DEN为密度测井曲线；DENf为流体密度；DENsh为泥岩密度；Vclay为粘土含量。

利用上述方法计算泥质含量和孔隙度，获得岩石的体积模型，然后根据泥质含量和孔隙度进行岩性划分(图2)，岩性划分标准为：VClay>0.3，砂质泥；VClay<0.3，PHID<0.1，细砂岩；Vclay<0.3，PHID>0.1，中砂岩；煤层：DEN<2.1g/cm3。

图2 K1-1井的测井解释体积模型Figure 2 Well K1-1 well logging interpretation volume model

在岩石物理建模过程中，应用xu-white模型[1]计算干岩骨架弹性模量，利用Batzle-Wang模型计算流体的弹性模量，采用Gassman方程进行流体替换分析。在实际分析过程中需要注意以下几个关键点。

①岩石物理模型可选种类很多，但都有其应用的适用条件。通过密度曲线计算的孔隙度值域在5%～20%，因此利用针对砂泥岩二相介质的xu-white方法进行干岩骨架模型的建立是合适的。

②Alpha参数的调整。储层中不同孔隙空间类型，通过椭球体几何空间进行刻画，椭球体的空间短轴与长轴之比定义为孔隙空间宽长比，用Alpha来表示。当Alpha越小，孔隙形状越细，越接近细长型裂缝型孔隙；当Alpha越大，孔隙形状越接近圆形。通过对石英矿物和粘土矿物的Alpha值进行扰动分析，分别给予不同的宽长比值，其中粘土的Alpha为0.04，石英矿物的Alpha值为0.12。

依据上述过程和方法，建立岩石物理模型(图4)，并利用该模型参数正演密度、速度等弹性参数曲线。

图5为岩石物理正演曲线(左图为K1-1井、右图为K1-3井)，每张图中从左至右分别为，第一列为岩性曲线：蓝色为自然伽马，橙色为自然电位；第二列为深度道；第三列为测井电阻率，第四列为正演的纵波时差；第五列曲线： 红色为正演密度，黑色为实测的密度曲线；第六列为正演横波时差；第七列为纵波阻抗。

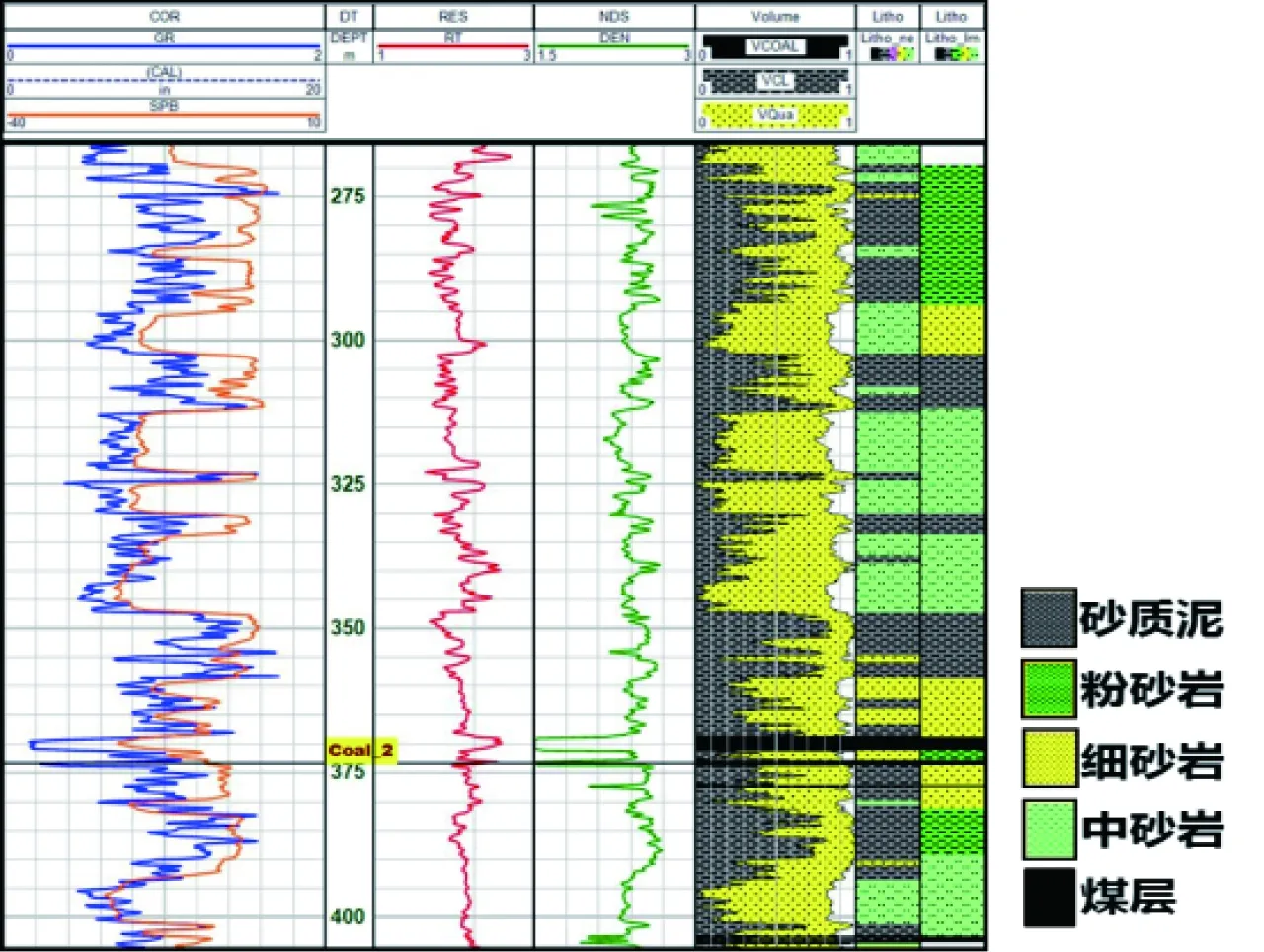
图3 K1-3井测井解释结果和录井结果对比(左侧为测井解释岩性划分，右侧为录井岩性划分)Figure 3 Comparison of well K1-3 well logging interpreted and geological logging results

图4 岩石物理建模技术流程图Figure 4 Rock physical modeling technical flow

通过对比分析，正演密度曲线与实测密度曲线(图5)误差小于8%，表明密度正演结果可靠。但是正演的速度曲线还需要其他方法进行可靠性验证。进行正演速度曲线可靠性分析的方法是进行合成记录标定，可以对比地震速度和正演速度的一致性，图6为上述二井的合成记录和地震对比图6，由此可以看出：

①时间值是利用计算的声波时差进行积分获得的，没有任何的拉伸压缩调整，说明速度的绝对值和地震速度匹配一致；

②合成记录的振幅和地震振幅的相对关系基本一致，相关系数高达90%，说明岩石物理模型正演的速度的相对关系是正确的。

在此基础上，将纵波速度和密度乘积计算纵波阻抗曲线，然后分岩性建立直方图(图7)。明显地，煤层速度最低，中粒砂岩低于泥质砂岩，最为致密的细粉砂岩阻抗最高。因此， 可以利用纵波阻抗很好地区分不同的岩相。

图5 岩石物理正演曲线Figure 5 Rock physical forward traces

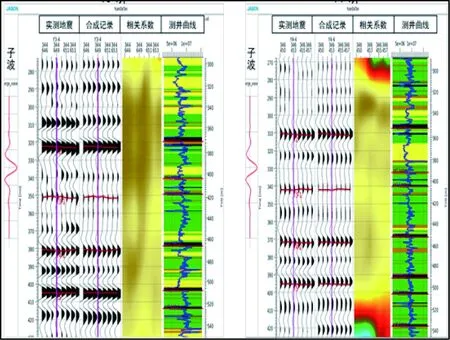
图6 利用正演结果进行合成记录标定Figure 6 Synthetic record calibrations through forwarded results

图7 分岩相纵波阻抗直方图Figure 7 Lithologic facies based compressional wave impedance histogram

3 结论

在声波曲线缺失的条件下，利用精细测井解释和岩石物理建模，可以获得正演的纵波速度曲线，利用该曲线进行井震标定，通过合成记录和地震的对比可以确定正演曲线的准确性。同时，在获得声波曲线的基础上，计算纵波阻抗，进行岩石物理分析，指示该区域纵波阻抗可以区分中粒砂岩和细粉砂岩。因此，在后续的研究中，利用叠后的波阻抗反演可以解决岩性划分问题。

[1]Xu S, White R E. A new velocity model for clay- sand mixtures[J]. Geophysical Prospecting, 1995, 43: 93-118.

[2]Xu S, White R E. A physical model for shear-wave velocity prediction[J]. Geopysical Prospecting,1996,44:687-717.

[3]Batzle M, Wang Z. Seismic properties of pore fluids[J]. Geophysics,1992,57:1396-1408.

[4]GassmannF.Elasticity of porpousrock[J]. Viertel-jahrschrift der NaturforschendenGescllschaft in urich, 1951,96:1-21.