基于滑模控制的三相PWM整流器结构设计与性能仿真
高日辉,陈 燕,马春燕,窦银科
(太原理工大学 电气与动力工程学院,太原 030024)
PWM整流器能够实现网侧电流波形正弦化、在功率因数为1的条件下运行以及能量的双向传输,所以PWM整流器实现了真正的“绿色电能变换”[1]。
目前,PWM整流器通常采用的控制方式是在d-q同步旋转坐标系下电压外环和电流内环相结合的双闭环控制,系统控制器的设计则是基于PI控制来实现。使用这样的控制方式时,PI控制器容易实现,整流器的稳态性能好。但是,PI控制系统的控制作用总处于滞后状态,想要使整流器控制系统保持好的动态性能很难。另外,要使系统电压电流同时获得较好的输出特性,必须控制好整流器的电压外环,电压外环的抗扰性好、精度高、输出稳定是网侧电流获得良好性能的基础。在采用PI控制设计的整流器电压外环中,虽然做了一些必要的假设和近似,但是由于传递函数是时间函数,其可变性强,设计出理想的控制器依然比较困难,同时在负载出现扰动的情况下输出电压超调量大,而且无法在短时间内恢复[2-3]。
采用滑模控制设计控制系统时,无需考虑被控系统参数和外界扰动,所以其对被控系统参数和其它不可预知的干扰有很强的鲁棒性。本文在PWM整流器的控制系统设计中摒弃PI控制而引入滑模控制。仿真结果表明:该方案所设计系统的输入电流波形为正弦,功率因数接近单位功率因数,同时,与基于PI控制的整流系统相比,系统能更好地适应负载的扰动和非线性变化[4]。
1 PWM整流器的建模[5]
如图1所示,ex是三相电源的相电压;ix是三相电源的相电流,x=a,b,c;RL是输出负载;C是直流滤波电容;L是交流侧滤波电感;R是滤波电感的寄生电阻。

图1 三相PWM整流器拓扑结构图Fig.1 Topology structure diagram of three-phase PWM rectifier
设三相电源的输出波形为理想的正弦波,定义三相桥臂的逻辑开关函数Sk为:
(1)
式中,k=a,b,c.
由图1并结合基尔霍夫定律推出在三相静止坐标系下PWM整流器的数学模型为:
(2)
对方程组(2)中的各式做“等功率”坐标变换,得到在d-q坐标系下的PWM整流器数学模型为:
(3)
2 电压环控制器设计
由式(3)可以推出系统处于稳态时状态空间方程的能控标准型为:
(4)

(5)
式中:k,α1,α2为放大增益,目的是为了在确保系统稳定的情况下获得理想的动态响应;系数β(β=α2/α1)是滑模控制的反馈系数,与输出直流电压vdc的一阶响应相关。 由式(4)和式(5)得出:

(6)

(7)
由于在系统方程经过坐标变换后,系统的滑模函数中会含有两个非线性时变变量Sd和Sq.而整流器控制的主要目的是使系统在设定的滑模面上滑动,要使系统状态轨迹运动于设定的滑模面上,就需要知道理想情况下Sd和Sq的值。由式(3)得出:
(8)
式中,dvdcref/dt=0.
由理想滑模面s1(eiq,t)=0,s'1(eiq,t)=0及式(4)得出:
(9)

(10)
把式(10)代入式(7)得:
(11)
令:
(12)
那么,由式(12)和iqref=0就得到了满足电压输出要求和获得单位功率因数的电压外环控制方程:
(13)
3 电流环控制器设计
在现实的控制系统中,由于控制器性能以及系统能量的限制,滑模控制开关切换过程并非理想切换,因此,在滑模控制中都会存在有抖振问题[8]。
本文采用指数趋近律的方法设计系统控制率从而来达到削弱系统抖振的目标。指数趋近律为:
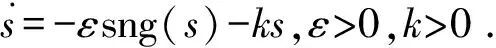
(14)

采用指数趋近律令:
(15)
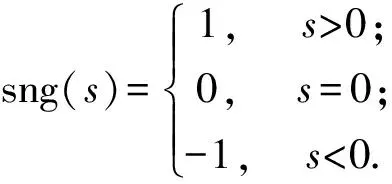
由滑模面函数式(13)得:
(16)
由d-q坐标系下的整流器数学模型式(3)得:
(17)
联立式(15)(16)(17)解得:
(18)
接下来由vd=vdcSd,vq=vdcSq得电流环的滑模控制律为:
(19)
由图2可以看出,整个控制系统由电压环和电流环构成。首先,在电压环中,由直流输出侧的电压信号采集电路采集到直流输出电压vdc,把它与系统给定的直流电压vdcref比较做差后进入滑模控制单元进行调制,得到d轴参考电流idref,idref和系统给定的q轴电流分量iqref分别与三相输入电流经坐标变换后的电流分量id,iq比较做差后进入滑模控制单元进行调制,得到在d-q坐标系下的电压控制信号Vd和Vq,这两个电压控制信号再经坐标变换为α-β坐标系下的电压控制信号输入到SVPWM模块从而激发脉冲信号触发整流器工作。
4 仿真比较与分析
为了对本文所提控制方案的动态和静态性能进行验证,采用Matlab/Simpower工具箱分别对基于PI控制和滑模控制的三相PWM整流器建立了仿真模型并进行仿真实验。系统仿真图如图3所示。表1列出了仿真实验所选取的整流器主要参数。
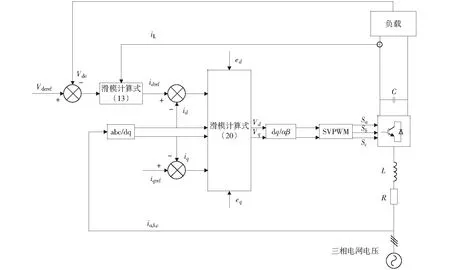
图2 三相PWM整流器滑模控制系统结构Fig.2 Control system block diagram of three-phase PWM rectifier with sliding-mode control
仿真结果对比分析如下:
图4所示分别是采用PI控制和滑模控制的相电压和相电流的仿真波形。可以看到,采用PI控制的A相电流在0.03 s左右实现了与电压同相,即对电压相位的跟随,而采用滑模控制的A相电流在0.02 s左右就实现了对电压相位的跟随,保持单位功率运行,且波形良好,正弦度高。
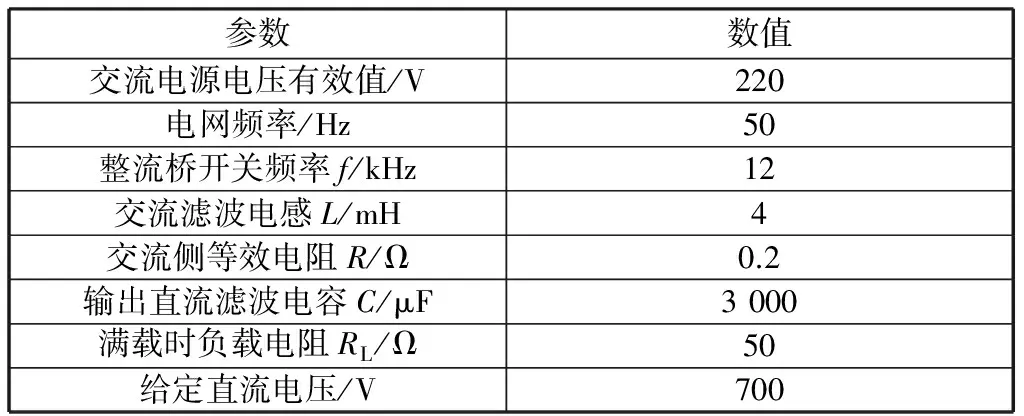
表1 三相PWM整流器参数表Table 1 Parameters Table of Three-phase PWM rectifier
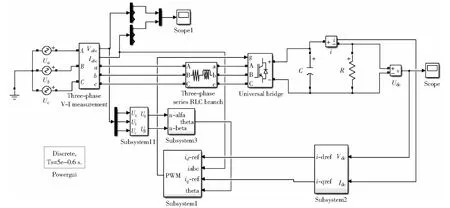
图3 滑模控制三相PWM整流器系统模型Fig.3 System mode of three-phase PWM rectifier with sliding-mode control
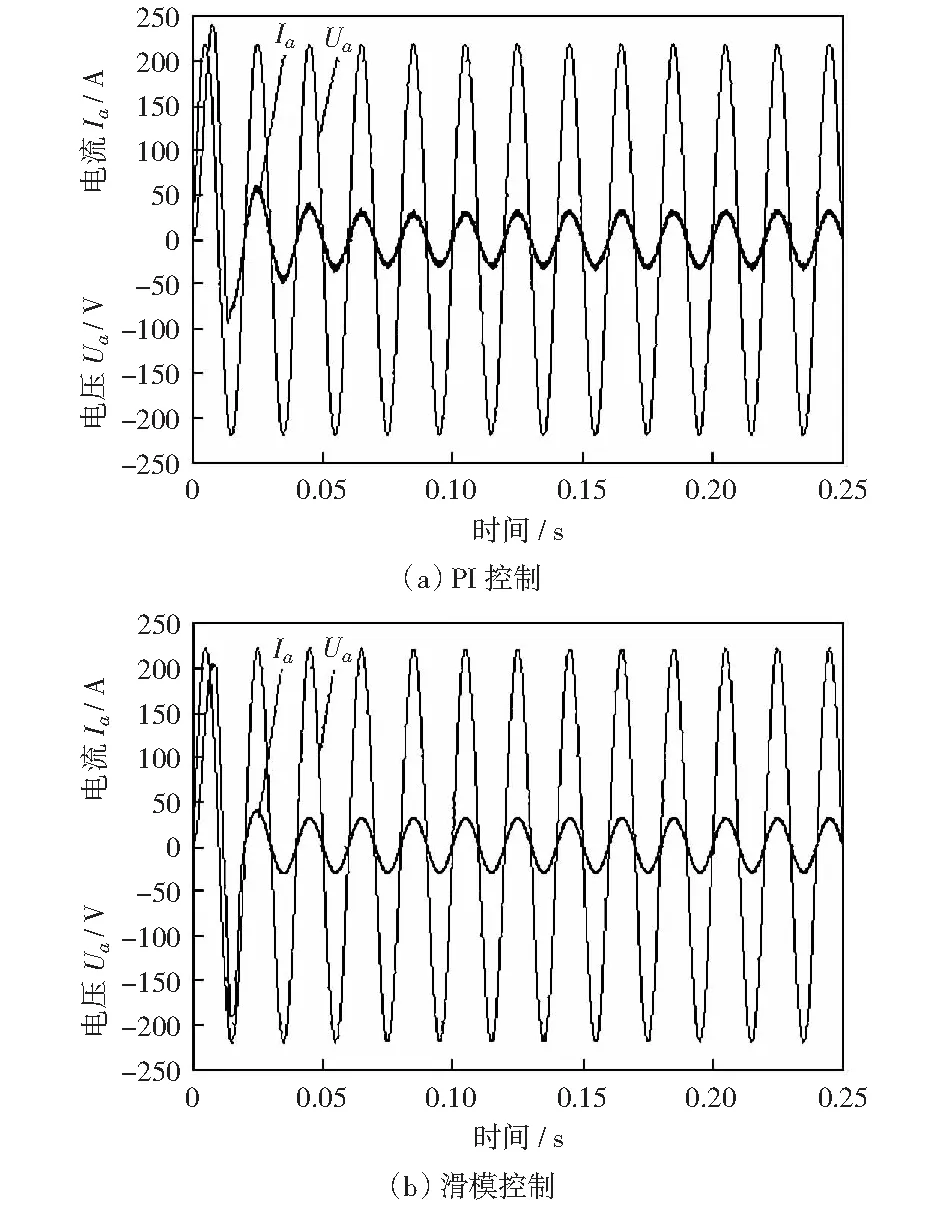
图4 网侧A相电压电流波形Fig.4 Waveforms of A phase voltage and current

图5 直流侧输出电压波形Fig.5 Waveform of the DC voltage
图5是输出直流电压的波形对比。其中,图5(a)是采用PI控制的输出直流电压波形,图5(b)是采用滑模控制的输出直流电压波形。可以看到2种控制模式下的输出直流电压都在很短的时间内实现了较快的动态响应,在采用PI控制的整流器控制系统中,输出直流电压的波形在0.13 s之后达到稳定并保持在给定的参考电压值700 V;而在采用滑模控制的系统中,输出直流电压波形在0.03 s左右就达到稳定并保持在给定的参考电压值700 V,且超调量很小。
为了进一步展示本控制系统的动态性能,又对给定直流电压突变情况下的整流器进行了对比仿真实验。如图6和图7所示,在0.15 s给定直流电压由700 V突增到800 V时的响应波形。图6为采用PI控制的整流系统的响应波形图,图7为采用滑模控制的整流系统的响应波形图。

图6 PI控制系统在给定直流电压由700 V变为800 V时动态响应波形Fig.6 Dynamic response of the given-voltage change from 700 V to 800 V with PI-mode control

图7 滑模控制系统在给定直流电压由700 V变为800 V时动态响应波形Fig.7 Dynamic response of the given-voltage change from 700 V to 800 V with sliding-mode control
由图6可以看到,采用PI控制的系统在大约0.25 s时达到稳定;在图7中采用滑模控制的系统0.17 s就达到了稳定状态。比较分析基于PI控制的整流系统动态响应波形和采用滑模控制的整流系统的动态响应波形,可以看出,采用滑模控制的整流系统直流输出电压在出现扰动的情况下波动更小,系统恢复到稳态所需要的时间更短,从而证明运用滑模控制的PWM整流器具有更好的动态性能和鲁棒性。
5 结论
提出了一种新的三相PWM整流器的控制策略,即电压外环和电流内环全部采用滑模控制的控制方案,较之于采用PI控制的整流系统,动态性能和鲁棒性都得到了明显的改善和提高。最后,在Matlab/Simulink中的仿真结果表明所提控制系统启动时间短、网测电流波形好、输出直流电压稳定且无超调,证明该控制方案比采用PI控制的整流方案有着更高的理论价值与应用价值。
[1] 贾宇辉,李剑林,王孝洪,等.PWM整流器滑模变结构控制算法研究[J].电测与仪表,2011,48(7):7-10.
JIA Y H,LI J L,WANG X H,et al.Study on sliding-mode variable structure control algorithm for PWM rectifier[J].Electrical Measurement & Instrumentation,2011,48(7):7-10.
[2] 唐勇奇,赵葵银,汪超.基于滑模变结构控制的三相PWM整流器[J].电力自动化设备,2006,26(5) :39-41.
TANG Y Q,ZHAO K Y,WANG C.Three-phase PWM rectifier based on sliding-mode variable structure control[J].Electric Power Automation Equipment,2006,26(5):39-41.
[3] 彭一芯.三相电压型PWM整流器PID神经网络滑模控制研究[D].湘潭:湘潭大学,2015.
[4] 周莹.模糊滑模变结构控制策略在PWM整流器系统中的运用[J].水电能源科学,2015,33(8):174-177.
ZHOU Y.Research of PWM rectifier control system based on fuzzy sliding mode control strategy[J].Water Resources and Power,2015,33(8):174-177.
[5] 张崇巍,张兴.PWM整流器及其控制[M].北京:机械工业出版社,2003.
[6] SILVA F J.Sliding-mode control of boost-type unity-power-factor PWM rectifiers[J].IEEE Tran Industry Electronics,1999,46(3):594-603.
[7] 王长恺,尹华杰.三相电压型PWM整流器的系统设计与PI参数校正[J].电气传动,2011,41(3):41-45.
WANG C K,YIN H J.System design and PI parameter calibration of three-phase voltage source PWM rectifier[J].Electric Drive,2011,41(3):41-45.
[8] 刘金棍.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005.
[9] KALE M,OZDEMIR E.An adaptive hysteresis band current controller for shunt active power filter[J].Electric Power Systems Research,2005,73(2):113-119.

