基于矫顽力的钢板应力检测技术
,,, ,
(沈阳工业大学 信息科学与工程学院,沈阳 110870)
钢板被广泛应用于工业生产制造及建筑领域,其在投产服役的过程中会产生应力集中区域,从而出现裂纹等缺陷。对钢板所受应力的检测方法包括超声检测法、X射线检测法及磁性法等多种检测方法[1]。
磁性法是通过测量铁磁性材料磁性参数,如磁导率、磁阻及矫顽力等来对材料应力进行检测的方法。常见的磁性检测方法包括金属磁记忆法、磁致伸缩法及巴克豪森效应法等[2]。在各磁性参数中,矫顽力与应力存在一定的关系,且其测量不易受外界干扰,利用矫顽力实现对钢板所受应力的检测具有较好的应用价值[3]。
笔者通过测量钢板矫顽力实现对其所受应力的检测,建立了矫顽力与应力的线性关系模型,对不同型号钢板试件的矫顽力及其所受应力进行了检测数据采集及拟合。试验结果表明:钢板矫顽力与所受应力间存在线性关系,利用线性关系可以对钢板所受应力进行检测与分析。
1 基于矫顽力的应力检测机理
1.1 铁磁性材料磁化过程及其对矫顽力的影响
铁磁性材料的内部可分为若干小区域,这些区域称为磁畴,每一个磁畴的磁矩方向各异,相邻磁畴分界处称为畴壁[4]。
铁磁性材料在外界磁场的作用下,材料逐渐被磁化最终达到磁饱和,磁化过程中会发生畴壁位移和磁畴转动。该过程可用曲线来表示,铁磁性材料磁化过程分成4个磁化阶段,Ⅰ阶段为可逆畴壁位移阶段,Ⅱ阶段为不可逆畴壁位移阶段,Ⅲ阶段为可逆磁畴转动阶段,Ⅳ阶段为趋近饱和阶段。铁磁性材料的磁化过程如图1所示。

图1 铁磁性材料的磁化过程示意
在磁化过程的第Ⅱ阶段中,磁化强度会随着外磁场的增加而快速增加,磁畴结构重新组合,畴壁发生跳跃式移动,这种位移属于不可逆移动变化,无法得到恢复。
矫顽力与磁化过程的第Ⅱ阶段有关,该阶段导致了畴壁的移动,畴壁之间出现接触挤压。当撤去外磁场时,无法恢复到未磁化状态,形成磁滞。磁滞影响了磁滞回线的面积,而导致矫顽力的变化[5]。
1.2 矫顽力与应力的线性关系模型
从能量的角度分析,畴壁的位移需要能量的积累,而导致能量增加的因素有很多,其中应力是导致能量增加的主要原因之一。能量积累到达一定程度时会引起畴壁的位移[6],影响材料的矫顽力。
应力导致不可逆畴壁位移的H0临界场如式(1)所示。
(1)
式中:Ms为饱和磁化强度;μ0为真空磁导率;θ为畴壁位移后磁矩和磁场方向的夹角;γ为单位面积的畴壁能;x为畴壁的相对位置。
最大临界场H0max如式(2)所示。
(2)
畴壁能的表达式为
(3)
式中:λs为磁致伸缩系数;A为交换积分;K1为能量密度;σ(x)为应力随畴壁位置变化的函数;δ为应力存在时畴壁的基本厚度。
对x微分得
(4)
式(4)中δ可表示为
(5)
根据不同的材料,应力的分布按应力波长l与畴壁厚度δ的大小关系进行区分,分为畴壁厚度远小于应力波长和畴壁厚度远大于应力波长两种情况,如图2,3所示。
(1) 畴壁厚度远小于应力波长,即δ≪l时,应力分布如图2所示,畴壁内部的应力可用常数进行表示。

图2 δ≪l时应力分布示意
由图2可知
(6)
式中:Δσ为应力最大变化量。
由于δ≪l,δ可看做常数,对γ求微分得到
(7)
将式(7)代入式(1),得到临界场为
(8)
(2) 畴壁厚度远大于应力波,即δ≫l时,应力分布如图3所示。

图3 δ≫l时应力分布示意
当畴壁移动到应力不均衡处时(x=x1),由于畴壁远大于应力不均匀的范围(δ≫l),需要考虑应力能,故畴壁能需要添加Δγσ,计算式为
(9)
由图3可知,可将式(9)的积分简化为
(10)
当x=0.329δ时,Δγσ对x的微分取得最大值,其值为
(11)
将式(11)代入到式(1)可得临界场为
(12)
式(8)及式(12)的临界场公式统一归纳为
(13)

(14)
各临界场的平均值,即应力影响下的矫顽力Hc的表达式为
(15)
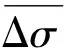

2 矫顽力检测系统
2.1 矫顽力检测原理
矫顽力检测系统可以对检测区域内材料的矫顽力进行测量,通过测量被测试件的矫顽力实现对应力集中区域的检测。
系统选用结构简单的U型传感器作为检测传感器。在激励端产生激励信号输入至激励线圈,在检测传感器与被测试件构成的闭合回路中产生磁场,其磁场强度由激励信号的电流决定。由电磁感应定律可知,激励电流发生变化时,磁通量发生改变,进而导致检测线圈感应电动势发生改变,磁感应强度也发生变化[7]。矫顽力检测原理如图4所示。
图4 矫顽力检测原理示意
在测量回路中,假设没有漏磁,磁路方程为
NI=HsLs+HyLy
(16)
式中:N为激励线圈的匝数;I为激励端的激励电流;Hs为被测试件磁场强度;Hy为检测传感器的磁场强度;Ls为被测试件磁路长度;Ly为检测传感器的磁路长度。
Hs可用H近似替代
(17)
感应线圈中感应磁通量φ为
φ=BS
(18)
式中:B为磁感应强度;S为磁路截面面积。
故可得磁感应强度B的计算式为
(19)
式中:n为感应线圈匝数;U感为感应线圈感应电压。
由矫顽力的定义可知,当磁感应强度等于0时,磁场强度H即当前被测试件矫顽力的值。
2.2 矫顽力检测系统组成
矫顽力检测系统分为3部分:信号发生及功率放大电路、感应信号调理电路和A/D采集电路。矫顽力检测系统原理如图5所示。

图5 矫顽力检测系统原理示意
在磁芯上绕制激励线圈和感应线圈,由信号发生电路产生5~200 Hz的正弦信号,信号经过功率放大电路输入至激励线圈两端,对检测传感器及被测试件进行磁化,构成闭合磁回路并产生激励磁场。磁场在感应线圈两端产生感应信号,经过感应信号调理电路提取过零点。检测过零点时刻激励端的电流,由式(17)计算可得到矫顽力。系统各部分的具体实现流程如下所述。
(1) 信号发生及功率放大电路
信号发生及功率放大电路包括信号发生电路及功率放大电路两部分。信号发生电路采用AD9850芯片产生幅值为1 V,频率为10~200 Hz的连续可调正弦信号。在此频率范围内找到最适合的磁化频率。信号发生电路示意如图6所示。

图6 信号发生电路示意
功率放大电路采用功率放大芯片进行信号功率的加强,其产生30 W的大功率激励信号来对检测传感器及被测试件进行磁化,使磁化强度满足检测标准。功率放大电路示意如图7所示。
图7 功率放大电路示意
(2) 感应信号调理电路
感应信号调理电路由积分电路和过零检测电路组成。感应线圈感应到的电磁信号通过积分电路进行积分运算,积分后的信号经过光电耦合芯片组成过零检测电路,提取信号过零点。最后将过零脉冲信号送给微处理器进行中断处理。
(3) A/D采集电路
为得到矫顽力随应力的变化关系,需要将应力作用下包含矫顽力的磁信号检出。采集激励端的采样电阻两端的电压,经过16位A/D转换芯片LTC1864将电压进行模数转换,通过SPI(串行外设接口)的传输方式输入至微处理器。A/D采集电路示意如图8所示。
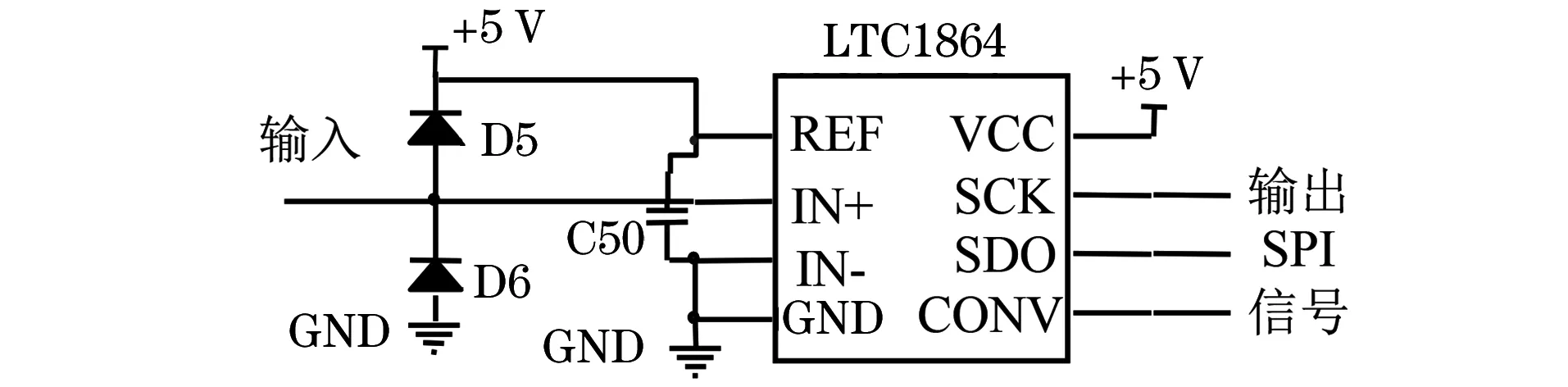
图8 A/D采集电路示意
2.3 测量数据拟合方法
为了分析铁磁性材料矫顽力与应力间的关系及趋势,需要对试验数据进行拟合。采用最小二乘法作为数据拟合方法。
设铁磁性材料检测得到的矫顽力数值为x1,x2,…,xn,对应的铁磁性材料所受应力大小为y1,y2,…,yn,拟合函数为
y(x)=ax+b
(20)
矫顽力与应力数据的离散点到拟合曲线的平方和为
(21)
对式(21)中的a与b求偏导数,整理得到方程组
(22)
通过求解方程组(22)可以得到a和b的拟合参数。将拟合参数代入式(20)可得到铁磁性材料矫顽力与所受应力的拟合曲线。
3 试验过程与结果分析
试验选用Q235、X70及X80型号钢板进行拉伸试验,钢板试件采用板状标准试件结构,具体结构示意如图9所示。

图9 钢板试件结构示意
将6 mm厚度不同型号的钢板试件放于计算机控制的万能材料试验机上进行拉伸,将检测传感器置于试件的拉伸段处,在弹性阶段对试件进行拉伸,记录钢板试件矫顽力与试验机拉力的数值。根据试验数值进行最小二乘曲线拟合,分析变化趋势。拉伸试验系统示意如图10所示。

图10 拉伸试验系统示意
钢板在材料试验机上所受到的应力大小可由式(23)计算得出
σ=F/S
(23)
式中:σ为铁磁性材料所受到的应力;F为铁磁性材料受到的拉力;S为铁磁性材料的横截面积。
根据式(23)可以将试验机拉力转化为试件所受到的应力。得到不同型号钢板试件拉伸试验数据如表1所示。

表1 不同型号钢板试件拉伸试验数据
根据式(20)分别建立各型号钢板检测矫顽力与应力的拟合函数,将表中各型号钢板的矫顽力及对应的应力分别代入式(21)求平方和,通过式(22)分别对拟合参数求偏导解出最小二乘拟合参数a和b,最终得到Q235、X70及X80钢板试件矫顽力与所受应力间的最小二乘拟合函数表达式分别为
yQ235(x)=1.345xQ235-1 275.243
(24)
yX70(x)=1.284xX70-1 137.458
(25)
yX80(x)=5.067xX80-4 954.276
(26)
根据式(24),(25)及(26)得到不同钢板拉伸试验数值曲线及最小二乘拟合曲线如图11所示。
由图11可知,不同型号钢板试件的矫顽力与所受应力均呈线性变化,试验结果与理论分析结果一致,由于钢板矫顽力受磁致伸缩系数、饱和磁化强度等磁性参数的影响,不同型号钢板矫顽力数值的大小及曲线的变化率有所不同。

图11 不同型号钢板拉伸试验数值曲线及最小二乘拟合曲线
4 结论
(1) 应力会使作用区域内能量增加,进而影响磁畴运动,导致矫顽力变化,理论与试验结果表明,钢板的矫顽力与所受应力之间呈线性变化。
(2) 不同钢板材料的线性变化率因材料的磁致伸缩系数、饱和磁化强度等参数的不同而不同。
(3) 根据矫顽力与所受应力的线性变化规律,可以通过测量钢板的矫顽力对钢板所受应力进行检测与分析。
[1] 杨理践,张良,高松巍.基于矫顽力的铁磁性材料应力检测技术[J].无损检测,2014,36(12):65-68,72.
[2] 沈功田,郑阳,蒋政培,等.磁巴克豪森噪声技术的发展现状[J].无损检测,2016,38(7):66-74.
[3] 郭子政,胡旭波.应力对铁磁薄膜磁滞损耗和矫顽力的影响[J].物理学报,2013,62(5):420-425.
[4] 张志东.磁性材料的磁结构、磁畴结构和拓扑磁结构[J].物理学报,2015,64(6):5-21.
[5] 任尚坤,周莉,付任珍.铁磁试件应力磁化过程中的磁化反转效应[J].钢铁研究学报,2010,22(12):48-52.
[6] STUPAKOV O,TOMAS I.Optimization of single-yoke magnetic testing by surface fields measurement [J].Journal of Physics D Applied Physics,2006,39(2):248-254.
[7] 罗新,吴伟,李大鹏,等.20CrMnTi钢渗碳淬火硬化层深度的磁矫顽力检测[J].无损检测,2016,38(7):47-50.

