凯威特单层球面网壳稳定性分析初始几何缺陷最大计算值的合理选取

王 炜 雷庆关

（安徽建筑大学）

1 初始几何缺陷分布模拟问题

在实际工程设计中，关于初始几何缺陷的选取问题，工程人员一般会放大保守系数进行网壳设计，来确保壳体的稳定极限承载力有一定的安全范围保障。在初始几何缺陷的分布模态中，随机缺陷模态的分布主要考虑的是多维随机变量问题，因为在它的样本空间中，每一个样本点代表了一种缺陷模态。所以，在随机缺陷模态中，初始安装就是一个随机变量。这种方法可以切实的反应出现实结构的受力状态，但是计算任务量比较大。而一致缺陷模态分步法则采用网壳最低阶的屈曲模态来进行模拟网壳的初始几何缺陷分布。本文将采用一致缺陷模态法对网壳结构的稳定极限承载力开展分析研讨工作。

2 初始几何缺陷最大计算值合理选取的分析

2.1 算例

本章以实际工程中常用的跨度40m、50m、60m，矢跨比分别为1/7、1/6、1/5、的三向网格型、K8型、联方型3种经常采用的网壳结构为研究对象，来进行上述模型结构的分析工作，并对初始几何缺陷的选取进行探讨。分别对网壳考虑了 L/1000、L/500、L/300、L/150、L/100，依次有五类不同的初始几何缺陷与不考虑初始几何缺陷的完善网壳结构，对不同的初始几何缺陷进行分析计算并对比得出结论，各计算模型的计算简图如图1所示。上述模型的具体参数见表1。

图1 三种模型结构图

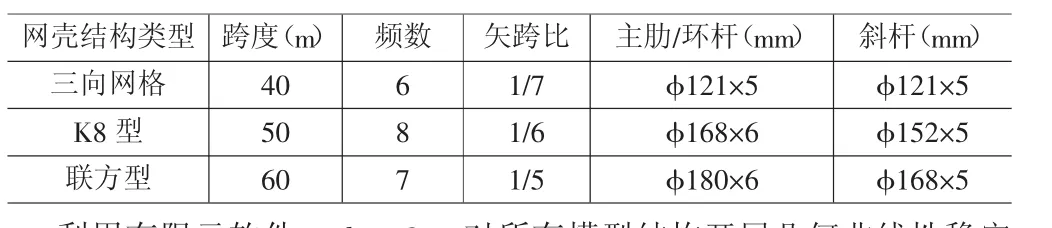
表1 各模型计算参数表

利用有限元软件midas-Gen对所有模型结构开展几何非线性稳定分析工作，仅分析几何非线性。钢材的弹性模量可取为206×103N/mm2，屈服强度为235N/mm2，质量密度取7850kg/m3，泊松比可取值为0.3。支座全部采用铰支座，永久荷载取值0.5KN/m2，壳面可变荷载均匀布置于整跨，取值 0.5kN/m2。

2.2 计算分析

缺陷大小分析对比

采用一致缺陷模态法对图1中三个典型结构模型开展非线性稳定性分析工作，初始几何缺陷最大值分别取 0、1/1000、1/500、1/300、1/200、1/150、1/100七种情况，首先对理想壳进行稳定极限承载力分析，求得稳定极限承载力，分别对各个系统结构施加以上七中不同的初始几何缺陷，并求解它们在七中不同缺陷值下的缺陷影响系数。计算结果见表2所示。

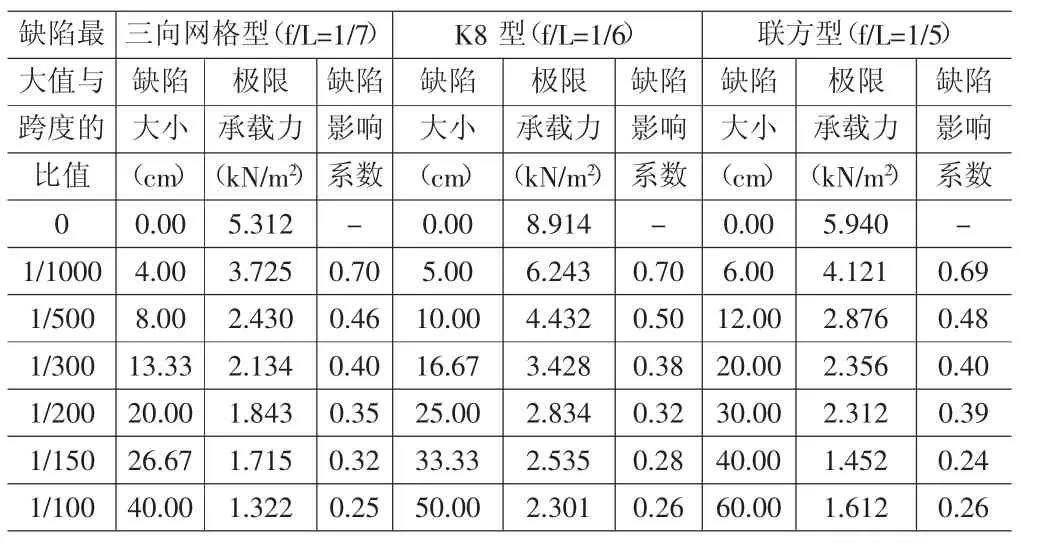
表2 3个典型模型采用不同初始几何缺陷最大值计算结果表

分析中，考虑双重非线性进行网壳分析，此时结构的计算稳定承载力也随之发生了很大变化，随着初始几何缺陷增大，呈现先下降后上升的现象，在此分析中还发现，若缺陷值取“网壳跨度的1/300”，此时网壳的稳定极限承载力最小。则表明，同样的考虑双重非线性条件下，此时结构的计算稳定承载力也随之发生了很大变化，随着初始几何缺陷增大，呈现先下降然后逐渐变平缓的现象，也可能出现一直下降的现象。文献[2]证实了关于缺陷网壳的另一种界说，文中提出了有缺陷的的实际网壳结构的极限承载力为理想网壳极限承载力的50%。提出了缺陷影响值系数，用来分析几何缺陷对网壳结构稳定极限承载力的影响大小，并确定在初始几何缺陷取值为网壳跨度的1/300时，缺陷影响值系数取0.5较为合适。同样，也提出了有缺陷的的实际网壳结构的极限承载力为理想网壳极限承载力的50%。

总得来说，初始几何缺陷值在按照网壳结构跨度的1/300取值时，此时根据上述表中可知，缺陷影响系数在0.42左右，此时对结构设计来说偏向保守，而当缺陷影响系数取值为0.5时，可以看出，初始几何缺陷对壳体的稳定极限承载力影响已经充分体现出来，也比较合理。因此本文建议在后续进行单层网壳球面稳定分析时，初始几何缺陷的最大值取值为网壳跨度的1/500。

2.3 本章小结

本章选用一致缺陷模态法，对三向网格型、K8型、联方型3种单层网壳进行了荷载-位移全过程分析。在此基础上，对网壳结构开展稳定性分析工作，并对初始几何缺陷最大计算值的合理选取实行了剖析讨论。主要结论如下：

（1）当缺陷影响系数取值为0.5时，可以看出，初始几何缺陷对壳体的稳定极限承载力的影响已经充分体现出来。

（2）初始几何缺陷和稳定极限承载力之间存在一定的规律，若初始几何缺陷最大值不断增大，壳体的稳定极限承载力呈现出逐渐降低的趋势，整个壳体的受力性质发生了改变，一开始是薄膜内力为主，之后转化为不以薄膜内力为主。而当网壳结构初始几何缺陷最大值取为网壳结构跨度的1/300，壳体的受力状况也发生更改，同样不在以薄膜内力为主。

（3）初始几何缺陷为1/500时，它所对应的各个模型，其中轴向力杆件居多，大约为73%，所对应的弯曲内力比均值为0.24，因此可以看出此时的壳体已经不再以薄膜内力为主了，此时可判定壳体是以受薄膜内力为主的受力状况。

（4）单层球面网壳结构稳定分析时，在考虑初始几何缺陷的时候，不论是网壳的施工验收，还是受力状态来考虑，综合分析，建议在进行非线性稳定分析时初始几何缺陷取值为网壳跨度的1/500较为合理。

[1]Shiro Kato，Jong-ming Kim，Yutaka Niho.Propotioning Method for Member Sections of Single Layer Reticulated Domes Based on the Results of Liner Buckling Analysis[J].2000：25～40.

[2]曹正罡，范峰，沈世钊.K6型单层球面网壳的弹塑性稳定[J].空间结构，2005（03）：22～26.

[3]张毅刚.大跨空间结构[Z].北京：机械工业出版社，2012，153～192.

[4]曹正罡.网壳结构弹塑性稳定性能研究[D].哈尔滨工业大学，2007.

[5]郭海山，钱宏亮，沈世钊.地震作用下单层球面网壳结构的动力稳定性[J].地震工程与工程振动，2003（01）：31～37.

[6]范峰，严佳川，曹正罡.考虑杆件失稳影响的网壳结构稳定性研究[J].土木工程学报，2012，45（5）：8～17.