空间站舱体转位试验系统动力学匹配设计与仿真

胡雪平，时军委，沈晓鹏，刘 艳

（上海市空间飞行器机构重点试验室，上海宇航系统工程研究所，上海201108）

1 引言

中国载人航天工程计划在2020年前后建成和运营近地空间站，规划中的中国空间站包括核心舱、实验舱 I、实验舱 II，基本构型如图 1所示［1⁃2］。 实验舱 I、II 通过转位机构由轴向对接口转至实验舱侧向对接口，为后来的对接让出轴向对接通道。中国空间站组建用的转位机构采用平面转位方案［1］，即实验舱在整个转位过程中在平面内运动，过程中核心舱处于无控状态。

图1 中国空间站基本构型［1］Fig．1 Basic configuration ofChinses space station［1］

转位机构如图2所示，其转位功能由位于实验舱的转臂和位于核心舱的基座两部分配合实现，基座固连在节点舱（核心舱）上，通过腕关节实现核心舱与臂杆相对转动，支架固连在实验舱上，通过肩关节实现实验舱与臂杆相对转动［1］。

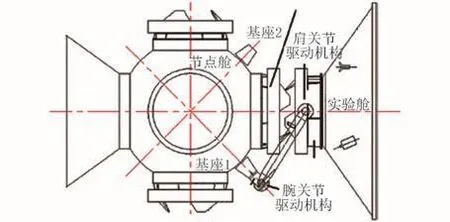
图2 转位机构布局［1］Fig．2 Layout of transfer mechanism［1］

转位过程是关乎空间站组建成败的关键环节之一，在轨转位过程中，核心舱处于停控状态，核心舱和实验舱相对转动，同时又整体运动。如果在地面进行与在轨同状态的转位过程试验，我们认识到地面需要具备以下条件：1）核心舱和实验舱的质量为实际质量；2）试验场地足够大，可以满足核心舱和实验舱转位前后的运动包络。实际上，地面试验由于场地大小和承载限制，同时考虑安全性要求，无法像空间一样使两舱均处于漂浮状态。因转位过程是实验舱从轴向口转位至侧向口，将核心舱通过基体固定，实验舱随转臂转动［1］，与空间转位状态存在差异。为了能考核转臂双关节在轨状态的运动特性，需要等效模拟惯量和质量，等效原则为关节在转位过程中的运动参数和动力学效果一致。

在地面进行试验时，为了能够考核转位机构弹簧阻尼机构关节的启动和制动特性，需要模拟在轨的失重环境。试验方案上由于核心舱固定，实验舱转动，因此需要对实验舱的重量进行平衡。

在地面进行失重状态模拟试验，目前比较常用的模拟方法有悬挂法、气浮法和和水浮法［3⁃4］。悬挂方法存在很多外加干扰，精度有限；气浮式系统精度高，但只能提供两维空间运动；水浮法维护费用较高，对系统的防水性具有很高要求，国内应用较少。地面试验系统惯量模拟通常物理惯量或电惯量模拟［5⁃6］。使用物理惯量是传统的模拟方法，以能量等效为基础进行，模拟真实，无控制难度，大惯量和大质量的模拟成本较高。电惯量模拟近年兴起，通过控制电动机的转速或电磁力矩实现惯量模拟，具有结构简洁、惯量连续和可进行误差补偿等诸多优点；但如果动力学系统复杂则控制难度加大，模拟的准确性难以保证，且受电机能力的限制，一般模拟的惯量和质量不大。

转位机构的转位惯量和质量均很大，同时转位过程通过肩关节和腕关节交替运动实现，肩关节和腕关节存在动力学耦合现象，采用电惯量模拟难度大，真实性不够，因此适合采用物理惯量来进行模拟。中国空间站组建用的转位机构采用平面转位方案［1］，转位过程地面试验中，考虑精度需要，转位机构双关节特性试验采用气浮法更为合适。由于气浮试验受制于两维空间运动，因此必然涉及二维平面模拟空间三维动力学特性的等效性［5⁃6］。

在气浮法模拟舱体失重环境条件下，使用双关节特性试验装置，如果带动与实际舱体质量惯量相同的负载，对于相同的关节而言，与在轨的动力学特性是不匹配的，须针对二维平面模拟空间三维动力学特性的等效性问题进行地面双关节试验系统的质量特性匹配设计。

Syromiatniko［7］通过欧拉动力学方程结合约束方程的方法求解了转动关节的转角，但未结合试验系统进行模拟器的质量参数设计。徐志刚等［8］通过拉格朗日方法建立了惯量模拟器等效负载数学模型，但其惯量模拟器是差动轮系增速机构。本文针对真实的转臂、肩关节、腕关节机构连接物理的实验舱模拟器模拟在轨舱体转位过程的地面转位模拟试验系统，通过拉格朗日第二动力学方法，建立在轨与地面试验系统之间的等效动力学关系，给出物理的实验舱模拟器的质量、惯量、以及质心位置，为双关节试验系统研制提供依据。

2 实验舱模拟器的质量特性匹配设计与分析

在轨转位动力学系统由核心舱、实验舱、转臂三个运动刚体组成，实验舱和转臂之间通过肩关节连接，是一种转动副约束，节点舱和转臂之间通过腕关节连接，是转动副约束。根据机械原理中自由度计算公式，三个运动刚体、两个转动副约束的系统具有八个自由度，地面双关节试验系统中，节点舱模拟器固定在大地，实验舱模拟器和转臂是两个运动刚体、实验舱模拟器和转臂由肩关节连接，转臂和节点舱模拟器即基体由腕关节连接，根据机械原理中自由度的计算公式，两个运动刚体、两个转动副约束的系统具有两个自由度［9］。

2.1 匹配需求问题

在轨转位运动中，节点舱（核心舱）和实验舱与转臂以转动关节约束，并作用有偏转弹簧阻尼机构，舱体本身自由停控。在轨转位原理可简化为图3所示模型，对应的地面双关节试验系统可简化为图4所示模型。

图3 在轨转位原理Fig．3 Principle of on⁃orbit transfer process

用两个自由度的地面试验系统模拟在轨八个自由度的动力学过程，为保证有效性，地面试验系统中质量惯量模拟器的质量特性（实验舱和核心舱等效到肩关节的等效质量、质心位置，包括质量块的主要尺寸等）需要进行设计试验。设计需要的输入参数包括在轨实验舱、核心舱、转臂质量、惯量和质心位置以及关节的弹簧特性，见表1。

2.2 三体三维模型到平面模型的分析

在关节性能输入相同的情况下，匹配性设计的思路是三体三维模型简化为三体平面模型，即在模型和关节的性能输入相同的情况下，对核心舱施加平面约束，强制核心舱只做平面运动，消去核心舱的三个自由度。假设合理性可通过Adams仿真验证，其中腕关节和肩关节的电机驱动角速度仿真曲线见图5，关节驱动曲线主要分为启动段、平稳运行段、制动段。三体模型的空间运动与平面运动的肩关节和腕关节弹簧阻尼力对比结果分别见图 6、7。

图5 关节电机驱动角速度Fig．5 Angular speed of joints by motor drive

图6 肩关节弹簧阻尼力对比曲线Fig．6 Comparison of spring damping force in shoul⁃der joint

由对比结果可知，三维运动简化为平面运动，主要的运动趋势特征保留下来，最大误差约6%，说明空间三体运动假设为平面运动是合理的。

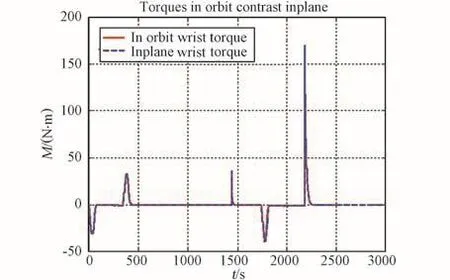
图7 腕关节弹簧阻尼力对比曲线Fig．7 Comparison of spring damping force in wrist joint

类似地，在模型、关节性能输入相同的情况下，匹配性设计的第二步假设是三体平面模型可简化为两体平面模型，对于核心舱施加固定约束，消去核心舱的六个自由度，使简化后的系统只有两个关节的自由度。对比核心舱自由和固定状态两种状态下的肩关节和腕关节弹簧阻尼力，未经质量匹配的两体模型两维运动Adams仿真结果与三体模型的空间运动（如图8～9）差异很大，说明核心舱在固定状态下，直接用实验舱在轨的质量惯量，关节弹簧阻尼力远大于在轨系统，要想得到关节弹簧阻尼力与在轨类似的系统，需要调整试验用的实验舱质量惯量。

图8 肩关节弹簧阻尼力对比曲线Fig．8 Comparison of spring damping force in shoul⁃der joint

3 平面模型质量特性匹配设计

3.1 三体平面动力学模型

由2.2节的简化分析可知，在核心舱停控条件下，在轨转位实验舱动力学过程简化为三体平面动

图9 腕关节弹簧阻尼力对比曲线Fig．9 Comparison of spring damping force in wrist joint

力学模型是合理的。建立的动力学模型如图10。

图10 转位过程简图Fig．10 Sketch of on⁃orbit transfer process

其中， R1、R0、R2分别表示核心舱、转臂、实验舱质心相对绝对坐标系的矢量，r1、r0、r2表示腕关节中心相对核心舱质心的矢量、臂杆杆矢量（即肩关节中心相对腕关节中心的矢量）和实验舱质心相对肩关节中心矢量，o1x1y1、o0x0y0、o2x2y2表示核心舱、转臂、实验舱质心坐标系，oxy表示绝对坐标系。以转臂质心在平面上的坐标（x0，y0，θ0）和肩关节、腕关节两个关节角α、β为未知数，关节角是转臂与核心舱或实验舱之间的相对转角，通过第二类拉格朗日方程建立动力学方程。其中刚体位置间的运动约束关系如式（1），由于臂杆的质量远远小于舱体而忽略了臂杆能量的拉格朗日函数如式（2），三体二维动力学方程见式（3）。 式中 x1、y1、θ1是核心舱质心在平面上的坐标以及转臂在平面内的绝对转角，x2、y2、θ2是实验舱质心在平面上的坐标以及转臂在平面内的绝对转角。

3.2 两体平面动力学数学模型

地面试验系统是两体平面动力学模型，运动可简化为图11，其中r1s表示实验舱模拟器质心相对肩关节中心矢量，o1sx1sy1s表示实验舱模拟器质心坐标系。

图11 地面转位过程简图Fig．11 Sketch of ground transfer process

在不影响结果的前提下，为了简化模型，可以将腕关节相对转角α与转臂相对基体的绝对转角θ0取为相同。建立两体位置约束方程如式（4），两体平面动力学方程如式（5）。

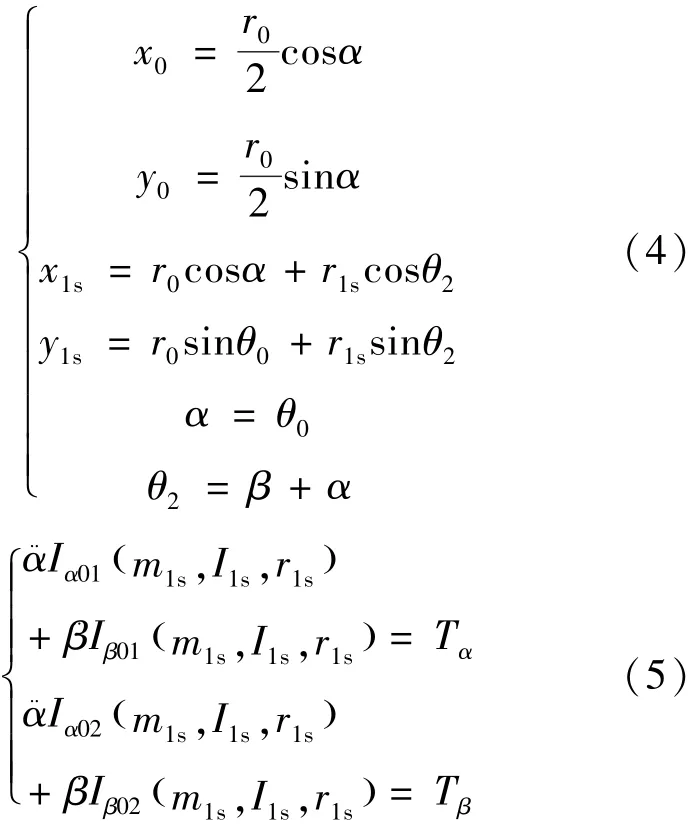
其中m1s、I1s是实验舱模拟器的质量和惯量。通过（3）和（5）的相等，通过 Matlab编程计算得m1s＝2000 kg，I1s＝3.5 ×105kg·m2。

3.3 实验舱模拟器质量特性分析

假设试验使用图12所示均质立方体物块，a是立方体边长一半，外表面与轴距离是L。基于两体平面所得的等效惯量，匹配得到L＝8 m、7 m、6 m、5 m时与质量块边长的对应关系见图13及表2。

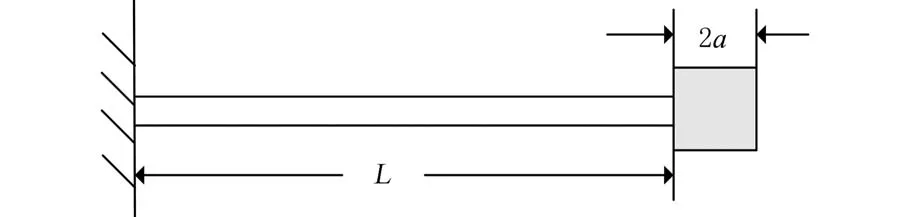
图12 试验质量块Fig．12 Mass block of experiment

图13 质量块杆长与质量块边长关系Fig．13 Rod length and side length of mass block

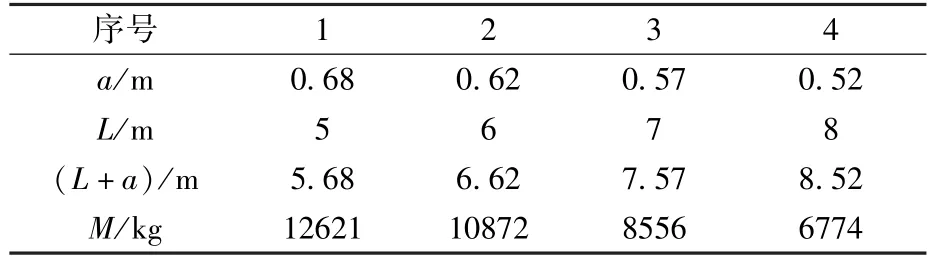
表2 质量块有效杆长及边长Table 2 Effective rod length and side length of mass block

4 仿真校验

以连杆长度L＝8.5 m情况作为试验系统仿真输入，进行试验系统和在轨转位仿真对比，试验系统和在轨动力学的关节参数输入和驱动参数输入相同，仿真结果见图14～15。

图14 肩关节的力矩曲线Fig．14 Torque curve in shoulder joint

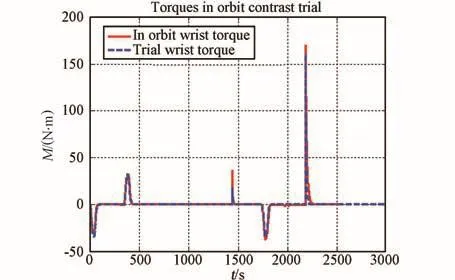
图15 腕关节的力矩曲线Fig．15 Torque curve in wrist joint

在轨动力学与试验系统动力学的力矩曲线在趋势上非常相似，接近程度最大误差约7%，仿真结果说明：通过本文的分析方法所给的试验所用实验舱的质量特性有效，明确地为双关节试验系统的质量块质量特性提供了研制依据。

5 结论

本文针对地面双关节测试系统模拟在轨核心舱无控状态下转位机构转位实验舱的动力学过程。针对这两个动力学过程，建立了转位机构关节动力学特性等效关系式，设计出测试系统中应该使用的实验舱模拟器质量、惯量、质心位置等。试验系统动力学与在轨动力学的仿真对比显示，接近程度最大误差约7%，证明了设计结果有效。

（

）

［1］ 沈晓鹏，刘艳，胡雪平.空间站转位组建方案研究［J］.载人航天， 2015， 21（5）：450⁃467.Shen Xiaopeng， Liu Yan，Hu Xueping.Study on transfer con⁃struction scheme of space station ［ J］.Manned Spaceflight，2015， 21（5）：450⁃467.（in Chinese）

［2］ 周建平.我国空间站工程总体构想［J］.载人航天，2013，19（2）：1⁃10.Zhou Jianping.Chinese space station project overall vision［J］.Manned Spaceflight，2013，19（2）：1⁃10.（in Chinese）

［3］ 曾磊，孙鹏飞，陈明.空间机械臂水下试验及其关键技术综述［J］.载人航天，2016，22（1）：45⁃53.Zeng Lei，Sun Pengfei，Chen Ming.Review of underwater test and key technologies of space manipulator［J］.Manned Spaceflight， 2016，22（1）：45⁃53.（in Chinese）

［4］ 高峰，易旺民，郭涛.一种用于空间机械臂的微重力模拟悬吊配重试验系统［J］.航天器环境工程，2014，31（1）：52⁃56.Gao Feng，Yi Wangmin，Guo Tao.A micro⁃gravity suspension test facility for space manipulators［J］.Spacecraft Environment Engineering，2014，31（1）：52⁃56.（in Chinese）

［5］ 张崇峰，陈宝东，郑云青.航天器对接机构［M］.上海：科学出版社，2016：191⁃198.Zhang Chongfeng，Chen Baodong，Zheng Yunqing.Spacecraft Docking Mechanism［M］.Shanghai： Science Press，2016：191⁃198.（in Chinese）

［6］ 梅凤翔.工程力学［M］.北京：北京理工大学出版社，1999：642⁃648.Mei Fengxiang.Engineering Mechanics［M］.Beijing： Beijing Institute of Technology Press，1999：642⁃648.（in Chinese）

［7］ Syromiatnikov V S.Manipulator system for module re docking on the Mir Orbital Complex［C］ ／／Robotics and Automation，1992.Proceedings.，1992 IEEE International Conference on.IEEE， 1992： 913⁃918.

［8］ 徐志刚，白鑫林，王军义.基于等效惯量模拟的空间站转位机械臂承载性能测试［J］.机器人，2015，37（2）：231⁃236.Xu Zhigang，Bai Xinlin，Wang Junyi.Load carrying capacity test of the space station redocking manipulator Based on the E⁃quivalent Inertia Simulation Method［J］.Robot， 2015，37（2）：231⁃236.（in Chinese）

［9］ 申永胜.机械原理教程［M］.北京：清华大学出版社，1999：21⁃22.Shen Yongsheng.Spacecraft Docking Mechanism［ M］.Bei⁃jing： Tsinghua University Press， 1999：21⁃22.（in Chinese）

［10］ 李广兴，肖余之，卜劭华，等.空间站组装过程姿态控制方案研究［J］.载人航天，2012，18（1）：22⁃28.Li Guangxing， Xiao Yuzhi， Bu Shaohua，et al.Research on attitude control scheme during space station assembly［J］.Manned Spaceflight，2012，18（1）：22⁃28.（in Chinese）