L1点月球天梯绕地运行过程动力学

王晓慧，毛李恒

（北京航空航天大学宇航学院，北京100191）

1 引言

天梯概念最早由 Artsutanov于1960年提出［1］，然而他的设想并没有引起足够的关注；1975年，美国人Pearson［2］也独立提出了相关的概念，并将其发表在了期刊上，人们开始关注这一新型的运输系统；1979年，Pearson提出了月球天梯的概念，根据Pearson的描述，月球天梯是穿过地月L1点（或L2点）的一种缆绳结构，一端连着月球表面，另一端连着配重以保持平衡，攀爬器沿着缆绳上下移动来运送货物［3］。由于材料的限制，在当时看来建造一座月球天梯是不可能的。1991年，日本科学家饭岛澄男研制出了世界上第一根碳纳米管，这种材料的强度是钢的100倍，密度却只有钢的 1／6［4⁃5］。 碳纳米管的出现让月球天梯的建造变成可能。

目前对于天梯的动力学研究大都针对地球天梯。Noboru Takeichi忽略了缆绳的柔性和弹性，利用连续体模型对地球天梯缆绳释放过程的动力学问题开展了研究，并给出了天梯空间站的控制策略［6］；Paul Williams和 Pamela Woo 都对攀爬器的运行给地球天梯带来的影响进行了研究，Paul还根据天梯的动力学响应，对攀爬器的运行进行了优化［7⁃8］；Vladimir 等人利用多点模型，考虑地球引力和大气阻力，对地球天梯缆绳断裂后的坠毁过程开展了动力学研究［9］。但目前对于月球天梯的动力学研究还比较少见。

月球天梯动力学问题与绳系卫星动力学问题在本质上类似，国内外学者对绳系卫星的动力学问题开展过研究。Krupa等人利用变分原理建立了绳系卫星连续体模型的偏微分方程，进行了动力学和控制方面的研究［10］；于绍华以一组偏微分方程建立的数学模型和距离速率控制算法来描述有质绳系的受控运动，并利用递推算法求得了不可拉长绳系的驻形（即绳系的最终稳定形状）［11］；余本嵩利用一种改进的有限差分法对粘弹性有质绳系的释放过程进行了数值模拟［12］。

目前专门针对月球天梯绕地运行过程中偏离平衡位置的动力学研究还没有看到。虽然已有不少针对地球天梯和绳系卫星的动力学研究，但这些研究很少同时考虑缆绳质量、柔性和弹性，而且这些研究都只考虑地球引力对绳系的影响，月球天梯则需同时考虑地球引力和月球引力的影响，这就导致了这些研究方法无法直接用于月球天梯运行过程的动力学研究。本文采用离散体模型，同时考虑缆绳的质量、柔性和弹性，建立起月球天梯绕地运行过程动力学模型，并利用Newmark法对动力学模型进行求解，以得到月球天梯的动力学响应。

2 月球天梯绕地运行过程动力学模型

月球天梯主要由5部分组成，分别是缆绳、配重、攀爬器、空间站和月面平台［13］，其基本结构如图1所示。

2.1 定义坐标系

图1 月球天梯基本结构Fig．1 Basic architecture of lunar space elevator

假设月球公转轨道为圆轨道。为了方便动力学方程的描述和结果的展示，本文自行定义了两个坐标系：地心⁃白道惯性坐标系OE⁃xyz和月表旋转坐标系 OL⁃xyz（图 2）。 地心⁃白道惯性坐标系OE⁃xyz的原点位于地心，x⁃OE⁃y 平面与白道面重合，x轴指向初始时刻的月心位置，y轴指向该时刻的月球公转速度方向，z轴由右手定则确定。动力学方程中描述的矢量均为该惯性坐标系下的矢量。 月表旋转坐标系 OL⁃xyz的 x⁃OL⁃y 平面同样与白道面重合，原点位于地月连线与月表的交点处，x轴位于地心和月心的连线上且始终指向月心，y轴垂直于x轴指向月球公转速度方向，z轴由右手定则确定。月表旋转坐标系OL⁃xyz主要用于观察月球天梯配重的振荡轨迹。则位置矢量r在两个坐标系下的转换关系如式（1）所示。

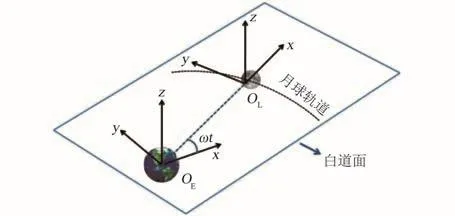
图2 坐标系定义Fig．2 Coordinate system definition

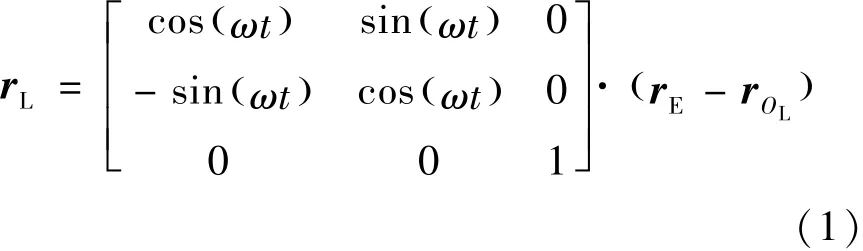
式中，rL表示t时刻物体在OL⁃xyz坐标系下的位置矢量，rE表示同一时刻该物体在OE⁃xyz坐标系的位置矢量，rOL表示该时刻OL点在OE⁃xyz坐标系的位置矢量，ω表示月球公转角速度。

2.2 缆绳离散化

本文采用离散模型来模拟月球天梯缆绳。离散方法是将缆绳看成一系列由无质量弹簧连接的质点，弹簧可伸长但不可弯曲［14］。缆绳的一端连着月表，另一端连着配重（图3）。该离散模型既能表现缆绳的柔性，也能体现弹性，同时也将缆绳的质量考虑其中。离散的质点越多，则离散缆绳模型越接近真实模型。缆绳振荡过程中，离散点个数保持不变。

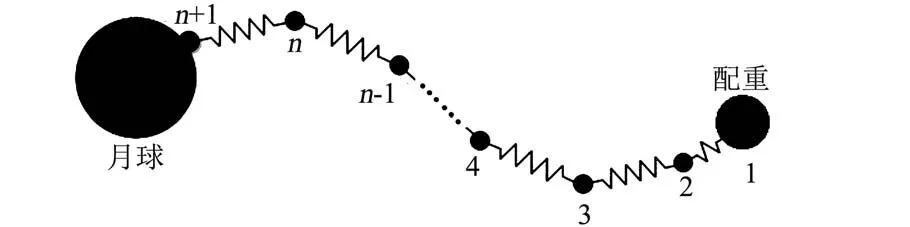
图3 月球天梯缆绳离散模型Fig．3 Discrete model of lunar space elevator

2.3 动力学方程

假设配重的质量为mc，缆绳的截面积为A，弹性模量为E，密度为ρ，每个离散单元的长度为l，质量为 m0，易知有式（2）：

根据牛顿第二定律，质点 i（i＝2，3，…，n）的动力学方程为式（3）：

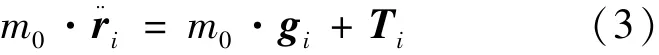
式中，gi表示质点i所处位置的引力加速度，包括地球引力和月球引力；Ti表示质点i⁃1和质点i＋1对质点i的合拉力，可分别表示为式（4）、（5）：

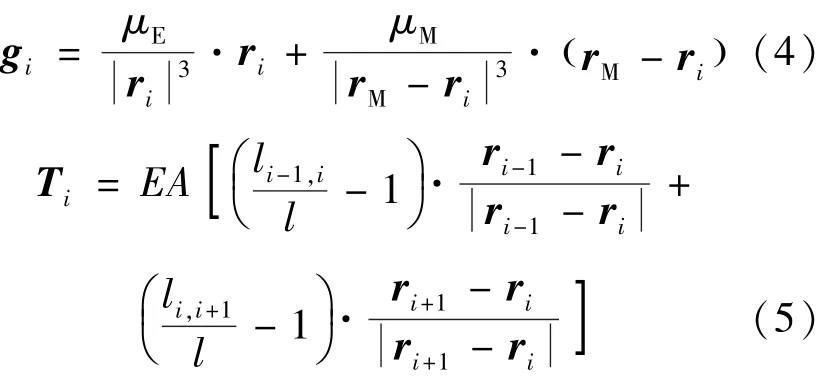
式（4）中，μE为地球引力常数，μM为月球引力常数；rM为月心位置向量。 公式（5）中，li－1，i为质点 i－1 到质点 i的实际距离，li，i＋1为质点 i到质点i＋1的实际距离，表达为式（6）：

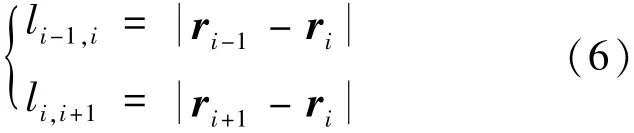
需要注意的是，公式（3）只描述了质点2到质点n的动力学方程，不包含质点1和缆绳末端重物的动力学方程。质点1（配重）的动力学方程与公式（3）相比只有拉力T1发生如式（7）所示变化：

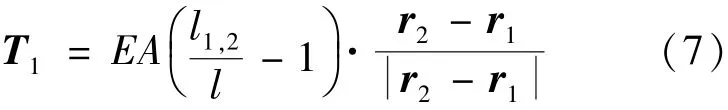
质点n＋1固连于月球表面，绕地球做匀速圆周运动，故质点n＋1的动力学方程为式（8）：

这样，我们就得到了所有n＋1个质点的动力学方程。现将公式（3）和公式（8）的等式右端统一用fi（i＝ 1，2，…，n，n ＋1） 表示，则可得到整个离散缆绳系统的动力学方程为式（9）：

其中各项满足式（10）：

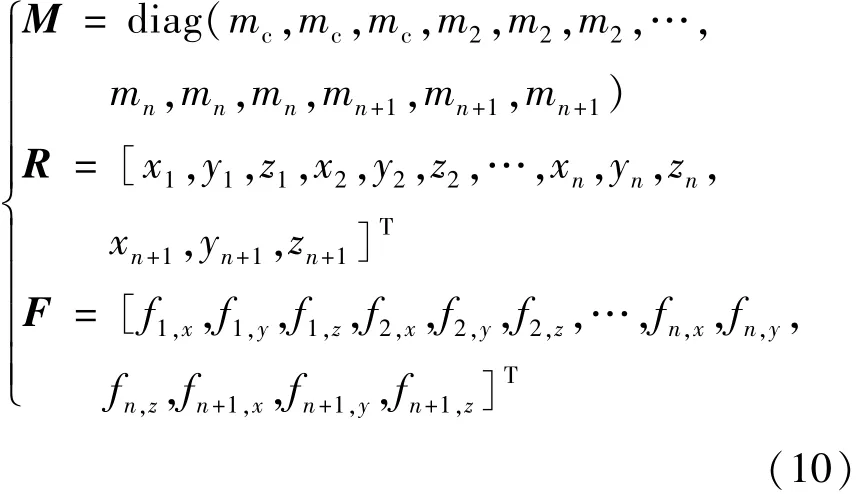
式中，m2＝m3＝… ＝mn＋1＝m0。

3 动力学方程求解方法

得到动力学方程（10）后，需选择合适的方法对其进行求解。月球天梯缆绳的总长通常超过104km，而且其振荡周期很可能达到十几天甚至几十天，这就意味着该动力学问题是一个大自由度、长历程的问题。因此，求解算法和积分步长的选择对于该问题的求解非常关键。如果积分步长太短，求解时间会变得很长，每调整一次参数都需付出很大的时间成本；如果积分步长太长，则会带来较大的误差，甚至导致算法不收敛。

经过比较，本研究选用Newmark法对方程进行求解。Newmark法是线性加速法的推广，它所采用的假定如式（11） ～（12）［15］：

公式（11）和公式（12）中，δ和α的关系为如式（13）：

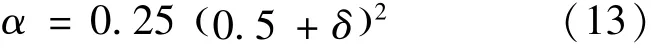
δ的几何意义如图4所示。

Newmark法的优点在于其稳定性与系统的故有频率无关，当其中的两个参数δ＝0.5、α＝0.25时，算法是无条件稳定的［15］，这将节约大量调整参数的时间；另外，Newmark法至少具有2阶精度，而该动力学问题的响应频率又比较小，因此取较大的积分步长也能得到较高的计算精度［16］，容易在计算精度和求解时长之间找到平衡。

动力学方程（10）中只含质量矩阵M，不含刚度矩阵K和阻尼矩阵C，则Newmark法的求解步骤如下：

1）形成质量矩阵 M0， 计算初始值 R0、R˙0、R¨0；

2）选取 δ、α、时间步长 Δt，计算积分常数：

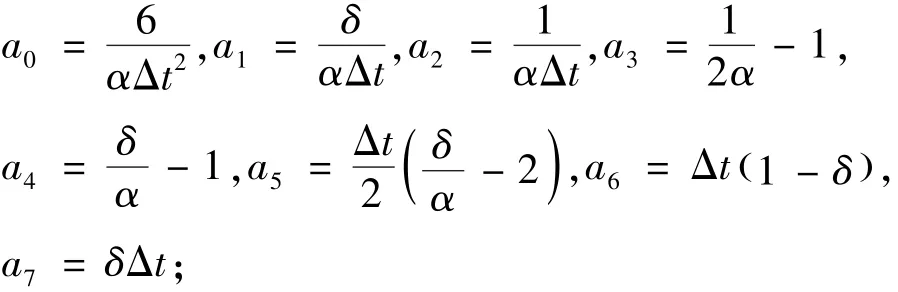
4）计算t＋Δt时刻的有效载荷：

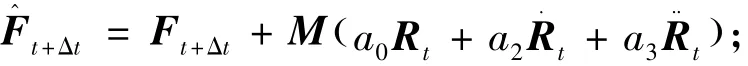
5）计算t＋Δt时刻的位移：

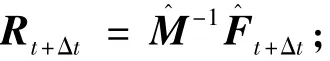
6）计算t＋Δt时刻的位移、速度和加速度：

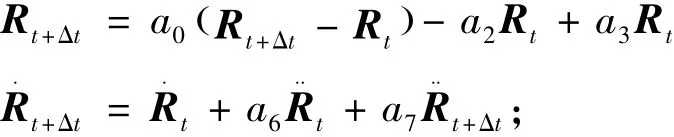
动力学方程求解流程如图5所示。

4 动力学求解及结果分析

图5 动力学方程求解流程Fig．5 The process of dynamic equation solving

各参数的取值为：地月距离R＝384400 km，月球半径 RM＝1738 km，地球引力常数 μE＝3.986×1014m3／s2，月球引力常数μM＝4.902 77 ×1012m3／s2，月球公转角速度 ω ＝2.6617×10－6rad／s，缆绳截面积A＝20 mm2，（碳纳米管材质）缆绳弹性模量E ＝1000 GPa［5］，缆绳初始应力 σ ＝ 40 GPa，缆绳密度 ρ＝1300 kg／m3，缆绳总长度 L＝200 000 km，缆绳单个离散单元长度l＝100 km，缆绳初始时刻偏离地月连线的角度θ分别取3°和5°，积分步长Δt＝0.7 s，该积分步长是综合考虑计算精度和计算时间得到的，一方面，通过初步计算发现，Δt取0.1 s和0.7 s结果没有明显差别；另一方面，当Δt取0.7 s时，仿真10 d所需的计算时间约为1 h（CPU： Intel Core i7⁃4790； 软件： Matlab 2016a），该计算效率可接受。

配重质量可根据以上数据计算得到。配重受力如图6所示。

图6 配重受力分析Fig．6 The force condition of counterweight

图中，FE为地球引力，FL为月球引力，T为缆绳拉力，F为离心力。受力平衡方程为式（14）：

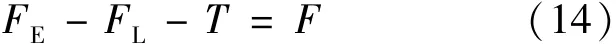
将各力的具体表达式及数据代入公式（14）求得配重质量mc＝8.12×104t。

为了进行对比分析，同时对不考虑缆绳弹性时的动力学问题进行了研究。本文的处理方法为：将缆绳的弹性模量设置为碳纳米管的1000倍（即1000 TPa），此时，若缆绳应力为40 GPa，则缆绳的变形不会超过0.004%，可近似认为没有弹性。

因为缆绳所受的力均在白道平面内，故只考虑缆绳在白道平面内的运动，如图7。

图7 θ角定义Fig．7 Definition of θ

当缆绳初始偏离角分别为3°和5°时，配重的振幅如图8所示。从图中可以看出，配重偏离平衡位置后将做周期性振荡，月球天梯并不会坠毁。产生周期性振荡的原因是当配重偏离地月连线时，地球引力和月球引力会产生一个垂直于地月连线的分力，配重在该分力的作用下持续振荡。配重的振幅基本保持不变，若考虑缆绳弹性，则偏离3°时的振幅约为1.125×104km，偏离5°时的振幅约为1.864×104km，二者的振荡周期基本一致，约为6.7 d。若忽略缆绳弹性，则偏离3°时的振幅约为1.047×104km，偏离5°时的振幅约为1.743×104km，振荡周期约为7.0 d。忽略缆绳弹性时振幅稍小，原因是此时缆绳没有弹性变形。

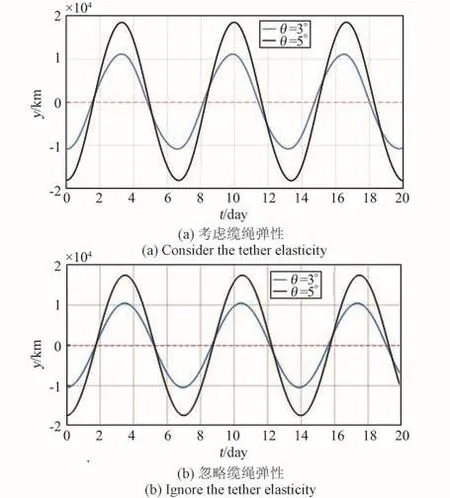
图8 缆绳振幅Fig．8 The amplitude of counterweight

配重的振荡速度如图9所示，若考虑缆绳弹性变形，配重偏离3°时的最大振荡速度约为135 m／s，偏离5°时的最大振荡速度约为208 m／s。若不考虑缆绳弹性变形，配重偏离3°时的最大振荡速度约为110 m／s，偏离5°时的最大振荡速度约为182 m／s。不考虑缆绳弹性变形时最大振荡速度稍小，原因是此时缆绳的振幅小，回复力做功少。

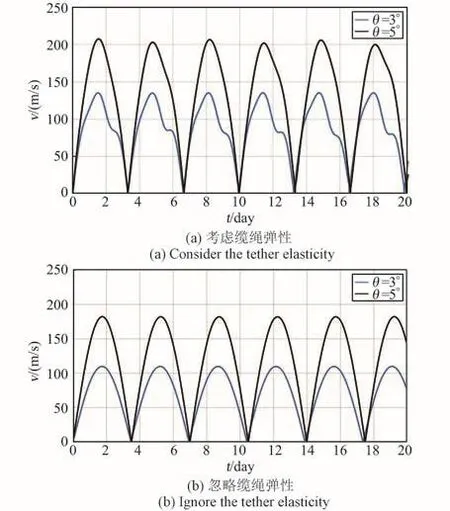
图9 缆绳振荡速度Fig．9 The hunting speed of counterweight

配重在三个振荡周期里的运动轨迹（月表旋转坐标系OL⁃xyz下）如图10所示。我们发现，若考虑缆绳弹性（如图10（a）和（b）），配重并不是做简单的单摆运动，而是在做y方向振荡的同时，还伴随着x方向的振荡。初始偏离角越大，x方向的振荡范围也越大，初始偏离角为3°时x方向的最大振荡范围约为4381 km，初始偏离角为5°时约为5275 km。如果忽略弹性（如图10（c）），则配重的振荡轨迹接近一段圆弧，与预期相符。

配重在振荡过程中缆绳应力的变化情况如图11所示。考虑弹性时，缆绳的最大应力约为60 GPa，相对于40 GPa的初始应力来讲，增大了约50%。这一结果提醒我们，月球天梯缆绳的工作应力不应该过大，否则在振荡过程中很可能导致缆绳断裂。不考虑弹性时，最大应力均没有超过45 GPa，主要原因是此时没有x轴方向的振荡。

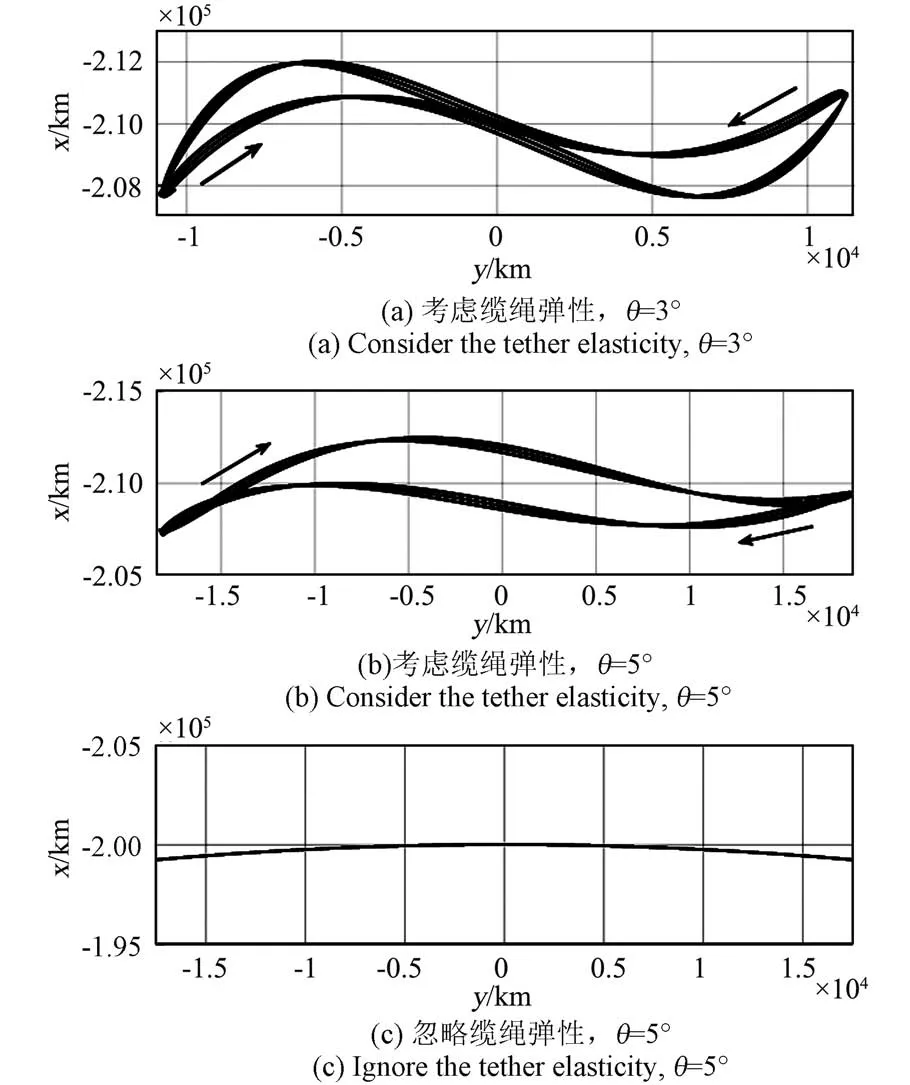
图10 配重运动轨迹Fig．10 Path of counterweight

图11 缆绳应力Fig．11 Tether Stress

以上结果都是不加任何控制的自由振荡结果，我们同时对施加一定反向推力的振荡过程开展了研究。现假设配重的初始偏离角为5°，考虑缆绳弹性，在配重上施加一个10 000 N的持续推力抑制振荡，该推力由配重上的反推发动机提供，方向始终垂直于地月连线。最终得到配重的振幅变化过程如图12所示。从图中可以看出，大约经过3天配重就可回到平衡点附近，由于推力的存在，配重并没有完全回到平衡点。振荡速度的变化如图13所示，振荡过程中的最大速度约为102 m／s。

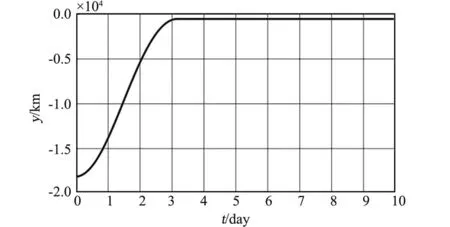
图12 缆绳振幅（受控条件下）Fig．12 The amplitude of counterweight（under con⁃trol）

缆绳的应力变化过程以及配重的运动轨迹分别如图14和图15所示。缆绳的最大应力约为46 GPa。

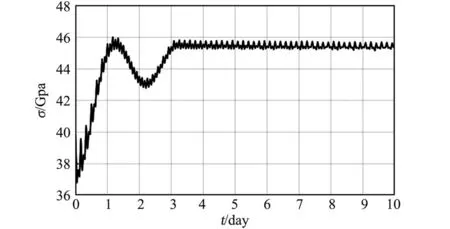
图14 缆绳应力（受控条件下）Fig．14 Tether Stress （under control）

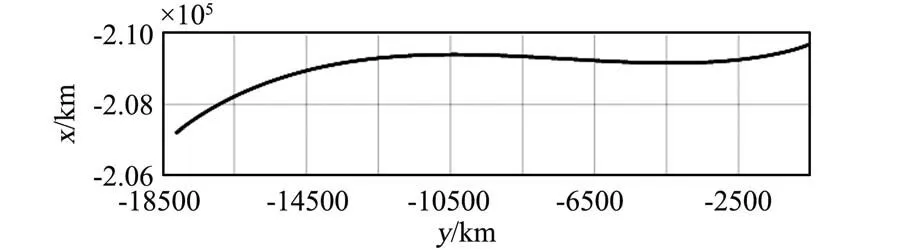
图15 配重运动轨迹（受控条件下）Fig．15 Path of counterweight （under control）

5 结论

1）月球天梯偏离平衡位置后不会坠毁，而是会在一定范围内振荡，如果不加控制，振幅基本保持不变，且振荡周期与初始偏离角基本无关。

2）月球天梯在振荡过程中，缆绳应力最多会增大50%左右，因此，缆绳的工作应力不应太大，否则可能导致缆绳断裂。

3）通过对比发现，若不考虑缆绳弹性，则月球天梯的振幅较小，振荡形式较简单，振荡过程中的最大应力较小，很可能会低估振荡的危险性，因此，开展天梯动力学仿真时，考虑缆绳弹性是必要的。

4）如果在配重上施加一定的控制力，月球天梯能够在较短时间内回到平衡位置附近。受控条件下缆绳应力及振荡速度都较小。

本文求得的动力学响应能为未来月球天梯的运行和控制提供一定的参考。

（

）

［1］ Artsutanov Yuri.V Kosmos na Electrovoze［N］.Komsomol⁃skaya Pravda， 1960⁃07⁃31.Artsutanov Yuri.Into Space on a Train［N］.Komsomolskaya Pravda， 1960⁃07⁃31. （in Russian）

［2］ Pearson J.The orbital tower：a spacecraft launcher using the Earth’s rotational energy［J］.Acta Astronautica， 1975， 2（9⁃10）： 785⁃799.

［3］ Pearson J.Anchored lunar satellites for cislunar transportation and communication ［ J］.Journal of the Astronautical Sci⁃ences， 1979， 27（1）： 39⁃62.

［4］ Iijima S.Helical microtubules of graphitic carbon［J］.Na⁃ture， 1991， 354（6348）： 56⁃58.

［5］ Ruoff R S，Qian D，Liu W K，et al.Mechanical properties of carbon nanotubes：theoretical predictions and experimental measurements［J］.Comptes Rendus Physique， 2003， 4（9）：993⁃1008.

［6］ Takeichi N.Geostationary station keeping control of a space elevator during initial cable deployment［J］.Acta Astronauti⁃ca， 2012， 70（1⁃2）： 85⁃94.

［7］ Williams P，Ockels W.Climber motion optimization for the tethered space elevator［J］.Acta Astronautica， 2010， 66（9）： 1458⁃1467.

［8］ Woo P，Misra A K.Dynamics of a partial space elevator with multiple climbers［J］.Acta Astronautica， 2010， 67（7）：753⁃763.

［9］ Aslanov V S，Ledkov A S，Misra A K， et al.Dynamics of space elevator after tether rupture［J］.Journal of Guidance，Control， and Dynamics， 2013， 36（4）： 986⁃993.

［10］ Krupa M，Poth W，Schagerl M，et al.Modeling，dynamics and control of tethered satellite systems［J］.Nonlinear Dy⁃namics， 2006， 43（1⁃2）： 73⁃96.

［11］ 于绍华，刘强.有分布质量绳系的卫星系统的动力学［J］. 宇航学报，2001， 22（3）：52⁃61.Yu Shaohua， Liu Qiang.Dynamics of mass⁃distributed tether system［J］.Journal of Astronautics， 2001， 22（3）： 52⁃61.（in Chinese）

［12］ 余本嵩，文浩，金栋平.时变自由度绳系卫星系统动力学［J］. 力学学报，2010， 42（5）：926⁃932.Yu Bensong， Wen Hao， Jin Dongpin.Dynamics of tethered satellite system with a time⁃varying number of degrees⁃of⁃free⁃dom［J］.Chinese Journal of Theoretical and Applied Mechan⁃ics， 2010， 42（5）： 926⁃932.（in Chinese）

［13］ Pearson J， Levin E， Oldson J， et al.The Lunar space eleva⁃tor［C］ ／／55th International Astronautical Congress， Vancou⁃ver， Canada， 2004.

［14］ 余本嵩.复杂太空环境下柔性绳系卫星动力学与控制［D］.南京：南京航空航天大学，2011.Yu Bensong.Dynamics and Control of Flexible Tethered Sat⁃ellite in Complex Space Environment［D］.Nanjing： Nanjing University of Aeronautics and Astronautics， 2011.（ in Chi⁃nese）

［15］ 李东旭.高等结构动力学［M］.长沙：国防科技大学出版社， 1997： 161⁃163.Li Dongxu.Advanced Dynamics of Structures［M］.Chang⁃sha： National University of Defense Technology Press， 1997：161⁃163.（in Chinese）

［16］ Bathe K J， Wilson E L.Stability and accuracy analysis of di⁃rect integration methods［J］.Earthquake Engineering and Structural Dynamics， 1997， 1（3）： 283⁃291.