月地低能返回轨道最优控制策略研究

刘 玥，付凯林，荆武兴，钱霙婧

（1.航天东方红卫星有限公司，北京100094；2.哈尔滨工业大学航天学院，哈尔滨150001；3.北京工业大学机械工程与应用电子技术学院，北京100022）

1 引言

从月球返回是我国探月工程“绕、落、回”三步走中的第三步，从月球返回地球的转移轨道对飞船燃料需求很大，特别是未来对月球的开发中，需要将大量月球资源送回地球使用，传统的双曲拼接转移轨道需要飞船在环月轨道施加超过880 m／s的速度增量，大载荷货运任务往返代价很高［1⁃2］。 月地低能返回轨道是一种适用于无人、大载荷货运任务的月地返回轨道，研究表明：飞船可从环月驻泊轨道出发，以最低约603 m／s的切向速度增量，经地月L2平动点附近逃离月球影响球范围，进而转移至地日平动点Halo轨道附近的区域，最终返回地球，整个返回过程耗时约100天，可节约约 25%的速度脉冲［3⁃4］。 由于其节能特性，月地低能返回轨道允许飞船携带更多物资载荷返回地球，在未来的月球开发任务中将扮演重要角色。

然而，月地低能返回轨道对飞船轨道控制精度要求苛刻。以传统的月球返回轨道为例，初始的位置和速度误差在终端可被放大数千倍，且在月地低能返回轨道中，这种效应更为明显［5］。因此，若保证飞船再入点轨道精度，则入轨点的控制精度需求将过于严苛以至于工程上难以实现。对此情况，若飞船入轨点出现偏差，则必须引入轨道控制以消除入轨偏差带来的影响。传统的地月系统转移任务由于轨道尺度较小，动力学环境也较为简单，因此飞船轨道控制的时机通常选择在转移初期执行，以避免轨道误差随转移时间积累［6］。但是月地低能返回轨道由于飞船需要途经地日和地月系统平动点附近的引力混沌区，动力学环境极其复杂，因此修正脉冲的误差也可能对再入点参数造成较大影响。在此情况下，需要重新规划精确控制再入点参数的轨道控制策略，既保证终端参数的精度，又兼顾节省燃料消耗的目的。对于此类弱稳定轨道的控制问题，有学者作了相关的研究。例如，Parker和Marchand分别对传统地月转移轨道的敏感性和轨控燃料消耗特性进行了研究［7⁃8］，而 Renk 和 Folta 则针对弱稳定轨道设计了轨道保持控制策略［9⁃10］，以上研究均是月地低能返回轨道控制策略设计的重要参考。

此外，在月地低能返回任务中，飞船定轨精度与地月距离密切相关且定轨的误差也直接影响着轨道修正的精度。例如，月球逃逸阶段，激光测距定轨技术可为飞船提供米级精度的轨道确定数据［11］；而飞船地日转移阶段，由于地月距离过大，只能依靠甚长基线干涉测量定轨（VLBI），在地日平动点附近，其精度只能在22 km左右［12］。因此，轨道确定的误差将对轨道控制脉冲的计算产生较大影响，轨道控制策略需要进一步深入研究和设计。

本文为解决低能返回轨道入轨控制精度要求苛刻、工程实现性较差的问题，通过分析计算轨道初始飞行状态误差的传播特性与轨道对控制脉冲的敏感度，设计节约燃料的轨道偏差修正策略，并对所设计的修正策略进行带有控制和测量误差的仿真打靶，以验证控制策略的有效性。

2 动力学与轨道分析

2.1 动力学模型

由于地球、太阳、月球的引力对于飞船返回过程均有明显影响，特别是货运飞船逃逸月球阶段，飞船轨道受日月引力与月球椭圆运动影响极为剧烈。因此，有必要引入椭圆四体动力学模型，以准确反映飞船在日地月系统中的运动。

椭圆四体动力学模型在地月旋转坐标系中建立，Oc为坐标系原点，位于地月质心，X和Z轴分别指向月球质心和地月角动量方向，Y轴与另外两轴形成右手系，如图1所示。在地月旋转坐标系下，飞船的动力学方程如式（1）［3］：

图1 椭圆四体模型Fig．1 Elliptical four⁃body model

其中，ω为地月旋转系的角速度矢量，rpe、rpm、rps为地球、月球和太阳到飞船的位置矢量，μe、μm、μs为地球、月球和太阳的引力常数， rs为太阳相对地月质心的位置矢量。

2.2 月地低能返回轨道设计

椭圆四体模型下，月地低能返回轨道可以通过选择合适的飞船初始飞行状态来获得。本文假设飞船初始轨道为一个100 km高的环月白道圆轨道［13］，对从环月轨道上任意时刻从不同月心经度位置上出发，施加不同切向速度脉冲后飞行器的运行轨迹进行遍历搜索，寻找能够返回地球的最省能量轨道方案。经过搜索得到，在2020年1月5日，当运行至月心经度为224°时，对飞船施加623 m／s的切向脉冲，而后飞船经地月L2平动点附近逃逸月球影响球进入低能返回轨道，整个返回任务大约耗时129天，飞船与地球的最远距离约为1 325 200 km，再入点高度为130 km。返回轨道在地月旋转系（Earth⁃Moon Rotating Frame， EMRF）和地日旋转系（Earth⁃Sun Rotating Frame，ESRF）下的仿真图如图2和图3所示。

图2 地月旋转系下的低能返回轨道Fig．2 Low energy moon return trajectory in EMRF

图3 地日旋转系下的低能返回轨道Fig．3 Low energy moon return trajectory in ESRF

利用此方式返回地球，可以节约大约23%的总速度脉冲［4］，但飞船入轨精度对再入点的影响需要进一步分析。

3 月地低能返回轨道控制策略设计

3.1 初始状态误差传播特性

由于导航和轨道控制偏差，飞船并不能精确进入标称返回轨道，因此再入点参数会出现偏差，甚至不能满足终端再入需求。

为定量描述入轨偏差对再入点高度的影响，本文引入了协方差分析法对其进行分析。

定义 δX ＝ [δT0δx0δv0]为飞船入轨时刻、入轨位置和入轨速度偏差，δH为再入点高度的偏差，二者有式（2）所示关系：

其中， Γ ( tf，t0)为初始状态到再入点轨道高度的状态转移矩阵，因此，终端再入点轨道高度的协方差矩阵可以写为式（3）所示形式：

其中， E[ δX· ( δ X)T]为初始飞行状态的协方差，由上式即可计算初始轨道误差到终端再入点参数的误差传播特性。本文中，初始飞行状态的偏差可以写为式（4）所示具有高斯分布特性的对角阵形式［14］。

由上式可以计算得到初始飞行状态与终端再入点高度误差协方差关系如图4所示。

图4 初始状态误差传播特性Fig．4 The propagation properties of initial state er⁃rors

图中可以看出，再入点高度的误差协方差与初始状态误差协方差基本呈线性关系，且再入点高度对初始飞行状态及其敏感，若保证再入点高度误差在2 km以内，则入轨时刻、位置和速度的误差不能超过2 s、60 m和8 cm／s。这样的入轨精度，以现有嫦娥2号高精度变轨技术水平，相对精度为0.1%，对600 m／s以上的变轨速度增量而言，仍可能造成超过0.6 m／s的速度增量误差，仍不能满足终端再入条件［15］。因此必须引入轨道控制以消除再入点高度偏差。

3.2 轨道控制策略设计

考虑到月地低能返回轨道动力学环境的复杂性和导航控制系统所能提供的入轨精度无法满足低能返回轨道终端再入点条件，有必要设计一种尽可能节省修正燃料消耗的轨道修正策略。本文采取与协方差分析法类似的手段，研究轨道上不同位置的随机控制量到终端再入点高度的误差传播特性，以建立轨道对修正的敏感度模型。因此，可将再入点高度与修正脉冲的关系式表示为式（5）：

其中，Γm为修正点飞行状态到终端再入点高度的状态转移矩阵，δv＝σv为具有高斯分布特性的修正速度脉冲，λ为加权系数，用于反映导航误差对轨道修正的影响。由式（5）可以得到图5所示返回轨道对在其不同位置施加修正的敏感程度，用再入点高度与修正脉冲大小的协方差之比表示。

图5 再入高度敏感性Fig．5 Sensitivity of reentry altitude

图5 存在两个峰值，分别位于飞船到达地月L2平动点附近和到达远地点的时刻。在这两个位置上，返回轨道再入点高度对修正脉冲最为敏感，可以利用最小的修正量实现再入点高度偏差的消除，从而节约了修正所需的燃料。这种敏感性带来的缺陷是轨道同样对修正误差较为敏感，若修正量存在偏差，则此偏差仍然会对再入点高度造成较大影响，为解决此问题，需要加入额外的一次补充修正以消除前两次修正遗留的轨道偏差。综上，可以设计优化的轨道修正策略如下：

修正点A：当飞船到达地月L2点时进行修正

修正点B：当飞船到达远地点时进行修正

修正点C：当飞船再次到达地月系统之内（星地距离再次小于380 000 km时）进行补充修正。

在各修正点，根据测量到的飞船飞行状态，按照式（6）～（7）所示牛顿迭代法计算修正脉冲。

4 仿真验证分析

为验证本文提出的轨道修正策略的有效性，采用蒙特卡洛打靶法对返回轨道进行仿真，分析对具有随机初始偏差的低能返回轨道进行三脉冲修正后再入点高度的控制结果，使用2.2节中算例的轨道作为打靶仿真的标准轨道，表1为仿真使用的低能返回轨道初始参数。

表1 低能返回轨道初始参数Table 1 Initial parameters of the low energy Moon re⁃turn trajectory

利用此初值生成标称轨道，将表2中给出的入轨和控制误差源，代入标称轨道中进行修正策略仿真计算，验证修正策略的有效性。

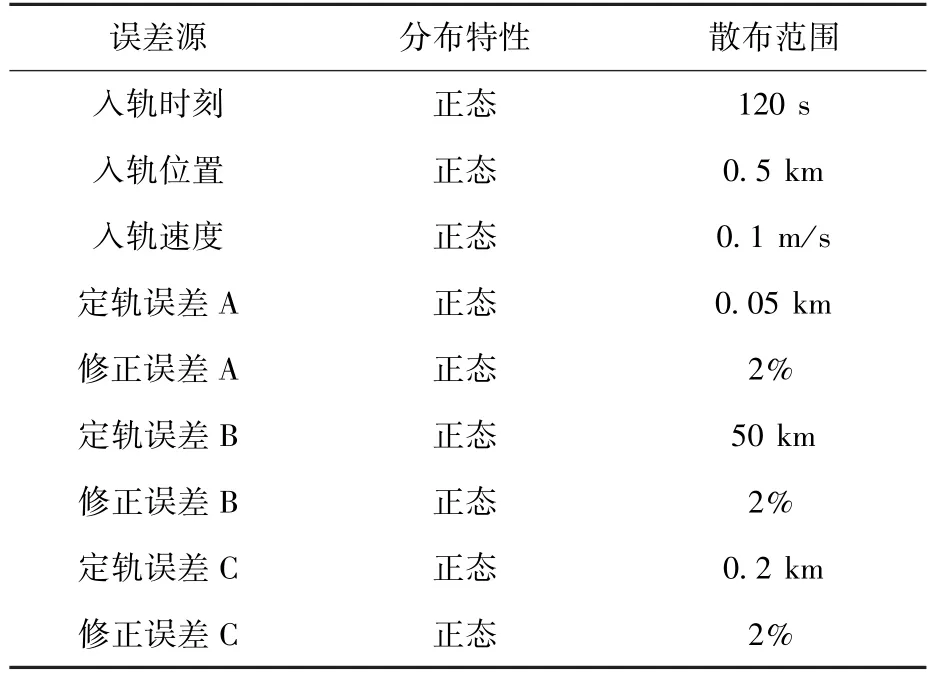
表2 月球低能返回轨道误差源Table 2 Error resource for low energy moon return trajectory

按照以上入轨误差数据，所形成的轨道不可能满足再入点高度约束条件，必须实施轨道修正。本文使用蒙特卡洛打靶法进行1000次打靶计算，修正策略使用前一节提出的三点修正策略，计算结果的散布情况如图6～9所示。

图6 再入高度采样Fig．6 Sampling of reentry altitude

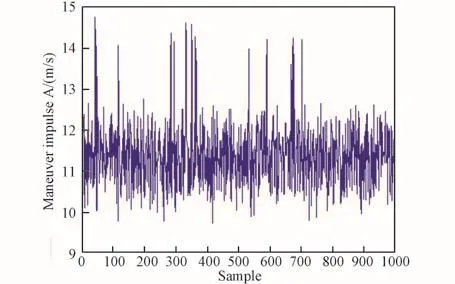
图7 第一次脉冲大小采样Fig．7 Sampling of the first pulse

图6 中低能返回轨道再入点高度基本控制在130±2 km以内，说明本文提出的三脉冲修正策略可以有效消除再入点高度偏差，可满足低能返回轨道终端约束条件。

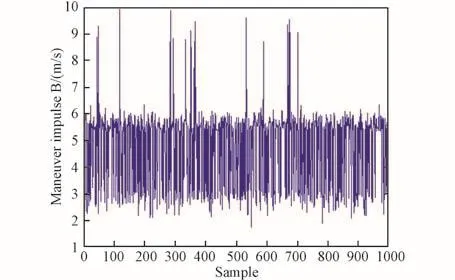
图8 第二次脉冲大小采样Fig．8 Sampling of the second pulse

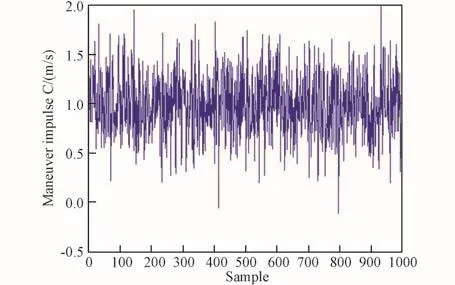
图9 第三次脉冲大小采样Fig．9 Sampling of the third pulse

从图7～9中可以看出，三次修正脉冲的大小平均值保持在12 m／s、5 m／s和1.5 m／s以内，而总修正脉冲保持在20 m／s以内，仅占整个任务所需变轨脉冲大小的约3.2%。可以得出结论：本文提出的三脉冲修正策略可有效精确控制月地低能返回轨道终端参数。

图10和图11所示为修正轨道仿真结果，分别在地月旋转坐标系下和地日旋转坐标系下绘制，可以明显看出三次修正脉冲的施加位置，分别位于月球L2平动点附近、飞行器远地点以及月球轨道边界处。

5 结论

本文提出的三脉冲轨道修正策略按照低能返回轨道对修正脉冲的敏感性设计修正时机，并在考虑定轨误差的前提下计算修正脉冲，可以有效地消除再入点高度偏差。

图10 地月旋转系下的轨道修正仿真结果Fig．10 Simulation result of orbit correction in EM⁃RF

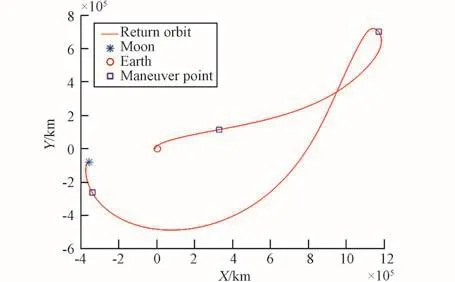
图11 地日旋转系下的轨道修正仿真结果Fig．11 Simulation result of orbit correction in ESRF

（

）

［1］ Perino M A，Fenoglio F，Pelle S，et al.Outlook of possible European contributions to future exploration scenarios and ar⁃chitectures［J］.Acta Astronautica， 2013（1）： 25⁃34.

［2］ Stansbery E K，Draper D S.The role of sample return and sample science in low cost missions［J］.Acta Astronautica，2014（1）： 453⁃459.

［ 3 ］ Ivashkin V V.On particle’s trajectories of Moon⁃to⁃Earth space flights with the gravitational escape from the lunar at⁃traction［J］.Doklady Physics.MAIK Nauka／Interperiodica，2004（9）： 539⁃542.

［4］ 荆武兴，刘玥.椭圆三体问题下月球L2低能逃逸轨道设计［J］.航空学报， 2014， 35（6）： 1496⁃1504.Jing W，Liu Y.Designing of the optimal energy escaping orbit of Lunar probe from L2 point in elliptical three⁃body problem［J］.Acta Aeronautica et Astronautica Sinica，2014，35（6），1496⁃1504.（in Chinese）

［5］ Liu Y，Qian Y J，Ma L，et al.A comparison of accuracy and efficiency of three control strategy design methods for low en⁃ergy moon return mission［C］ ／／Chinese Control and Decision Conference （CCDC），May 25⁃27，2014，Changsha， China.

［6］ 周文艳，杨维廉.月球探测器转移轨道的中途修正［J］.宇航学报， 2004， 25（1）：89⁃92.Zhou W Y， Yang W L.Mid⁃correction of trans⁃lunar trajecto⁃ry of lunar explorer［J］.Journal of Astronautics， 2004， 25（1）：89⁃92.（in Chinese）

［7］ Marchand B G，Scarritt S K，Pavlak T A，et al.A dynamical approach to precision entry in multi⁃body regimes： Dispersion manifolds［J］.Acta Astronautica， 2013（1）：107⁃120.

［8 ］ Parker J S， Anderson R L.Targeting low⁃energy transfers to low lunar orbit［J］.Acta Astronautica， 2013（1）：1⁃14.

［ 9 ］ Renk F， Landgraf M.Sun⁃Earth libration point transfer op⁃tions with intermediate HEO［J］.Acta Astronautica， 2012（1）： 1⁃19.

［10］ Folta D C， Pavlak T A， Haapala A F， et al.Earth⁃Moon li⁃bration point orbit station keeping： theory， modeling， and op⁃erations［J］.Acta Astronautica， 2014（1）： 421⁃433.

［11］ Vetrisano M，Branco J，Yarnoz D G， et al.Deflecting small asteroids using laser ablation： deep space navigation and as⁃teroid orbit control for light touch 2 mission［C］ ／／Guidance，Navigation， and Control and Co⁃located Conferences， August 19⁃22， 2013， Boston， MA：1⁃21.

［12］ Feng D Z，Guo H H，Wang X， et al.Autonomous orbit de⁃termination and its error analysis for deep space using X⁃ray pulsar［ J］.Aerospace Science and Technology， 2014， 32（1）： 35⁃41.

［13］ Li J， Gong S， Baoyin H.Generation of multisegment lunar free⁃return trajectories［ J］.Journal of Guidance， Control，and Dynamics， 2013， 36（3）： 765⁃775.

［14］ 郑爱武，周建平，胡松杰.月地返回轨道控制误差传播及分离点位置精度分析［J］.系统工程与电子技术，2012，34（12）： 2529⁃2534.Zheng Aiwu， Zhou Jianping， Hu Songjie.Error propagation control of Moon⁃to⁃Earth return trajectory and position accura⁃cy evaluation of separation point［ J］.Systems Engineering and Electronics， 2012， 34（12）： 2529⁃2534.（in Chinese）

［15］ 黄江川，宗红，李骥，等.嫦娥二号卫星高可靠高精度变轨控制技术［J］.中国科学：技术科学，2013（7）：727⁃732.Huang Jiangchuan， Zong Hong， Li Ji， et al.Orbit control technology for Chang’ e⁃2 satellite with high reliability and high precision［J］.SCIENTIA SINICA Technologica， 2013（7）：727⁃732.（in Chinese）