计算气井临界携液流量的新方法

郭布民，敬季昀，周 彪

（中国海洋石油集团中海油田服务股份有限公司油田生产研究院，天津 300459）

准确预测气井临界携液流量对于排除气井井底积液、优化气井生产制度十分重要。最早Turner通过建立气流中的液滴模型推导得出了气井临界携液流量公式[1]。后来国内外学者在Turner公式的基础上通过对其携液系数进行修正，得到了不同的表达式，主要包括Coleman公式[2]、李闽公式[3]等。然而这些公式存在以下两个问题：（1）将表面张力及气体偏差系数取为常数，忽略了其随温度、压力变化对计算临界携液流量产生的影响；（2）公式不具有普遍适用性，将这些公式应用于具体某一气田时均存在一定的误差[4]。为此，本文首先对公式中的表面张力及气体偏差系数进行了修正，并对将其取为常数所产生的计算误差进行了分析，然后对常规公式不具有普遍适用性的原因进行了探讨，并在此基础上给出了一种应用气田流温流压梯度测试资料推导携液系数的新方法，利用该新方法即可得到适用于不同气田的临界携液流量公式。

1 表面张力及气体偏差系数的修正

归纳常规的气井临界携液流量公式可得其通用表达式：

式中：qSC-标况下产气量，m3/d；A-油管截面积，m2；p-压力，MPa；T-温度，℃；Z-气体偏差系数；vg-井筒气体临界携液流速，m/s；ρl-液体密度，kg/m3；ρg-气体密度，kg/m3；σ-气液表面张力，N/m；R-摩尔气体常数，0.008 471；γg-天然气相对密度；k-携液系数，无因次。

在式（1）中表面张力σ和气体偏差系数Z均被取为常数而忽略了其随温度、压力的变化[1-3]（Turner公式、Coleman公式、李闽公式中的σ均取值60 mN/m，Turner公式和Coleman公式的Z取值0.88，李闽公式中的Z取值0.85），但实际上Z是温度T、压力p的函数，σ也并不是一定值。其中气体偏差系数采用Hall-Yarborough方法即可求解[5]，Sutton在 Firoozabadi&Ramey方法的基础上通过拟合实验数据对天然气-地层水表面张力计算方程进行了校正[6]：

式中：ρw-井筒温度压力下的地层水密度，kg/m3；T-井筒温度，℃。

从式（2）可以看出，天然气-地层水表面张力σ是ρg、T 的函数，而 ρg由 p、T 决定，因此 σ 也可写作 p、T的函数。从而式（1）可修正为以下形式：

接下来利用式（2）～（4）计算了不同温度、压力（0～120℃，0～36 MPa）下表面张力和气体偏差系数取作常数（σ=60 mN/m，Z=0.88）的误差及将其取作常数时为临界携液流量计算带来的影响（见图1～图3）。

从图1可以看出当σ取值为常数时，在较低压力（0～7 MPa）和较高压力（＞23 MPa）存在较大误差，最大误差达到25.1%。从图2可以看出当Z取为常数时，在中压低温区（8 MPa～24 MPa，0～33 ℃）存在较大误差，最大误差达到26.5%。

从图3可以看出，在中压低温条件及高压条件下忽略σ和Z的变化将为临界携液流量计算带来较大的误差。在压力8 MPa～17 MPa，温度0～18℃范围内σ和Z取常数带来的临界携液流量计算误差为9%～11%；在压力＞30 MPa的范围内σ和Z取常数带来的临界携液流量计算误差为10%～16%甚至更高。

2 携液系数推导方法的改进

通过对气流中的液滴模型进行受力分析即可得到如式（1）的临界携液流量公式，其中对携液系数k的推导则是该公式的关键。之前携液系数k的推导主要集中在对液滴形状的修正[3]，然而Taitel等指出[7]液滴临界韦伯数取值的不同将导致公式中的携液系数k发生变化。根据Turner等[1]的推导，携液系数k可表达为以下形式：

其中 a和 Cd可由式（6）进行计算[9]：

图1 σ取常数的误差

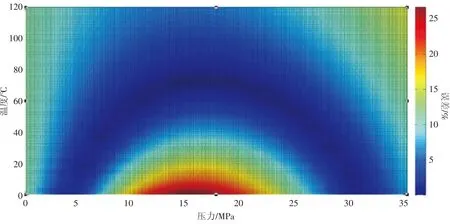
图2 Z取常数的误差

图3 σ和Z取常数为临界携液流量计算带来的误差

式中：g-重力加速度，9.8 m/s2；Wecrit-液滴临界韦伯数；a-液滴变形系数；Cd-曳力系数。

由式（6）可知，只要确定了Wecrit就可求出a及Cd，因此结合式（5）可以看出携液系数k是液滴临界韦伯数Wecrit的函数。Hanson等[8]实验测得水滴的Wecrit在1～47变化。由气田生产实践也可得出，因各气田气流携带的最大液滴尺寸和对应的临界韦伯数并不相同，所以其适用的携液系数k相差较大[9，10]，从而导致常规临界携液流量公式不具有普遍适用性。然而目前尚无可靠的临界韦伯数数理求解公式，因此无法仅凭数理计算来确定适用于某一特定气田的携液系数k。

由于式（1）同时也被认为是流体流型转变为环雾流的判定依据[7]，所以井筒内为环雾流则是气井能连续携液的必要条件。因此可以先利用气田的流温流压梯度测试数据确定相应的环雾流临界点，再利用这些环雾流临界点进行反算、拟合得到适用于该气田的携液系数k。这里以我国西部LM气田为例进行介绍，该气田四口积液井的流温流压梯度测试曲线（见图4）。

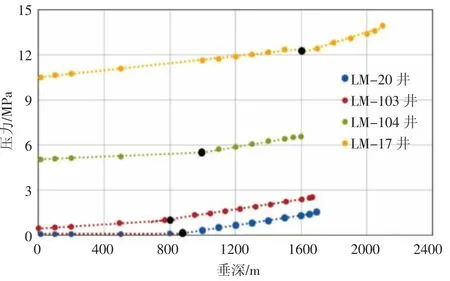
图4 LM气田四口井底积液井流温流压梯度测试曲线

图4中四口气井虽然井底积液，但井口能够连续携液，Riza等[11]通过计算深度对临界携液流量的影响对这种现象进行了分析，并指出这种情况下从井口到井底会出现从环雾流到搅动流或段塞流的变化。这里通过拾取压力梯度拐点获取环雾流的临界点（见图4），并在前文修正表面张力及气体偏差系数的基础上根据式（4）计算环雾流临界点所对应的vg和，具体（见表1）。

利用表1中的 vg和做过原点的直线（见图5）。

由图5可得，vg与成一条斜率为2.032过原点的直线，较高的拟合程度说明该气田气流携液的临界韦伯数基本一致，因此根据式（4）可得适用于该气田的携液系数 k=2.032，结合式（5）、（6）可知该气田气流携液的临界韦伯数为1.51。

图5 LM气田环雾流临界点拟合图

3准确性验证

这里用LM气田的生产数据（不包括拟合井）对改进得到的临界携液流量计算新方法进行验证，由改进方法可得出LM气田的临界携液流量公式为：

气田生产实践表明搅动流和段塞流最早将出现在井底，积液最早在井底产生[11]。因此这里使用井底的温压条件来计算各气井的临界携液流量（见表2和图6）。

从表2及图6可以看出，利用Turner公式与Coleman公式计算LM气田的临界携液流量存在较大误差，利用李闽公式计算得到的结果虽然误差有所减小，但20组数据中仍有8组计算结果与实际不符。然而利用本文提出的新方法得到的LM气田各气井临界携液流量与实际生产数据却有着很高的吻合度，20组数据中仅有一组计算结果存在细微的偏差，说明通过本文得到的气井临界携液流量计算新方法较常规方法具有更高的准确性和现场适用性。

表1 环雾流临界点参数计算

表2 LM气田临界携液流量新老方法验证计算

图6 LM气田临界携液流量新老计算方法验证图

4 结论

（1）对临界携液流量公式中的表面张力σ和气体偏差系数Z进行了修正，并在此基础上分析了忽略σ和Z变化对临界携液流量计算的影响，分析结果表明在中压低温及高压条件下将σ和Z取为常数将带来较大的计算误差。

（2）各气田气流携液的临界韦伯数不同导致其适用的携液系数也不相同，从而造成常规临界携液流量公式不具有普遍适用性。本文提出利用气田流温流压测试数据识别环雾流临界点，再在修正表面张力和气体偏差系数的基础上利用环雾流临界点的温压条件进行反算、拟合，从而求取适用于目标气田的携液系数及临界携液流量公式。

（3）以我国西部LM气田为例，利用本文提出的新方法得到其临界携液流量公式，并用此气田的生产数据对该公式和其他常用的临界携液流量公式进行了验证和比较，验证结果表明利用本文新方法计算气井临界携液流量相较于应用常规计算公式更具准确性和现场适用性。

［1］Turner R G，Hubbard M G，Dukler A E.Analysis and Prediction of Minimum Flow Rate for the Continuous Removal of Liquids from Gas Wells［J］.Journal of Petroleum Technology，1969，21（11）：1475-1482.

［2］Coleman S B，Clay H B，McCurdy D G，et al.A New Look at Predicting Gas Well Load-up［J］.Journal of Petroleum Technology，1991，43（3）：329-333.

［3］Li Min，Sun Lei，Li Shilun，et al.New View on Continuous Removal Liquids from Gas Wells［C］.SPE 70016，2001.

［4］Luo Shu，Kelkar M，Pereyra E，et al.A New Comprehensive Model for Predicting Liquid Loading in Gas Wells［J］.Society of Petroleum Engineers，2014，29（4）：337-349.

［5］Hall K R，Yarborough L.A New Equation of State for Z-factor Calculations［J］.Oil and Gas Journal，1973，71（25）：82-92.

［6］Sutton R P.An Improved Model for Water-Hydrocarbon Surface Tension at Reservoir Conditions ［C］.SPE 124968，2009.

［7］Taitel Y，Bornea D，Dukler A E.Modelling Flow Pattern Transitions for Steady Upward Gas-liquid Flow in Vertical Tubes［J］.Aiche Journal，2010，26（3）：345-354.

［8］王志彬.气井连续携液机理［J］.石油学报，2012，33（4）：681-686.

［9］郑军，闫长辉，张文洪，等.大牛地气田气井最小携液产量研究［J］.油气地质与采收率，2011，18（1）：70-73.

［10］张耀刚，李治，于淑珍，等.靖边气田产水气井连续携液模型的优化与应用［J］.石油化工应用，2009，28（8）：77-80.

［11］Riza M F，Hasan A R，Kabir C S.A Pragmatic Approach to UnderstandingLiquid Loadingin GasWells［C］.SPE 170583，2014.