低空小型无人机雷达探测距离仿真分析
李 琴,黄卡玛
(四川大学 电子信息学院,四川 成都 610065)
0 引言
随着我国低空空域的开放[1],对无人机目标的探测与防范成为亟待解决的问题。由于无人机小RCS、低空、慢速的特点,在探测中不易被发现。目前,由于科技的迅速发展,小型化无人机发展极为迅速,无人机目标的检测与跟踪已成为一项重要的空防保卫任务。
在低空小型无人机的检测中,雷达探测距离受地杂波的干扰极为严重,文献[2-3]仿真分析了地杂波对雷达探测距离的影响。文献[4-5]对雷达杂波抑制技术进行了分析。从上述文献可知,对于地杂波背景下的雷达探测距离的分析,前人已经有了很详细的研究,但其中探测目标的RCS值均为一个假设值,且随着频率的增大,大气衰减对雷达探测距离的影响也是极为严重的。本文为更精确地分析低空小型无人机雷达探测距离,采用电磁仿真计算不同频率下无人机的RCS,然后根据在大气衰减的情况下的雷达方程,得出在不同频率下的雷达探测距离。通过对地基雷达地杂波RCS分析,得出地杂波下的雷达探测距离。最后根据MTI杂波抑制技术仿真分析了MTI杂波抑制下的雷达探测距离。将上述仿真结果进行比较得到无人机的雷达探测距离及最佳的探测频率。
1 无人机模型的RCS计算
雷达是通过对目标的散射功率进行分析来发现目标。目标的散射功率主要用RCS来描述,其定义为[6-7]:
(1)
式中,R为目标与雷达接收天线的距离;Es和Eo分别表示入射波和雷达接收到的散射波的电场强度;σ的单位为m2,而实际应用中常使用dBsm表示,转换公式为[8]:
σdBsm=10lgσm2。
(2)
本文采用电磁仿真计算无人机的RCS。建立的无人机模型如图1所示,具体参数如下:机体长度270 mm,机体宽度270 mm,机体高度160 mm,机翼长度160 mm,机翼厚度5 mm。其中浅灰色部分的材料为塑料,深灰色部分的材料为金属,黑色部分的材料为玻璃。

图1 无人机模型
本文研究的是地面雷达探测无人机目标的最大探测距离,所以将入射角度设置在目标下方,入射角范围为0°~90°,通过仿真可以得到不同频率,不同入射角下的目标RCS值,如图2所示。

图2 不同频率不同入射角下的无人机RCS
由图2可以看出,无人机的RCS是波长与入射角的函数,改变很小的角度,就会使截面积发生很大的变化。这是由于复杂反射体常常可以近似分解成许多独立的散射体,各散射体的间隔是可以与工作波长比拟的。因此当观察方向改变时,在接收机输入端收到的各单元散射信号间的相位也在变化,使其矢量相对应改变,这就形成了起伏的回波信号。至今尚无统一的标准来确定各类复杂目标截面积的单值表示值。同时从图2可以看出,不同频率下RCS值的起伏变化很难进行规律总结与分析,现在常采用各方向截面积的平均值或中值来作为截面积的单值表示[9]。本文中使用平均值表示。不同频率下所得的无人机平均RCS值如表1所示。
表1 不同频率下无人机的RCS值

频率/GHzRCS/dBsm频率/GHzRCS/dBsm1-23.580412-7.93752-20.048813-7.87073-15.014514-7.29734-14.553815-6.12305-14.899216-5.47406-12.403417-5.12097-11.956118-5.14968-11.746919-4.43409-11.821120-4.390110-10.524121-3.254511-9.080722-2.9123
2 大气衰减和地杂波影响下的雷达探测距离
2.1 雷达方程
雷达方程是探测目标信号的基本限制因素,它决定了雷达能在多远的距离上发现目标。由雷达方程得到的最大探测距离为[10-11]:
(3)
式中,Pt为雷达发射功率;Gt为雷达发射天线的增益;Gr为雷达接收天线的增益;k为玻尔兹曼常数;Te为环境温度;B为雷达带宽;L为雷达损耗;F为噪声系数;(SNR)omin为雷达探测目标所需最小输入信噪比。本文中雷达采用收发共用天线,即G=Gt=Gr,则
(4)
假设雷达天线为口径d=2 m的圆口径抛物面天线,由天线理论可知:
θA=70λ/d,
(5)
θE=Ω/θA=λ2/3283θAAe,
(6)
G=4πAe/λ2,
(7)
式中,θA和θE分别为水平和垂直的3 dB波束宽度;Ω为3 dB波束范围;Ae为雷达天线有效口径面积。假设口径效率为2/3,由上述关系可得:
(8)
2.2 大气衰减影响
当频率较大时,雷达探测距离还将受到大气衰减的影响。在低空状态下,雷达探测距离的衰减主要来自氧气和水蒸气分子的吸收损耗[12]。
在大气压强p=1 013 hpa(地面),温度t=15 ℃时,氧气分子和水蒸气分子的吸收损耗率(dB/km)分别为[13]:
(9)

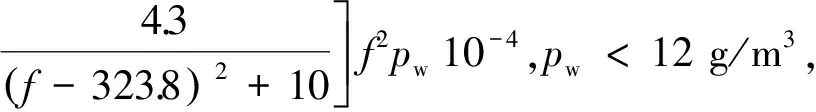
(10)
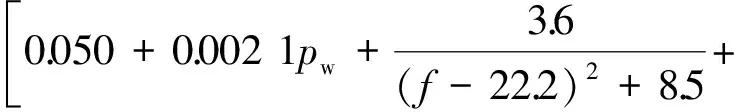
f2pw10-4,pw>12 g/m3,
(11)
式中,f为雷达频率(GHz);pw为地面水蒸气表面密度(g/m3)。
电磁波在大气中衰减的总衰减系数为:
γ=γo2+γw。
(12)
通过上述分析可以求出地面水蒸气表面密度为10.5 g/m3的大气气体吸收衰减率如图3所示。

图3 大气气体吸收衰减率
受到大气衰减影响,雷达接收功率将发生变化,这时修正的雷达方程为[14]:

(13)
由式(5)、式(6)和式(7)可得:
(14)
根据式(14)及表1所示的不同频率下的RCS值可得,当Pt=10 kW,B=100 MHz,F=3 dB,(SNR)omin=6 dB时,不同频率下由雷达方程求得的最大探测距离如表2所示。
表2 大气衰减下的最大探测距离

频率/GHz最大探测距离/m频率/GHz最大探测距离/m1214612176722371613183293607614193094719915208435804616217296997417218357109791821044811875192029891252420179121014146211514411161062212661
2.3 地杂波影响
地基雷达的杂波如图4所示[15]。其中θe为目标相对雷达视轴的夹角;θr为入射余角;hr为雷达高度;ht为目标高度;R为雷达探测距离。

图4 雷达主旁瓣杂波几何图
本文假设雷达视轴方向为目标方向,则θe=0°,那么入射角
θ>θE/2。
(15)
无地杂波影响如图5所示。

图5 无杂波区
当入射角θ<θE/2,雷达进入杂波区。假设无人机在雷达上方100 m(ht=105 m,hr=5 m)高处飞行,则杂波RCS为:
σc=σMBc+σSLc,
(16)
σMBc=σ0cRθAG2(θe+θr)secθr/2B,
(17)
σSLc=σ0cRπ(SLrms)2secθr/2B,
(18)
式中,σMBc为主瓣杂波RCS;σSLc为副瓣杂波RCS;SLrms为天线副瓣电平均方根值;G(θe+θr)为天线波束方向,假设天线波束方向服从高斯型:
(19)
σ0为杂波散射系数,为一个无量纲的标量,通常用dB表示。本文采用r-f模型描述,其公式为[16-17]:
(20)
式中,θ为入射角;V为地貌反射率表征参数;参数a、b和c均为不同地形时雷达工作频率对地形的表征参数。不同地形情况下的V、a、b和c的数值如表3所示。
表3 不同地形情况下V、a、b和c的取值

地形Vabc/(°)沙漠0.10000.080.750.50农田0.03160.180.600.55丘陵0.10000.250.201.20城市0.31600.350.180.70
因为目标与地面之间距离很大,所以此处忽略无人机和地面电磁散射干扰的耦合[18]。无人机与地面回波的信杂比(SCR)定义为:

(21)
SCR(dB)=σt(dB)-σc(dB)。
(22)
根据上述分析,可得当B=100 MHz,SLrms=-30 dB时,城市地形下不同频率不同探测距离下的信杂比如图6所示。

图6 地杂波下的信杂比
假设雷达最小可检测信杂比(SCR)omin=6 dB,由图6可以看出无人机在杂波区很难被检测。则在这时,雷达最大可探测距离为:
(23)
3 MTI杂波抑制下的雷达探测距离
目前常采用的杂波抑制方法是MTI杂波抑制技术,MTI滤波器是采用延迟线对消器来实现的,单对消器的改善因子为[19-20]:

(24)
式中,fr为雷达重复频率;σt为杂波频率的均方根值,
(25)
式中,σw为由于风速造成的杂波谱扩展的标准差;σs为由于天线扫描转动造成的杂波谱扩展的标准差;σv为由于雷达平台移动(如果有的话)造成的杂波谱扩展的标准差。可以得出:
σw=2vw/λ,
(26)
σs=0.53π/θATscan,
(27)
σv=vlsinθl/λ,
(28)
式中,vw为风速均方根值;Tscan的天线扫描时间;vl为雷达平台速度;θl为以弧度表示的相对与平台运动方向的方位角。
通过MTI杂波抑制,地杂波的杂噪比(CNR)为:
CNR′=CNR/I。
(29)
此时无人机与地面回波的SCR为:
SCR′=CNR′/SNR=Iσt/σc,
(30)
SCR′(dB)=I(dB)+σt(dB)-σc(dB)。
(31)
假设fr=1 kHz,Tscan=2 s,vw=0.45 m/s,雷达平台静止。根据上述分析可得在MTI杂波抑制下不同频率不同探测距离下的信杂比如图7所示。

图7 MTI杂波抑制下的信杂比
由雷达最小可检测信杂比(SCR)omin=6 dB可得在MTI杂波抑制的最大可探测距离如表4所示。
表4 MTI杂波抑制下的雷达最大探测距离

频率/GHz最大探测距离/m频率/GHz最大探测距离/m147711216809253311316981310225141793349112152019257999162184261070217223457109231822539811060192422791113820248341012736212750211148322228670
4 仿真结果分析
通过上述分析,可以得出不同频率下仅大气衰减影响的雷达探测距离、仅杂波影响下的雷达探测距离及MTI杂波抑制下的雷达探测距离如图8所示。

图8 不同情况下的最大探测距离
由图8可知:① 在仅考虑大气衰减和地杂波影响的情况下,无人机检测中雷达探测距离为17 362 m,雷达最佳探测频率为20 GHz;② 采用MTI杂波抑制技术,无人机检测中雷达探测距离为21 835 m,雷达最佳的探测频率为17 GHz。使用MTI杂波抑制技术,雷达探测距离可提高25.76%,且最佳的探测频率由20 GHz变为17 GHz。
5 结束语
以某无人机为参考对象计算出无人机的RCS,并仿真分析了大气衰减、地杂波及MTI杂波抑制下的雷达探测距离。结果表明在一定功率下,考虑大气衰减和地杂波的影响,最佳的探测频率为20 GHz,无人机检测中的雷达探测距离为17 362 m。进一步分析,如果采用地杂波MTI抑制技术,最佳的探测频率为16 GHz,最大探测距离为20 648 m,提高了25.76%。本文为检测低小慢目标的地基雷达设计提供参考。
[1] 董建军.“低小慢”目标的对抗措施研究[C]∥2014(第五届)中国无人机大会论文集.北京:航空工业出版社,2014:778-781
[2] 李舰,段文义,麻红.雷达地杂波建模与仿真实现[J].计算机仿真,2012,29(3):77-80.
[3] 孔庆颜,陈重,胡冰.地杂波背景中的雷达距离方程的研究[J].兵工学报,2006,27(3):442-445.
[4] 黄振远,朱琳,肖辉.X波段PD雷达杂波抑制性能分析[J].现代防御技术,2015,43(5):135-141.
[5] 焦子朋,耿哲,周思玥.MTI在连续波雷达中的应用研究[J].无线电工程,2012,42(11):62-64.
[6] HAN Yangyang,SUN Lu,HU Cong.HFSS Simulation of RCS Based on MIMO System[C]∥International Conference on Civil,Architrcture and Environmental Engineering,2017:1425-1428.
[7] 轩新想,铁煜,高喆.无人艇载光电转台基于RCS的优化选型[J].电视技术,2017,41(6):122-126.
[8] 韩红斌,刘少强.基于HFSS对目标RCS的仿真研究[J].国外电子测量技术,2015,34(3):60-63.
[9] 丁鹭飞.雷达原理[M].西安:西安电子科技大学出版社,2002:147-148.
[10] 刘庆林,夏海宝,安磊,等.地海杂波下机载预警雷达探测仿真[J].计算机仿真,2015,32(1):40-45.
[11] 刘国华.蒸发波导环境下雷达探测距离分析[J].舰船电子对抗,2014,37(5):55-58.
[12] 王海风,李皓,齐玉涛.毫米波RCS测量大气吸收衰减修正方法研究[J].科技创新与应用,2015(14):37-38.
[13] 白继玲.毫米波在大气中的传输衰减分析[D].西安:西安电子科技大学,2013:5-8.
[14] 赵秀丽,李德鑫,刘长捷.雾衰减对雷达探测距离影响分析[J].国外电子测量技术,2011,30(10):25-27.
[15] 吴阳.地面雷达低空探测杂波抑制研究[D].长沙:湖南大学,2011:11-13.
[16] 熊兴斌,王红,赵选峰,等.地杂波雷达截面积模型分析[J].火力与指挥控制,2008,33(9):79-81.
[17] 冯胜,陈杰,张娟,等.低入射余角下雷达地杂波反射率模型[J].火力与指挥控制,2005,30(2):18-21.
[18] LI Yang,TAO Ran.RCS Analysis in the Detection of a Generic Missile Tardet with Sea Clutter Background[J].Science China Earth Sciences,2014,57(11):2845-2852.
[19] 朱国富.雷达系统设计MATLAB仿真[M].北京:电子工业出版社,2009:217-220.
[20] 孙延鹏,陈晶晶,屈乐乐.基于拟牛顿法和块稀疏重建的TWR成像算法[J].计算机工程与应用,2017,53(23):212-216.

