认知星地混合网络中基于能效最大化的最优功率控制方法*

汪 晴，石盛超，边东明，朱宏鹏，唐璟宇

0 引 言

卫星通信覆盖范围广、应用场景多样，在未来的无线通信网络中扮演着越来越重要的角色。特别是在偏远地区和应急通信、救灾场合，卫星通信相较于地面系统的优越性更加明显[1]。但是，随着宽带多媒体业务的逐渐增多，卫星通信系统中频谱资源紧缺的问题愈发明显。为了解决这个问题，研究人员展开了很多切实有效的研究。其中，将认知无线电（Cognitive Radio，CR）技术[2]应用到卫星通信系统被认为是一项很有前景的工作[3]。

在众多的认知技术中，由于易于实现且可得到较高的频谱效率，underlay技术被广泛应用于各种认知无线电网络中。这种技术中，主用户可以和次级用户同时工作在同样的频段上[4-5]。但是，要使用underlay技术必须满足一个前提：次级用户的工作不会影响主用户的正常工作，即次级用户带来的干扰必须维持在一个能够接受的门限以下。所以，次级用户的功率控制问题是认知网络亟需解决的问题。当卫星系统作为次级用户系统时，文献[6-7]研究了上行链路场景下卫星用户的最优功率控制问题，其中的主用户系统分别是地面移动系统和地面固定业务系统。当卫星作为主用户系统时，文献[8]研究了在下行链路条件下，地面次级用户的功率控制问题。但是，文献[8]中的目标函数选择的是有效容量。随着绿色通信概念的产生，人们越来越关注通信系统中的环境影响和能量消耗问题[9]。文献[10]解决了通信卫星中的最佳能量分配和接入控制问题。文献[11]研究了多波束卫星中下行链路的高能效功率分配问题。但是，对于认知星地混合网络中的高能效功率控制问题，现在还很少有相关的研究工作。

正是基于以上研究背景，在认知星地混合网络场景下，当卫星系统作为主用户系统、地面移动系统作为次级用户系统时，本文针对下行链路场景中的地面次级用户，提出了两种基于能效最大化的功率控制方法。为了保证卫星用户的通信质量，使干扰功率维持在一个可以接受的门限以下，算法选取平均干扰功率（Average Interference Power，AIP）约束条件。对于次级用户的功率约束，两种算法分别选取了平均发射功率（Average Transmit Power，ATP）和峰值发射功率（Peak Transmit Power，PTP）约束。最后的仿真结果对比了两种算法的性能，分析了功率约束门限、地面干扰链路条件和卫星干扰链路条件对最终算法性能的影响，为认知星地混合网络中高能效功率分配方式提供了着实有效的指导和参考。

1 系统模型

本文研究的认知星地混合网络结构如图1所示，卫星通信系统为主用户系统，地面移动系统为次级用户系统，这里主要考虑下行链路场景，卫星用户为移动终端。关于认知技术的选择，根据前文所述，本文选择underlay的频谱共享方式。

图1 认知星地混合网络系统模型

图1 中，hp和hpi分别是卫星主用户链路和卫星干扰链路的链路增益，hs和hsi则为地面次级用户链路和次级用户干扰链路的链路增益。对于卫星链路，由于本文的卫星用户为移动终端，所以hp和hpi可以用阴影莱斯信道（Shadowed Rice Channel）进行描述[12]，即hp和hpi的概率密度函数可以表示为：

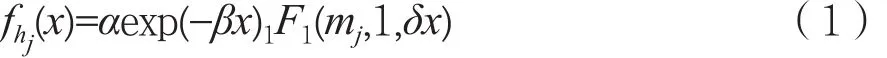
其中，j为 p 或者 pi；1F1(·,·,·)为合流超几何函数[13]，而α、β和δ可以计算：

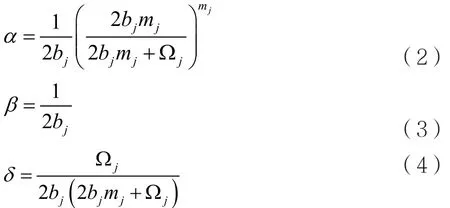
其中，2bj为散射分量的平均功率，Ωj为直射分量的平均功率，mj为Nakagami衰落因子。

至于地面链路增益hs和hsi，本文考虑Nakagami衰落信道[8]，概率密度函数为：

其中，k为s或者 si；Γ(·)为 Gamma函数[13]，mk为Nakagami衰落因子，Ωk为信号的平均功率；ε等于mk/Ωk。此外，本文假设次级用户具有理想的信道状态信息（Channel State Information，CSI）。

2 基于能效最大化的功率控制

在衰落信道场景下，能效（Energy Efficiency）通常定义为平均通信速率和平均功率消耗的比值。具体到本文研究，通过计算遍历容量（Ergodic Capacity）和平均功率消耗的比值来获得系统能效[14]。为了不影响主用户的正常工作，必须限制对次级用户造成的干扰。使用较多的两种干扰功率约束指标为平均干扰功率（Average Interference Power，AIP）约束和峰值干扰功率（Peak Interference Power，PIP）约束。根据文献[15]的研究成果：相比于PIP约束，AIP不仅可以更好地保护主用户通信质量，而且可以获得更高的通信容量。所以，本文的功率控制方案中选择AIP约束作为干扰功率的约束条件。为了进一步控制地面次级用户的发射功率，本文提出的两种功率控制方案还分别引入了平均发射功率（Average Transmit Power，ATP）约束和峰值发射功率（Peak Transmit Power，PTP）约束。

2.1 ATP约束的功率控制

ATP约束的功率控制方案中，能效最大化问题可以描述为：

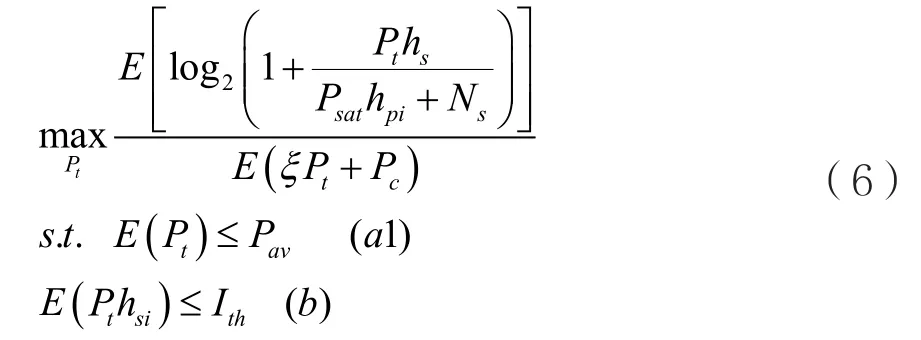
其中，Pt为地面次级用户的发射功率，Psat为卫星的发射功率，Ns为噪声功率，ξ和Pc分别表示功率放大器系数和固定环路功率损耗，E(·)代表计算期望值，Pav和Ith分别为ATP约束和AIP约束的门限值。

可以证明，式（6）是一个非线性凹的分数规划问题[16]。根据Dinkelbach’s方法[17]的结论，可以将式（6）等效为以下问题求解：

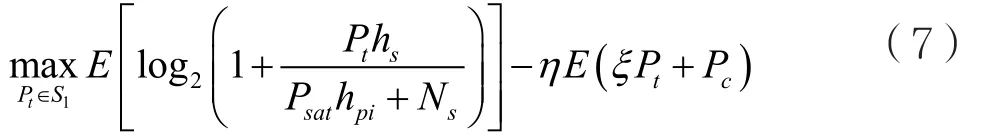
其中，η为非负参数，S1={Pt|Pt∈(a1)∩(b)}。可以证明，这是一个凸优化问题，可以通过Lagrange对偶算法进行求解[16]。

首先，写出式（7）对应的Lagrange函数：

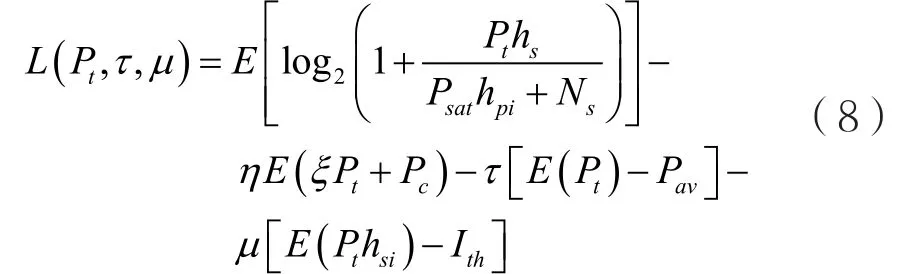
τ和μ是对应于约束条件(a1)和(b)的Lagrangian乘子，所以（7）对应的Lagrange对偶函数为：

对偶问题可以表示为：

类似于文献[15]，根据对偶分解原理[16]，问题（10）可以被分解为多个平行的子问题。这些子问题具有相同的结构，且每个子问题对应一个衰落信道状态。所以，当信道衰落状态给定后，相应的子问题可以描述为：

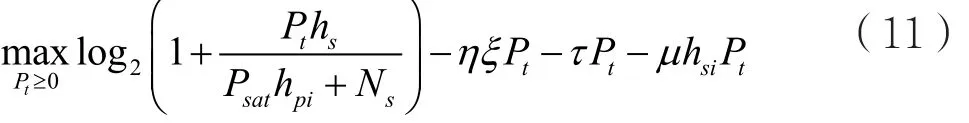
首先固定τ和μ，然后迭代求解所有衰落状态对应的子问题（11），进而利用子梯度方法[16]更新τ和μ，就可以实现求解，得到全局最优值，即式（7）对应的最优发射功率P*t为：

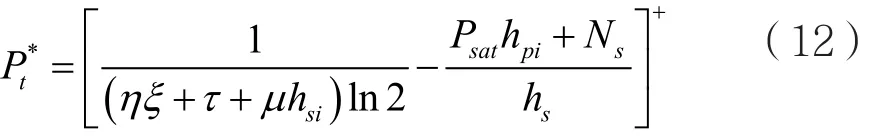
其中，[x]+=max(0,x)，表示取0和x之间的最大值。通过观察结果可以发现，只要给定η，就可以得到最优发射功率。为了进一步得到最优能效值，本文使用Dinkelbach’s方法，并在此基础上提出一种迭代功率分配方法求解式（6），得到最优能效值η*。具体的算法细节为：

设置迭代算法精度参数：ε1＞0，ε2＞0，t1＞0，t2＞0，Ni；

初始化系数：η=η0，τ=τ0，μ=μ0；

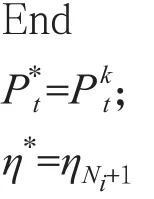
2.2 PTP约束的功率控制

当采用PTP约束时，能效最大化问题可以描述为：

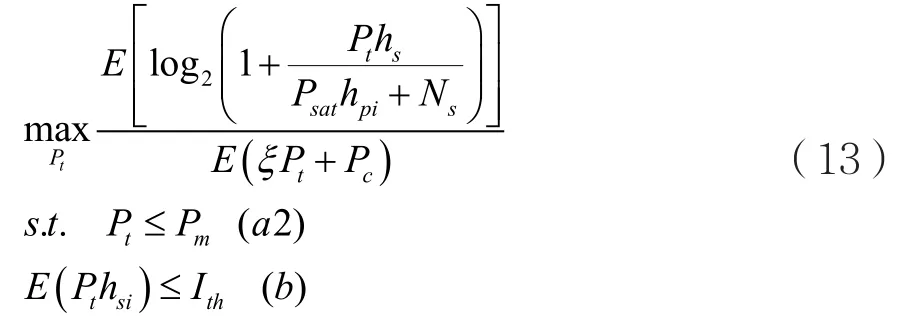
其中，Pm为PTP约束的功率门限值。问题（13）同样是一个非线性凹的分数规划问题[16]，仍然可以使用Dinkelbach’s方法进行求解。首先，得到对应的参数优化问题：

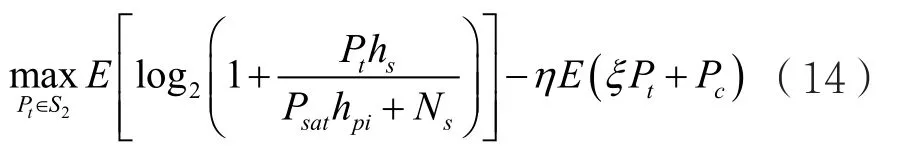
其中，S2={Pt|Pt∈(a2)∩(b)}。类似地，仍然可以使用Lagrange对偶算法式（14）进行求解。通过对偶分解后，每个衰落状态对应的子问题可以描述为：

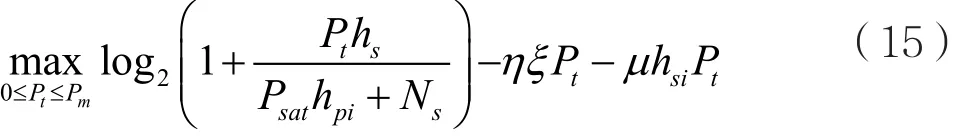
通过迭代求解所有衰落状态的子问题和结合子梯度方法来对Lagrangian乘子μ进行更新后，可以完成求解，得到发射功率：

进一步考虑式（13）中的约束条件(a2)，最终得到最优发射功率：

为了寻找求解最优能效值，仍然可以使用本文提出的迭代算法进行搜索，但要对算法进行适当修改，主要包括两点：（1）利用式（17）而不再是式（12）计算；（2）只有一个Lagrangian乘子μ需要进行更新。

3 仿真结果与讨论

这一部分将对本文提出的两种功率控制方法的性能进行仿真，并分析不同参数对最终结果的影响。仿真中使用的主要参数如表1所示，没有特别说明，这些参数将保持不变。另外，所有仿真结果都是利用Monte Carlo仿真得到，实验次数为5 000次。

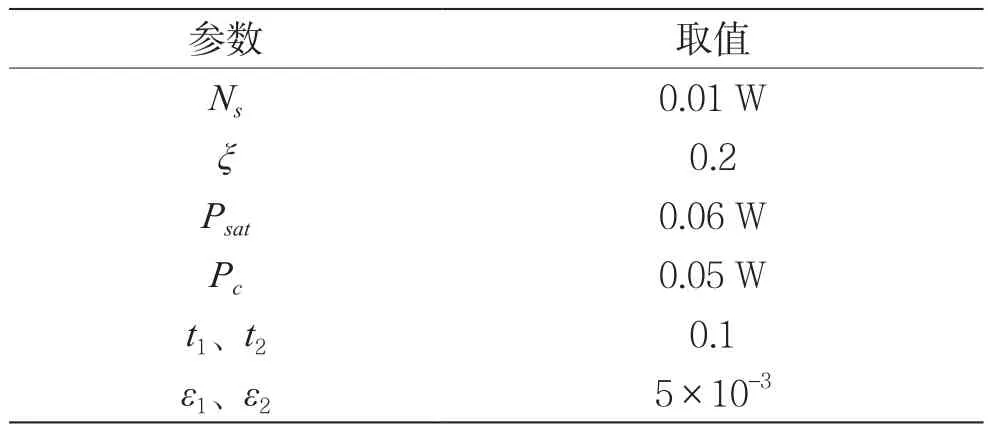
表1 主要仿真参数取值

图2给出了两种功率控制方法在不同约束指标下，次级用户能量效率随着迭代搜索算法中Ni的变化曲线。仿真中，地面信道参数取值为ms=msi=1，Ωs=1，Ωsi=0.5；卫星干扰信道参数为bpi=0.126，mpi=10.1，Ωpi=0.835[12]。仿真结果表明，两种功率控制方法不论在什么约束条件下，次级用户能效都能实现收敛，从而证明了本文所提出的迭代搜索算法的有效性；进一步观察可知，当迭代次数超过3后，最终结果就可以实现收敛，可见算法同时具有高搜索效率。

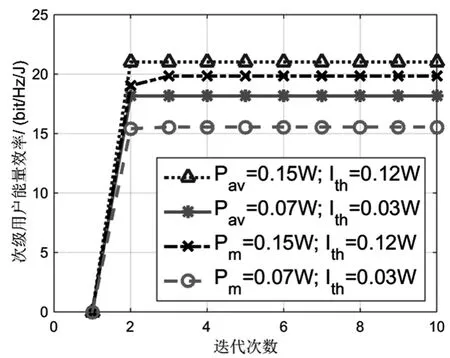
图2 次级用户能量效率随着算法迭代次数的变化曲线

图3 给出了两种功率控制方法在不同发射功率约束条件下，次级用户能效随着Ith的变化曲线，其中信道参数的取值与图2仿真所取的数值一致。结果表明，不论Pav/Pm取什么数值，使用ATP约束的功率控制方法性能总是优于使用PTP约束的功率控制方法。此外，随着Pav/Pm的提高，两种功率控制方法的性能都相应随着提升。另外，随着Ith的提高，次级用户的能效逐渐增加，进而达到一个饱和值后不再变化，这是因为在Ith较小时，对次级用户发射功率起主要约束作用的是AIP约束，但随着Ith的逐渐增大，AIP约束将不再起作用，次级用户的发射功率主要由ATP/PTP约束决定。

图3 次级用户能量效率随着Ith的变化曲线

图4 给出的是在不同的卫星干扰链路信道条件下，两种功率控制方法中次级用户能效随着Ith的变化曲线。在这个仿真里，本文选取文献[12]中的两种经典卫星衰落信道场景：Average Shadowing场景（bpi=0.126，mpi=10.1，Ωpi=0.835） 和 Infrequent Light Shadowing场 景（bpi=0.158，mpi=19.4，Ωpi=1.29）。仿真结果表明，卫星干扰链路的信道条件越好，次级用户的能效越低，即卫星干扰链路信道条件的改善不利于次级用户性能。类似地，在同样的卫星链路条件下，使用ATP约束的功率控制方法要优于使用PTP约束的方法。

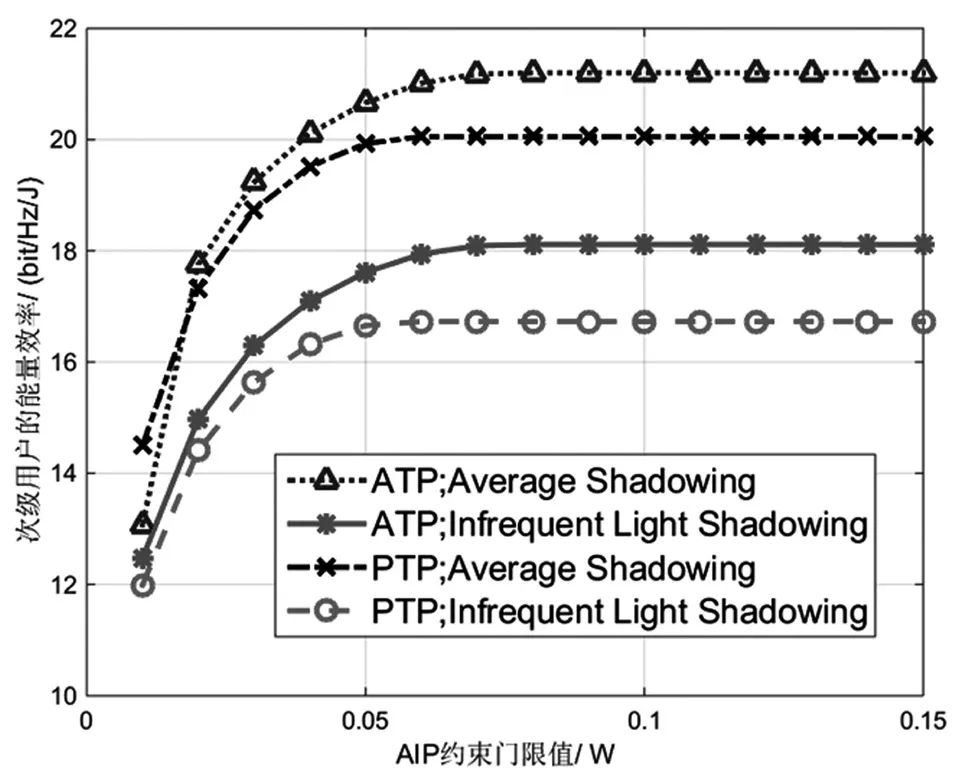
图4 不同卫星干扰链路信道条件下次级用户能效随着Ith的变化曲线

图5 给出了在不同的地面干扰链路信道条件下，两种功率控制方法中次级用户能效随着Ith的变化曲线。这个仿真中，卫星链路选择为Average Shadowing场景，Ωs=1，ms=msi=1。Ωsi越大，表示地面干扰链路的信道条件越好，对应的次级用户能效值越小，即地面干扰链路信道条件的改善同样不利于次级用户的性能。此外，在同一种功率控制方法中，不论Ωsi取什么数值，最终次级用户能效的收敛值都相同。这是因为当Ith足够大时，能效值才会收敛，而此时AIP约束已经对次级用户没有影响，这和图3得到的结论一致。

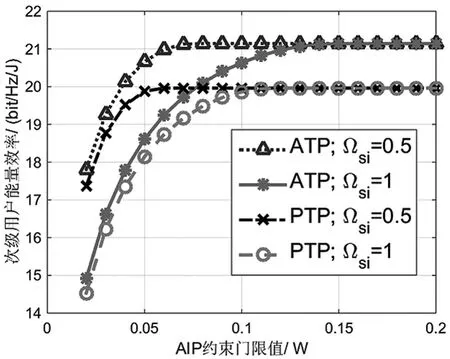
图5 不同地面干扰链路信道条件下次级用户能效随着Ithfalse的变化曲线

4 结 语

本文针对认知星地混合网络中地面次级用户的功率控制问题，提出了两种基于能效最大化的最优功率控制方法，分别选取ATP和PTP约束条件。为了保证卫星主用户的通信质量，采取AIP约束。结合Dinkelbach’s方法和Lagrange对偶方法，求解得到最优发射功率的闭合表达式，并提出了一种新的迭代搜索算法，实现了对最佳能效的高效查找。仿真结果证明，搜索算法具有有效性和高效性，并分析了功率约束门限、地面干扰链路信道条件和卫星干扰链路条件对系统最终性能的影响作用，且所得结论为认知星地混合网络中绿色通信场景下的功率控制问题提供了有效参考和指导。但是，本文的研究是在链路条件已知且理想的前提下开展的，面对非理想信道状态信息的场景，仍然需要开展进一步的研究工作。

[1] 郭庆,王振永,顾学迈.卫星通信系统[M].北京:电子工业出版社,2010:1-9.GUO Qing,WANG Zhen-yong,GU Xue-mai.Satellite Communication System[M].Beijing:Publishing House of Electronics Industry,2010:1-9.

[2] Mitola J,Maguire G Q.Cognitive Radio:Making Software Radios More Personal[J].IEEE Personal Communicatio ns,1999,6(04):13-18.

[3] Sharma S K,Chatzinotas S,Ottersten B.Cognitive Radio Techniques for Satellite Communication Systems[C].IEEE 78th Vehicular Technology Conference(VTC Fall),2013:1-5.

[4] Haykin S.Cognitive Radio:Brain-empowered Wireless Communications[J].IEEE Journal on Selected Areas in Communications,2005,23(02):201-220.

[5] Goldsmith A,Jafar S A,Maric I,et al.Breaking Spectrum Gridlock with Cognitive Radios:An Information Theoretic Perspective[J].Proceedings of the IEEE,2009,97(05):894-914.

[6] Vassaki S,Poulakis M I,Panagopoulos A D.Optimal iSINR-based Power Control for Cognitive Satellite Terrestrial Networks[J].Transactions on Emerging Telecommunications Technologies,2017,28(02):1-10.

[7] Lagunas E,Maleki S,Chatzinotas S,et al.Power and Rate Allocation in Cognitive Satellite Uplink Networks[C].IEEE ICC,2016:1-6.

[8] Vassaki S,Poulakis M I,Panagopoulos A D,et al.Power Allocation in Cognitive Satellite Terrestrial Networks with QoS Constraints[J].IEEE Communications Letters,2013,17(07):1344-1347.

[9] CHEN Y,ZHANG S,XU S,et al.Fundamental Trade-offs on Green Wireless Networks[J].IEEE Communications Magazine,2011,49(06):30-37.

[10] FU A C,Modiano E,Tsitsklis J N.Optimal Energy Allocation and Admission Control for Communications Satellites[J].IEEE/ACM Transactions on Networking,2003,11(03):488-500.

[11] Qi T,WANG Y.Energy-efficient Power Allocation over Multibeam Satellite Downlinks with Imperfect CSI[C].IEEE WCSP,2015:1-5.

[12] Abdi A,Lau W C,Alouini M S,et al.A New Simple Model for Land Mobile Satellite Channels:First-and Secondorder Statistics[J].IEEE Transactions on Wireless Comm unications,2003,2(03):519-528.

[13] Gradshtevn I S,Ryzhik I M.Table of Integrals,Series,and Products[M].Seventh Edition.Elsevier,2007:820.

[14] WANG L,SHENG M,WANG X,et al.Mean Energy Efficiency Maximization in Cognitive Radio Channels with PU Outage Constraint[J].IEEE Communications Letters,2015,19(02):287-290.

[15] ZHANG R.On Peak Versus Average Interference Power Constraints for Protecting Primary Users in Cognitive Radio Networks[J].IEEE Transactions on Wireless Comm unications,2009,8(04):2112-2120.

[16] Boyd S,Vandenberghe L.Convex Optimization[M].Cambridge:Cambridge University Press,2004:127-129.

[17] Dinkelbach W.On Nonlinear Fractional Programming[J].Management Science,1967,13(07):492-498.