基于ARIMA与GM(1,1)的区域用水总量预测模型及应用
——以广州市为例
田 涛,薛惠锋,张 峰
(中国航天系统科学与工程研究院,北京 100048)
水资源作为生产生活的重要基础资源,其使用量直接反映了国家或地区的经济发展和人民生活的质量水平,而受国内水资源分布及社会经济发展等多种因素的影响,水资源污染、短缺等问题愈发严重。对此,国家水资源管理中专门设定了“三条红线”,明确将用水总量控制作为其重要组成内容,同时也是水行政主管部门的主要考核指标之一。区域用水总量主要是指在一定时期内(月、季度、年),一个国家或地区的工业、农业、生活、生态等的用水总和,是衡量该区域对水资源开发利用程度的重要指标[1]。在最严格水资源管理制度规定下,广东省是全国唯一一个到2030年用水总量控制红线下降的省,即广东省要在保持经济稳定发展的基础上进一步控制用水总量,这对广东省用水资源管理工作带来极大的挑战。因此,提高其用水总量预测水平具有重要的现实意义。
随着各类预测模型应用的愈加广泛,目前对用水总量预测已成为水资源管理研究的热点。Yadav等采用小波与支持向量机的方法建立了水资源消耗预测模型,实现了对水资源消耗数据滤波处理与多指标预测目标[2];Eslamian等从日用水量需求的角度提出水资源使用量的多元线性回归模型,并发现模型的拟合精度关键在于回归参数的选择[3];Qaderi等利用小波函数优化BP神经网络,以此克服传统BP神经网络中的局部收敛弊端,并用其建立区域用水预测模型[4];Sempewo等运用马尔可夫链建立水质预测模型,通过水质区间的划分建立空间状态转移矩阵[5]。国内学者袁朝阳等基于集对分析聚类方法对山东省用水总量进行了静态预测[6];孙艳等针对传统粒子群算法在用水量预测上的不足,选取自适应变异粒子算法对其改进,并在农业用水中进行了精度验证[7];刘秀丽等认为用水总量的预测可从其影响因素的视角进行多属性关联性分析,并据此建立了用水总量的多因素预测模型[8];佟长福等选取定额法与增长比率法相结合的方式对鄂尔多斯工业用水趋势进行了预估[9]。此外,还有学者使用恩格尔系数[10]、贝叶斯神经网络[11,12]、遗传算法[13]等进行用水总量预测研究。
综上所述,现有相关研究成果从多维度对用水量预测进行了探讨,尤其是针对其适用性模型选择与构建方面,为水资源数据分析与管理决策提供了重要借鉴。但实际上影响区域用水状态的因素复杂多样,并呈现较强的非线性和时序变化特性,其内部变化因素较难用标准模型进行描述,因此从时间序列角度对区域用水总量进行定量分析和预测具有一定的客观性,与此同时,基于不同的用水样本数据,其适用性的预测方法还有待进一步挖掘。据此,本文以广州市2002-2016年用水总量数据为例,根据其年用水总量随时间变化的特点分别构建基于自回归移动平均模型(Auto-regressive Integrated Moving Average Model,ARIMA)和灰色GM(1,1)区域用水总量预测模型,并对广州市用水总量进行预测,并比较不同模型对于用水总量预测的准确性,为其用水总量控制提供理论与方法参考。
1 数据来源与模型构建
1.1 研究区概况与数据来源
广州市位于东经112°57′-114°3′,北纬22°26′-23°56′,地处广东省中南部(见图1),并作为广东省省会,是中国特大城市之一,属于亚热带沿海地带,其境内流域隶属珠江水系。全市2016年降雨量达到176.8 亿m3,水资源总量102.9 亿m3,虽然从规模上看其总量相对丰富,但由于快速增长的经济和庞大的人口规模使其人均水资源量偏低,仅为747 m3,而多年平均值为549 m3,均显著低于广东全省的2 251和1 675 m3,而人均综合用水量(469 m3)明显高于全省平均水平(398 m3),可利用淡水资源也愈发紧张[14]。可见实现广州市的用水总量控制是缓解水资源供需矛盾的关键。
图1 广州空间地理位置
本文采用的水资源总量数据样本区间为2002-2016年,主要来源于《广州市水资源公报》,2016年数据来源于《2016广州市国民经济和社会发展统计公报》。
1.2 模型构建
1.2 1 ARIMA模型
ARIMA模型是由Box和Jenkins在20世纪70年代提出的时间序列预测方法,又称Box-Jenkins模型[15]。该模型将时间序列数据作为随机过程,并通过特定的数学模型将其定量化模拟,可有效描述时序数据的动态性与持续性特征,尤其是在解决非平稳时间序列数据问题上已得到了较好的验证[16]。考虑用水总量时间序列的变化受到社会经济发展及节水技术等多方面复杂因素的影响,具有典型的非平稳时序数据特征,因此,可尝试采用该模型对其变化趋势进行预测分析。在ARIMA模型中,ARIMA(p,d,q)称为差分自回归移动平均模型,其中,AR是自回归,p是自回归项,MA表示移动平均,q为移动平均项数,d为使时间序列成为平稳所做的差分次数[17]。
对于用水总量时间序列xt,若能通过d次差分有变成平稳序列,即xt~I(d),则有:
zt=Δdxt=(1-B)dxt
(1)
zt为平稳序列,由此可建立ARMA(p,q)模型:
zt=c+φ1zt-1+…+φpzt-p+εt+θ1εt-1+…+θqεt-q
(2)
通过d阶差分后的ARMA(p,q)模型成为ARIMA(p,d,q)模型,εt表示白噪声过程。
1.2.2 GM(1,1)模型
灰色理论是邓聚龙教授于1982年提出的一种用于处理既含有已知信息又含有未知或非确定信息问题的方法,据其理论可对建立不同的灰色微分预测模型,并对特定指标数据未来状态做出相对合理的定量预测[18]。其中,GM(1,1)是灰色理论建模中最典型及应用范围最广的模型之一,由包含单变量的一阶微分方程构成[19]。设用水总量时间序列:
x(0)=[x(0)(1),x(0)(2), …,x(0)(n)]
(3)
灰色模块微分方程:
(4)
将灰参数代入时间函数,取得:
(5)
根据累加序列的预测结果进行运算,得出原始序列的预测值:
(6)
1.2.3 模型有效性检验
按照区域用水总量预测的模型拟合精度要求,本文选用平均绝对误差与平均相对误差对ARIMA(p,d,q)和GM(1,1)模型检验其在用水总量预测上的应用效果[20,21]。公式如下。
(1)平均绝对误差:
(7)
(2)平均相对误差:
(8)
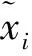
2 实证分析
2.1 模拟预测及结果对比
(1)ARIMA模拟预测。根据广州市2002-2016年历史用水总量时序统计数据xt,可观测出全市用水总量整体上呈现出相对显著的逐年下降趋势(见图1),并属于非平稳序列。为消除其时间序列趋势,对用水总量原始序列做一阶差分处理,记为Dxt,可发现该处理后的数据序列相对稳定,即序列趋于平稳。为进一步验证其结果的可信性,本文选用ADF和PP单位根检验验证上述序列的平稳状况,结果见表1。
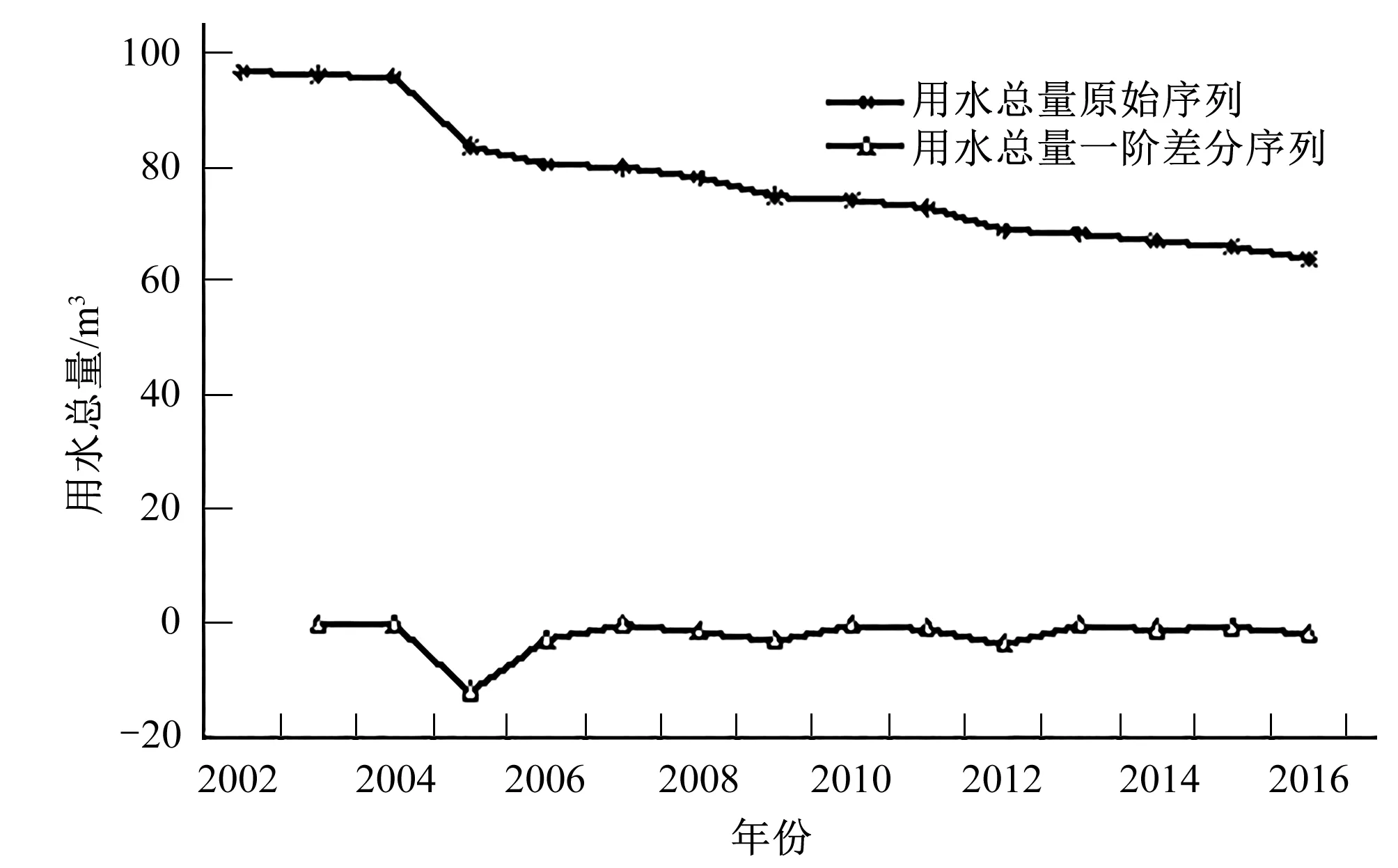
图2 广州市2002-2016年用水总量原始序列及一阶差分序列
通过表1可知,用水总量原始数据序列在一阶差分后的序列Dxt进行ADF与PP检验时,在各检验水平下均低于其临界值,而此可视为用水总量一阶差分序列Dxt在99%的置信水平下满足上述检验要求,属于平稳时间序列。
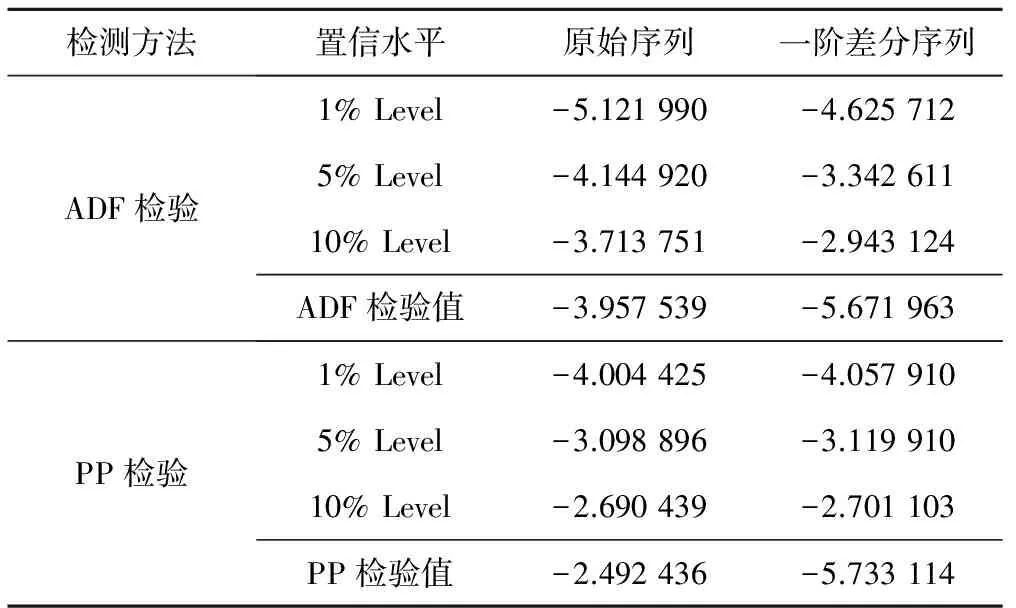
表1 单位根检验结果
基于上述平稳性检验,利用ARIMA模型检验时需要进行自相关与偏自相关分析,对原始用水总量序列 再次进行验证时,其序列自相关系数(AC)和偏相关系数(PAC)表现出非拖尾特征(见图3),这进一步印证了表1中的检验结果。而对用水总量一阶差分序列 的检验(见图4)则表明AC和PAC属于拖尾特性,并呈几何递减趋势。由此可判定ARIMA(p,d,q)的p和q为1,同时通过白噪声序列检验确定其d=1。因此,最终确定模型为ARIMA(1,1,1),对此可使用Eviews软件对广州市用水总量进行拟合。
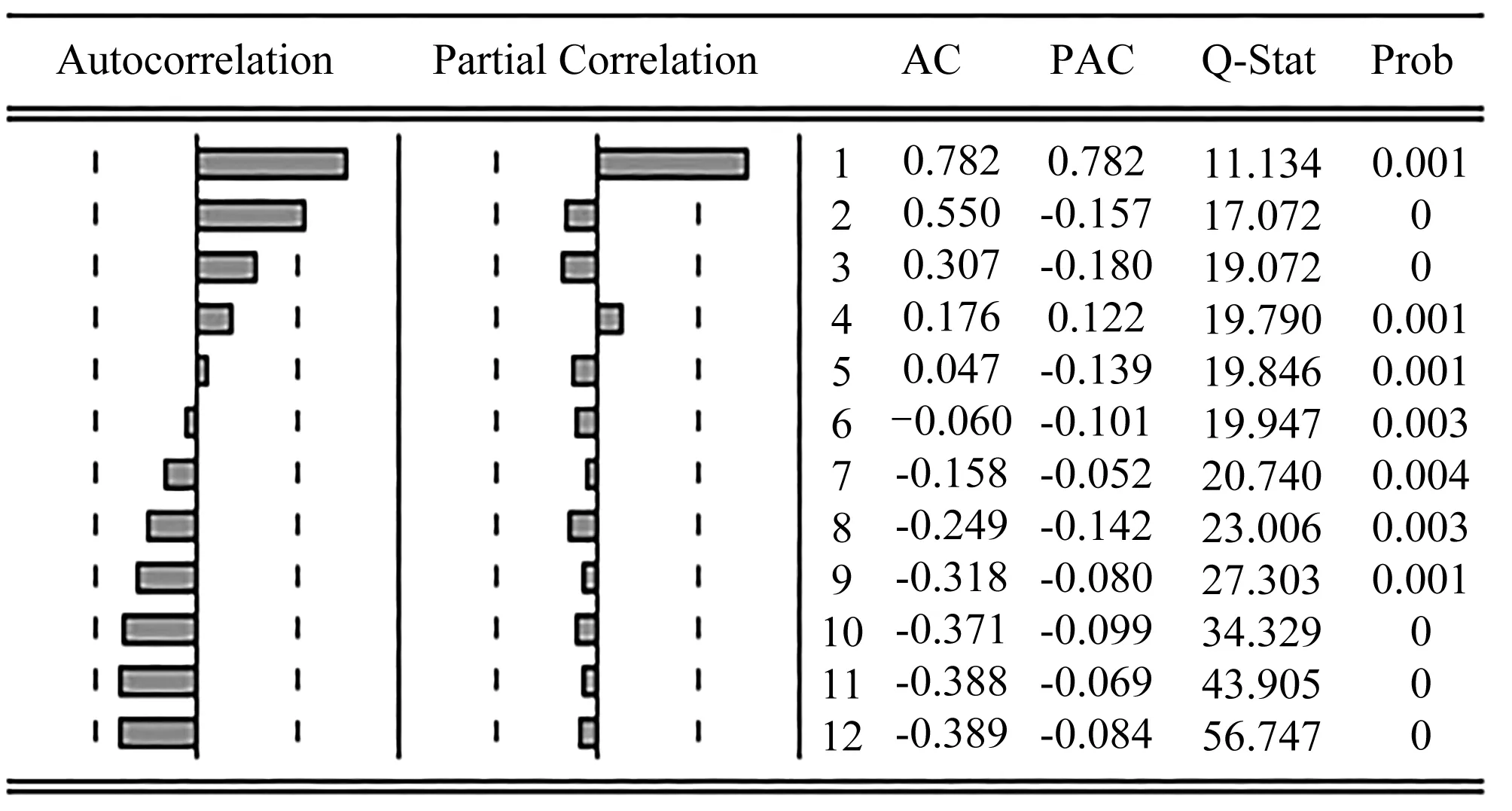
图3 用水总量时序自相关-偏自相关检验结果
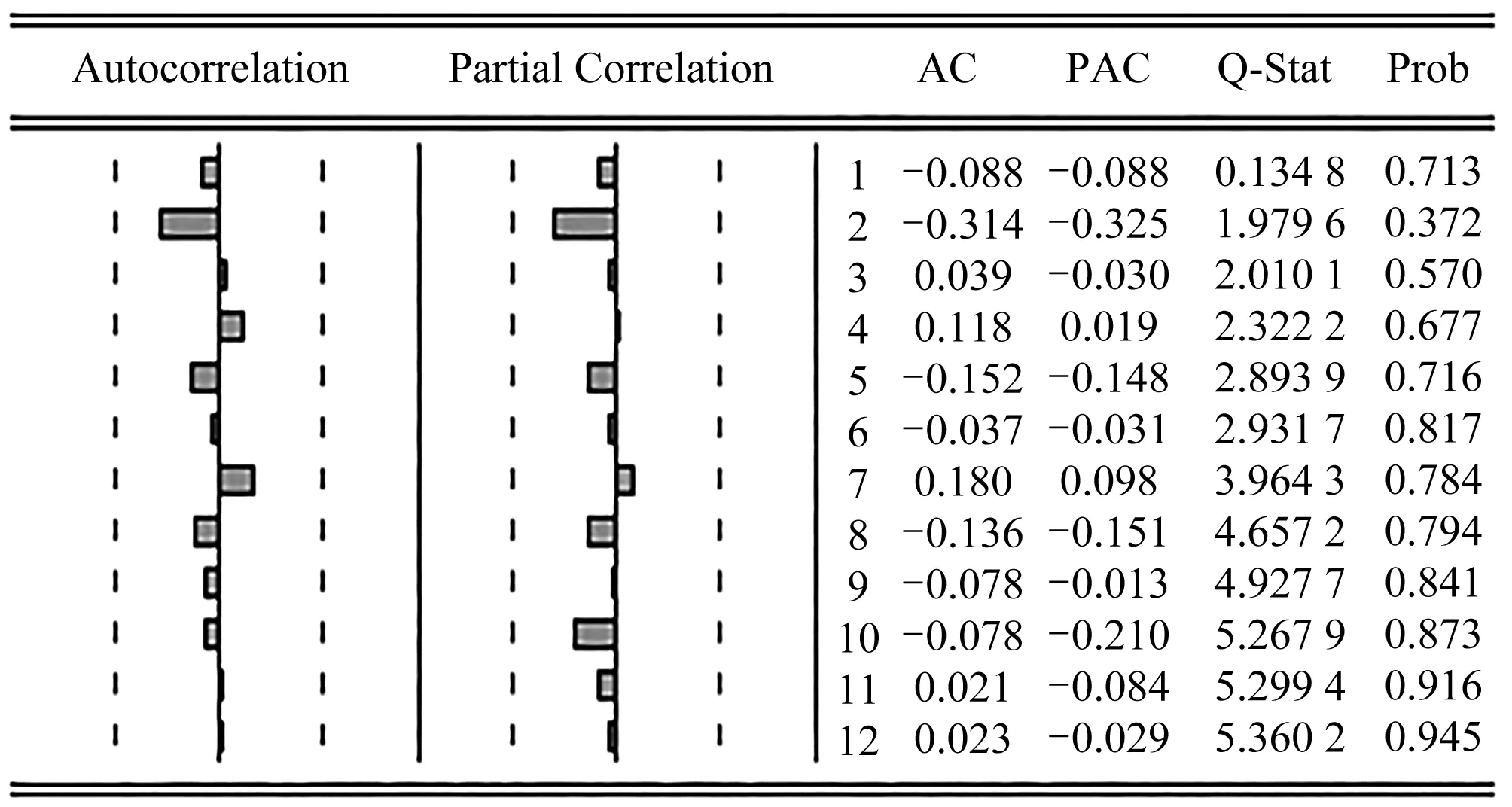
图4 用水总量时序一节差分自相关-偏自相关检验结果
进行参数估计之后模型建立为:
zt=-1.918 366+0.617 619zt+1+εt-0.999 160εt-1
(9)
(2)GM(1,1)模拟预测。按照GM(1,1)模型的测算过程,利用MATLAB软件编程计算模拟产生序列如下:
(10)
原始序列预测模型:
95.872 8 e-0.031 0 k
(11)
(3)模拟预测结果对比。根据上述各模型测算结果,分别运用模型(9)和(11)模拟预测2002-2016年广州市水资源用水总量,其模拟预测结果及误差见表2和图5。
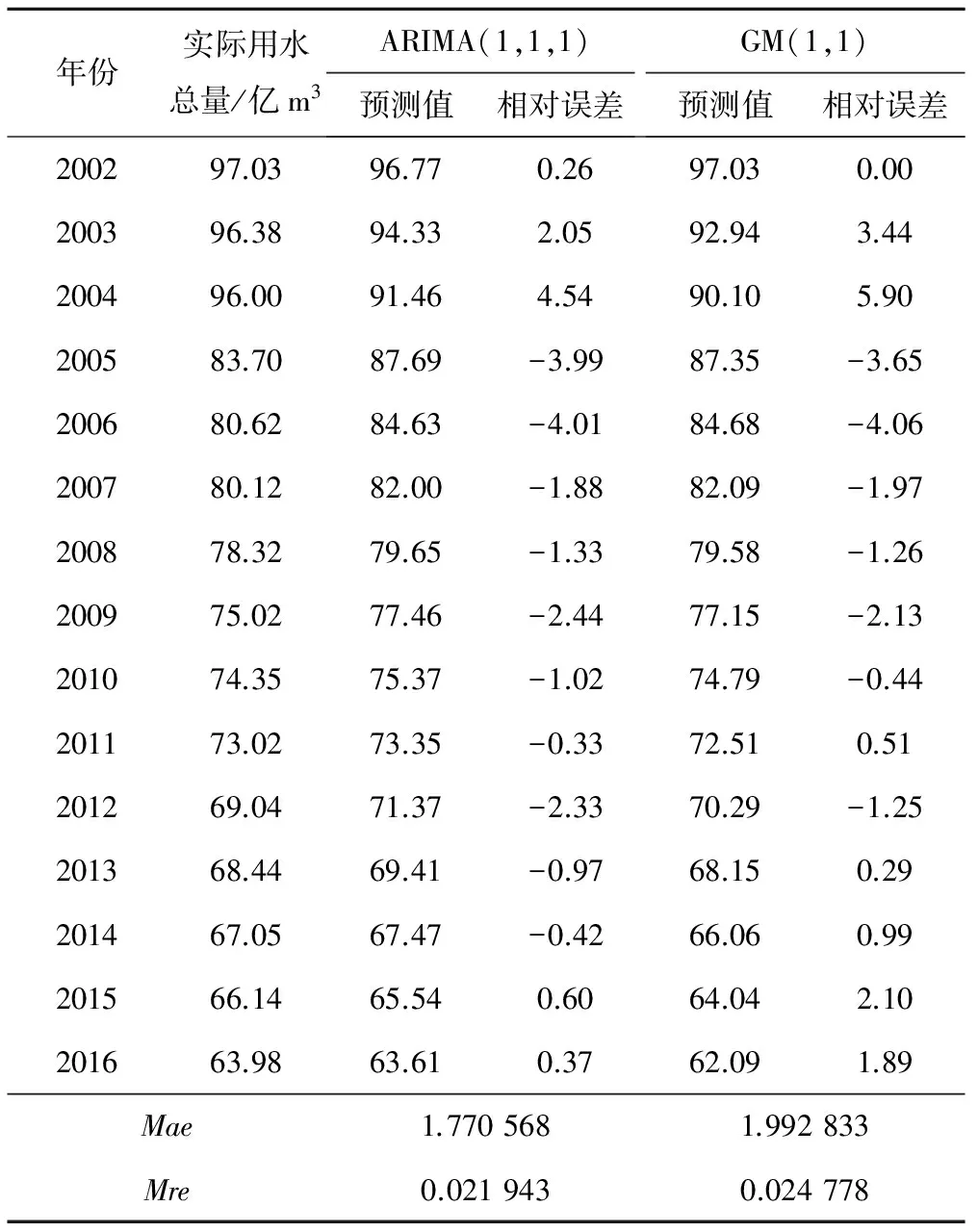
表2 ARIMA(1,1,1)和GM(1,1)模型预测结果
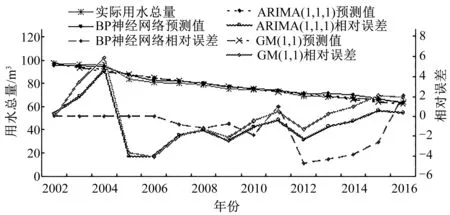
图5 2002-2016年广州市年用水总量变化曲线
按照表2与图4所示模拟预测结果,可以发现两类模型除了在局部年份下具有显著性的误差以外,均在整体上表现出了相对较好的拟合精度,但是对比两类模型相对误差大小时,则可进一步发现ARIMA(1,1,1)的相对误差在总体趋势上表现为逐步降低并收敛的态势,且误差除2004-2006年以外,其余均控制于±3以内;而GM(1,1)模型拟合相对误差则在总体上表现为先收敛后发散的变动趋势,即拟合初期相对误差较高,尤其是在2004年时更是突破了相对误差为5的临界值,而后期呈现为下降的态势,并于2006-2008年期间相对误差与ARIMA(1,1,1)模型差异较小,但在拟合后期(2015-2016年)则又出现了较大程度的波动。同时,对比两者的平均绝对误差(Mae)和平均相对误差(Mre),ARIMA(1,1,1)模型要低于GM(1,1)模型,这说明前者的模拟效果要强于GM(1,1)模型。
此外,观测ARIMA(1,1,1)和GM(1,1)模型在数据样本模拟区间内的各年份下拟合值,通过对比用水总量实际值可知两类模型在多数情况下均出现了“同向拟合过度或不足”的现象,即在同一年份下拟合值均同时低于或同时高于实际值,说明两类模型并不适合做加权组合预测模型。据此,本文选用ARIMA(1,1,1)模型对广州市用水总量趋势进行预测分析。
2.2 用水总量变化趋势预测
参考广州市2016-2020年最严格水资源管理制度中对全市划定的时间节点,本文将用水总量变化趋势预测的规划年份定于2020年。利用ARIMA(1,1,1)模型对广州市2017-2020年用水总量进行预测,结果见表3和图6所示。
根据预测结果,可知广州市若按照现阶段的用水态势,其在未来的4 a内用水总量将保持较为显著的下降态势,尤其是在2018-2020年期间,其用水下降速率相对稳定,并到2020年时,其用水总量可控制在56 亿m3的水平。
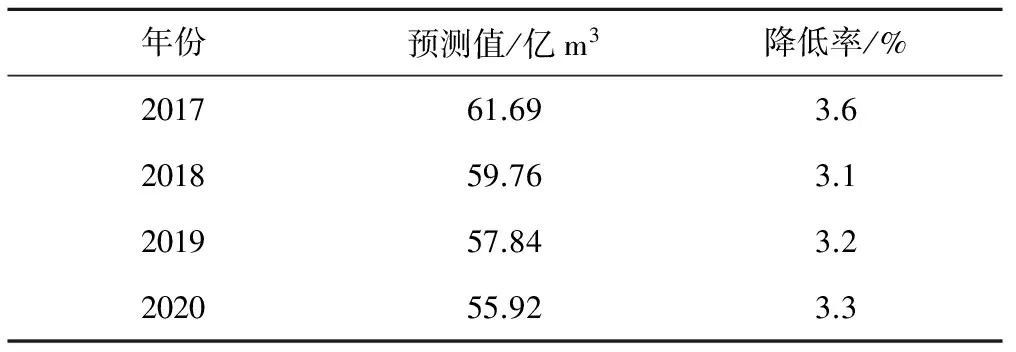
表3 广州市用水总量2017-2020年预测结果
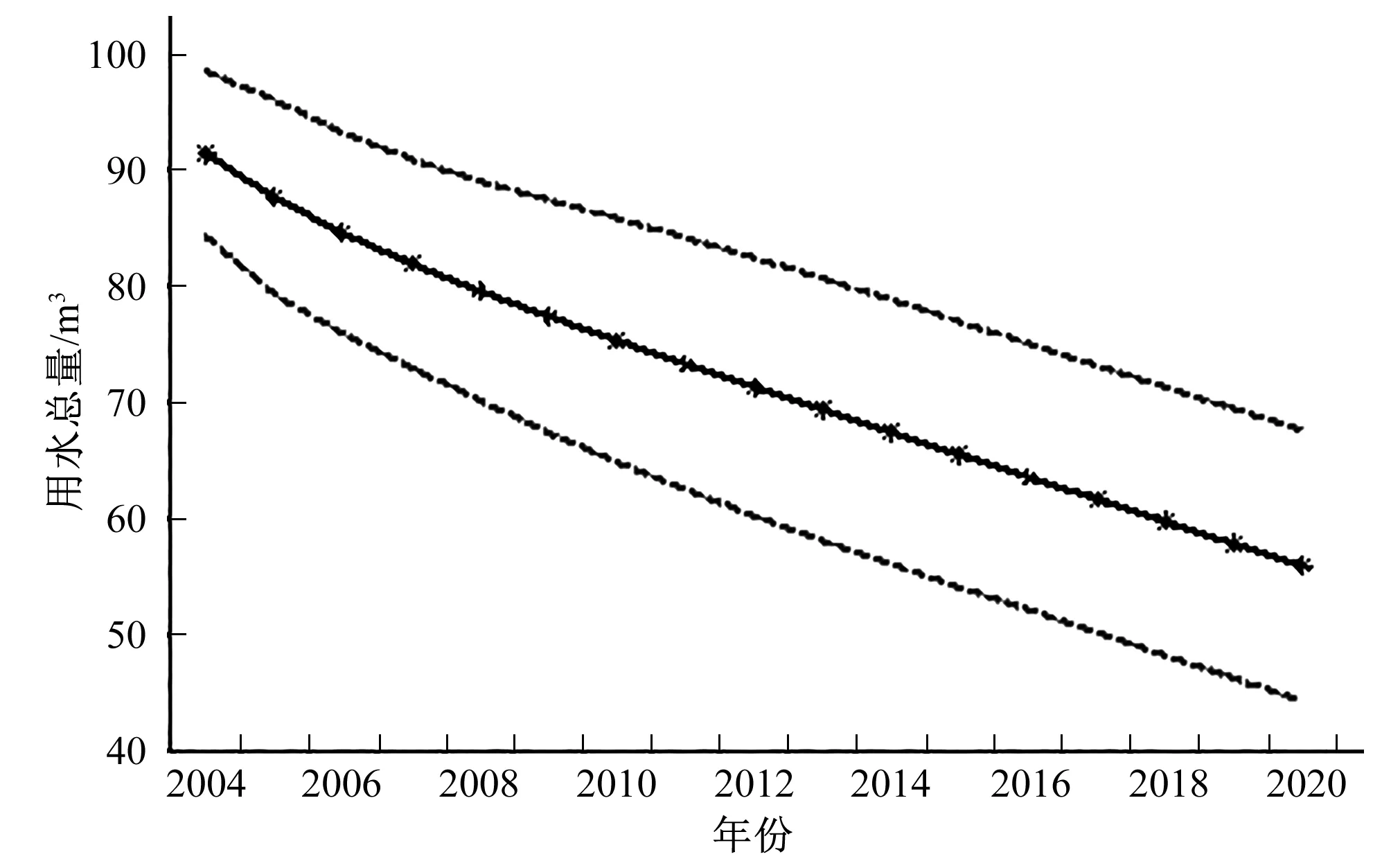
图6 广州市年用水总量预测图
3 结果讨论
自2012年全国开始实行最严格水资源管理制度开始,全国各地区对用水总量进行严格控制,广州市从2012年开始用水总降低率趋于平稳,并稳定在3%左右,而从本文对其全省用水总量的预测情况(见表3),可知未来到2020年用水总量降低率也较为平稳。这说明近年来广州市在用水总量控制上所实施的政策措施较为有效,且在“十三五”期间全市用水总量控制水平稳定,同广州市“水利十三五规划”总体要求可保持相对一致。而在全市用水总量整体变化趋势呈稳定下降的态势下,广州市到2020年划定用水总量红线为49.52 亿m3,但是从本文的预测值(55.92 亿m3)来看,如果按照现有年降低率,广州市到2020年应对用水总量红线指标将面临严峻挑战。
水资源是社会经济发展的重要支撑性资源,其使用量变化与经济增长情况具有紧密相关性。而对比观测广州市经济增长与水资源使用量的变化(见表4),可进一步发现农业用水量与农业生产总值之间在数值波动上基本一致,但若从变量的增长率比较中,则存在非同步现象。农业用水量为“先降后增”的趋势,而农业生产总值则为“先增后降再增”的特点。同样的非同步现象出现于工业用水量与其生产总值的增长率对比之间,即工业用水量为“先增后降再增”,而其生产总值则是“先将后增再降”的趋势。导致上述问题的因素有多种,其中既有自然资源的不确定性因素影响,也有涉水政策的宏观调控及节水技术、工艺、设备使用等,但在推进社会经济稳定发现的前提下,实现用水总量的控制则需要对其增长率进行严格调控,从该方面来看广州市仍有较大节水潜力进行挖掘。
此外,通过统计广州市2011-2015年用水总量构成结构变化(见表4),可知全市虽然生态与生活用水量虽然随着社会经济水平的提高,其总体上呈现出上升态势,但从所占比率来看工业和农业用水量依然是用水消耗的主要对象。而且在此期间,生活用水量在整体上保持相对稳定的变化,而工业用水总量呈上升趋势,农业用水并未因灌溉技术升级等因素而出现明显降低。所以,在“十三五”中后期,广州市应该以“加快农业灌溉技术水平提升,重点解决工业用水的用水效率”为用水调控主线,降低万元GDP增加值的工业用水量,同时强化农业用水过程中的节水管控力度,从而保障其完成控制用水红线的基本目标。
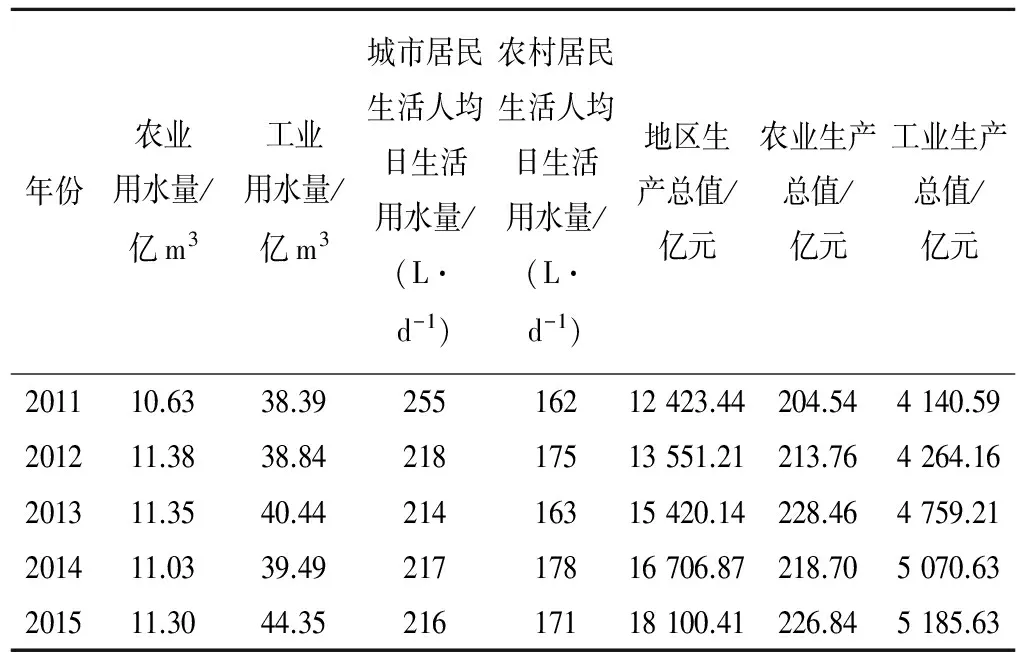
表4 广州市2011-2015年工业、农业用水量
4 结 语
本文利用ARMA和灰色理论分别构建区域用水总量预测模型,并以广州市用水总量2002-2016年历史数据为样本对模型的有效性进行对比,结果基于现有数据条件下:
(1)ARIMA(1,1,1)模型较灰色GM(1,1)模型更适用于用水总量的预测,其平均绝对误差与相对误差较低,而在样本拟合预测中,ARIMA(1,1,1)模型相对误差表现出了稳定收敛下降的趋势,灰色GM(1,1)模型则呈现为先收敛后发散的误差变动特点,进一步说明ARIMA(1,1,1)模型预测精度更为理想。而将模型的模拟预测与实际值比较,发现两类模型均具有“同向拟合过度或不足”的现象,即不适用于进行加权组合进行用水总量预测。
(2)选取ARIMA(1,1,1)模型模拟预测中发现,广州市自实行最严格水资源管理制度后其用水总量具有平稳下降的特点,但全市2020年用水总量将达到55.92 亿m3,同比广州市划定的2020年用水总量红线相比高出6.4 亿m3,说明在用水总量处于稳定下降的态势下,其用水总量红线控制风险依然较高,需要在未来4 a内加大用水总量控制力度。
(3)结合ARIMA(1,1,1)模型预测结果,进一步分析2011-2015年广州市农业、工业用水总量等变化情况,发现工业和农业用水分别与其生产总值之间的增长率变化存在非同步现象,而在以2020年广州市达到用水总量红线指标要求的前提下,全市在“十三五”中后期亟需加大工业用水效率,通过应用先进的节水技术、工艺和设备等进一步降低万元工业产值用水量,同时提高农业灌溉技术的研发与投入使用力度以控制农业用水量,从而实现对用水总量的严格控制。
[1] 张玲玲,王宗志,李晓惠,等.总量控制约束下区域用水结构调控策略及动态模拟[J].长江流域资源与环境,2015, 24(1):90-96.
[2] Yadav B, Eliza K. A hybrid wavelet-support vector machine model for prediction of Lake water level fluctuations using hydro-meteorological data[J]. Measurement, 2017,(103):294-301.
[3] Eslamian S A, Li S S, Haghighat F. A new multiple regression model for predictions of urban water use[J]. Sustainable Cities and Society, 2016,(27):419-429.
[4] Qaderi F, Babanejad E. Prediction of the groundwater remediation costs for drinking use based on quality of water resource, using artificial neural network[J]. Journal of Cleaner Production, 2017,(161):840-849.
[5] Sempewo J I, Kyokaali L. Prediction of the future condition of a water distribution network using a markov based approach: a case study of kampala water[J]. Procedia Engineering, 2016,(154):374-383.
[6] 袁朝阳,吴成国,张礼兵,等.集对分析聚类预测法在区域用水量中的应用[J].华北水利水电大学学报(自然科学版), 2015,36(4): 32-35.
[7] 孙 艳,刀海娅.自适应变异粒子群算法与支持向量机在农业用水预测中的应用[J].水资源与水工程学报,2015,(3):231-236.
[8] 刘秀丽,邹庆荣.我国用水总量预测研究[J].系统科学与数学,2016,36(10):1 643-1 651.
[9] 佟长福,史海滨,李和平,等.鄂尔多斯市工业用水变化趋势和需水量预测研究[J].干旱区资源与环境,2011,25(1):148-150.
[10] 张志果,邵益生,徐宗学.基于恩格尔系数与霍夫曼系数的城市需水量预测[J].水利学报,2010,41(11):1 304-1 309.
[11] 占 敏,薛惠锋,王海宁,等.贝叶斯神经网络在城市短期用水预测中的应用[J].南水北调与水利科技,2017,15(3):73-79.
[12] Wu J, Xu S, Zhou R, et al. Scenario analysis of mine water inrush hazard using Bayesian networks[J]. Safety science, 2016,(89):231-239.
[13] Shin H, Joo C, Koo J. Optimal rehabilitation model for water pipeline systems with genetic algorithm[J]. Procedia Engineering, 2016,(154):384-390.
[14] 张 静,余鹏翼,刘 娜.基于广州市水资源供需平衡分析的实证研究[J].生态经济(学术版), 2010,(1):322-325.
[15] Calheiros R N, Masoumi E, Ranjan R, et al. Workload prediction using ARIMA model and its impact on cloud applications’ QoS[J]. IEEE Transactions on Cloud Computing, 2015,3(4):449-458.
[16] 张 潇,夏自强,黄 峰,等.基于SSA-ARIMA模型的青弋江干流径流预测[J].中国农村水利水电,2015,(3):6-9.
[17] 王 耕,王嘉丽,苏柏灵.基于ARIMA模型的辽河流域生态足迹动态模拟与预测[J].生态环境学报,2013,(4):632-638.
[18] 邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990:14-18.
[19] Zhao H, Guo S. An optimized grey model for annual power load forecasting[J]. Energy,2016,(107):272-286.
[20] 董承秀,陈继光.波动水资源数据灰幂模型预测中的维数选择[J].节水灌溉,2015,(2):61-62.

