基于健康江湖关系的长江中游库群多目标优化调度研究

苏律文，杨 侃，邓丽丽

(1.河海大学水文水资源学院，江苏 南京 210098；2.太湖流域管理局水文局(信息中心)，上海 200434)

与长江有着十分密切江湖关系的洞庭湖和鄱阳湖，是我国最大的两个淡水湖泊。长江中游水库(三峡水库、洞庭湖流域水库和鄱阳湖流域水库)的建成与运行给人类带来了巨大的经济效益，但同时也在一定程度上影响了库区和长江中游的生态系统环境。特别是三峡水利枢纽的建成与运行，显著改变了长江中游的水文情势，对位于长江中游的洞庭湖和鄱阳湖等通江湖泊的生态系统环境将有一定程度的影响。长江中游水库(三峡水库、洞庭湖流域水库和鄱阳湖流域水库)的蓄水期大部分在每年的10月份，水库下泄流量的削减，将使洞庭湖代表站城陵矶的水位下降1m左右，导致部分洲滩提早显露水面，暴露的滩地加快失水，明显部分植物的生长产生影响，天鹅、白鹤等的越冬饵料和栖身地面积将缩减[1,2]。同时，长江干流下泄流量的减少将削弱长江对鄱阳湖的顶托作用，鄱阳湖湖口出流速度加快，鄱阳湖水位下降，导致洲滩提早露出水面，将减少水禽栖身洼地的水面面积，能够食用的饵料削减，人类加剧干扰候鸟栖身地，水禽和候鸟的正常越冬生活受到影响[2,3]。

因此，水库工程的建设与运行对两湖地区的生态环境系统造成了一定的影响。可是目前的水库运行调度方式更多的是追求经济效益，很少考虑两湖的生态环境，严重影响了两湖地区生态环境的健康发展。考虑到两湖生态系统健康发展的需要，水库运行管理不再是一个孤立的简单调度问题，水库运行调度正朝着多层次、多目标、多尺度方向发展，其优化运行目标从单目标、单一时空标准改变成可变时空标准下多目标综合效益的最优。从20世纪90年代开始，以进化算法为代表的现代智能优化算法逐渐在水库群优化调度中得到广泛的关注与应用。目前主要的优化算法有遗传算法、粒子群算法、蜂群算法、蚁群算法等，其中遗传算法应用较广，但其存在算法早熟等缺点。带有权重系数的粒子群算法寻找最优解时优越性较强[4]，但在Shu-Chuan Chu的研究中发现，猫群算法比粒子群算法具有更优的性能[5]。Tsai等[6]把猫群算法与人工蜂群算法进行混合优化，通过5种基准函数的测试证明了该算法在精确性、快速性、收敛性及稳定性方面表现良好。Pradhan等[7]首次将猫群算法应用于求解多目标问题，与MOPSO和NSGA-II相比，多目标猫群算法更接近Pareto最优边界并能更好的搜索到全局最优解。

本文根据长江中游实际情况，建立了基于主观偏好和改进熵权的Vague集多属性决策方法，分析不同主观偏好情况下的调度方案，并采用改进猫群算法对模型进行高效求解。目前猫群算法在图像处理以及数据挖掘方面有相关的应用，其他领域的应用尚不成熟，甚至未涉及到水库调度方面。因此本文提出的改进猫群算法在水库调度方面的创新性探索有较重要的意义。

1 基于健康江湖关系的长江中游库群多目标调度模型

洞庭湖、鄱阳湖等是长江中游的国际重要湿地，在洪水调蓄、保护物种资源、维持生物多样性、污染降解和气候调节等方面具备无法代替的作用。然而，近年来，受到自然和人类活动的影响，湖的面积和体积持续缩减，水位持续下降，湿地面积萎缩严重，原有的湿地生物种群进化、时空分布方式被粉碎，出现陆地化进化趋势，不断出现生态环境问题，严重威胁湿地生态安全。综合考虑长江中游地区健康江湖关系的要求，以湖泊代表站的水位过程和水库的蓄水过程作为系统模型的优化目标，建立基于健康江湖关系的长江中游水库群多目标优化调度模型。长江中游水库群调度系统概化图如图1所示。

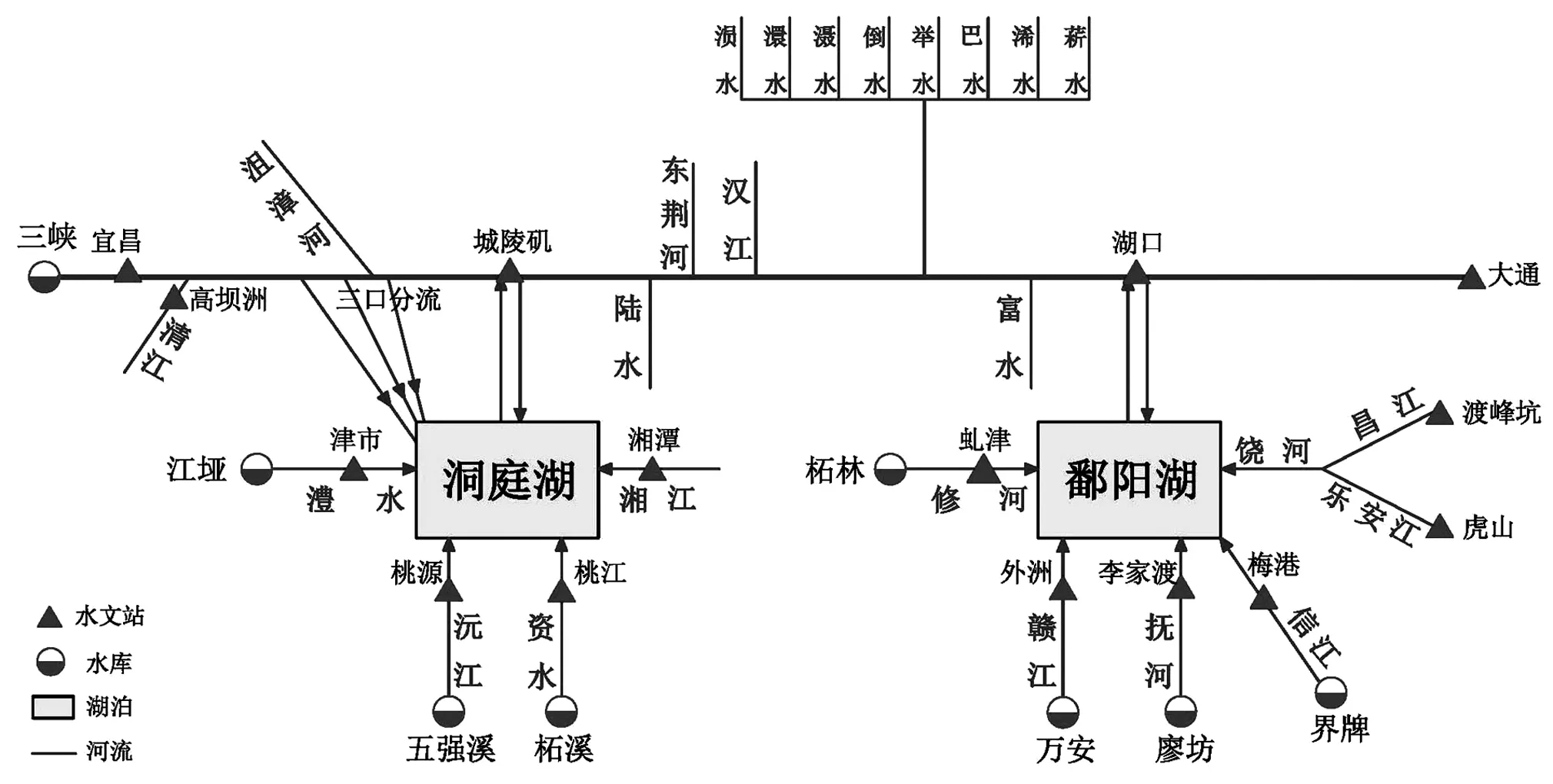
图1 长江中游水库群调度系统概化图Fig.1 Multi-reservoir system in middle reaehes of the Changjiang River

1.1 目标函数

主要考虑了洞庭湖和鄱阳湖健康目标，三峡水库、洞庭湖流域水库(江垭、五强溪及柘溪水库)和鄱阳湖流域水库(柘林、万安、廖坊及界牌水库)八座水库的蓄水目标。

(1)洞庭湖健康目标。通过洞庭湖代表站点的水位来评价洞庭湖的健康，以洞庭湖总健康度值最大为优化目标。其具体表达式如下：

(1)

式中：f11,t为洞庭湖代表站点第t个时段的湖泊健康度值。

(2)鄱阳湖健康目标。以鄱阳湖总健康度值最大为优化目标，其具体表达式如下：

(2)

式中：f12,t为鄱阳湖代表站点第t个时段的湖泊健康度值。

对于某个湖泊的某一代表站点，湖泊健康度的取值由站点单位时段的湖泊水位决定，表示为下式：

(3)

(3)水库蓄水目标。本文研究水库群蓄水期(10月和11月)的调度情况，为了满足水库的蓄水要求，以水库蓄水度最大作为水库蓄水的优化目标，使得水库尽量满足常规调度下的蓄水要求，以保证水库的正常运行。由于该模型中考虑的水库数目太多，故水库蓄水目标综合考虑了全部水库的蓄水目标，该目标函数的描述如下：

(4)

式中：k=1,2,3,…,8依次表示三峡水库，江垭水库，五强溪水库，柘溪水库，柘林水库，万安水库，廖坊水库，界牌水库。f2k,t表示第k水库t时段的蓄水目标值，其具体表达方式如下：

(5)

1.2 约束条件

(1)湖泊代表站水位约束：

hi,t,m≤hi,t≤i,t,n

(6)

(2)湖泊代表站流量约束：

QBi,t≤QBi,t,max

(7)

(3)水库蓄量约束：

Vk,t,min≤Vk,t≤Vk,t,max

(8)

(4)水库下泄能力约束：

Qk,t,min≤Qk,t≤Qk,t,max

(9)

(5)水量平衡约束：

Vk,t=Vi,t-1+(Ik,t-Qk,t)×Δtk,t

(10)

式中：hi,t,hi,t,m,hi,t,n分别为i湖泊代表站考虑湖泊健康的水位值、最低水位值和最高水位值；QBi,t,QBi,t,max分别为i湖泊代表站的流量值、安全流量值；Vk,t、Vk,t,min、Vk,t,max分别为k水库t时刻的蓄量、最低、最高蓄量约束，m3；Qk,t,min、Qk,t,max分别为k水库t时刻最小、最大下泄流量约束；Vk,t-1和Vk,t分别为k水库t时刻初末库容，m3；Ik,t和Qk,t分别为k水库时刻t的平均入库和下泄流量，m3/s；Δtk,t为k水库t时刻计算时间长度。

由于本研究中的通江湖泊水位受长江、四水、五河等来水的影响，对于一些特殊情况，采用传统的方法很难进行洪水演算。20世纪80年代初，长江委曾采用干流与湖泊连为一体的大湖演算方法，建立了长江中下游防洪系统的模拟模型[8]。本文依然采用大湖演算方法，演算时采用河段的槽蓄曲线和以水位日涨率、下游顶托、起涨水位等为参数的水位流量关系曲线[8,9]。

2 改进多目标猫群算法设计

猫群算法[10](Cat Swarm Optimization，CSO)于2006年由Shu-Chuan Chu提出的基于猫科动物行为的优化算法。猫的懒散休息且具有警惕性和发现目标后迅速捕捉猎物的两种模式分别称为搜寻模式和跟踪模式[11]。在猫群算法中，搜寻模式代表了寻优过程中的局部搜索，跟踪模式代表了寻优过程中的全局搜索，在迭代过程中将局部搜索和全局搜索相结合。猫群算法独特的搜索结构，使得它拥有克服遗传算法局部搜索能力不足和粒子群算法求解离散问题时容易陷入局部最优解的能力[10]。

传统的猫群优化算法通过固定的比例关系结合率(MR)将猫群分为跟踪模式和搜寻模式。在算法开始迭代阶段，算法的收敛速度较快，但随着迭代次数的增加，固定的MR会使有部分猫一直执行全局搜索，导致资源浪费。为解决这问题，本文采用改进的多目标猫群算法(IMCSO)，引入外部归档集来存储求解过程中的精英个体，并提出基于多目标优化的精英变异策略，以防止算法陷入局部解。

2.1 外部归档集构建及其规模维护

引入了精英个体保留机制，构造了进化种群之外的外部归档集 ELT()，其主要用来保留算法在求解过程中搜寻到的非支配解[12]。为使ELT()的规模得以维持并使其中的非劣解尽量分布均匀，本文采取一种“γ+1”的方式对ELT()规模进行维护，即每加入一个新个体都根据评价指标剔除一个指标最小的个体[13]。

设ELT()的规模为N，算法迭代次数为g。假设ELT(g-1)中存储着前(g-1)代种群进化中搜索到最优非劣解。对第g代种群中的每个个体(如j个个体 )进行以下操作：

(1)若ELT()为空集，则直接将ng,j放入ELT()中；

(2)如果ELT()不为空集，则将ng,j与ELT()中的个体进行Pareto比较。若ng,j不被ELT()中的所有个体支配，把ng,j加入ELT()中，同时删除ELT()中被支配的个体。

(3)如果ELT()的数目超过了最大数目N的限制，则删除ELT()中指标较小的个体，以维护ELT()中非劣解的均匀分布。

2.2 结合率改进

(11)

式中：MRt为迭代到第t代的结合率；t为迭代次数。可使算法在刚开始迭代时使用较大的结合率，可提高猫群的全局搜索能力。到迭代后期时，结合率较小，可使更大比例的猫能进行局部搜索，高效寻找非支配解。

2.3 基于多目标优化的精英变异策略

传统猫群算法可能出现“早熟”现象，为了使IMCSO恢复搜索能力，跳出局部最优，本文设计了一种适用于多目标优化的精英变异策略。对ELT()中的非劣解进行扰动，提升算法的优化性能。对ELT()中的任意个体etxi，搜索的具体过程如下：

⑴以个体etxi进行变异操作，得到新个体netxi；

netxi=etx1i+H(etx2i-etx3i)

(12)

式中：H为变异常数；etx1i，etx2i，etx3i是从外部归档集ELT()中任选的3个携带有最优前沿信息的精英个体，可使种群进化更有导向性，算法效率得到提升。

⑵比较个体etxi和新个体netxi的支配关系。若存在支配关系，则淘汰受支配个体，将非支配个体放入到ELT()中，并将其定义为个体etxi。若不存在支配关系，则直接将新个体netxi放入到ELT()中。

⑶若ELT()的规模超过了N，需对ELT()进行规模维护。

2.4 算法流程

IMCSO算法流程见图2。

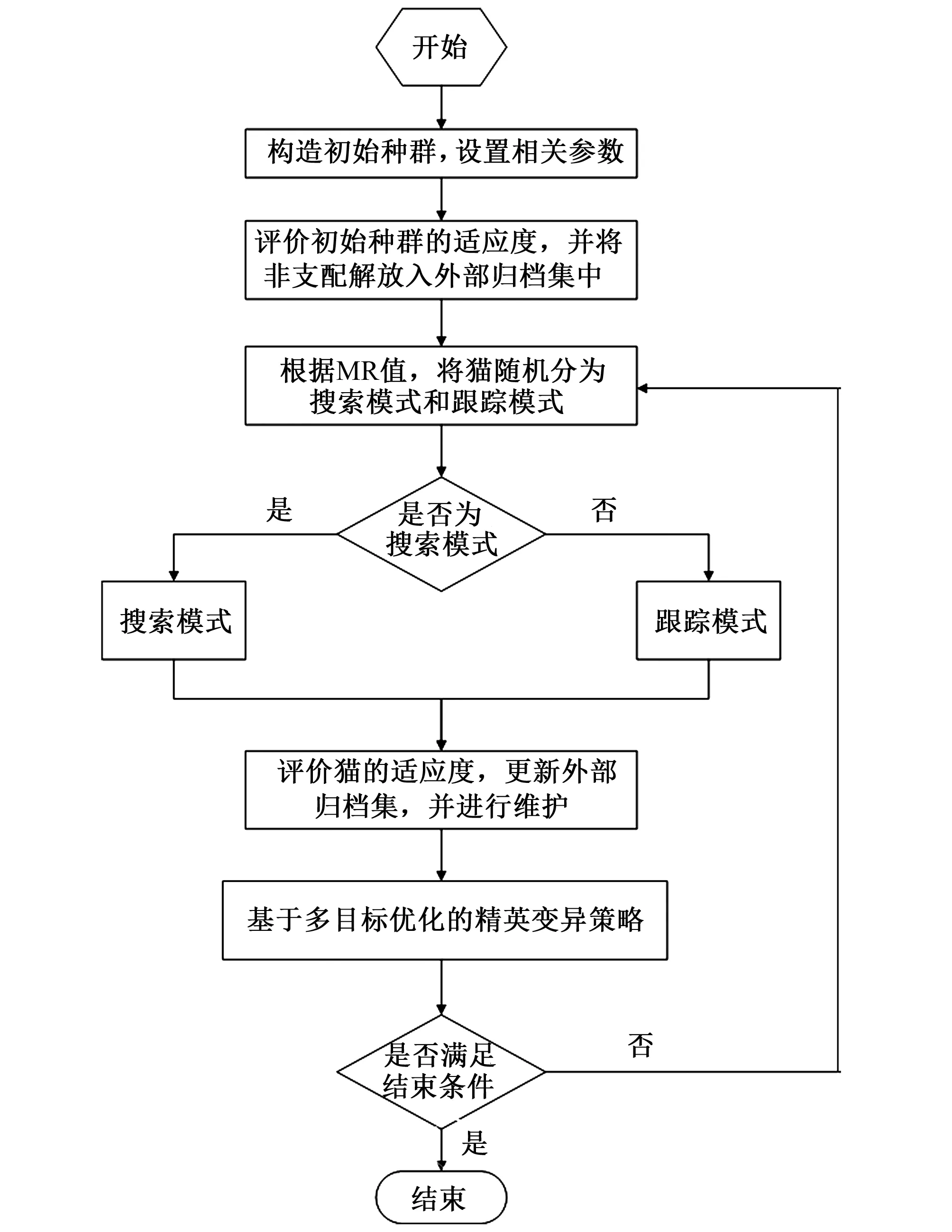
图2 IMCSO算法流程Fig.2 Flowchart for IMCSO algorithm

3 水库群多目标调度多目标决策

本文研究基于健康江湖关系的长江中游库群多目标调度，建模以水库蓄水度最大作为水库蓄水的优化目标，考虑的湖泊健康目标包括洞庭湖和鄱阳湖健康目标值尽可能大。

以水库群多目标调度决策优选的数据为基础构建决策矩阵，以不同调度偏好为指导，采用不同的调度过程可获得m个不同的调度方案集，A={Ai}，i=1,2,…,m。n个目标构成指标集，B={Bj}，j=1,2,…,n。方案Ai对目标Bj的属性值若为ui,j，则决策矩阵为：

(13)

进行水库群多目标调度的决策优选，首先由决策者基于不同的主观偏好作出评价，然后结合客观属性反映的信息以综合权重F=(fj),j=1,2,…,n的形式纳入到决策模型，最后根据排序函数选出综合理想程度最高的调度方案。

4 基于主观偏好和改进熵权的Vague集多属性决策方法

基于健康江湖关系的长江中游水库群多目标优化调度系统需从健康江湖关系的角度出发，在改善通江湖泊健康的前提下，尽可能确保水库蓄水期的正常蓄水，发挥健康江湖关系和水库经济效益的综合效益。由于湖泊健康目标与水库蓄水目标之间是相互竞争和冲突的关系，因此，有必要听取决策者和专家群体的意见，需要考虑在不同目标偏好情况下，对水库蓄泄过程进行合理安排，均衡协调各目标之间的利益以得到综合效益的充分发挥。但专家意见致使决策信息带有的主观性和不确定性较强，调度方案的制订还需考虑方案集自身所隐含的决策信息。

因此，为了使系统调度方案决策优选问题更加科学合理，本文采用主客观综合赋权法。考虑决策者的主观偏好，并结合熵权考虑研究对象的客观信息，以Vague集理论为基础，提出了一种基于主观偏好和改进熵权的Vague集多属性决策方法。

4.1 决策矩阵规范化

本文模型中均为效益型(越大越优)指标，需对决策方案进行规范化处理。

(14)

式中：xjmax，xjmin分别表示方案集中第j个指标的最大、最小值。

4.2 基于主观偏好的主观权重确定方法

依据专家的知识、经验和评价习惯，对指标可赋予不同类型的评价方式，如实数型、区间型以及语言型[14]。本文假设专家更偏好语言型评价，表1为用vague值表示的七级语言变量。假设第w位专家的权重为zw。

表1 用Vague值表示的七级语言变量Tab.1 The seven-level language variable representedby the Vague value

确定各偏好关系下的主观权重。

Step1：参照表1，将各专家的评价用Vague值语言变量来表示。

Step2：根据式(15)计算各偏好关系下的评价值的适合程度。参考刘华文[15]等人提出的方法，根据Vague值计算适合程度。

sdwj=twj+twj[1-twj-fwj]

(15)

式中：sdwj为在偏好关系d下，第w位专家(w=1,2,…,k)的评价对指标j的适合程度；twj和fwj为Vague集的一对隶属函数。

Step3：按照式(16)计算各偏好关系下，各位专家评价中各指标的主观权重。

(16)

Step4：按照式(17)计算各偏好关系下，各指标的主观权重。

(17)

4.3 基于改进熵权的客观权重确定方法

传统的熵权法中，当某一决策指标熵值Hj→1(j= 1,2,…,m)时, 熵值间存在的细微差别会导致属性熵权值差异的极度变大，文献[16]提出的改进熵权计算法在一定程度上解决了这一问题。但文献[16]提出的计算法，当Hj=1时，得到的熵权Yj>0。因此提出改进熵权法，熵权Yj改进计算公式具体如下：

(18)

4.4 多属性Vague集评估模型

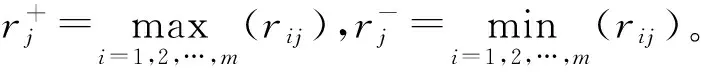
考虑到在实际决策问题中，决策方案在靠近正理想方案同时不一定与负理想方案远离。因此，通过综合考虑rij相对于r+j和r-j两方面的相对贴近程度来描述rij相对于理想方案的综合Vague真假隶属度，则rij相对理想方案的综合Vague真假隶属度[17]可通过如下公式计算：

(20)

其中，t+ij=tij×f-ij表示rij同时贴近r+j和远离r-j的程度；fij=f+ij×t-ij表示rij同时离开r+j和贴近r-j的程度。则rij相对于理想方案的综合Vague值矩阵为V=[tij,1-fij]m×n。

结合各评价指标的综合属性权重ω=[ω1,ω2,…,ωn]，可得到各候选决策方案相对于理想方案的综合Vague值为：

(22)

最后，依据各候选方案的综合Vague值计算各方案相对于理想方案的相符程度，用评分函数scorei=(S1(Xi),S2(Xi))来表示[18]，从而对各方案的优劣进行评价。提出新的排序函数，公式如下：

(23)

计算出各方案Vague值的S1(Xi)和S2(Xi)函数值，先比较S1(Xi)，S1(Xi)值越大，则方案i越优。当出现两个或两个以上方案的S1(Xi)值相同时，比较S2(Xi)，S2(Xi)大的方案更优。

4.5 基于主观偏好和改进熵权的Vague集多属性决策方法

step1：通过规范化处理，得到[0,1]范围内的相对优属度矩阵R=[ri,j]m×n。

step2：根据本文提出的方法确定各评价指标的客观权重Yi=(Y1,Y2,…,Yn)和主观权重Xj=(X1,X2,…,Xn)，最后综合主观权重Xi与客观权重Yj，获得所需要的属性综合权重ω=[ω1,ω2,…,ωn]，其中ωj=λXj+(1-λ)Yj。

step3：依据相对优属度矩阵R确定正理想方案为R+=(r+1,r+2,…,r+n)和负理想方案R-(r-1,r-2,…,r-n)，然后根据本文提出的方法得到各候选决策方案相对理想方案的综合Vague值，并运用式(23)对各方案进行优劣排序。

5 模型求解

5.1 算法编码方式

文献[2]分析得到洞庭湖区的最低生态水位为25 m，鄱阳湖区的生态水位区间为[14.29 m，14.65 m]。IMCSO算法的参数设置如下：种群大小为200，结合率最大值为0.6，结合率最小值为0.3，变异常数为0.2，外部归档集规模设为20，最大迭代次数设为200。选取长江中游1964年平水年历史径流资料作为预报来水及入库径流过程。

在运用IMCSO对调度模型进行求解时，采用各水库的水位作为算法的决策变量进行编码，则种群中第i个个体可表示为Ki={k1i,1,…,k1i,T；k2i,1,…,k2i,T；k3i,1,…,k3i,T；k4i,1,…,k4i,T；k5i,1,…,k5i,T；k6i,1,…,k6i,T；k7i,1,…,k7i,T；k8i,1,…,k8i,T}，其中k1i,t(t=1,2,…,T)表示三峡水库的蓄量过程；k2i,t(t=1,2,…,T)表示江垭水库的蓄量过程；k3i,t(t=1,2,…,T)表示五强溪水库的蓄量过程；k4i,t(t=1,2,…,T)表示柘溪水库的蓄量过程；k5i,t(t=1,2,…,T)表示柘林水库的蓄量过程；k6i,t(t=1,2,…,T)表示万安水库的蓄量过程；k7i,t(t=1,2,…,T)表示廖坊水库的蓄量过程；k8i,t(t=1,2,…,T)表示界牌水库的蓄量过程。调度期为10月和11月，时段长度为一日，时段数T=61。

5.2 多目标决策

假定参与决策过程的专家共有7位，假设7位专家的权重分别是0.154，0.214，0.172，0.103，0.107，0.047，0.203。决策分析中设置了侧重湖泊健康和侧重水库蓄水两种决策偏好，对于这两种不同的决策偏好，专家的评价结果见表2。

表2 不同决策偏好下各专家的语言型赋权结果Tab.2 The evaluation results of experts under differentdecision-making preferences

依据表2专家对指标作出的评价值，可求得侧重湖泊健康目标和侧重水库蓄水目标的主观权重向量分别为X1=(0.413，0.384，0.204)，X2=(0.197，0.163，0.640)。求得各个指标的熵值H=(0.977 6，0.944 2，0.910 9)，采用本文提出的改进熵权法求得各指标的熵权值为Y=(0.322，0.333，0.345)。取λ=0.5，侧重湖泊健康目标和侧重水库蓄水目标的综合权重向量分别为ω1=(0.367，0.358，0.275)，ω2=(0.260，0.248，0.492)。

5.3 调度结果及对比分析

1964年平水年来水条件下采用IMCSO求解得到的洞庭湖健康、鄱阳湖健康和水库蓄水的非劣调度方案集的目标值见表3。采用改进猫群算法(IMCSO)、猫群算法(CSO)和遗传算法(GA)求解得到的湖泊健康目标和水库蓄水目标的非劣调度方案集的空间分布如图3所示。

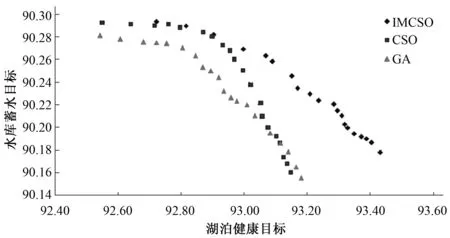
图3 非支配边界Fig.3 Nondominant boundary obtained by IMCSO algorithm

由图3可知，湖泊健康目标与水库蓄水目标之间存在一定的对立关系，研究分析的时段是在水库的蓄水期，在上游来水一定的情况下，若要满足水库蓄水要求则下泄的水量会相应减少，以致下游两湖代表站的水位下降，湖泊健康度降低。若要相应改善湖泊健康，需要保证湖泊代表站的水位，水库下泄要适当加大，水库蓄水要求得不到保证，所以湖泊健康目标与水库蓄水目标之间是相互竞争的关系，两者很难同时达到最优。图3比较了三种进化算法求解同一问题得到的非劣方案集，当考虑水库蓄水目标时，IMCSO求解出的最大目标值最大，略大于CSO的结果，GA得出的最大目标值最小。若考虑湖泊健康目标，GA寻优得出的最大目标值略大于CSO算法的结果，但经过改进后的猫群算法，可以在很大程度上提高目标值。多目标调度需均衡协调各目标之间的利益，在总体上IMCSO可以找到更加接近问题非支配边界的非劣解集，进一步体现了IMCSO的优异性能。

使用Vague集评估模型联合不同决策偏好下的综合权重得到各方案的Vague值并对其进行评分，具体结果见表4列出了依据评分函数值，并在表5中对方案集进行排序。

表4 方案集Vague评估结果Tab.4 The evaluation results of solution set

表5 方案集排序优选结果Tab.5 The optimization results of ranking alternatives

表5列出了方案集排序优选结果，从中可以看出，在侧重湖泊健康的情景下，此时方案优选会更加侧重湖泊健康目标。计算出的决策属性的综合权重为ω1=(0.367，0.358，0.275)，最优方案是湖泊健康总目标较大的方案(方案19)，最劣方案是湖泊健康总目标最小的方案(方案1)，方案的优劣排序结果与湖泊健康的变化情况基本一致。当决策过程侧重于水库蓄水时，决策属性的综合权重为ω2=(0.260，0.248，0.492)，此时对方案进行优选时会更侧重于水库蓄水目标。从表5的方案排序结果可以看出，这种决策偏好下出现了水库蓄水目标较大的方案(方案3)最优，水库蓄水目标最小的方案(方案20)最劣，决策方案优选排序结果与水库蓄水目标的变化大体一致。

为了进一步分析不同调度方案间的差异，选取了表3中3个典型非劣调度方案(方案1、方案10和方案20)，列出了洞庭湖代表站城陵矶和鄱阳湖代表站湖口的水位过程及三峡水库的蓄水过程进行对比分析，见图4、图5及图6。

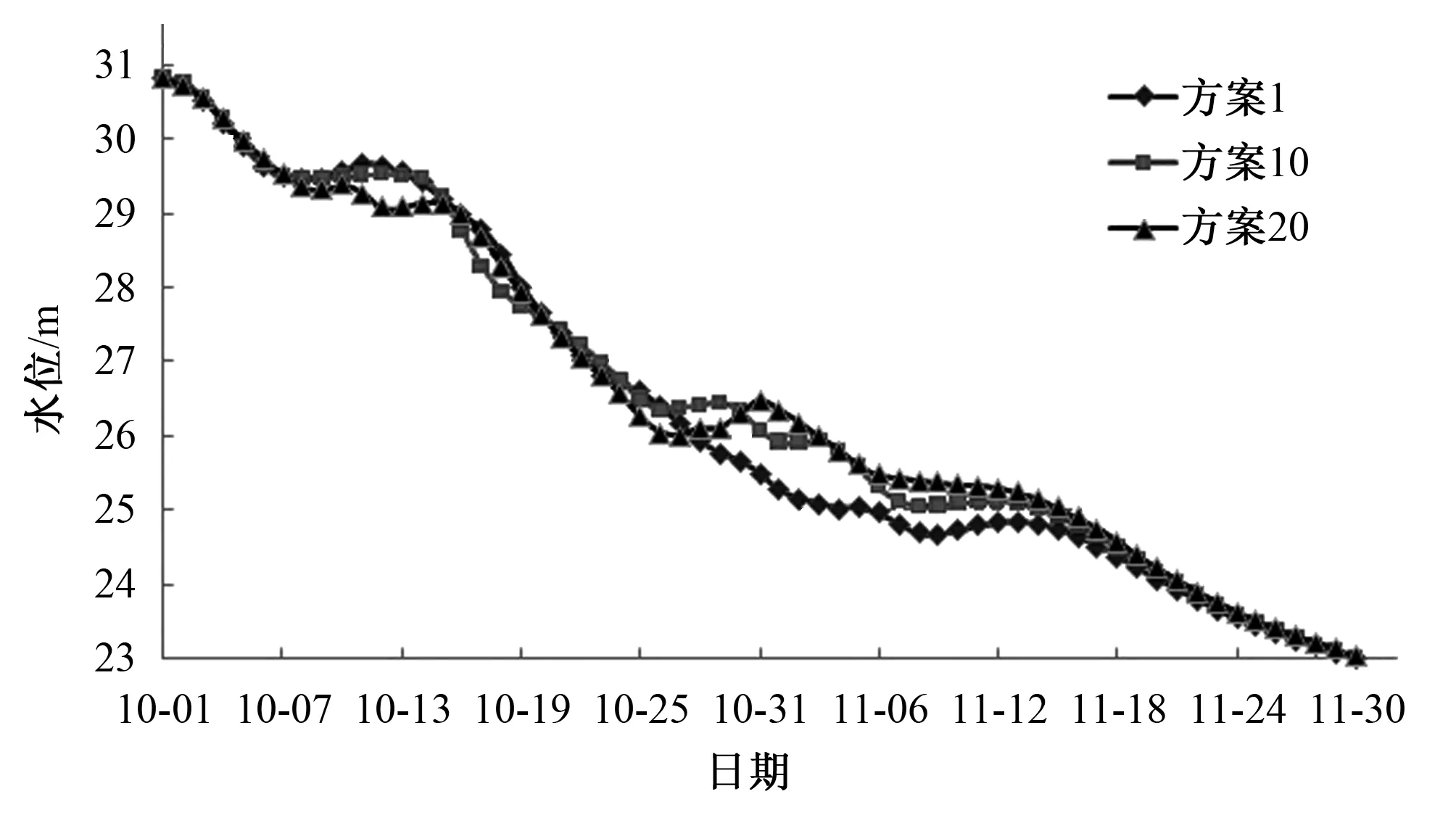
图4 1964年历史来水条件下的洞庭湖-城陵矶水位过程Fig.4 The water level of Dongting lake-Chenglingji in 1964

图5 1964年历史来水条件下的鄱阳湖-湖口水位过程Fig.5 The water level of Poyang lake-Hukou in 1964

由图4及5可以看出，各调度方案城陵矶和湖口水位过程方案1要稍低于方案10，方案10要稍低于方案20。方案20更侧重于湖泊健康，在水库蓄水期加大了水库下泄水量，达到湖泊健康度最大化的目的。与方案20相比，方案1和方案20的调度模式均不同程度的考虑了水库蓄水需求，在水库蓄水期降低了水库下泄流量，但这一措施不可避免地使湖泊代表站水位降低，进而影响湖泊健康状况。

图6 1964年历史来水条件下的三峡水位过程Fig.6 The water level of Sanxia in 1964

由图6可以发现，方案1、方案10及方案20的水库蓄满时间基本要迟于规划设计的蓄满时间，且各水库的蓄满时间基本是方案20最迟。各方案都有不同程度的考虑了洞庭湖和鄱阳湖的健康需求，在多目标竞争中，湖泊健康目标值的提升必然会以水库蓄水目标值的下降为代价。同时方案20对于湖泊健康目标的侧重程度更高，水库在蓄水过程中会加大下泄水量，水库储存的水量减少，必然导致水库的蓄量偏低。

6 结论与展望

(1)本文研究长江中游水库水利工程建设与运行下对江湖关系的影响，建立了基于健康江湖关系的多目标优化调度模型，得到不同偏好下的水库群联合调度方案，对缓解两湖地区生态恶化、构建生态友好型社会具有重要的理论指导意义。

(2)针对猫群算法存在的问题，提出了改进的多目标猫群算法求解水库群多目标调度问题。通过IMCSO算法对模型进行高效求解，得到不同偏好下的水库群联合调度方案。

(3)提出了一种适用于系统方案优选的基于主观偏好和改进熵权的Vague集多属性决策方法，并将该多属性决策方法运用于长江中游水库群多目标优化调度方案决策优选问题研究，确定了不同决策偏好下方案的优劣排序。

(4)长江中游水文情势较为复杂，本文建立的多目标优化调度模型只考虑了洞庭湖健康、鄱阳湖健康和水库蓄水3个目标，而涉及的水库防洪、发电、供水等目标却未进行考虑。在蓄水期，长江流域水库的蓄水是导致通江湖泊水位偏低的一个重要原因，因此本文只初步分析了蓄水期，在后续研究中需考虑枯水期水库群的调度情况，实现流域蓄水期、枯水期的连续性调度。

□

[1] 李 倩. 三峡工程对洞庭湖生态环境的影响[D].长沙:湖南大学, 2005.

[2] 康 婧.三峡工程对两湖地区的生态补偿技术研究[D].天津:天津大学, 2011.

[3] 刘 影, 徐 燕. 三峡工程对鄱阳湖候鸟保护区的影响及对策探讨[J]. 江西师范大学学报(自然科学版),1994,18(4):375-380.

[4] Yuhui Shi, Russell C.Eberhart. Empirical study of particle swarm optimization[C]∥ Proceeding of Congress on Evolutionary Computing. Piscataway, NJ: IEEE Service Center, 1999:1 945-1 950.

[5] Shu-chuan Chu, Pei-wei Tsai. Computational intelligence based on the behavior of cats[J].International Journal of Innovative Computing, Information and Control, 2007,3(1):163-173.

[6] Pei-Wei Tsai, Jeng-Shyang Pan, Bin-Yih Liao, et al. Enhanced artificial bee colony optimization[J]. Information Journal of Innovative Computing, Information and Control, 2009,5(12):5 081-5 092.

[7] Pradhan Pyari Mohan, Panda Ganapati. Solving multiobjective problems using cats warm optimization[J].Expert Systems with Applications, 2012,39(3):2 956-2 964.

[8] 刘文标. 三峡水库运行初期对鄱阳湖汛期高水位变化趋势的影响研究[D]. 南昌:南昌大学, 2007.

[9] 宁 磊.长江中游江湖关系与防洪形势研究[D].武汉:武汉大学,2010.

[10] Shu-chuan Chu, Pei-wei Tsai, Jeng-shyang Pan. Cat swarm optimization[C]∥ 9th Pacific Rim International Conference on Artificial Intelligence. Berlin Germany: Springer Verlag, 2006:854-858.

[11] 范正伟,刘 琼, 李新鹏. 多目标猫群算法求解切削参数优化问题[J]. 软件导刊,2013,12(3):116-118.

[12] 郑金华. 多目标进化算法及其应用[M]. 北京: 科学出版社, 2007.

[13] 卢有鳞. 流域梯级大规模水电站群多目标优化调度与多属性决策研究[D]. 武汉：华中科技大学, 2012.

[14] 翟伟静.工程机械类融资租赁的信用风险管理研究[D].重庆:重庆大学,2011.

[15] 刘华文.多目标模糊决策的Vague集方法[J]. 系统工程理论与实践, 2004,(5):103-109.

[16] 周惠成,张改红,王国利. 基于熵权的水库防洪调度多目标决策方法及应用[J].水利学报, 2007,38(1):100-106.

[17] 李英海.梯级水电站群联合优化调度及其决策方法[D]. 武汉：华中科技大学,2009.

[18] 李英海, 周建中. 基于改进熵权和Vague集的多目标防洪调度决策方法[J]. 水电能源科学, 2010,28(6):32-35.